5.1: Angles
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Draw angles in standard position.
- Convert between degrees and radians.
- Find coterminal angles.
Angles
In this section, we will examine properties of angles.
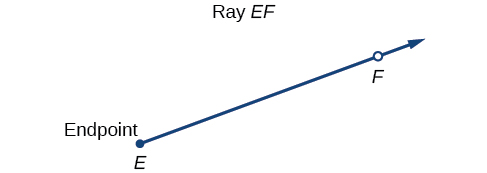
Properly defining an angle first requires that we define a ray. A ray consists of one point on a line and all points extending in one direction from that point. The first point is called the endpoint of the ray. We can refer to a specific ray by stating its endpoint and any other point on it. The ray illustrated in the figure to the right can be named as ray EF, or in symbolic form →EF.
the union of two rays with a common endpoint
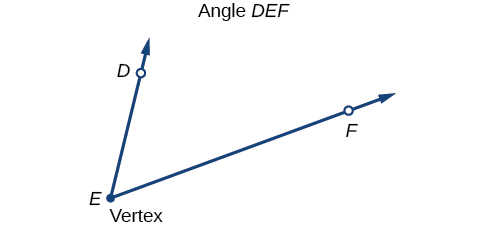
An angle is the union of two rays having a common endpoint as shown in Figure 5.1.2. The endpoint is called the vertex of the angle, and the two rays are the sides of the angle. The angle illustrated in the figure on the right is formed from rays →ED and →EF. Angles can be named using a point on each ray and the vertex, such as angle DEF, or in symbolic form ∠DEF.
Greek letters are often used as variables for the measure of an angle. In the table below is a list of Greek letters commonly used to represent angles.
| θ | φ or ϕ | α | β | γ |
| theta | phi | alpha | beta | gamma |
amount rotation that separates the two rays of an angle
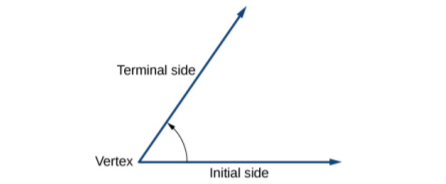
Angle creation is a dynamic process. We start with two rays lying on top of one another. We leave one fixed in place, and rotate the other. The fixed ray is the initial side, and the rotated ray is the terminal side. In order to identify the different sides, we indicate the rotation with a small arc and arrow close to the vertex as in Figure 5.1.3.
When applications use angles, we must be able to measure them.
Definition: Measurement of an angle
The measure of an angle indicates the amount of rotation from the initial side to the terminal side.
The measure of an angle is positive when the angle is measured in a counterclockwise direction from the initial side to the terminal side.
The measure of an angle is negative when the angle is measured in a clockwise direction from the initial side to the terminal side.
Degrees
Probably the most familiar unit of angle measurement is the degree. One degree is 1360 of a circular rotation, so a complete circular rotation contains 360 degrees. An angle measured in degrees should always include the unit “degrees” after the number, or include the degree symbol °. For example, 90 degrees = 90°.
To formalize our work, we will begin by drawing angles on an x-y coordinate plane. Angles can occur in any position on the coordinate plane, but for the purpose of comparison, the convention is to illustrate them in the same position whenever possible.
Definition: Standard Position
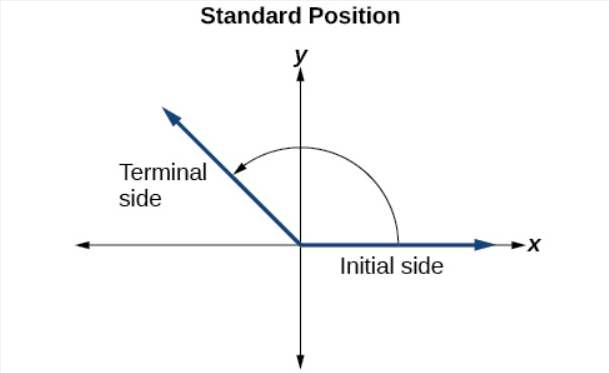
An angle is in standard position if its vertex is located at the origin, and its initial side extends along the positive x-axis. See Figure 5.1.5.
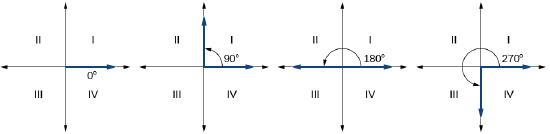
Angles in standard position are classified according to where their terminal side lies. For instance, an angle in standard position whose terminal side lies in Quadrant I is called a `Quadrant I angle' or 'an angle in Quadrant I'. If the terminal side of an angle lies on one of the coordinate axes, it is called a quadrantal angle. Two angles in standard position are called coterminal if they share the same terminal side.
Drawing an angle in standard position always starts the same way—draw the initial side along the positive x-axis.
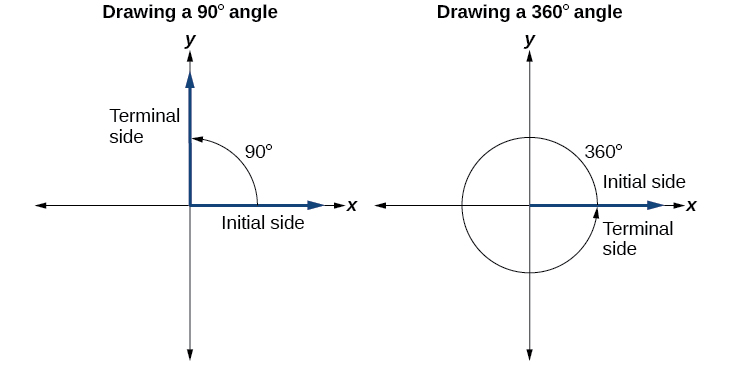
To place the terminal side of the angle, we must calculate the fraction of a full rotation the angle represents. We do that by dividing the angle measure in degrees by 360°. For example, to draw a 90° angle, we calculate that \frac{90°}{360°}=\frac{1}{4}. So, the terminal side will be one-fourth of the way around the circle, moving counterclockwise from the positive x-axis. To draw a 360° angle, we calculate that \frac{360°}{360°}=1. So the terminal side will be 1 complete rotation around the circle, moving counterclockwise from the positive x-axis. In this case, the initial side and the terminal side overlap. See Figure \PageIndex{6} .
Since we define an angle in standard position by its initial side, we have a special type of angle whose terminal side lies on an axis.
Definition: QUADRANTAL ANGLES
Quadrantal angles are angles in standard position whose terminal side lies on an axis.
Examples of quadrantal angles include 0°, 90°, 180°, 270°, or 360°.
![]() Howto: Draw an angle in standard position, given an angle measure in degrees.
Howto: Draw an angle in standard position, given an angle measure in degrees.
- Express the angle measure as a fraction of 360°.
- Reduce the fraction to simplest form.
- Draw an angle that contains that same fraction of the circle, beginning on the positive x-axis and moving counterclockwise for positive angles and clockwise for negative angles.
Example \PageIndex{1}: Drawing an Angle in Standard Position Measured in Degrees
- Sketch an angle of 30° in standard position.
- Sketch an angle of −135° in standard position.
Solution
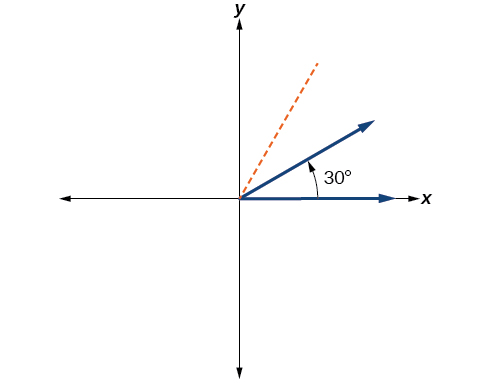 Divide the angle measure by 360°.
Divide the angle measure by 360°.
\dfrac{30°}{360°}=\dfrac{1}{12}
To rewrite the fraction in a more familiar fraction, we can recognize that
\dfrac{1}{12}=\dfrac{1}{3}\left(\dfrac{1}{4}\right)
One-twelfth equals one-third of a quarter, so by dividing a quarter rotation into thirds, we can sketch a line at 30° as shown in the figure to the right.
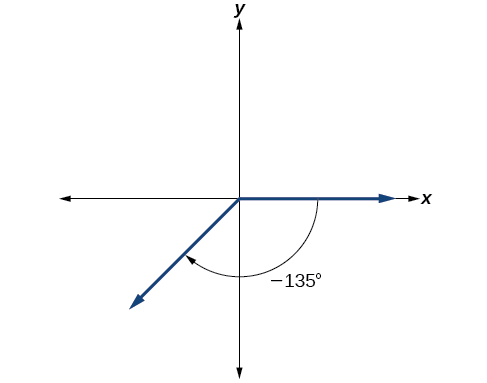 Divide the angle measure by 360°.
Divide the angle measure by 360°.
\dfrac{−135°}{360°}=−\dfrac{3}{8}
In this case, we can recognize that
−\dfrac{3}{8}=−\dfrac{3}{2}\left(\dfrac{1}{4}\right)
Negative three-eighths is one and one-half times a quarter, so we place a line by moving clockwise one full quarter and one-half of another quarter, as in the figure to the right.
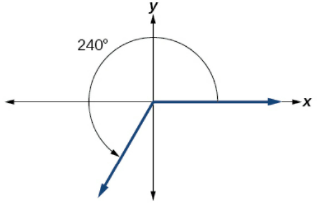
![]() Try It \PageIndex{1}
Try It \PageIndex{1}
Show an angle of 240° on a circle in standard position.
- Answer
Radians
Dividing a circle into 360 parts is an arbitrary choice, although it creates the familiar degree measurement. We may choose other ways to divide a circle. To find another unit, think of the process of drawing a circle. Imagine that you stop before the circle is completed. The portion that you drew is referred to as an arc. An arc may be a portion of a full circle, a full circle, or more than a full circle, represented by more than one full rotation. The length of the arc around an entire circle is called the circumference of that circle.
In the previous example we illustrated a method of drawing an angle by determining the fraction of the measure of an angle to the measure of a full rotation. This is the same as the fraction of the arclength of an angle to 2πr, the arclength of a complete rotation (i.e. the circumference) of a circle. Building on this idea, we define a new way to measure an angle, as the fraction of the arclength of an angle to the radius of a circle, which is just 2π times the fraction used when drawing an angle.
Definition: Radian Measure
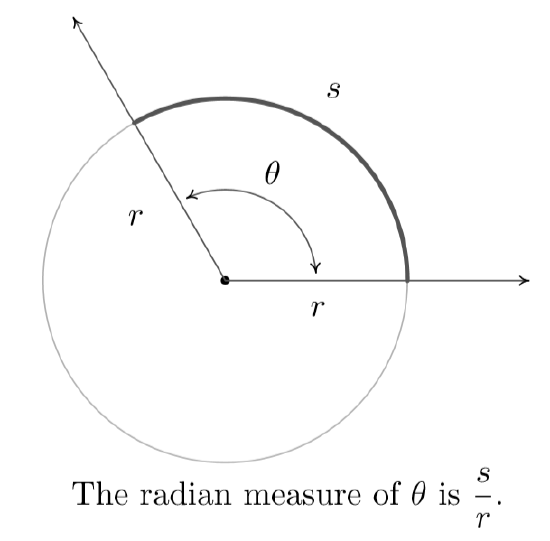 The radian measure of an angle is the ratio of an arc measuring s units to the radius r of the circle containing this arc.
The radian measure of an angle is the ratio of an arc measuring s units to the radius r of the circle containing this arc.
The measure of the angle in radians is the ratio \dfrac{s}{r} .
The radian measure of an angle \theta is the number of 'radius lengths' needed to sweep out along the circle to subtend the angle \theta.
One complete revolution measures 2π radians.
Note that when an angle is described without a specific unit, it refers to radian measure.
Radian measure is dimensionless, since it is the quotient of a length (portion of a circumference) divided by a length (radius) and the length units cancel out. Therefore, it is not necessary to write the label “radians” after a radian measure, and if we see an angle that is not labeled with “degrees” or the degree symbol, we can assume that it is a radian measure. In contrast, if the angle is measured in degrees, the units must be specified.
Radian measure is the number of radii in the length of an arc of a circle
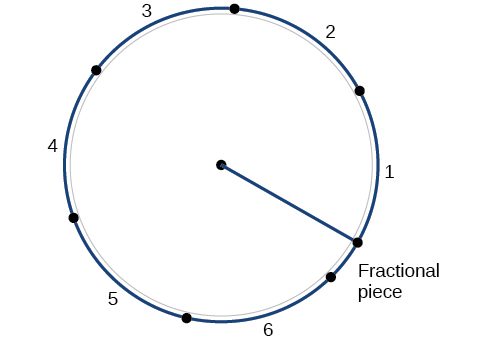 One full rotation has an arc length equal to the circumference of a circle. The circumference of a circle is C=2πr. The angle measure of one complete rotation in radian measure is \dfrac{2πr}{r}, which is always 2π≈6.28, regardless of the length of the radius. So the circumference of any circle is 2π≈6.28 times the length of the radius. That means that if we took a string as long as the radius and used it to measure consecutive lengths around the circumference, there would be room for six full string-lengths and a little more than a quarter of a seventh, as shown in the figure on the right.
One full rotation has an arc length equal to the circumference of a circle. The circumference of a circle is C=2πr. The angle measure of one complete rotation in radian measure is \dfrac{2πr}{r}, which is always 2π≈6.28, regardless of the length of the radius. So the circumference of any circle is 2π≈6.28 times the length of the radius. That means that if we took a string as long as the radius and used it to measure consecutive lengths around the circumference, there would be room for six full string-lengths and a little more than a quarter of a seventh, as shown in the figure on the right.
This brings us to our new angle measure.
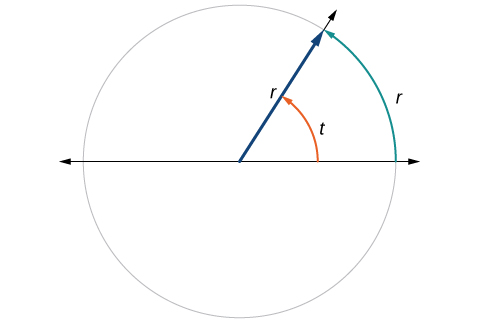
One radian is the measure of a central angle of a circle that intercepts an arc equal in length to the radius of that circle. A central angle is an angle formed at the center of a circle by two radii. Because the total circumference equals 2π times the radius, a full circular rotation is 2π radians. So
\begin{align*} 2π \text{ radians } & =360^∘ && \text{one complete rotation}\\ π \text{ radians } & =\dfrac{360^∘}{2}=180^∘ && \text{one-half of a complete rotation}\\ 1 \text{ radian } & =\dfrac{180^∘}{π}≈57.3^∘ \end{align*}
The measure of one radian is depicted in Figure \PageIndex{12}. The angle t sweeps out a measure of one radian. Notice that the length of the intercepted arc is the same as the length of the radius of the circle.
Radian measure is independent of the radius of the circle containing the arc
The ratio of the length of the curve along the arc of a circle to the radius of the circle containing that arc is the radian measure of the angle. This ratio is the same regardless of the radius of the circle—it depends only on the angle. This property allows us to define a measure of any angle as the ratio of the arc length s to the radius r.
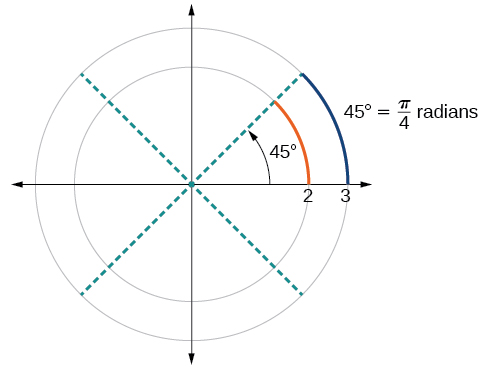 To elaborate on this idea, consider two circles, one with radius 2 and the other with radius 3. Recall the circumference of a circle is C=2πr, where r is the radius. The smaller circle then has circumference 2π(2)=4π and the larger has circumference 2π(3)=6π. Now we draw a 45° angle on the two circles, as in the figure on the right. The length of the arc subtended by 45^{\circ} is one-eighth of the circumference because 45^{\circ} is one-eighth of a complete rotation. So the length of the arc subtended by 45^{\circ} for the circle of radius 2 is \tfrac{1}{8}4π = \frac{1}{2}π and the length of the arc subtended by 45^{\circ} for the circle of radius 3 is \tfrac{1}{8}6π = \frac{3}{4}π.
To elaborate on this idea, consider two circles, one with radius 2 and the other with radius 3. Recall the circumference of a circle is C=2πr, where r is the radius. The smaller circle then has circumference 2π(2)=4π and the larger has circumference 2π(3)=6π. Now we draw a 45° angle on the two circles, as in the figure on the right. The length of the arc subtended by 45^{\circ} is one-eighth of the circumference because 45^{\circ} is one-eighth of a complete rotation. So the length of the arc subtended by 45^{\circ} for the circle of radius 2 is \tfrac{1}{8}4π = \frac{1}{2}π and the length of the arc subtended by 45^{\circ} for the circle of radius 3 is \tfrac{1}{8}6π = \frac{3}{4}π.
Notice what happens if we find the ratio of the arc length divided by the radius of the circle.
\begin{align*} \text{Smaller circle: } \dfrac{\frac{1}{2}π}{2} & =\dfrac{1}{4}π \qquad \qquad \text{Larger circle: } \dfrac{\frac{3}{4}π}{3} & =\dfrac{1}{4}π \end{align*}
Since both ratios are \frac{1}{4}π, the angle measures of both circles are the same, even though the arc lengths and radii differ.
Example \PageIndex{2}: Finding a Radian Measure
Find the radian measure of one-third of a full rotation.
Solution
For any circle, the arc length along such a rotation would be one-third of the circumference. The circumference is 2πr so the arc length s is
\begin{align*}s &= \dfrac{1}{3}(2πr) =\dfrac{2πr}{3} \nonumber \end{align*}
The radian measure would be the arc length divided by the radius.
\begin{align*} \text{radian measure} & = \dfrac{\frac{2πr}{3}}{r} = \dfrac{2πr}{3r} = \dfrac{2π}{3} \nonumber \end{align*}
![]() Try It \PageIndex{2}
Try It \PageIndex{2}
Find the radian measure of three-fourths of a full rotation.
- Answer
- \dfrac{3π}{2}
Special Angles
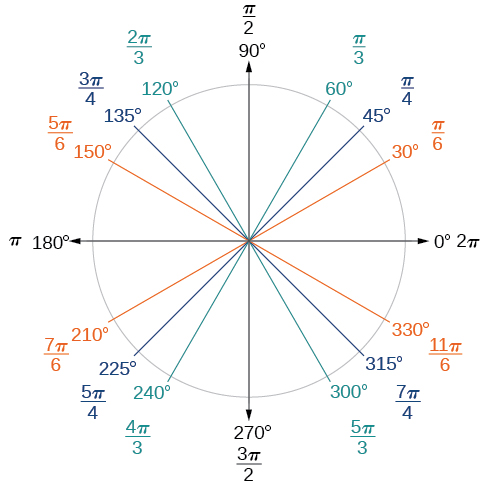 There are some frequently encountered angles in one revolution of a circle with which we should be familiar. The figure on the right illustrates these commonly encountered angles measured in radians and degrees. These angles include basic angles that have their terminal side in Quadrant I or along the positive axes, and multiples of these basic angles that have their terminal side in the other quadrants. Notice that angles drawn in the same color are multiples of the same basic angle.
There are some frequently encountered angles in one revolution of a circle with which we should be familiar. The figure on the right illustrates these commonly encountered angles measured in radians and degrees. These angles include basic angles that have their terminal side in Quadrant I or along the positive axes, and multiples of these basic angles that have their terminal side in the other quadrants. Notice that angles drawn in the same color are multiples of the same basic angle.
The basic angles are 0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}, and 90^{\circ} and their radian measure equivalents, 0, \frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}, and \frac{\pi}{2}.
The other angles can be obtained from the basic angle \theta by performing simple addition or subtraction.
\begin{align*} &\text{Angles in Quadrant II: }\quad && 180^{\circ} - \theta \text{ (in degrees)} && = π - \theta \text{ (in radians)}\\[2mm] &\text{Angles in Quadrant III: } && 180^{\circ} + \theta \text{ (in degrees)} && = π + \theta \text{ (in radians)}\\[2mm] &\text{Angles in Quadrant IV: } && 360^{\circ} - \theta \text{ (in degrees)} && = 2π - \theta \text{ (in radians)} &\end{align*} .
The basic angles in Quadrant I are examples of reference angles. We will see shortly that reference angles play an important role in the evaluation of trigonometric ratios.
Converting Between Radians and Degrees
Because degrees and radians both measure angles, we need to be able to convert between them. However, while converting back and forth between degrees and radians is certainly a good skill to have, it is best that you learn to `think in radians' as well as you can `think in degrees'.
Since one revolution counter-clockwise measures 360^{\circ} and the same angle measures 2 \pi radians, we can use the proportion \frac{2 \pi \, \text{radians}}{360^{\circ}}, or its reduced equivalent, \frac{\pi \, \text{radians}}{180^{\circ}}, as the conversion factor between the two systems. A proportion equation can be set up to do the conversion, or cancellation of units can be done.
We summarize these conversions below.
![]() Howto: Convert between Degrees and Radians.
Howto: Convert between Degrees and Radians.
- To convert degree measure to radian measure, multiply by \dfrac{\pi \, \text{radians}}{180^{\circ}} \\[2mm]
- To convert radian measure to degree measure, multiply by \dfrac{180^{\circ}}{\pi \, \text{radians}}
~or~ Solve the proportion equation \dfrac{θ \text{ (in degrees)}}{180^{\circ}}=\dfrac{θ \text{ (in radians)}}{π \text{ radians} }
Example \PageIndex{3}: Converting Radians to Degrees
Convert each radian measure to degrees. 1) 3 2) \dfrac{π}{6}
Solution
- Cancellation of Units Method. Use the appropriate equivalency ratio, \dfrac{180^{\circ}}{\pi \, \text{radians}} .
\theta = 3 \text{ radians} \cdot \dfrac{180^{\circ}}{π \text{ radians} } = 3 {\cancel{\text{ radians}}} \cdot \dfrac{180^{\circ}}{π {\cancel{\text{ radians}}} } = \dfrac{3(180)^∘}{π} ≈172^∘
- Proportion Method. Use the proportion equation \dfrac{θ \text{ (in degrees)}}{180^{\circ}} =\dfrac{θ \text{ (in radians)}}{π \text{ radians} } then substitute.
\begin{align*} \dfrac{θ}{180^{\circ}} & =\dfrac{\frac{π}{6}}{π} \\ θ & =180 \left( \dfrac{π}{6} \cdot \dfrac{1}{π} \right) =\dfrac{180^{\circ}}{6} =30^∘ \nonumber \end{align*}
![]() Try It: \PageIndex{3}
Try It: \PageIndex{3}
Convert −\frac{3π}{4} radians to degrees.
Solution
−135°
Example \PageIndex{4}: Converting Degrees to Radians
- Convert 127^{\circ} to radians. Write the answer to the nearest tenth of a radian.
- Convert 15 degrees to radians. Write the answer in units of \pi
Solution
1. Cancellation of Units Method. Use the appropriate equivalency ratio, \dfrac{\pi \, \text{radians}}{180^{\circ}}
\begin{align*} \theta &= 127^{\circ} \cdot \dfrac{\pi \text{ radians}}{180^{\circ}} \\[2mm] &= 127^{\cancel{\circ}} \cdot \dfrac{\pi \text{ radians}}{180^{\cancel{\circ}}} \\ &= \dfrac{127(\pi) \text{ radians}}{180} ≈2.2 \text{ radians} \nonumber \end{align*}
2. Proportion Method. In this example, we start with degrees and want radians, so we again set up a proportion and solve it, but we substitute the given information into a different part of the proportion.
\begin{align*} \dfrac{θ \text{ (in degrees)}}{180^{\circ}} &=\dfrac{θ \text{ (in radians)}}{π \text{ radians} } \\[2mm] \dfrac{15^{\circ}}{180^{\circ}} &=\dfrac{ \theta }{π \text{ radians} } \\ π \left( \dfrac{15^{\circ}}{180^{\circ}} \right) &=π \left( \dfrac{ \theta }{π \text{ radians} } \right) \\ \dfrac{15π \text{ radians}}{180} & =θ \\ \dfrac{π}{12}\text{ radians} & =θ \nonumber \end{align*}
![]() Try It: \PageIndex{4}
Try It: \PageIndex{4}
Convert 126° to radians written as a multiple of \pi.
Solution
\frac{7π}{10}
Coterminal Angles
Negative angles and angles greater than a full revolution are often more awkward to work with than those in the range of 0° to 360°, or 0 to 2π. It would be convenient to replace those out-of-range angles with a corresponding angle within the range of a single revolution.
Definition: Coterminal Angles
Coterminal angles are angles in standard position that have the same terminal side.
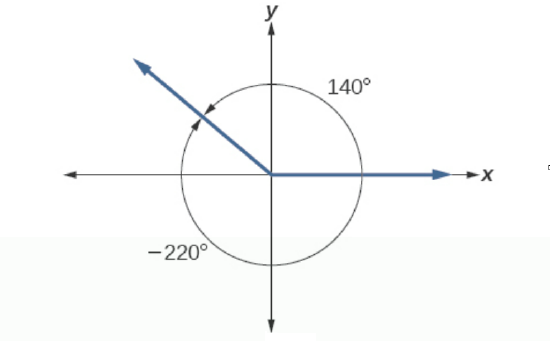 It is possible for more than one angle to have the same terminal side. Look at the figure on the right for an example. The angle of 140° is a positive angle, measured counterclockwise. The angle of –220° is a negative angle, measured clockwise. Because both angles have the same terminal side, they are coterminal angles. Every angle greater than 360° or less than 0° is coterminal with an angle between 0° and 360°, and it is often more convenient to find the coterminal angle within the range of 0° to 360° than to work with an angle that is outside that range.
It is possible for more than one angle to have the same terminal side. Look at the figure on the right for an example. The angle of 140° is a positive angle, measured counterclockwise. The angle of –220° is a negative angle, measured clockwise. Because both angles have the same terminal side, they are coterminal angles. Every angle greater than 360° or less than 0° is coterminal with an angle between 0° and 360°, and it is often more convenient to find the coterminal angle within the range of 0° to 360° than to work with an angle that is outside that range.
Any angle has infinitely many coterminal angles because each time we add 360° to that angle—or subtract 360° from it—the resulting value has a terminal side in the same location. For example, 100° and 460° are coterminal for this reason, as is −260°. Recognizing that any angle has infinitely many coterminal angles explains the repetitive shape in the graphs of trigonometric functions.
![]() How to: Find a Coterminal Angle.
How to: Find a Coterminal Angle.
Given an angle \theta measured in degrees, any angle calculated by increasing or decreasing \theta by a multiple of 360^{\circ} is coterminal to \theta.
Given an angle \theta measured in radians, any angle calculated by increasing or decreasing \theta by a multiple of 2\pi radians is coterminal to \theta.
Example \PageIndex{5}: Find an Angle Coterminal with an Angle Measured in Degrees
- Find the least positive angle θ that is coterminal with an angle measuring 800°, where 0°≤θ<360°.
- Show the angle with measure −45° on a circle and find a positive coterminal angle α such that 0° ≤ α < 360°.
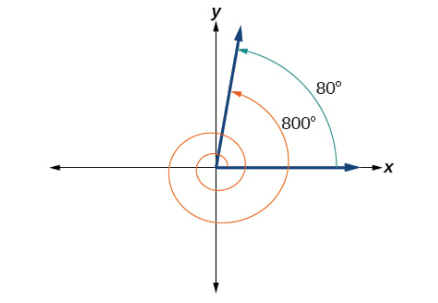
1. Solution
An angle with measure 800° is coterminal with an angle with measure 800° − 360° = 440°, but 440° is still greater than 360°, so we subtract 360° again to find another coterminal angle: 440° − 360° = 80°.
The angle θ=80° is coterminal with 800°. To put it another way, 800° equals 80° plus two full rotations, as shown in Figure \PageIndex{19}.
2. Solution
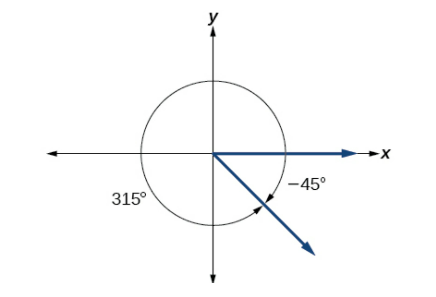
Since 45° is half of 90°, we can start at the positive horizontal axis and measure clockwise half of a 90° angle.
Because we can find coterminal angles by adding or subtracting a full rotation of 360°, we can find a positive coterminal angle here by adding 360°:
−45°+360°=315° so the angle 315° is coterminal with -45°.
These two coterminal angles are drawn below in Figure \PageIndex{20}.
Example \PageIndex{5b}: Coterminal angles in degrees
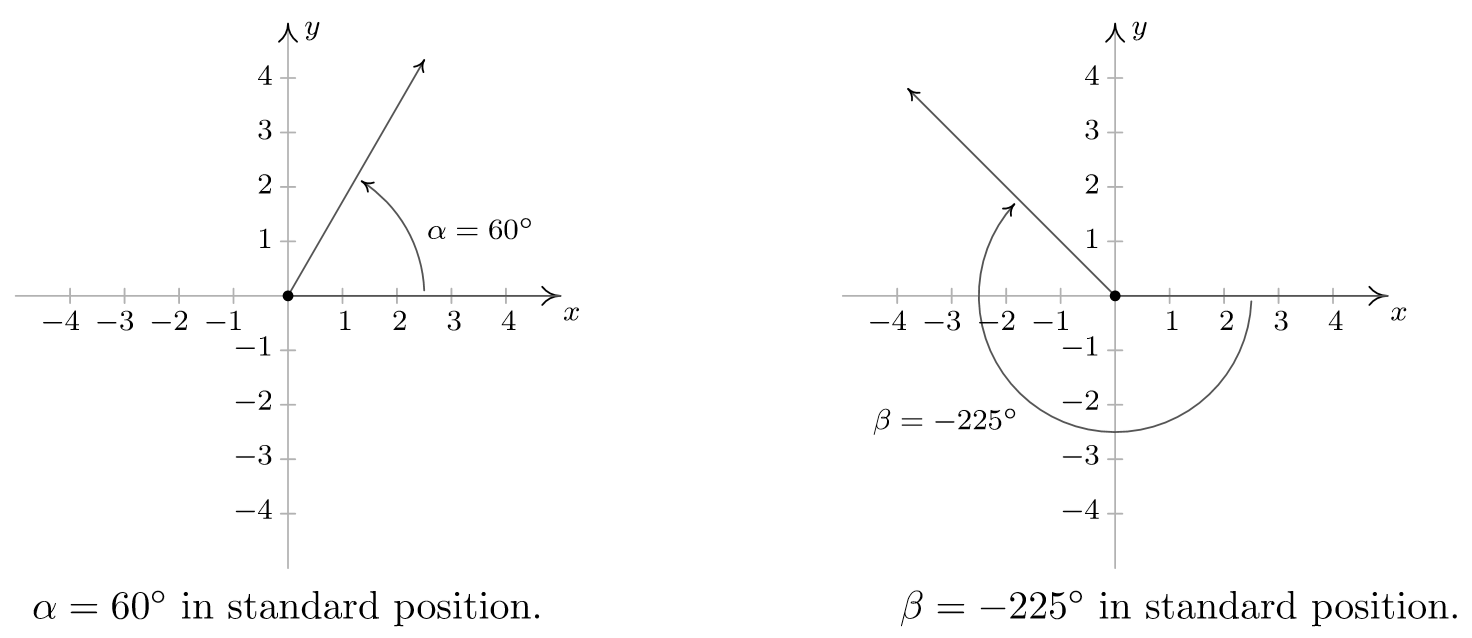
Graph each of the (oriented) angles below in standard position and classify them according to where their terminal side lies. Find three coterminal angles, at least one of which is positive and one of which is negative.
1. \alpha = 60^{\circ} \qquad \qquad 2. \beta = -225^{\circ} \qquad \qquad 3. \gamma = 540^{\circ} \qquad \qquad 4. \phi = -750^{\circ}
Solution
- To graph \alpha = 60^{\circ}, we draw an angle with its initial side on the positive x-axis and rotate counter-clockwise \frac{60^{\circ}}{360^{\circ}} = \frac{1}{6} of a revolution. We see that \alpha is a Quadrant I angle. To find angles which are coterminal, we look for angles \theta of the form \theta = \alpha + 360^{\circ} \cdot k, for some integer k. When k = 1, we get \theta = 60^{\circ} + 360^{\circ} = 420^{\circ}. Substituting k = -1 gives \theta = 60^{\circ} - 360^{\circ} = -300^{\circ}. Finally, if we let k = 2, we get \theta = 60^{\circ} + 720^{\circ} = 780^{\circ}.
- Since \beta = - 225^{\circ} is negative, we start at the positive x-axis and clockwise \frac{225^{\circ}}{360^{\circ}} = \frac{5}{8} of a revolution. We see that \beta is a Quadrant II angle. To find coterminal angles, we proceed as before and compute \theta = -225^{\circ} + 360^{\circ} \cdot k for integer values of k. We find 135^{\circ}, -585^{\circ} and 495^{\circ} are all coterminal with -225^{\circ}.
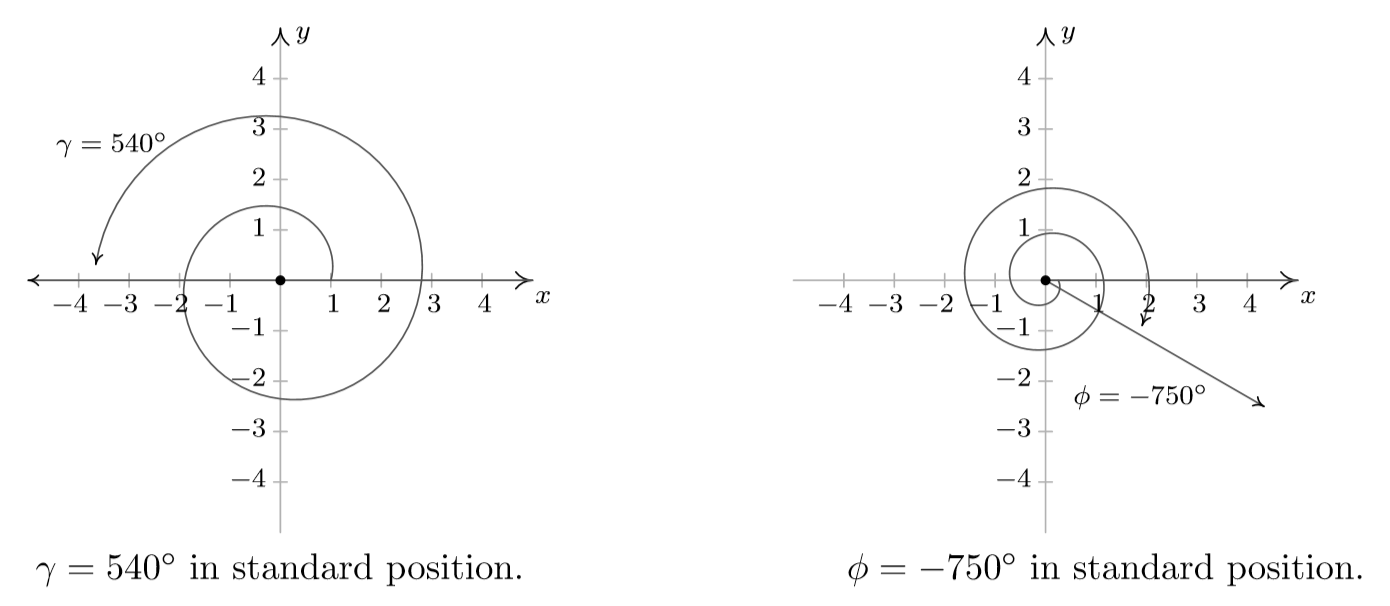
- Since \gamma = 540^{\circ} is positive, we rotate counter-clockwise from the positive x-axis. One full revolution accounts for 360^{\circ}, with 180^{\circ}, or \frac{1}{2} of a revolution remaining. Since the terminal side of \gamma lies on the negative x-axis, \gamma is a quadrantal angle. All angles coterminal with \gamma are of the form \theta = 540^{\circ} + 360^{\circ} \cdot k, where k is an integer. Working through the arithmetic, we find three such angles: 180^{\circ}, -180^{\circ} and 900^{\circ}.
- The Greek letter \phi is pronounced `fee' or `fie' and since \phi is negative, we begin our rotation clockwise from the positive x-axis. Two full revolutions account for 720^{\circ}, with just 30^{\circ} or \frac{1}{12} of a revolution to go. We find that \phi is a Quadrant IV angle. To find coterminal angles, we compute \theta = -750^{\circ} + 360^{\circ} \cdot k for a few integers k and obtain -390^{\circ}, -30^{\circ} and 330^{\circ}.
![]() Try It: \PageIndex{5}
Try It: \PageIndex{5}
- Find an angle α that is coterminal with an angle measuring 870°, where 0°≤α<360°.
- Find an angle β that is coterminal with an angle measuring −300° such that 0°≤β<360°.
Solution
1. α=150° \qquad 2. β=60°
We can find coterminal angles measured in radians in much the same way as we have found them using degrees. In both cases, we find coterminal angles by adding or subtracting one or more full rotations.
Example \PageIndex{6}: Coterminal Angles Using Radians
Find an angle β that is coterminal with \dfrac{19π}{4}, where 0≤β<2π.
Solution
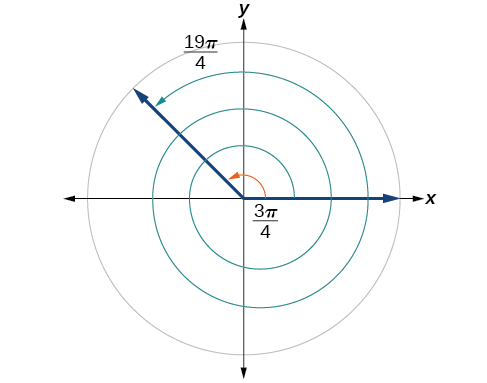
When working in degrees, we found coterminal angles by adding or subtracting 360 degrees, a full rotation. Likewise, in radians, we can find coterminal angles by adding or subtracting full rotations of 2π radians:
\begin{align*} \dfrac{19π}{4}−2π & =\dfrac{19π}{4}−\dfrac{8π}{4} =\dfrac{11π}{4} \nonumber \end{align*}
The angle \dfrac{11π}{4} is coterminal, but not less than 2π, so we subtract another rotation:
\begin{align*} \dfrac{11π}{4}−2π &= \dfrac{11π}{4}−\dfrac{8π}{4} = \dfrac{3π}{4} \nonumber \end{align*}
The angle \dfrac{3π}{4} is coterminal with \dfrac{19π}{4}, as shown in Figure \PageIndex{21}.
Example \PageIndex{7}: Coterminal Angles in Radians
Graph each of the angles below in standard position and classify them according to where their terminal side lies. Find three coterminal angles, at least one of which is positive and one of which is negative.
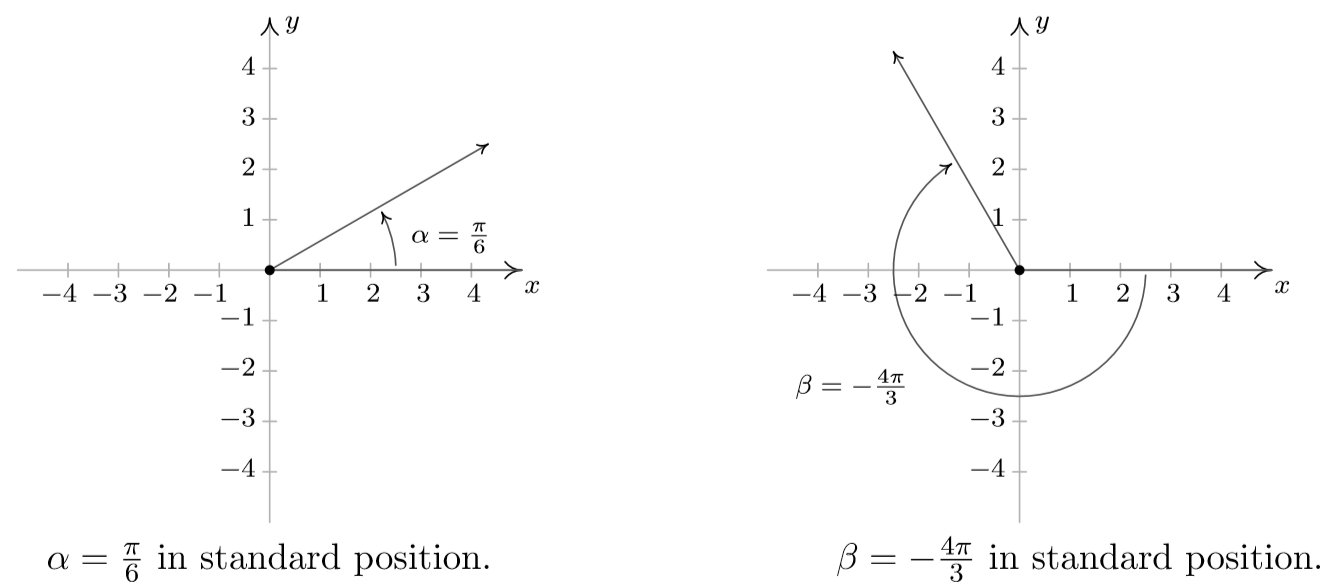
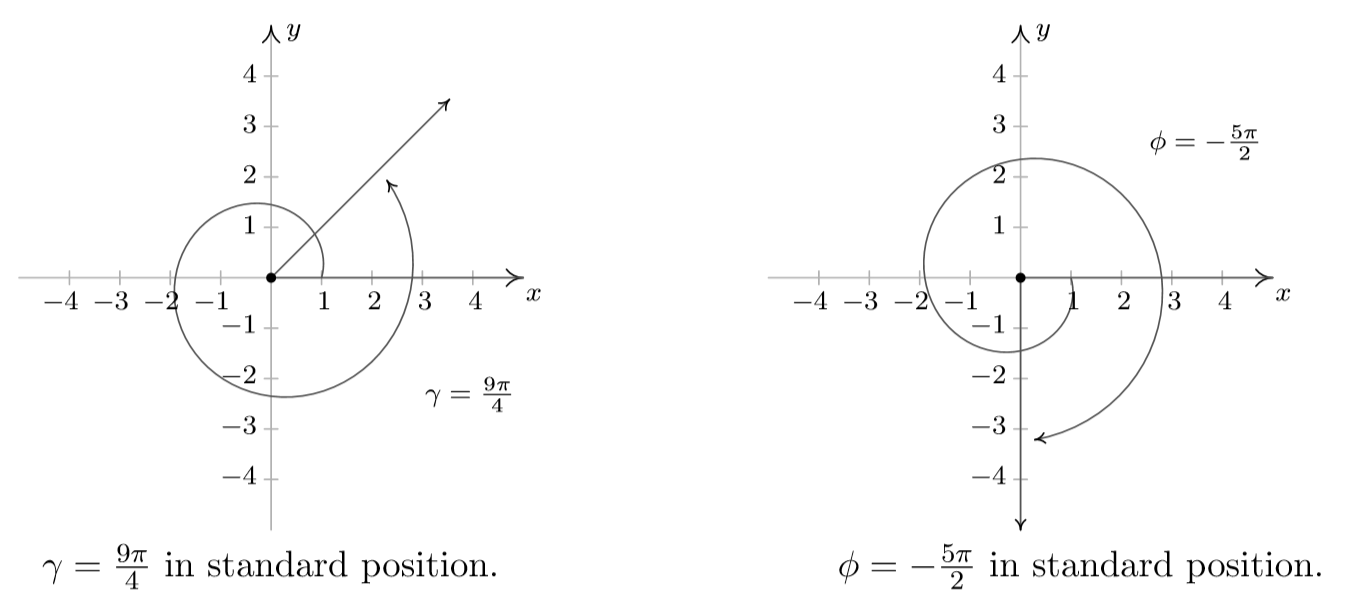
1. \alpha = \dfrac{\pi}{6} \qquad \qquad 2. \beta = -\dfrac{4\pi}{3} \qquad \qquad 3. \gamma = \dfrac{9 \pi}{4} \qquad \qquad 4. \phi = - \dfrac{5 \pi}{2}
Solution
- The angle \alpha = \frac{\pi}{6} is positive, so we draw an angle with its initial side on the positive x-axis and rotate counter-clockwise \frac{\left( \pi / 6\right)}{2 \pi} = \frac{1}{12} of a revolution. Thus \alpha is a Quadrant I angle. Coterminal angles \theta are of the form \theta = \alpha + 2\pi \cdot k, for some integer k. To make the arithmetic a bit easier, we note that 2\pi = \frac{12 \pi}{6}, thus when k = 1, we get \theta = \frac{\pi}{6} + \frac{12 \pi}{6} = \frac{13 \pi}{6}. Substituting k = -1 gives \theta = \frac{\pi}{6} - \frac{12 \pi}{6} = -\frac{11 \pi}{6} and when we let k = 2, we get \theta = \frac{\pi}{6} + \frac{24 \pi}{6} = \frac{25 \pi}{6}.
- Since \beta = - \frac{4\pi}{3} is negative, we start at the positive x-axis and rotate clockwise \frac{\left(4 \pi / 3\right)}{2\pi} = \frac{2}{3} of a revolution. We find \beta to be a Quadrant II angle. To find coterminal angles, we proceed as before using 2\pi = \frac{6 \pi}{3}, and compute \theta = -\frac{4 \pi}{3} + \frac{6 \pi}{3} \cdot k for integer values of k. We obtain \frac{2\pi}{3}, -\frac{10 \pi}{3} and \frac{8 \pi}{3} as coterminal angles.
- \gamma = \frac{9 \pi}{4} is positive, we rotate counter-clockwise from the positive x-axis. One full revolution accounts for 2 \pi = \frac{8 \pi}{4} of the radian measure with \frac{\pi}{4} or \frac{1}{8} of a revolution remaining. We have \gamma as a Quadrant I angle. All angles coterminal with \gamma are of the form \theta = \frac{9 \pi}{4} + \frac{8\pi}{4} \cdot k, where k is an integer. Working through the arithmetic, we find: \frac{\pi}{4}, -\frac{7 \pi}{4} and \frac{17 \pi}{4}.
- To graph \phi = -\frac{5 \pi}{2}, we begin our rotation clockwise from the positive x-axis. As 2 \pi = \frac{4 \pi}{2}, after one full revolution clockwise, we have \frac{\pi}{2} or \frac{1}{4} of a revolution remaining. Since the terminal side of \phi lies on the negative y-axis, \phi is a quadrantal angle. To find coterminal angles, we compute \theta = -\frac{5 \pi}{2} + \frac{4 \pi}{2} \cdot k for a few integers k and obtain -\frac{\pi}{2}, \frac{3 \pi}{2} and \frac{7 \pi}{2}.
![]() Try It: \PageIndex{7}
Try It: \PageIndex{7}
Find an angle of measure θ that is coterminal with an angle of measure −\dfrac{17π}{6} where 0≤θ<2π.
Solution
\dfrac{7π}{6}
Key Concepts
- An angle is formed from the union of two rays, by keeping the initial side fixed and rotating the terminal side. The amount of rotation determines the measure of the angle.
- An angle is in standard position if its vertex is at the origin and its initial side lies along the positive x-axis. A positive angle is measured counterclockwise from the initial side and a negative angle is measured clockwise.
- To draw an angle in standard position, draw the initial side along the positive x-axis and then place the terminal side according to the fraction of a full rotation the angle represents.
- In addition to degrees, the measure of an angle can be described in radians.
- To convert between degrees and radians, use the proportion \frac{θ}{180}=\frac{θ^R}{π}.
- Two angles that have the same terminal side are called coterminal angles.
- We can find coterminal angles by adding or subtracting 360° or 2π.
Glossary
- angle
- the union of two rays having a common endpoint
- coterminal angles
- description of positive and negative angles in standard position sharing the same terminal side
- degree
- a unit of measure describing the size of an angle as one-360th of a full revolution of a circle
- initial side
- the side of an angle from which rotation begins
- measure of an angle
- the amount of rotation from the initial side to the terminal side
- negative angle
- description of an angle measured clockwise from the positive x-axis
- positive angle
- description of an angle measured counterclockwise from the positive x-axis
- quadrantal angle
- an angle whose terminal side lies on an axis
- radian measure
- the ratio of the arc length formed by an angle divided by the radius of the circle
- radian
- the measure of a central angle of a circle that intercepts an arc equal in length to the radius of that circle
- ray
- one point on a line and all points extending in one direction from that point; one side of an angle
- reference angle
- the measure of the acute angle formed by the terminal side of the angle and the horizontal axis
- standard position
- the position of an angle having the vertex at the origin and the initial side along the positive x-axis
- terminal side
- the side of an angle at which rotation ends
- vertex
- the common endpoint of two rays that form an angle
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.

