5.6e: Exercises - Graphs of Other Trigonometric Functions
- Page ID
- 120722
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A: Concepts
Exercise \(\PageIndex{A}\)
1) Explain how the graph of the sine function can be used to graph \(y=\csc x\).
2) How can the graph of \(y=\cos x\) be used to construct the graph of \(y=\sec x\)?
3) Explain why the period of \(y=\tan x\) is equal to \(\pi \).
4) Why are there no intercepts on the graph of \(y=\csc x\)?
5) How does the period of \(y=\csc x\) compare with the period of \(y=\sin x\)?
- Answer
-
1. Since \(y=\csc x\) is the reciprocal function of \(y=\sin x\) , you can plot the reciprocal of the coordinates on the graph of \(y=\sin x\) obtain the \(y\)-coordinates of \(y=\csc x\) . The \(x\)-intercepts of the graph \(y=\sin x\) are the vertical asymptotes for the graph of \(y=\csc x\).
3. Answers will vary. Using the unit circle, one can show that \(y=\tan (x+\pi )=\tan x\).
5. The period is the same: \(2\pi \)add texts here. Do not delete this text first.
B: Graph Equations without Phase Shifts
Exercise \(\PageIndex{B}\)
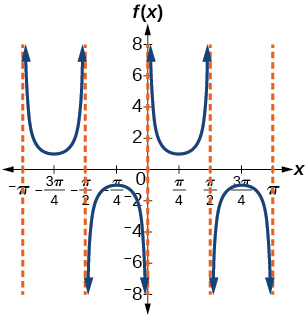
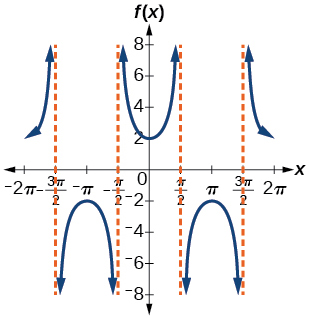
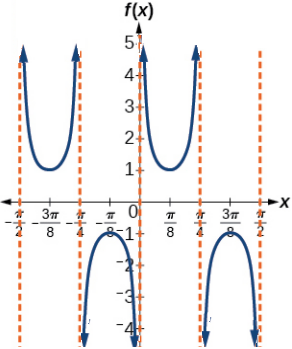
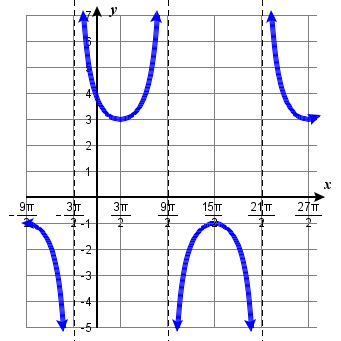
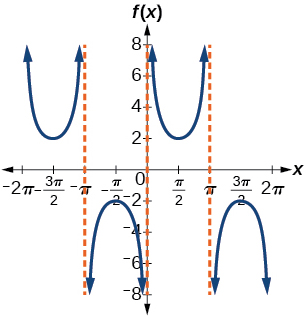
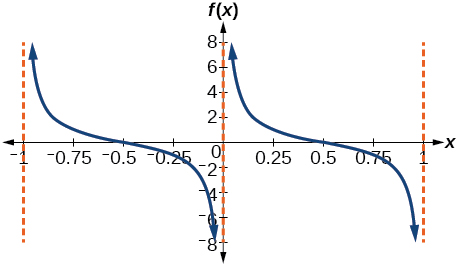
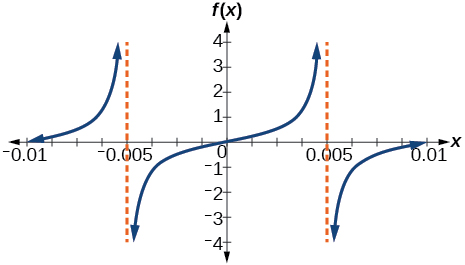
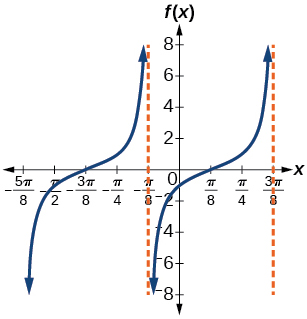
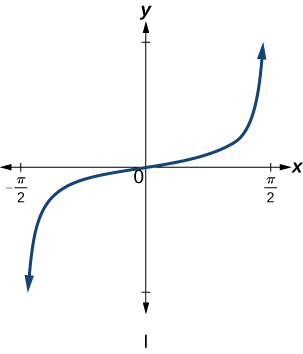
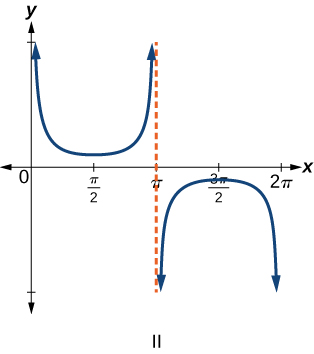
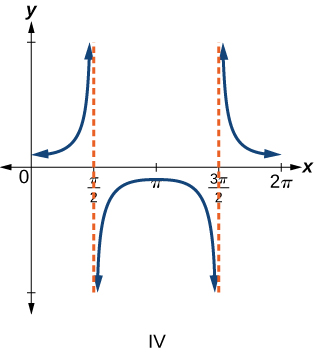
\( \bigstar \) Match each trigonometric function with one of the following graphs.
| 6. \(f(x)=\tan x\) | 7. \(f(x)=\sec x\) | 8. \(f(x)=\csc x\) | 9. \(f(x)=\cot x\) |
 |
 |
 |
 |
\( \bigstar \) For each function, identify attributes of the graph: (a) Stretching factor and vertical shift, (b) period, and (c) asymptotes, (d) domain and range. (e) Sketch two periods of the graph.
|
11. \(f(x)= 4 \tan \left ( \dfrac{1 }{4} x \right ) + 1 \) 12. \(f(x)= 2 \tan (x) - 4 \) 13. \(f(x) = \tan (6x) +3 \) 14. \(f(x)= 2 \tan \left ( \dfrac{\pi }{2} x \right ) +2 \) 15. \(f(x)= - 3 \tan \left ( \dfrac{3 \pi }{2} x \right ) -1 \) 16. \(f(x)= \tan ( \pi x ) \) 17. \(f(x)= \cot \left ( \dfrac{2 }{5} x \right ) - 2 \) 18. \(f(x)= 2 \cot(2x) +2 \) |
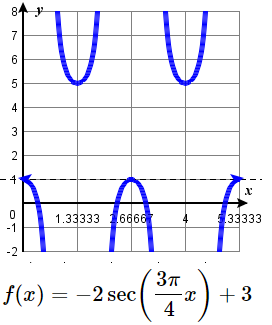
19. \(f(x)= \cot(x) \) 20. \(f(x)= 2 \cot \left ( \dfrac{\pi }{4} x \right ) -1 \) 21. \(f(x)= - \cot \left ( \dfrac{2 \pi }{3} x \right ) + 1 \) 22. \(f(x) = 3\cot(4 \pi x) - 3 \) 23. \(f(x)= \sec \left ( \dfrac{1 }{3} x \right ) -2 \) 24. \(f(x)= 3 \sec (x) + 2 \) 25. \(f(x)= 4 \sec(3x) \) 26. \(f(x)= 2 \sec \left ( \dfrac{2 \pi }{5} x \right ) + 1 \) |
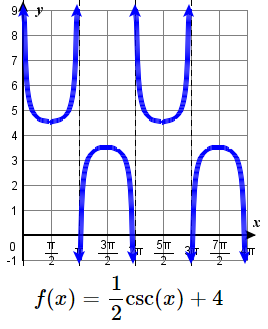
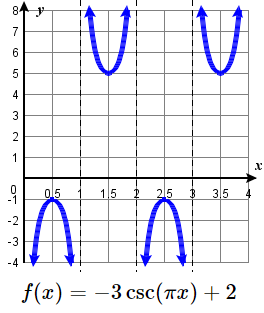
27. \(f(x)= - 2\sec \left ( \dfrac{3 \pi }{4} x \right ) +3 \) 28. \(f(x)= 3 \sec( \pi x) \) 29. \(f(x)= \dfrac{1}{2}\csc(x) + 4\) 30. \(f(x)= 3 \csc \left( \dfrac{2}{3}x \right) -2 \) 31. \(f(x)=2 \csc (x) \) 32. \(f(x)= 2 \csc \left ( \dfrac{ \pi }{3} x \right ) + 1 \) 33. \(f(x)= -3 \csc ( \pi x ) +2 \) 34. \(f(x)= \csc ( 3 \pi x ) -1 \) |
- Answers to Odd Exercises
- \(k\) used below represents any integer
7. \(\mathrm{IV}\) \(\qquad\) 9. \(\mathrm{III}\)11. V stretch factor: 4, up 1.
period: \(4\pi\),
VA: \(x = 2\pi +4 \pi k\)
D: \(\{ x| \ne 2\pi +4 \pi +k \}\)
R: \( (-\infty, \infty) \)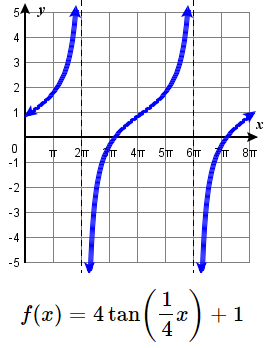
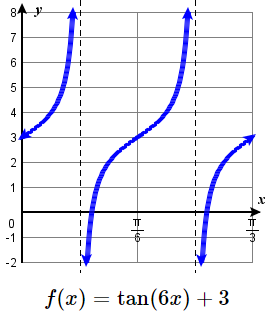
13. no vertical stretch, up 3;
period: \(\pi/6\),
VA: \(x=\tfrac{\pi}{12} + \tfrac{\pi}{6} k\)
D: \(\{ x| \ne \tfrac{\pi}{12} + \tfrac{\pi}{6} k \}\)
R: \( (-\infty, \infty) \)
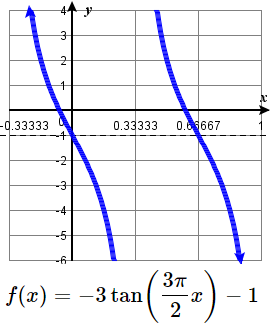
15. \(y \rightarrow -3y\), down 1;
period: \(\tfrac{2}{3}\),
VA: \(x=\tfrac{1}{3} + \tfrac{2}{3}k\)
D: \(\{ x| \ne \tfrac{1}{3} + \tfrac{2}{3}k \}\)
R: \( (-\infty, \infty) \)
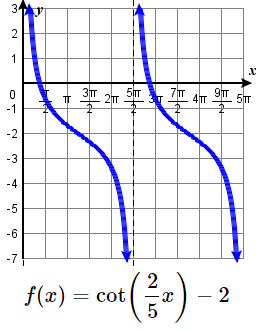
17. no vertical stretch, down 2; period: \(\tfrac{5\pi}{2} \),
VA: \(x=\tfrac{5\pi}{2}k \)
D: \(\{ x| \ne \tfrac{5\pi}{2}k \}\)
R: \( (-\infty, \infty) \)
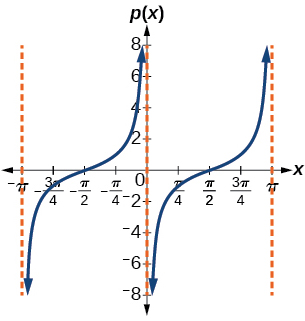
19. no V stretch, no V shift;
period: \(\pi \) ;
VA: \(x=\pi k\)
D: \(\{ x| \ne \pi k \}\)
R: \( (-\infty, \infty) \)
21. reflection over \(x\)-axis, up 1;
period: \(1.5\);
VA: \(x = 1.5k\)
D: \(\{ x| \ne 1.5k \}\)
R: \( (-\infty, \infty) \)
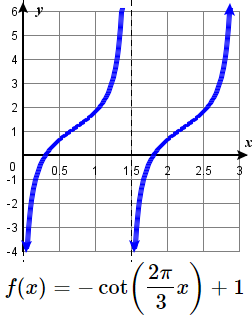
23. no vertical stretch, down 2;
period: \( 6\pi \),
VA: \(x=1.5\pi +3\pi k\)
D: \(\{ x| \ne 1.5\pi +3\pi k \}\)
R: \( (-\infty, -3] \cup [-1, \infty) \)
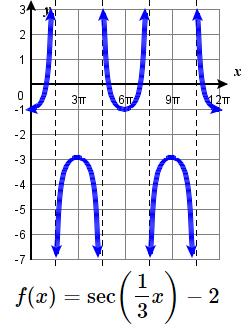
25. V stretching factor: \(4\);
period: \(\frac{2\pi }{3}\) ;
VA: \(x=\frac{\pi }{6} + \tfrac{\pi}{3} k \)
D: \(\{ x| \ne \frac{\pi }{6} + \tfrac{\pi}{3}k \}\)
R: \( (-\infty, -4] \cup [4, \infty) \)
27. \(y \rightarrow -2y\), up 3;
period: \( \tfrac{8}{3} \),
VA: \(x= \tfrac{2}{3} +\tfrac{4}{3} k\)
D: \(\{ x| \ne \tfrac{2}{3} +\tfrac{4}{3} k \}\)
R: \( (-\infty, 1] \cup [5, \infty) \)
29. \(y \rightarrow \tfrac{1}{2} y\), up 4;
VA: \( 2\pi \),
VA: \(x= \pi k\)
D: \(\{ x| \ne \pi k \}\)
R: \( (-\infty, 3.5] \cup [4.5, \infty) \)
31. V stretch factor: \(2\);
period: \(2\pi \) ;
VA: \(x=\pi k\)
D: \(\{ x| \ne \pi k \}\)
R: \( (-\infty, -2] \cup [2, \infty) \)
33. \(y \rightarrow -3y\), up 2;
period: \( 2 \),
VA: \(x= k\)
D: \(\{ x| \ne k \}\)
R: \( (-\infty, -1] \cup [5, \infty) \)
C: Graph Equations with Phase Shifts
Exercise \(\PageIndex{C}\)
\( \bigstar \) For each function, identify attributes of the graph: (a) Stretching factor and vertical shift, (b) period, (c) phase shift, and (d) asymptotes, (e) domain and range. (f) Sketch two periods of the graph.
|
41. \(f(x)=\tan \left ( x+\dfrac{\pi }{4} \right )\) 42. \(f(x)=4 \tan(\pi x- \pi)-5\) 43. \(f(x)=2\tan(4x-32)\) 44. \(g\left(x\right)=3\tan \left(6x+42\right)\) 45. \(y=\cot\left(3x-\dfrac{\pi}{4} \right)+2\) |
46. \(f(x)=5 \cot \left(x+\dfrac{\pi }{2} \right) -3 \) 49. \(h(x)=2\sec\left(\dfrac{\pi }{4}(x+1) \right)\) 50. \(f(x)=3\sec \left( \dfrac{\pi }{2}x-\dfrac{\pi }{3} \right)-2\) 51. \(f(x)=2\sec \left(x - \dfrac{\pi }{4} \right)-1\) |
52. \(k\left(x\right)=3\sec \left(2\left(x+\dfrac{\pi }{2} \right)\right)~\) 53. \(m(x)=6\csc\left(\dfrac{\pi }{3}x+\pi \right)\) 54. \(n\left(x\right)=4\csc \left(\dfrac{5\pi }{3} x-\dfrac{20\pi }{3} \right) +1\) 55. \(f(x)=\dfrac{7}{5}\csc \left(x-\dfrac{\pi }{4} \right)\) 56. \(n\left(x\right)=4\csc \left(\dfrac{\pi }{4} x + \dfrac{\pi }{20} \right) + 3\) |
57. Construct an equation and graph a tangent curve, \(A=1\)period of \(\dfrac{\pi }{3}\)and phase shift \((h, k)=\left ( \dfrac{\pi }{4},2 \right )\)
58. Construct an equation and graph a tangent curve, \(A=-2\), period of \(\dfrac{\pi }{4}\); and phase shift \((h, k)=\left (- \dfrac{\pi }{4},-2 \right )\)
- Answers to odd exercises:
- \(k\) used below represents any integer
41. No V stretch, no V shift;
period: \(\pi \); shift left \(\tfrac{ \pi}{4}\) units;
VA: \(x=\frac{\pi}{4}+\pi k\)
D: \(\{ x| \ne \frac{\pi}{4}+\pi k \}\)
R: \( (-\infty, \infty) \)
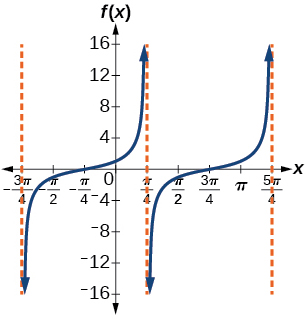
43. \( y \rightarrow 2y \), no V shift;
period: \(\frac{\pi }{4}\); shift right \(8\) units (the point (8, 0) is on the graph);
VA: \(x=\frac{1}{4}\left(\frac{\pi }{2}+\pi k \right)+8\)
D: \(\{ x| \ne \frac{1}{4}\left(\frac{\pi }{2}+\pi k \right)+8 \}\)
R: \( (-\infty, \infty) \)
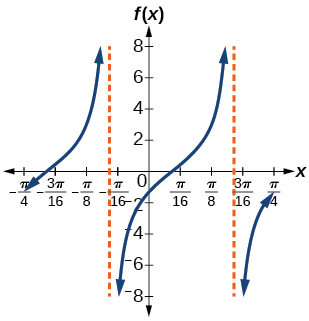
45. No vertical stretch, up \(2\);
period: \( \pi /3 \); shift right \(\tfrac{ \pi}{12}\);
VA: \( x= \tfrac{ \pi}{12}+ \tfrac{ \pi}{3} k \)
D: \(\{ x| \ne \tfrac{ \pi}{12}+ \tfrac{ \pi}{3} k \}\)
R: \( (-\infty, \infty) \)
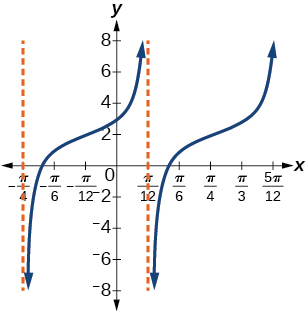
49. \( y \rightarrow 2y \), no vertical shift;
period: \(8\); shift left \(1\) unit;
VA: \(x = 1 + 4k\)
D: \(\{ x| \ne 1 + 4k \}\)
R: \( (-\infty, -2] \cup [2, \infty) \)
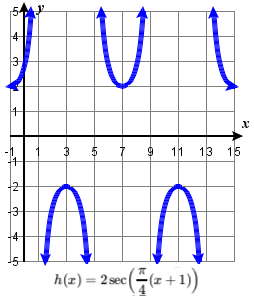
51. V stretch factor: \(2\); down 1
period: \(2\pi \); shift right \( \tfrac{\pi}{4} \) units;
VA: \(x=-\tfrac{\pi}{4}+\pi k\)
D: \(\{ x| \ne -\tfrac{\pi}{4}+\pi k \}\)
R: \( (-\infty, -3] \cup [1, \infty) \)
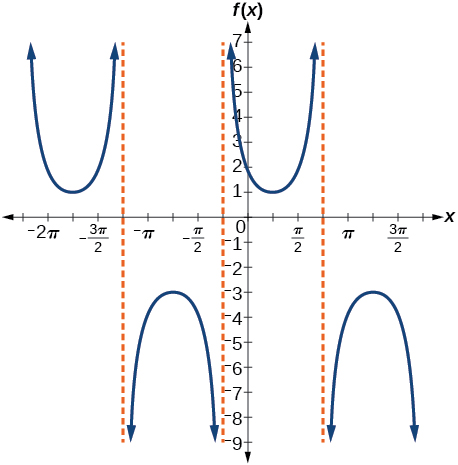
53. V stretch factor: \(6\);
period: \(6\); shift left \(3\) units;
VA: \(x=3k\)
D: \(\{ x| \ne 3k \}\)
R: \( (-\infty, -6] \cup [6, \infty) \)
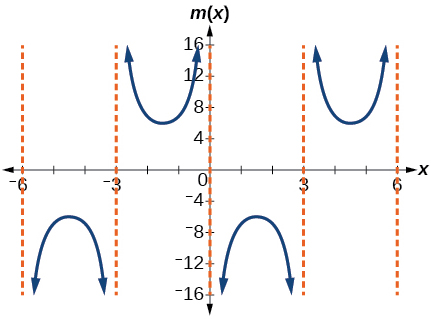
55. V stretch factor: \(\frac{7}{5}\);
VA: \(2\pi \); shift right \( \tfrac{\pi}{4} \) units;
VA: \(x=\tfrac{\pi}{4}+\pi k\)
D: \(\{ x| \ne \tfrac{\pi}{4}+\pi k \}\)
R: \( (-\infty, -\frac{7}{5}] \cup [\frac{7}{5}, \infty) \)
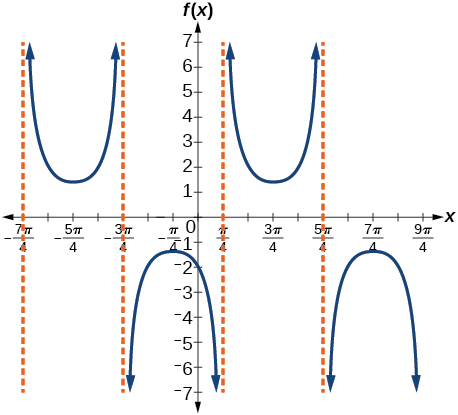
D: Practice Negative Angle Identities
Exercise \(\PageIndex{D}\)
|
61. If \(\tan x=-1.5\) , find \(\tan (-x)\). 62. If \(\sec x=2\), find \(\sec (-x)\). 63. If \(\csc x=-5\), find \(\csc (-x)\). 64. If \(x\sin x=2\), find \((-x)\sin (-x)\). |
65. If \(\tan x=3\), find \(\tan \left(-x\right)\). 66. If \(\sec x=-4\), find \(\sec \left(-x\right)\). 67. If \(\csc x=2\), find \(\csc \left(-x\right)\). |
Rewrite each expression such that the argument \(x\) is positive. 69. \(\cot(-x)\cos(-x)+\sin(-x)\) 70. \(\cos(-x)+\tan(-x)\sin(-x)\) |
- Answers to odd exercises:
-
61. \(1.5\) \(\qquad\) 63. \(5\) \(\qquad\) 65. \(-3\) \(\qquad\) 67. \(-2\) \(\qquad\) 69. \(-\cot x \cos x-\sin x\)
E: Given a graph, construct an equation
Exercise \(\PageIndex{E}\)
\( \bigstar \) Find an equation for the graph of each function.
|
71.
|
72.
|
73.
|
74. |
|
75.
|
76.
|
77.
|
78.
|
79.  |
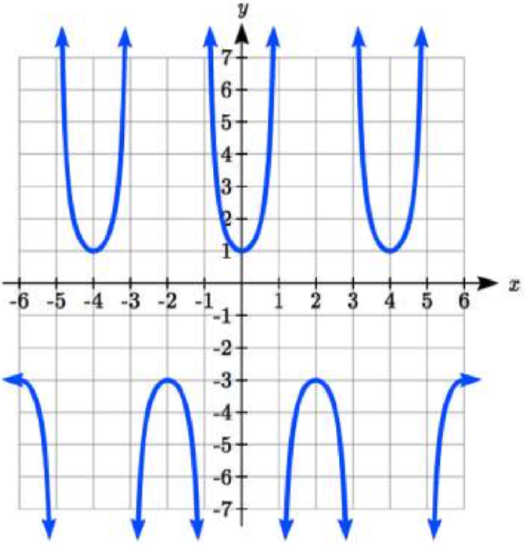80. |
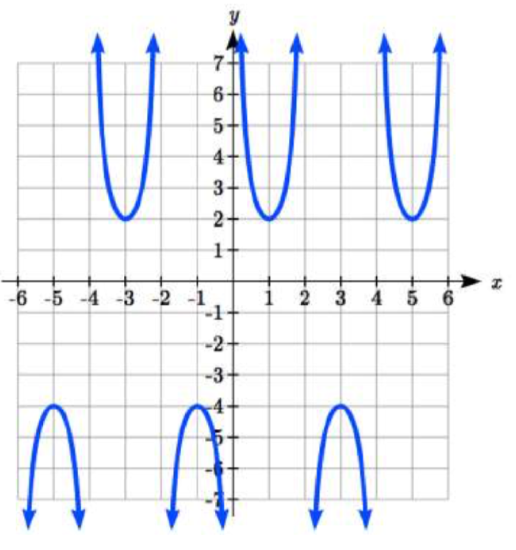81.  |
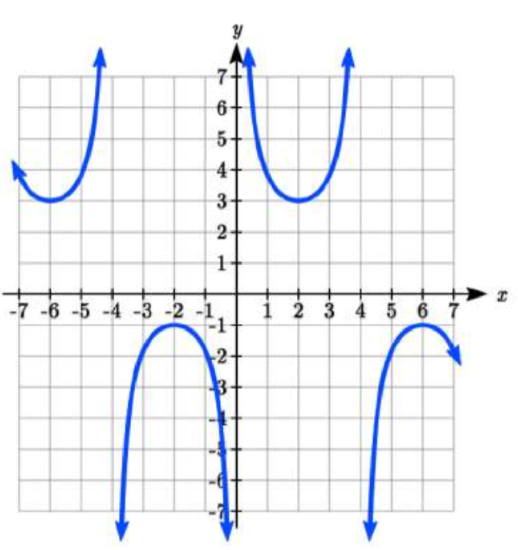82.  |
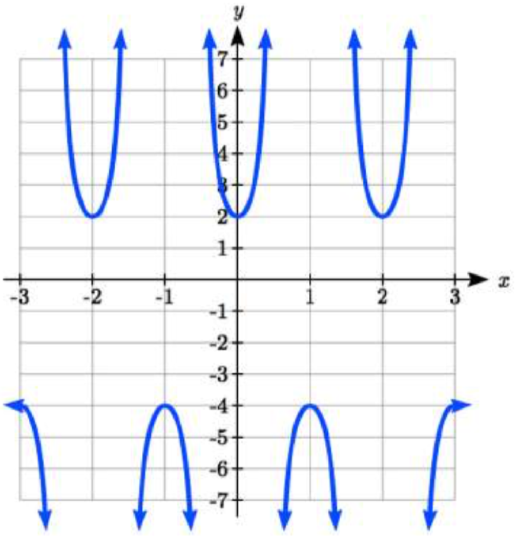- Answers to odd exercises:
-
71. \(f(x)=\csc (2x)\) \(\qquad\) 73. \(f(x)=\csc (4x)\) \(\qquad\) 75. \(f(x)=2\csc x\) \(\qquad\) 77. \(f(x)=\dfrac{1}{2}\tan (100\pi x)\)
79. \(f(x) = 2 \sec(\dfrac{\pi}{2} x) - 1\) \(\qquad\) 81. \(f(x) = 2 \csc(\dfrac{\pi}{4} x ) + 1\)
F: Applications
Exercise \(\PageIndex{F}\)
90. The function \(f(x)=20\tan\left(\dfrac{\pi }{10}x\right)\) marks the distance in the movement of a light beam from a police car across a wall for time \(x\)in seconds, and distance \(f(x)\) in feet.
- Graph on the interval \([0,5]\)
- Find and interpret the stretching factor, period, and asymptote.
- Evaluate \(f(10)\) and \(f(2.5)\) and discuss the function’s values at those inputs.
91. St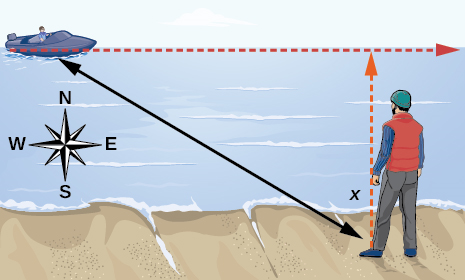
anding on the shore of a lake, a fisherman sights a boat far in the distance to his left. Let \(x\) measured in radians, be the angle formed by the line of sight to the ship and a line due north from his position. Assume due north is \(0\) and \(x\) is measured negative to the left and positive to the right. (See Figure below.) The boat travels from due west to due east and, ignoring the curvature of the Earth, the distance \(d(x)\) in kilometers, from the fisherman to the boat is given by the function \(d(x)=1.5\sec(x)\)
- What is a reasonable domain for \(d(x)\)?
- Graph \(d(x)\) on this domain.
- Find and discuss the meaning of any vertical asymptotes on the graph of \(d(x)\).
- Calculate and interpret \(d\left ( -\dfrac{\pi }{3} \right )\) Round to the second decimal place.
- Calculate and interpret \(d\left ( \dfrac{\pi }{6} \right )\) Round to the second decimal place.
- What is the minimum distance between the fisherman and the boat? When does this occur?
- 91. Answer
-
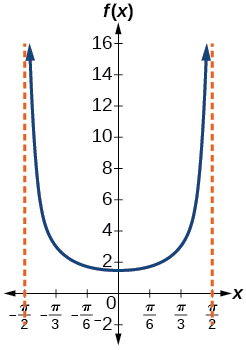\(\left ( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right )\)- see diagram on the right -->
- \(x=-\dfrac{\pi }{2}\) and \(x=\dfrac{\pi }{2}\)the distance grows without bound as \(| x |\) approaches \(\dfrac{\pi }{2}\)—i.e., at right angles to the line representing due north, the boat would be so far away, the fisherman could not see it;
- \(3\); when \(x=-\dfrac{\pi }{3}\)the boat is \(3\) km away;
- \(1.73\); when \(x=\dfrac{\pi }{6}\)the boat is about \(1.73\) km away;
- \(1.5\) km; when \(x=0\)
92. A laser rangefinder is locked on a comet approaching Earth. The distance \(g(x)\)in kilometers, of the comet after \(x\) days, for \(x\) in the interval \(0\) to \(30\) days, is given by \(g(x)=250,000\csc \left(\dfrac{\pi }{30}x \right)\).
- Graph \(g(x)\) on the interval \([0,35]\).
- Evaluate \(g(5)\) and interpret the information.
- What is the minimum distance between the comet and Earth? When does this occur? To which constant in the equation does this correspond?
- Find and discuss the meaning of any vertical asymptotes.
93. A video camera is focused on a rocket on a launching pad \(2\) miles from the camera. The angle of elevation from the ground to the rocket after \(x\) seconds is \(\dfrac{\pi }{120}x\).
- Write a function expressing the altitude \(h(x)\)in miles, of the rocket above the ground after \(x\) seconds. Ignore the curvature of the Earth.
- Graph \(h(x)\) on the interval \((0,60)\).
- Evaluate and interpret the values \(h(0)\) and \(h(30)\).
- What happens to the values of \(h(x)\) as \(x\) approaches \(60\) seconds? Interpret the meaning of this in terms of the problem.
93. Answer-
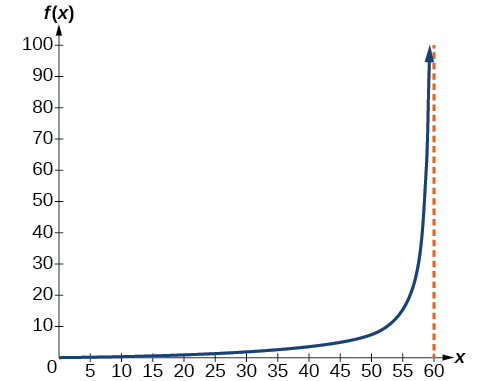
- \(h(x)=2\tan \left(\dfrac{\pi }{120}x \right)\)
- \(h(0)=0\)after \(0\) seconds, the rocket is \(0\) mi above the ground; \(h(30)=2\)after \(30\) seconds, the rockets is \(2\) mi high;
- As \(x\) approaches \(60\) seconds, the values of \(h(x)\) grow increasingly large. The distance to the rocket is growing so large that the camera can no longer track it.