5.6: Graphs of the Other Trigonometric Functions

Learning Objectives

• Graph \(y=\tan x\),  \(y=\cot x\), \(y=\sec x\), and \(y=\csc x\), and transformations of these functions.
• Construct an equation from a graph of a transformation of  \(y=\tan x\).

We know the tangent function can be used to find distances, such as the height of a building, mountain, or flagpole. But what if we want to measure repeated occurrences of distance? Imagine, for example, a police car parked next to a warehouse. The rotating light from the police car would travel across the wall of the warehouse in regular intervals. If the input is time, the output would be the distance the beam of light travels. The beam of light would repeat the distance at regular intervals. The tangent function can be used to approximate this distance. Asymptotes would be needed to illustrate the repeated cycles when the beam runs parallel to the wall because, seemingly, the beam of light could appear to extend forever. The graph of the tangent function would clearly illustrate the repeated intervals. In this section, we will explore the graphs of the tangent and other trigonometric functions.

Analyzing the Graph of \(y =\tan x\)

We can determine whether tangent is an odd or even function by using the definition of tangent and the Negative Angle Properties for sine and cosine.

\( \tan(-x)= \dfrac{\sin(-x)}{\cos(-x)} = \dfrac{-\sin \, x}{\cos \, x} = -\dfrac{\sin \, x}{\cos \, x} = -\tan \, x \)

Therefore, tangent is an odd function. We can further analyze the graphical behavior of the tangent function by looking at values for some of the special angles, as listed in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\)

\(x\)	\(−\dfrac{\pi}{2}\)	\(−\dfrac{\pi}{4}\)	0	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{3\pi}{4}\)	\(\pi\)	\(\dfrac{5\pi}{4}\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{7\pi}{4}\)	\(2\pi\)
\(\tan x\)	undefined	\(–1\)	\(0\)	\(1\)	undefined	\(-1\)	\(0\)	\(1\)	undefined	\(-1\)	\(0\)

These points will help us draw our graph, but we need to determine how the graph behaves where it is undefined. If we look more closely at values when when \(-\dfrac{\pi}{2}<x<-\dfrac{\pi}{4}\), and when \(\dfrac{\pi}{4}<x<\dfrac{\pi}{2}\), we can use a table to look for a trend. Because \(\dfrac{\pi}{4}≈0.79\) and \(\dfrac{\pi}{2}≈1.57\), we choose values of \(x\) in Table \(\PageIndex{2}\) below, for which \(-1.57<x<-0.79\)  and \(0.79<x<1.57\). 

Table \(\PageIndex{2}\)

−1.56	−1.55	−1.5	−1.3	-1	\(x\)	1	1.3	1.5	1.55	1.56
−92.6	−48.1	−14.1	−3.6	-1.6	\(\tan x\)	1.6	3.6	14.1	48.1	92.6

Figure \(\PageIndex{1}\): Graph of the tangent function

We can see that, as \(x\) approaches \(\dfrac{\pi}{2}\) or \(−\dfrac{\pi}{2}\), the magnitude of the outputs of the function grow without bound, so the graph of the tangent function has vertical asymptotes at these values. This behaviour is a result of the fact that \(\tan(x) = \dfrac{\sin(x)}{\cos(x)}\), and the cosine function can be zero. At every value of \(x\) for which \(\cos(x)=0\), the tangent function is undefined, and the graph of the tangent function is discontinuous.

The period of the tangent function is \(\pi\) because the graph repeats itself on intervals of \(k\pi\) where \(k\) is an integer. Examining the graph of the tangent function on \(−\frac{\pi}{2}\) to \(\frac{\pi}{2}\), we can see the behavior of the graph completes one cycle. If we look at any larger interval, we will see that the characteristics of the graph repeat.

Graph a Stretched or Compressed Tangent Function

As with the sine and cosine functions, the tangent function can be described by a general equation: \(\boxed{y=A\tan(Bx)}\)

We can identify horizontal and vertical stretches and compressions using values of \(A\) and \(B\). The horizontal stretch can typically be determined from the period of the graph. With tangent graphs, it is often necessary to determine a vertical stretch using a point on the graph.

Because there are no maximum or minimum values of a tangent function, the term amplitude cannot be interpreted as it is for the sine and cosine functions. Instead, we will use the phrase stretching/compressing factor when referring to the constant \(A\).

FEATURES OF THE GRAPH OF \(y = A \tan(Bx)\)

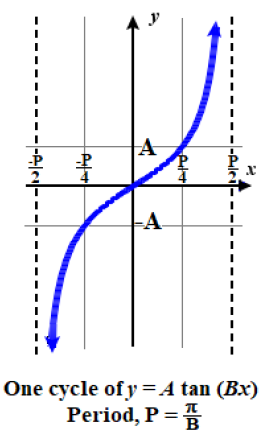
• The vertical stretching factor is \(|A|\). 
• The period is \(P=\dfrac{\pi}{|B|}\).
• The asymptotes occur at \(x=\dfrac{P}{2}+P \cdot k\) where \(k\) is any integer and \(P\) is the period.
• The domain is all real numbers \(x\), where \( \{ x | x≠\dfrac{P}{2}+P \cdot k \}\) where \(k\) is any integer and \(P\) is the period.
• The range is \((−\infty,\infty)\).
• \(y=A\tan(Bx)\) is an odd function.

Figure \(\PageIndex{2a}\): Generic Graph for \(y = A \tan (Bx)\), with \(A\) and \(B\) both positive (or both negative). 

These results can be confirmed by examining the start of a cycle of \(f(x) = A \tan(Bx)\) and relating it to the behaviour of the parent function \(y = \tan (x)\). A cycle for \(f\) starts when its argument \(Bx = -\dfrac{\pi}{2}\) and ends when \(Bx = \dfrac{\pi}{2}\). Solving these equations we obtain the cycle for \(f\) starts when \(x=\dfrac{-\pi}{2B}\), ends when \(x=\dfrac{\pi}{2B}\), and consequently has a length (known as the period) of \(\dfrac{\pi}{B}\). The vertical stretch factor is \(A\) by what we know about transformations. When the argument of \(f\), \(Bx\), is \(\dfrac{\pi}{4}\), the value of \(f\) is \(A \tan \dfrac{\pi}{4} = A\), whereas the value of the parent function with that same argument \(\dfrac{\pi}{4}\), has a value of just \(1\).

We can use what we know about the properties of the tangent function to quickly sketch a graph of any stretched and/or compressed tangent function of the form \(f(x)=A\tan(Bx)\). We focus on a single period of the function including the origin, because the periodic property enables us to extend the graph to the rest of the function’s domain if we wish. Our limited domain is then the interval \(\left (−\dfrac{P}{2},\dfrac{P}{2} \right )\) and the graph has vertical asymptotes at \(\pm \dfrac{P}{2}\) where \(P=\dfrac{\pi}{B}\). On the interval \(\left (−\dfrac{P}{2},\dfrac{P}{2} \right )\), the graph will come up from the left asymptote at \(x=−\dfrac{P}{2}\), cross through the origin, and continue to increase as it approaches the right asymptote at \(x=\dfrac{P}{2}\). To make the function approach the asymptotes at the correct rate, we also need to set the vertical scale by actually evaluating the function for three other quarter points that the graph will pass through. For example, we can use

\(   f \left (\dfrac{P}{4} \right )=A\tan \left (B \cdot \dfrac{P}{4} \right )=A\tan \left (B \cdot \dfrac{\pi}{4B} \right )=A\tan \left (\dfrac{\pi}{4} \right )= A\cdot 1 = 1     \)

 Howto: Given the function \(f(x)=A \tan(Bx)\), graph one period.

Rewrite the equation so that \(B\) is positive. Express the equation in the form \(f(x)=A \tan(Bx)\).

1. Identify the verticalstretching factor, \(| A |\). If \(A\) is negative, the graph will be a reflection over the \(x\)-axis and will be decreasing (rather than increasing) within a cycle.
2. Identify B and determine the period, \(P=\dfrac{\pi}{| B |}\). 
3. Evaluate the \(x\) values for the five quarter points, starting at \(-\dfrac{P}{2}\) and spaced \(\dfrac{P}{4}\) units apart.
4. Draw vertical asymptotes at the first and last quarter points, \(x=−\dfrac{P}{2}\) and \(x=\dfrac{P}{2}\).
5. Evaluate the function at the middle three quarter points and draw the graph through these points. 

In summary, quarter point values of \(x\) and corresponding values for \(f(x)=A \tan(|B|x)\) for one cycle are shown in the table below.

\( \begin{array}{|c|c||c|c| c |}
\hline
x = -\dfrac{P}{2} & x = -\dfrac{P}{4} & x = 0 & x = \dfrac{P}{4} & x = \dfrac{P}{2} \\[4pt]
\hline
\text{asymptote} & y = -A & y = 0 & y = A & \text{asymptote}\\
\hline \end{array} \)

Example \(\PageIndex{1}\): Sketching a Compressed Tangent

Sketch a graph of one period of the function \(y=0.5\tan \left (\dfrac{\pi}{2}x \right )\). State the domain and range.

Solution

First, we identify \(A\) and \(B\).

Figure \(\PageIndex{2b}\)

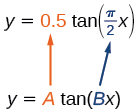
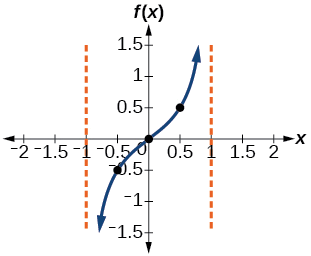
The period is \(P=\dfrac{\pi}{B}=\cfrac{\pi}{\dfrac{\pi}{2}}=2\). The asymptotes are at  \(x=\pm\dfrac{P}{2}=\pm\dfrac{2}{2}\). Therefore, the asymptotes are at  \(x=-1\) and \(x=1\).

The horizontal distance between quarter points is \(\dfrac{P}{4}=0.5\), so quarter points from the start of this cycle (at \(x=-1\), the asymptote on the left, occur at \(x= -1, \; -.5, \; 0, \; .5,\) and \(1\)

\[\begin{align*}
f\left(-\dfrac{P}{4}\right)&= f(-0.5) &&=0.5\tan \left (\dfrac{-0.5\pi}{2} \right )&&= 0.5\tan \left (\dfrac{-\pi}{4} \right )&&= -0.5 = -A\\[4pt]
f(0)&= f(0) &&=0.5\tan \left (\dfrac{0 \cdot \pi}{2} \right )   &&= 0.5 \cdot 0 &&= 0\\[4pt]
f\left(\dfrac{P}{4}\right)&= f(0.5) &&=0.5\tan \left (\dfrac{0.5\pi}{2} \right )  &&= 0.5\tan \left (\dfrac{\pi}{4} \right )&&= 0.5 = A\\[4pt]
\end{align*}\]

This means the curve must pass through the points \((−0.5,−0.5)\), \((0,0)\), and \((0.5,0.5)\).

Domain is \( \{ x | x \ne 1+2k \}\), \(k\) is any integer. Range: \((−\infty,\infty)\).

Figure \(\PageIndex{2c}\) One period of the function \(y=0.5\tan \left (\dfrac{\pi}{2}x \right )\).

 Try It \(\PageIndex{2}\)

Sketch a graph of \(f(x)=3\tan \left (\dfrac{\pi}{6}x \right )\). State the domain and range.

Answer

Vertical stretch is 3; Period (Horizontal stretch) is \(P=\dfrac{\pi}{\dfrac{\pi}{6}}=6\); quarter point \(x\) values, starting at \(-3\) and \(1.5\) units apart, are \(x= -3,\; -1.5,\; 0,\; 1.5,\; 3\); Asymptotes at \(x = -3\) and \(x = 3\); middle quarter point coordinates: \((−1.5,−3)\), \((0,0)\), and \((1.5,\; 3)\). Domain: \( \{ x | x \ne 3+6k \}\), \(k\) is any integer. Range: \((−\infty,\infty)\).

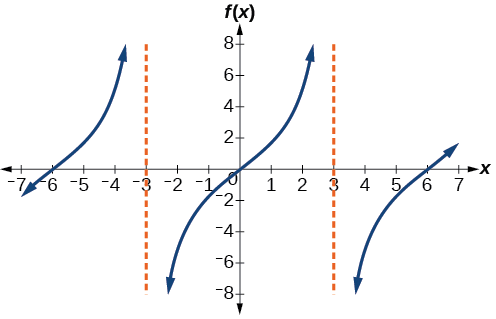
Figure \(\PageIndex{2d}\)  Graph of \(f(x)=3\tan \left (\dfrac{\pi}{6}x \right )\).

Graph a Vertically or Horizontally Shifted Tangent Function

Now that we can graph a tangent function that is stretched or compressed, we will add a vertical shift and/or a phase shift (horizontal shift). In this case, we add \(C\) and \(D\) to the general form of the tangent function, \(f(x)=A\tan(Bx−C)+D \).

FEATURES OF THE GRAPH OF \(g(x) = A\tan(Bx−C)+D\)

• The vertical stretching factor is \(| A |\). There is no amplitude. 
• The period is \(P = \dfrac{\pi}{| B |}\).
• The phase shift is \(H = \dfrac{C}{B}\) units (right when \(H\) is positive, left when \(H\) is negative).
• The vertical shift is \(D\) units (up when \(D\) is positive, down when \(D\) is negative) 
• The vertical asymptotes occur at \(x = H + \dfrac{P}{2}+P \cdot k\), where \(k\) is any integer.
• The domain is \( \{x | x≠ H + \dfrac{P}{2}+P \cdot k \} \), where \(k\) is any integer.
• The range is \((−∞,∞)\).

The graph of this transformed tangent function is fundamentally the generic tangent function \(y = A \tan (Bx)\), that has been shifted \(H\) units right or left and \(D\) units up or down'.

 Howto: Given the function \(y=A\tan(Bx−C)+D\), sketch the graph of one period.

Rewrite the equation so that \(B\) is positive. Express the function in the form \(y=A\tan(Bx−C)+D\).

1. Identify the vertical stretching factor, \(| A |\). (If \(A\) is negative, the graph will be a reflection over the \(x\)-axis and will be decreasing (rather than increasing) within a cycle.) 
2. Identify \(B\) and determine the period, \(P = \dfrac{\pi}{|B|}\).
3. Identify \(C\) and determine the phase shift, \(H = \dfrac{C}{B}\).
4. Evaluate the \(x\) values for the five quarter points, starting at \(x=-\dfrac{P}{2}\) and spaced \(\dfrac{P}{4}\) units apart.
5. Draw vertical asymptotes at the first and last quarter points, \(x=−\dfrac{P}{2}+H\) and \(x=\dfrac{P}{2}+H\).
6. Identify \(D\), which is the vertical shift. 
7. Evaluate the function at the middle three quarter points and draw the graph through these points. Notice that each of these points are the middle three points from the graph of \(y = A \tan (Bx)\), that have had \(H\) added to their \(x\) coordinates, and \(D\) added to their \(y\) coordinates.

In summary, quarter point values of \(x\) and corresponding values for \(g(x)=A \tan(|B|x-C)+D\) for one cycle are shown in the table below.

\( \begin{array}{|c|c||c|c| c |}
\hline
x = -\dfrac{P}{2} +H & x = -\dfrac{P}{4}+H & x = H & x = \dfrac{P}{4}+H & x = \dfrac{P}{2}+H \\[4pt]
\hline
\text{asymptote} & y = -A+D & y = D & y = A+D & \text{asymptote}\\
\hline \end{array} \)

Example \(\PageIndex{3}\): Graphing One Period of a Shifted Tangent Function

Graph one period of the function \(y=−2\tan(\pi x+\pi)−1\). State the domain and range.

Solution

• The function is already written in the form \(y=A\tan(Bx−C)+D\), with \(B > 0\).
• Step 1. \(A=−2\), so the vertical stretching factor is \(|A|=2\). Because \(A\) is negative the graph is decreasing over one cycle.
• Step 2. \(B=\pi\), so the period is \(P=\dfrac{\pi}{| B |}=\dfrac{\pi}{\pi}\). So \(P = 1\).
• Step 3. \(C=−\pi\), so the phase shift is \(H=\dfrac{C}{B}=\dfrac{−\pi}{\pi}\). So \(H = -1\), corresponding to a 1 unit shift to the left. 
• Step 4. The five quarter points start at \(x=H−\dfrac{P}{2}=-1−\dfrac{1}{2}=−1.5\) and are spaced \(\dfrac{P}{4}=\dfrac{1}{4}=.25\) units apart. They are \(x= -1.5,\; -1.25,\; -1\;, -.75,\; -.5\).
• Step 4. Asymptotes, at the first and last quarter points, are \(x=-1.5\) and \(x=-0.5\)
• Step 5. \(D = -1\), so the vertical shift moves everything down 1 unit.
• Step 6. Coordinates of the middle three quarter points are \((−1.25, \; 1)\), \((−1, \; −1)\), and \((−0.75, \; −3)\). The graph is shown in Figure \(\PageIndex{2}\).
• The domain is \( \{x \; | \;  x≠ -\dfrac{1}{2}+ k \} \), where \(k\) is any integer. The range is \((−∞,∞)\).

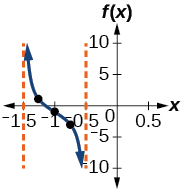
Figure \(\PageIndex{3}\) One period of the function \(y=−2\tan(\pi x+\pi)−1\).

 Try It \(\PageIndex{3}\)

How would the graph in Example \(\PageIndex{2}\) look different if we made \(A=2\) instead of \(−2\)?

Answer

It would be reflected across the line \(y=−1\), becoming an increasing function.

Construct an Equation for a Stretched or Compressed Tangent Function 

 Howto: Given the graph of a tangent function, identify horizontal and vertical stretches.

1. Find the period \(P\) from the spacing between successive vertical asymptotes or x-intercepts.
2. Write \(f(x)=A\tan \left (\dfrac{\pi}{P}x \right )\).
3. Determine a convenient point \((x,f(x))\) on the given graph and use it to determine \(A\).

Example \(\PageIndex{4}\): Identifying the Graph of a Stretched Tangent

Find a formula for the function graphed in Figure \(\PageIndex{4a}\). The graph goes through the point \( (2, \;2)\).

Figure \(\PageIndex{4a}\): A stretched tangent function

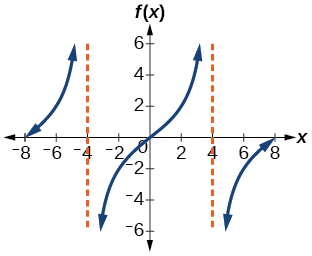
Solution

The graph has the shape of a tangent function.

• Step 1. One cycle extends from \(–4\) to \(4\), so the period is \(P=8\). Since \(P=\dfrac{\pi}{| B |}\), we have \(B=\dfrac{π}{P}=\dfrac{\pi}{8}\).
• Step 2. The equation must have the form \(f(x)=A\tan \left (\dfrac{\pi}{8}x \right )\).
• Step 3. To find the vertical stretch \(A\), we can use the point \((2,2)\): \( 2=A\tan \left (\dfrac{\pi}{8}\cdot 2 \right ) =A\tan \left (\dfrac{\pi}{4} \right )  = A\)

This function would have a formula \(f(x)=2\tan \left (\dfrac{\pi}{8}x \right )\).

 Try It \(\PageIndex{4}\)

Find a formula for the function in Figure \(\PageIndex{4b}\). (The point \(\left(\dfrac{\pi}{8}, 4 \right)\) is on the graph.)

Figure \(\PageIndex{4b}\)

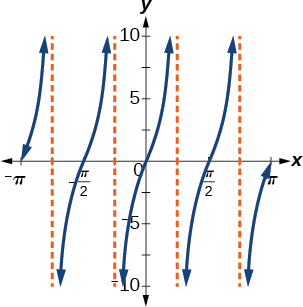
Answer

\(g(x)=4\tan(2x)\)

Analyzing the Graph of \(y = \cot x\)

The next trigonometric function we need to explore is cotangent. The cotangent is defined by the reciprocal identity \(\cot \, x=\dfrac{1}{\tan x}\). Notice that the function is undefined when the tangent function is \(0\), leading to a vertical asymptote in the graph at \(0\), \(\pi\), etc. Since the output of the tangent function is all real numbers, the output of the cotangent function is also all real numbers. Because the two functions are reciprocals of each other, when one graph is increasing, the other is decreasing.

The cotangent graph has vertical asymptotes at each value of \(x\) where \(\tan x=0\); we show these in the graph below with dashed lines. Since the cotangent is the reciprocal of the tangent, \(\cot x\) has vertical asymptotes at all values of \(x\) where \(\tan x=0\), and \(\cot x=0\) at all values of \(x\) where \(\tan x\) has its vertical asymptotes.

Figure \(\PageIndex{5}\): The cotangent function

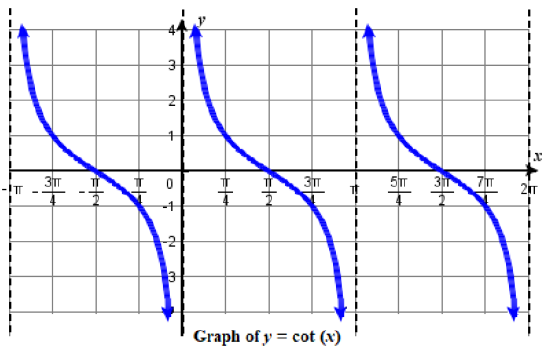
Graph a Stretched or Compressed Cotangent Function

FEATURES OF THE GRAPH OF \(y = A \cot(Bx)\)

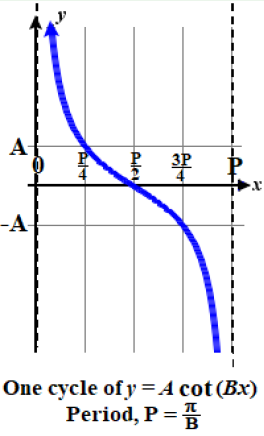• The vertical stretching factor \(|A|\).  There is no amplitude.
• The period is \(P=\dfrac{\pi}{|B|}\).
• The vertical asymptotes occur at \(x=P \cdot k\), where \(k\) is any integer and \(P\) is the period.
• The domain is all real numbers \(x\), where \( \{ x | x≠ P\cdot k \}\) where \(k\) is any integer and \(P\) is the period. 
• The range is \((−∞,∞)\).
• \(y=A\cot(Bx)\) is an odd function.

Figure \(\PageIndex{6a}\): Generic Graph for \(y = A \cot (Bx)\), with \(A\) and \(B\) both positive (or both negative)

As with the tangent function, these results can be confirmed by examining the start of a cycle of \(f(x) = =A \tan(Bx)\), and relating it to the the behaviour of the parent function \(y = cot (x)\).  A cycle for \(f\) starts when its argument \(Bx = 0\) and ends when \(Bx = \pi\). Solving these equations we obtain the cycle for \(f\) starts when \(x=0\), ends when \(x=\dfrac{\pi}{B}\), and consequently has a length (known as the period) of \(\dfrac{\pi}{B}\).

 Howto: Given a modified cotangent function of the form \(f(x)=A\cot(Bx)\), graph one period.

Rewrite the equation so that \(B\) is positive. Express the equation in the form \(f(x)=A \cot(Bx)\).

1. Identify the vertical stretching factor, \(|A|\). If \(A\) is negative, the graph will be a reflection over the \(x\)-axis and will increase over one cycle (rather than decrease).
2. Identify B and determine the period, \(P=\dfrac{\pi}{|B|}\).
3. Evaluate the \(x\) values for the five quarter points, starting at \(x=0\) and spaced \(\dfrac{P}{4}\) units apart.
4. Draw vertical asymptotes at the first and last quarter points, \(x=0\) and \(x = P\).
5. Evaluate the function at the middle three quarter points and draw the graph through these points.

In summary, quarter point values of \(x\) and corresponding values for \(f(x)=A \cot(|B|x)\) for one cycle are shown in the table below.

\( \begin{array}{|c|c||c|c| c |}
\hline
x = 0 & x = \dfrac{P}{4} & x = \dfrac{P}{2} & x = \dfrac{3P}{4} & x = P \\[4pt]
\hline
\text{asymptote} & y = A & y = 0 & y = -A & \text{asymptote}\\
\hline \end{array} \)

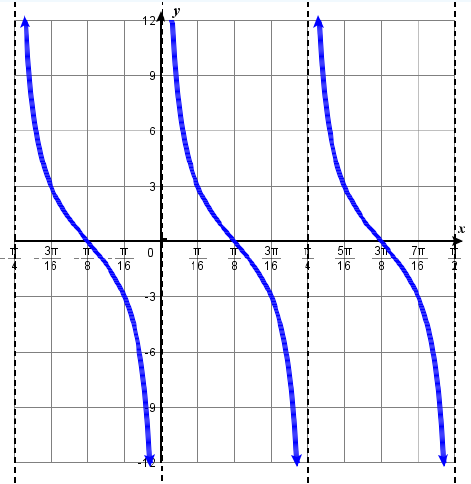
Example \(\PageIndex{6}\): Graphing Variations of the Cotangent Function

Determine the vertical stretching factor, period, and phase shift of \(y=3\cot(4x)\), and then sketch a graph. State the domain and range.

Solution

• The function is in the form \(f(x)=A\cot(Bx)\) gives \(f(x)=3\cot(4x)\).
• Step 1. \(A=3\). The vertical stretching factor is \(|A|=3\).
• Step 2. \(B=4\). The period is \(P=\dfrac{\pi}{|B|}=\dfrac{\pi}{4}\).
• Step 3. The five quarter points start at \(x=0\) and are spaced \(\dfrac{P}{4}=\dfrac{\dfrac{\pi}{4}}{4} = \dfrac{\pi}{16}\) units apart.  They are \(x= 0,\; \dfrac{\pi}{16},\; \dfrac{\pi}{8},\; \dfrac{3\pi}{16},\; \dfrac{\pi}{4}\).
• Step 4. Sketch the asymptotes at the first and last quarter points, \(x=0\), \(x=\dfrac{\pi}{4}\).
• Step 5. The coordinates of the three middle quarter points are \(\left (\dfrac{\pi}{16},3 \right )\),  \(\left (\dfrac{\pi}{8},0 \right )\), and \(\left (\dfrac{3\pi}{16},−3 \right )\)
• The domain is \( \{ x | x≠ \dfrac{\pi}{4} k \}\) where \(k\) is any integer; the range is \((−∞,∞)\).

Figure \(\PageIndex{6}\) Graph of three periods of \(y=3\cot(4x)\)

Graph a Vertically or Horizontally Shifted Cotangent Function

We can transform the graph of the cotangent in much the same way as we did for the tangent. The equation becomes  \(y=A\cot(Bx−C)+D\).

PROPERTIES OF THE GRAPH OF \(y = A \cot(Bx-C)+D\)

• The vertical stretching factor is \(| A |\). There is no amplitude.  
• The period is \(P = \dfrac{\pi}{|B|}\)
• The phase shift is \(H = \dfrac{C}{B}\) units (right when \(H\) is positive, left when \(H\) is negative).
• The vertical shift is \(D\) units (up when \(D\) is positive, down when \(D\) is negative).
• The vertical asymptotes occur at \(x = H + P \cdot k\), where \(k\) is any integer and \(P\) is the period.
• The domain is \(x≠H+P \cdot k\), where \(k\) is an integer, \(P\) is the period and \(H\) is the phase shift..
• The range is \((−∞,∞)\).

The graph of this transformed cotangent function is fundamentally the generic cotangent function \(y = A \cot (Bx)\), that has been shifted \(H\) units 'right' and \(D\) units 'up'. 

 Howto: Given a modified cotangent function of the form \(f(x)=A\cot(Bx−C)+D\), graph one period.

Rewrite the equation so that \(B\) is positive. Express the function in the form \(f(x)=A\cot(Bx−C)+D\).

1. Identify the vertical stretching factor, \(| A |\). If \(A\) is negative, the graph will be a reflection over the \(x\)-axis and will increase over one cycle (rather than decrease).
2. Identify \(B\) and determine the period, \(P=\dfrac{\pi}{|B|}\).
3. Identify \(C\) and determine the phase shift, \(H = \dfrac{C}{B}\).
4. Evaluate the \(x\) values for the five quarter points, starting at \(x=H\) and spaced \(\dfrac{P}{4}\) units apart.
5. Draw vertical asymptotes at at the first and last quarter points,  \(x=H\) and \(x = P+H\).
6. Identify \(D\), which is the vertical shift.
7. Evaluate the function at the middle three quarter points and draw the graph through these points. Notice that each of these points are the middle three points from the graph of \(y = A \cot (Bx)\), that have had \(H\) added to their \(x\) coordinates, and \(D\) added to their \(y\) coordinates.

In summary, quarter point values of \(x\) and corresponding values for \(g(x)=A \cot(|B|x-C)+D\) for one cycle are shown in the table below.

\( \begin{array}{|c|c||c|c| c |}
\hline
x = H & x = \dfrac{P}{4}+H & x = \dfrac{P}{2}+H & x = \dfrac{3P}{4}+H & x = P+H \\[4pt]
\hline
\text{asymptote} & y = A+D & y = D & y = -A+D & \text{asymptote}\\
\hline \end{array} \)

Example \(\PageIndex{7}\): Graphing a Modified Cotangent

Sketch a graph of one period of the function \(f(x)=4\cot \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).

Solution

Figure \(\PageIndex{7}\): One period of a modified cotangent function

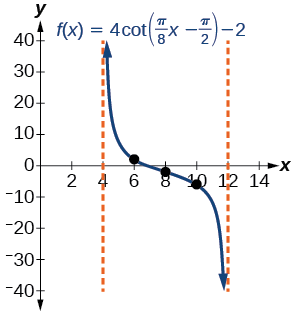
• The function is already written in the general form \(f(x)=A\cot(Bx−C)+D\).
• Step 1. \(A=4\), so the  vertical stretching factor is \(4\).
• Step 2. \(B=\dfrac{\pi}{8}\), so the period is \(P=\dfrac{\pi}{| B |}=\dfrac{\pi}{\dfrac{\pi}{8}}=8\).
• Step 3. \(C=\dfrac{\pi}{2}\), so the phase shift is \(H = \dfrac{C}{B}=\dfrac{\dfrac{\pi}{2}}{\dfrac{\pi}{8}}=4\).
• Step 4. The five quarter points start at \(x=4\) and are spaced \(\dfrac{P}{4} = \dfrac{8}{4}=2\) units apart. They are \(x= 4,\; 6,\; 8\;, 10,\; 12\).
• Step 4. Draw vertical asymptotes \(x=4\) and \(x=12\).
• Step 5. \(D=-2\), so the graph is shifted down two units.
• Step 6. The coordinates of the three middle quarter points are \((6,2)\), \((8,−2)\), and \((10,−6)\).
• The domain is \( \{x \; | \;  x≠ 4 + 8k \} \), where \(k\) is any integer. The range is \((−∞,∞)\).

The graph is shown in Figure \(\PageIndex{7}\).

 

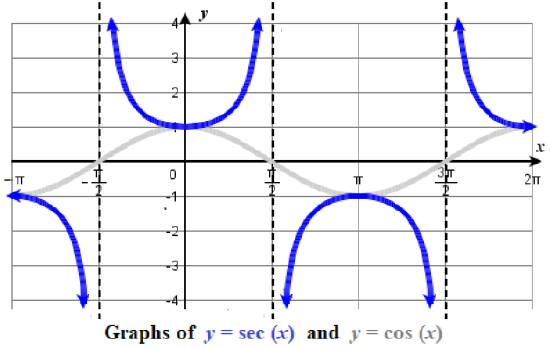
Analyzing the Graph of \(y = \sec x\)

For shifted, compressed, and/or stretched versions of the secant and cosecant functions, we can follow similar methods to those we used for tangent and cotangent. That is, we locate the vertical asymptotes and also evaluate the functions for a few points (specifically the local extrema). 

The secant was defined by the reciprocal identity \(sec \, x=\dfrac{1}{\cos x}\). Notice that the function is undefined when the cosine is \(0\), leading to vertical asymptotes at \(\dfrac{\pi}{2}\), \(\dfrac{3\pi}{2}\) etc. Because the cosine is never more than \(1\) in absolute value, the secant, being the reciprocal, will never be less than \(1\) in absolute value.

We can graph \(y=\sec x\) by observing the graph of the cosine function because these two functions are reciprocals of one another. See Figure \(\PageIndex{8}\). The graph of the cosine is shown as a grey curve so we can see the relationship. Where the graph of the cosine function decreases, the graph of the secant function increases. Where the graph of the cosine function increases, the graph of the secant function decreases. When the cosine function is zero, the secant is undefined.

The secant graph has vertical asymptotes at each value of \(x\) where the cosine graph crosses the \(x\)-axis; we show these in the graph below with dashed vertical lines.

Note that, because cosine is an even function, secant is also an even function. That is, \(\sec(−x)=\sec x\).

Figure \(\PageIndex{8}\): Graph of the secant function, \(f(x)=\sec x=\dfrac{1}{\cos x}\)

Graph a Stretched or Compressed Cotangent Function 

As we did for the tangent function, we will again refer to the constant \(| A |\) as the stretching factor, not the amplitude.

FEATURES OF THE GRAPH OF \(y = A \sec(Bx)\)

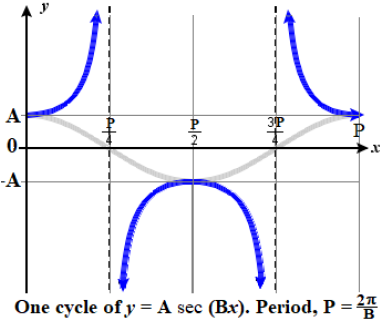• The vertical stretching factor is \(|A|\). There is no amplitude. 
• The period is \(P=\dfrac{2\pi}{| B |}\).
• The vertical asymptotes occur at \(x=\dfrac{P}{4}+\dfrac{P}{2} \cdot k\) where \(k\) is any integer and \(P\) is the period.
• The domain is \(\{ x \; | \; x≠\dfrac{P}{4}+\dfrac{P}{2} \cdot k \}\), where \(k\) is any integer and \(P\) is the period.
• The range is \((−∞,−|A|]∪[|A|,∞)\).
• \(y=A\sec(Bx)\) is an even function because cosine is an even function.

Figure \(\PageIndex{9a}\): Generic Graph for \(y = A \sec (Bx)\), with \(A\) positive

These results can be confirmed by examining the start of a cycle of \(f(x)= A \sec(Bx)\), and relating it to the the behaviour of the parent function \(y = \sec (x)\). A cycle for \(f\) starts when its argument \(Bx = 0\) and ends when \(Bx = 2\pi\). Solving these equations we obtain the cycle for \(f\) starts when \(x=0\), ends when \(x=\dfrac{2\pi}{B}\), and consequently has a length (known as the period) of \(\dfrac{2\pi}{B}\).

 Howto: Given a function of the form \(y=A\sec(Bx)\), graph one period

Rewrite the equation so that \(B\) is positive. Express the function given in the form \(y=A\sec(Bx)\).

1. Identify the vertical stretching factor, \(|A|\).  If \(A\) is negative, the graph will be a reflection over the \(x\)-axis.
2. Identify \(B\) and determine the period, \(P=\dfrac{2\pi}{| B |}\).
3. Evaluate the \(x\) values for the five quarter points, starting at \(x=0\) and spaced \(\dfrac{P}{4}\) units apart.
4. Draw vertical asymptotes for the secant function, \(x=\dfrac{P}{4}\) and \(x=\dfrac{3P}{4}\). These asymptotes are half a period apart at the second and fourth quarter points. These places are where the cosine function is zero.
5. Determine the location of local extrema which are also half a period apart - at the first, third and fifth quarter points when \(x=0\), \(x=\dfrac{P}{2}\) and \(x=P\). These are places where the cosine function is a maximum at the same time the secant is a minimum, and vice versa. Sketch the graph of \(y=A\sec(Bx)\).

In summary, quarter point values of \(x\) and corresponding values for \(f(x)=A \sec(|B|x)\) for one cycle are shown in the table below.

\( \begin{array}{|c|c||c|c| c |}
\hline
x = 0 & x = \dfrac{P}{4} & x = \dfrac{P}{2} & x = \dfrac{3P}{4} & x = P \\[4pt]
\hline
 y = A & \text{asymptote} & y = -A & \text{asymptote} & y = A\\
\hline \end{array} \)

Example \(\PageIndex{9}\): Graphing a Variation of the Secant Function

Graph one period of \(f(x)=3\sec(0.4x)\). State the domain and range of \(f\).

Solution

• The given function is already written in the general form, \(y=A\sec(Bx)\).
• Step 1. \(A=3\) so the vertical stretching factor is \(3\).
• Step 2. \(B=0.4\) so \(P=\dfrac{2\pi}{0.4}=5\pi\). The period is \(5\pi\) units. 
• Step 3. The five quarter points start at \(x=0\) and are \(\dfrac{P}{4}=\dfrac{5\pi}{4}\) units apart. They are \(x= 0,\; 1.25\pi,\; 2.5\pi\;, 3.75\pi,\; 5pi\).
• Step 4. Vertical asymptotes for the secant function (or places where the cosine function is zero), occur half a period apart at the second and fourth quarter points,  \(x=1.25\pi\) and \(x=3.75\pi\).
• Step 5. Extrema occur half a period apart at the first, third and fifth quarter points. The coordinates of these points are at \((0, \; 3)\), \((2.5\pi, \; -3)\), and \((5\pi, \; 3)\). Sketch the graph of the function \(f(x)=3\sec(0.4x)\) and if desired, its reciprocal function, \(g(x)=3\cos(0.4x)\).
• The domain is \(x≠\dfrac{5\pi}{4}+\dfrac{5\pi}{2} \cdot k\), where \(k\) is any integer. The range is \((−∞,−3]∪[3,∞)\).

Figure \(\PageIndex{9a}\) \(\color{Blue}{f(x)=3\sec(0.4x)}\) and \(\color{Grey}{g(x)=3\cos(0.4x)}\)

 Try It \(\PageIndex{9}\)

Graph one period of \(f(x)=−2.5\sec(0.4x)\).

Answer

This is a vertical reflection of the preceding graph because \(A\) is negative.

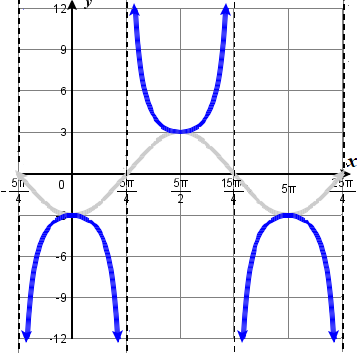
Figure \(\PageIndex{9b}\) \(\color{Blue}{f(x)=-3\sec(0.4x)}\) and \(\color{Grey}{g(x)=-3\cos(0.4x)}\)

Graph a Vertically or Horizontally Shifted Secant Function

Vertical shifts and (horizontal) phase shifts may be applied to the secant function in the same way as for the other functions. The general equation for secant is \(y=A\sec(Bx−C)+D \).

FEATURES OF THE GRAPH OF \(Y = A\sec(Bx−C)+D\)

• The vertical stretching factor is \(| A |\). There is no amplitude.
• The period is \(P = \dfrac{2\pi}{|B|}\).
• The phase shift is \(H = \dfrac{C}{B}\) units (right when \(H\) is positive, left when \(H\) is negative).
• The vertical shift is \(D\) units (up when \(D\) is positive, down when \(D\) is negative).
• The vertical asymptotes occur half a period apart at \(x= H + \dfrac{P}{4} + \dfrac{P}{2} \cdot k\), where \(k\) is any integer and \(P\) is the period.
• The domain is \(\{ x \; | \; x≠ H + \dfrac{P}{4}+\dfrac{P}{2} \cdot k \}\), where \(k\) is any integer and \(P\) is the period.
• The range is \((−∞,D−|A|]∪[D+|A|,∞)\).

The graph of this transformed secant function is fundamentally the generic secant function \(y = A \sec (Bx)\), that has been shifted \(H\) units 'right' and \(D\) units 'up'. 

 Do the vertical shift and stretch/compression affect the secant’s range?  

Yes. The range of \(f(x)=A\sec(Bx−C)+D\) is \((−∞,−|A|+D]∪[|A|+D,∞)\).

 Howto: Given a function of the form \(f(x)=A\sec(Bx−C)+D\), graph one period.

Rewrite the equation so that \(B\) is positive. Express the function in the form \(f(x)=A\sec(Bx−C)+D\).

1. Identify the vertical stretching factor, \(| A |\).  If \(A\) is negative, the graph will be a reflection over the \(x\)-axis.
2. Identify \(B\) and determine the period, \(P = \dfrac{2\pi}{|B|}\).
3. Identify \(C\) and determine the phase shift, \(H = \dfrac{C}{B}\). 
4. Evaluate the \(x\) values for the five quarter points, starting at \(x=H\) and spaced \(\dfrac{P}{4}\) units apart.
5. Vertical asymptotes are at the second and fourth quarter points which are \(x=H + \dfrac{P}{4}\) and \(x=H + \dfrac{3P}{4}\)
6. Identify \(D\), which is the vertical shift. 
7. Evaluate the function where local extrema exist, which occur at the first, third and fifth quarter points, and draw the graph through these points. Notice that this is the same graph that would be obtained by graphing \(y=A \sec(Bx)\), but shifting it to the right/left by \(H\) units and up/down by \(D\) units.
   Local extrema are at \( (H, \; D+A) \), \( (H + \dfrac{P}{2}, \; D-A) \), and \( (H + P, \; D+A) \), 

In summary, quarter point values of \(x\) and corresponding values for \(g(x)=A \sec(|B|x-C)+D\) for one cycle are shown in the table below.

\( \begin{array}{|c|c||c|c| c |}
\hline
x = H & x = \dfrac{P}{4}+H & x = \dfrac{P}{2}+H & x = \dfrac{3P}{4}+H & x = P+H \\[4pt]
\hline
y = A+D & \text{asymptote} & y = -A+D & \text{asymptote} & y = A+D  \\
\hline \end{array} \)

 Try It \(\PageIndex{10}\)

Given the graph of \(f(x)=2\cos \left (\dfrac{\pi}{2}x \right )+1\) shown in Figure \(\PageIndex{10a}\), sketch the graph of \(g(x)=2\sec \left (\dfrac{\pi}{2}x \right )+1\) on the same axes.

Figure \(\PageIndex{10a}\)

Answer

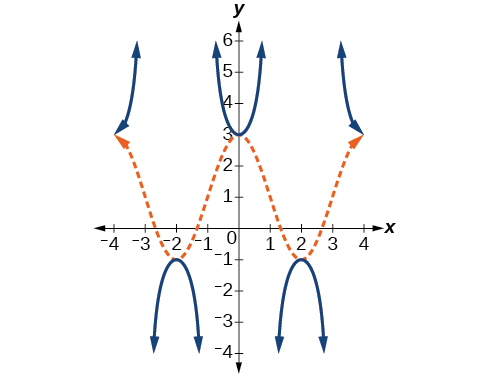
Figure \(\PageIndex{10b}\)

 

 Example \(\PageIndex{11}\): Graphing a Variation of the Secant Function

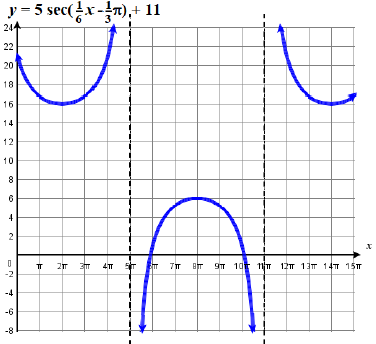
Graph one period of \(f(x) = 5 \sec \left( \dfrac{x}{6} - \dfrac{\pi}{3} \right) +11\). State the domain and range.

Solution

• The function parameters are \(A=5\), \(B=\dfrac{1}{6}\), \(C = \dfrac{\pi}{3}\), and \(D = 11\).
• Step 1. The vertical stretching factor is \(| A |= 5\).
• Step 2. The period is \( P = \dfrac{2\pi}{|B|}= \dfrac{2\pi}{\dfrac{1}{6}}= 2\pi \cdot \dfrac{6}{1}= 12\pi \). 
• Step 3. The phase shift is \(H = \dfrac{C}{B}= \dfrac{\dfrac{\pi}{3}}{\dfrac{1}{6}}= \dfrac{\pi}{3}\cdot \dfrac{6}{1}= 2\pi \). 
• Step 4. The quarter points starting at \(H=2\pi\) and \(\dfrac{P}{4}=\dfrac{12\pi}{4}=3\pi\) units apart are \(x= 2\pi,\; 5\pi,\; 8\pi\;, 11\pi,\; 14\pi\).
• Step 5. Vertical asymptotes, at the second and fourth quarter points, are \(x=5\pi\) and \(x = 11\pi\).
• Step 6. The vertical shift is \(D=11\) or up one unit.
• Step 7. Coordinates of the extrema, at the first, third and fifth quarter points, are \((2\pi, f(2\pi)=A+D=16)\), \((8\pi,\; 6)\), and \((14\pi,\; 16)\). Figure \(\PageIndex{12}\) shows a graph. 
• The domain is \(\{ x \; | \; x≠ 5\pi + 6\pi \cdot k \}\), where \(k\) is any integer. The range is \((−∞,6]∪[16,∞)\).

 

Figure \(\PageIndex{11}\) Graph of \(y = 5 \sec \left( \dfrac{x}{6} - \dfrac{\pi}{3} \right) +11\)

 Try It \(\PageIndex{11}\)

Graph one period of \(f(x)=4\sec \left( -\dfrac{\pi}{8}x -\dfrac{3\pi}{8} \right) - 8\). State the domain and range.

Answer

\( (f(x)=4\sec\left( \dfrac{\pi}{8}x+\dfrac{3\pi}{8} \right) - 8\). (Rewritten because \(B\) initially was negative). Parameters are \(A=4\), \(B=\dfrac{\pi}{8}\), \(C = -\dfrac{3\pi}{8}\), and \(D = -8\). Period \(P=16\), Phase shift \(H=-3\). The domain is \(\{ x \; | \; x≠ 1 + 8k \}\), where \(k\) is any integer. The range is \((−∞,-12]∪[-4,∞) \) 

Figure \(\PageIndex{11}\) Graph of \(f(x)=4\sec \left( -\dfrac{\pi}{8}x -\dfrac{3\pi}{8} \right) - 8\)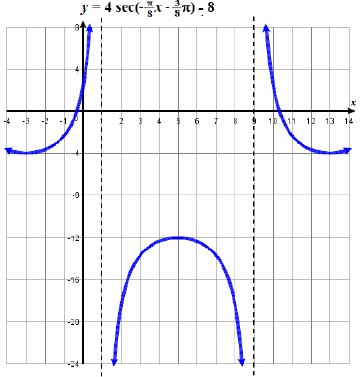

Analyzing the Graph of \(y = \csc x\)

Similar to the secant, the cosecant is defined by the reciprocal identity \(\csc x=\dfrac{1}{\sin x}\). Notice that the function is undefined when the sine is \(0\), leading to a vertical asymptote in the graph at \(0\), \(\pi\), etc. Since the sine is never more than \(1\) in absolute value, the cosecant, being the reciprocal, will never be less than \(1\) in absolute value.

We can graph \(y=\csc x\) by observing the graph of the sine function because these two functions are reciprocals of one another. See Figure \(\PageIndex{7}\). The graph of sine is shown as a grey curve so we can see the relationship. Where the graph of the sine function decreases, the graph of the cosecant function increases. Where the graph of the sine function increases, the graph of the cosecant function decreases.

The cosecant graph has vertical asymptotes at each value of \(x\) where the sine graph crosses the \(x\)-axis; we show these in the graph below with dashed vertical lines.

Note that, since sine is an odd function, the cosecant function is also an odd function. That is, \(\csc(−x)=−\csc x\).

The graph of cosecant, which is shown in Figure \(\PageIndex{9}\), is similar to the graph of secant.

Figure \(\PageIndex{12}\): The graph of the cosecant function, \(f(x)=\csc x\), and its reciprocal function \(g(x) = sin(x)\).

Graph a Stretched or Compressed Cosecant Function

FEATURES OF THE GRAPH OF \(y = A \csc(Bx)\)

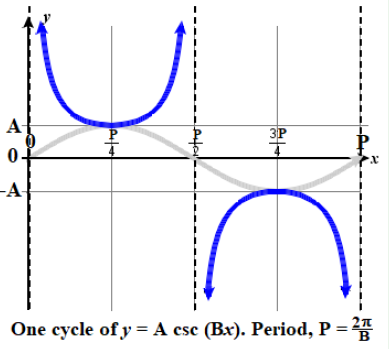• The vertical stretching factor is \(| A |\).  There is no amplitude. 
• The period is \(\dfrac{2\pi}{|B|}\).
• The vertical asymptotes occur at \(x=P \cdot k\), where \(k\) is any integer and \(P\) is the period.
• The domain is \(\{ x \; | \; x≠P \cdot k\), where \(k\) is any integer and \(P\) is the period.
• The range is \((−∞,−|A|]∪[|A|,∞)\).
• \(y=A\csc(Bx)\) is an odd function because sine is an odd function.

Figure \(\PageIndex{13a}\): Generic Graph for \(y = A \csc (Bx)\), with \(A\) and \(B\) both positive

These results can be confirmed by examining the start of a cycle of \(f(x) = A \csc(Bx)\), and relating it to the the behaviour of the parent function \(y = \csc (x)\).  A cycle for \(f\) starts when its argument \(Bx = 0\) and ends when \(Bx = 2\pi\). Solving these equations we obtain the cycle for \(f\) starts when \(x=0\), ends when \(x=\dfrac{2\pi}{B}\), and consequently has a length (known as the period) of \(\dfrac{2\pi}{B}\).

 Howto: Given a function of the form \(y=A\csc(Bx)\), graph one period.

Rewrite the equation so that \(B\) is positive. Express the function given in the form \(y=A\csc(Bx)\).

1. Identify the vertical stretching factor, \(|A|\).  If \(A\) is negative, the graph will be a reflection over the \(x\)-axis.
2. Identify \(B\) and determine the period, \(P=\dfrac{2\pi}{| B |}\).
3. Evaluate the \(x\) values for the five quarter points, starting at \(x=0\) and spaced \(\dfrac{P}{4}\) units apart.
4. Draw vertical asymptotes for one period of the cosecant function, \(x=0\),  \(x=\dfrac{P}{2}\) and \(x=P\). The asymptotes are half a period apart, at the first, third and fifth quarter points. These places are where the sine function is zero.
5. Determine the location of local extrema which are also half a period apart - at the second and fourth quarter points when \(x=\dfrac{P}{4}\) and \(x=\dfrac{3P}{4}\). These are places where the sine function is a maximum at the same time the cosecant is a minimum, and vice versa. Sketch the graph of \(y=A\csc(Bx)\).

In summary, quarter point values of \(x\) and corresponding values for \(f(x)=A \csc(|B|x)\) for one cycle are shown in the table below.

\( \begin{array}{|c|c||c|c| c |}
\hline
x = 0 & x = \dfrac{P}{4} & x = \dfrac{P}{2} & x = \dfrac{3P}{4} & x = P \\[4pt]
\hline
 \text{asymptote} & y = A & \text{asymptote} & y = -A & \text{asymptote} \\
\hline \end{array} \)

Example \(\PageIndex{13}\): Graphing a Variation of the Cosecant Function

Graph one period of \(f(x)=−3\csc(4x)\). State the domain and range.

Solution

• Parameters are \(A=-3\), \(B=4\).
• Step 1. \(| A |=| −3 |=3\), so the vertical stretching factor is \(3\).
• Step 2. \(B=4\), so \(P=\dfrac{2\pi}{4}=\dfrac{\pi}{2}\). The period is \(P = \dfrac{\pi}{2}\) units.
• Step 3. The five quarter points, starting at \(x=0\) and spaced \( \dfrac{\pi}{8}\) units apart, are \(x= 0,\; \dfrac{\pi}{8},\; \dfrac{\pi}{4},\; \dfrac{3\pi}{8},\; \dfrac{\pi}{2}\).
• Step 4. Sketch three asymptotes at \(x=0\), \(x=\dfrac{\pi}{4}\), and \(x=\dfrac{\pi}{2}\).
• Step 5. Coordinates of the extrema are \(\left (\dfrac{\pi}{8},−3 \right )\) and  \(\left (\dfrac{3\pi}{8},3 \right )\).
• Figure \(\PageIndex{14}\) shows the graph.  Domain is \(\{ x \; | \; x≠\dfrac{\pi}{4} \cdot k\), where \(k\) is any integer. The range is \((−∞,−3]∪[3,∞)\).

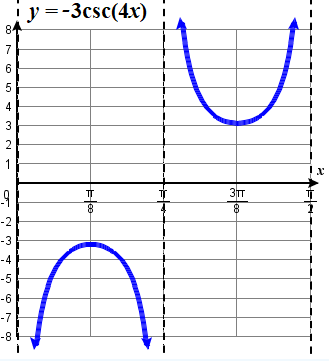
Figure \(\PageIndex{13b}\) Graph of one period of \(f(x)=−3\csc(4x)\).

 Try It \(\PageIndex{13}\)

Graph one period of \(f(x)=0.5\csc(2\pi x)\).

Answer

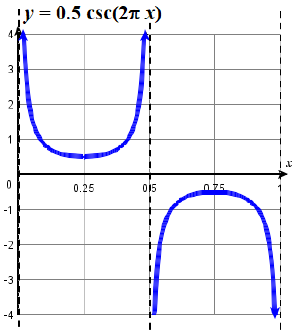
Figure \(\PageIndex{13c}\). Graph of one period of \(f(x)=0.5\csc(2\pi x)\).

Graph a Vertically or Horizontally Shifted Cosecant Function 

Vertical and phase shifts may be applied to the cosecant function in the same way as for the secant and other functions.The equation for cosecant becomes \(y=A\csc(Bx−C)+D \)

FEATURES OF THE GRAPH OF \(Y = A\csc(Bx−C)+D\)

• The vertical stretching factor is \(|A|\).  There is no amplitude.
• The period is \(P = \dfrac{2\pi}{|B|}\).
• The phase shift is \(H = \dfrac{C}{B}\) units (right when \(H\) is positive, left when \(H\) is negative).
• The vertical shift is \(D\) units (up when \(D\) is positive, down when \(D\) is negative).
• The vertical asymptotes occur half a period apart at \(x= H + \dfrac{P}{2} \cdot k\), where \(k\) is any integer and \(P\) is the period.
• The domain is \(\{ x \; | \; x≠H+\dfrac{P}{2} \cdot k \} \), where \(k\) is any integer, \(P\) is the period, and \(H\) is the phase shift.
• The range is \ \((−∞,D−|A|]∪[D+|A|,∞)\).

The graph of this transformed secant function is fundamentally the generic secant function \(y = A \sec (Bx)\), that has been shifted \(H\) units 'right' and \(D\) units 'up'.   

 The domain of \(\csc \, x\) was given to be all \(x\) such that \(x≠k\pi\) for any integer \(k\). Would the domain of \(y=A\csc(Bx−C)+D\) be \(x≠\dfrac{C+k\pi}{B}\)?  

Yes. The excluded points of the domain follow the vertical asymptotes. Their locations show the horizontal shift and compression or expansion implied by the transformation to the original function’s input.

 Howto: Given a function of the form \(f(x)=A \csc(Bx−C)+D\), graph one period

Rewrite the equation so that \(B\) is positive. Express the function given in the form \(y=A\csc(Bx−C)+D\).

1. Identify the vertical stretching factor, \(|A|\).   If \(A\) is negative, the graph will be a reflection over the \(x\)-axis.
2. Identify \(B\) and determine the period, \(P = \dfrac{2\pi}{| B |}\).
3. Identify \(C\) and determine the phase shift, \(H = \dfrac{C}{B}\).   (Shift right when \(H\) is positive, left when \(H\) is negative).
4. Evaluate the \(x\) values for the five quarter points, starting at \(x=H\) and spaced \(\dfrac{P}{4}\) units apart.
5. Draw vertical asymptotes \(x=H\),  \(x=\dfrac{P}{2}+H\) and \(x=P+H\) . The asymptotes are half a period apart, at the first, third and fifth quarter points. These places are where the sine function is zero.
6. Identify \(D\), which is the vertical shift. (Shift up when \(D\) is positive, down when \(D\) is negative).
7. Evaluate the coordinates for the local extrema located at the second and fourth quarter points. These are places where the sine function is a maximum at the same time the cosecant is a minimum, and vice versa. Sketch the graph of \(y=A\csc(Bx−C)+D\).

In summary, quarter point values of \(x\) and corresponding values for \(f(x)=A \csc(|B|x-C)+D\) for one cycle are shown in the table below.

\( \begin{array}{|c|c||c|c| c |}
\hline
x = H & x = \dfrac{P}{4}+H & x = \dfrac{P}{2}+H & x = \dfrac{3P}{4}+H & x = P+H \\[4pt]
\hline
 \text{asymptote} & y = A+D & \text{asymptote} & y = -A+D & \text{asymptote} \\
\hline \end{array} \)

Example \(\PageIndex{14}\): Graphing a Vertically Stretched, Horizontally Compressed, and Vertically Shifted Cosecant

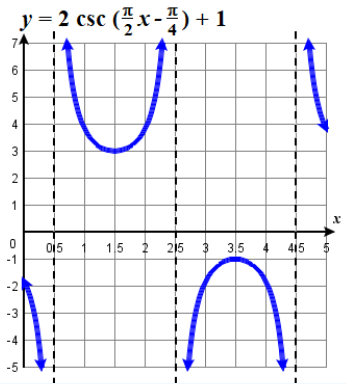
Sketch a graph of \(y = 2 \csc \left( \dfrac{\pi}{2} - \dfrac{\pi}{4} \right) + 1 \). State the domain and range.

Solution

• Parameters are \(A=2\), \(B=\dfrac{\pi}{2}\), \(C = \dfrac{\pi}{4}\), and \(D = 1\).
• Step 1. Vertical stretching factor is \(| A |=2\).
• Step 2. The period is \(\dfrac{2\pi}{| B |}=\dfrac{2\pi}{\dfrac{\pi}{2}}=2\pi⋅\dfrac{2}{\pi}\). So \(P = 4\)
• Step 3. The phase shift is \(\dfrac{\dfrac{\pi}{4}}{\dfrac{\pi}{2}}=\dfrac{1}{2}\). So \(H = 0.5\)
• Step 4. quarter points, starting at \(x=.5\) and spaced \(1\) unit apart, are \(x= 0.5,\; 1.5,\; 2.5\;, 3.5,\; 4.5\).
• Step 5. Vertical asymptotes are \(x=0.5\), \(x=2.5\), \(x=4.5\).
• Step 6. Draw the graph of \(y=A\csc(Bx)\) but shift it up \(D=1\).
• Step 7. Coordinates of extrema are \( (1.5,\; 3)\) and \((3.5,\; -3)\).
• Domain is \(\{ x \; | \; x≠0.5+2 k \} \), where \(k\) is any integer, domain is \((−∞,−1]∪[3,∞)\).

The graph for this function is shown in Figure \(\PageIndex{14a}\).

Figure \(\PageIndex{14a}\): Graph of \(y = 2 \csc \left( \dfrac{\pi}{2} - \dfrac{\pi}{4} \right) + 1 \)

 Try It \(\PageIndex{14}\)

Graph the function \(y = -3 \csc \left( -\dfrac{x}{3} + \dfrac{\pi}{6} \right) -5 \). State the domain and range. 

Answer

Function rewrite necessary: \(y = 3 \csc \left( \dfrac{x}{3} - \dfrac{\pi}{6} \right) -5 \). Parameters are \(A=3\), \(B=\dfrac{1}{3}\), \(C = \dfrac{\pi}{6}\), and \(D = -5\). \(P = 6\pi\). \(H= \dfrac{\pi}{2}\). Domain is \(\{ x \; | \; x≠\dfrac{\pi}{2}+3\pi k \} \), where \(k\) is any integer, domain is \((−∞,−8]∪[-2,∞)\).

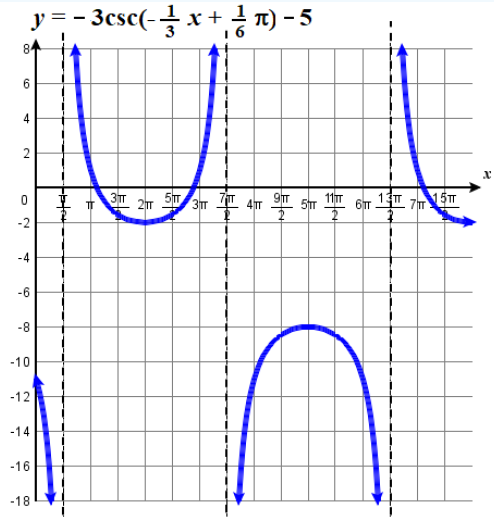
Figure \(\PageIndex{14b}\): Graph of the function \(y = -3 \csc \left( -\dfrac{x}{3} + \dfrac{\pi}{6} \right) -5 \).

Using the Graphs of Trigonometric Functions to Solve Real-World Problems

Many real-world scenarios represent periodic functions and may be modeled by trigonometric functions. As an example, let’s return to the scenario from the section opener. Have you ever observed the beam formed by the rotating light on a police car and wondered about the movement of the light beam itself across the wall? The periodic behavior of the distance the light shines as a function of time is obvious, but how do we determine the distance? We can use the tangent function.

Example \(\PageIndex{15}\): Using Trigonometric Functions to Solve Real-World Scenarios

Suppose the function \(y=5\tan(\dfrac{\pi}{4}t)\) marks the distance in the movement of a light beam from the top of a police car across a wall where \(t\) is the time in seconds and \(y\) is the distance in feet from a point on the wall directly across from the police car.

1. Find and interpret the vertical stretching factor and period.
2. Graph on the interval \([0,5]\).
3. Evaluate \(f(1)\) and discuss the function’s value at that input.

Solution

1. We know from the general form of \(y=A\tan(Bt)\) that \(| A |\) is the vertical stretching factor and \(\dfrac{\pi}{B}\) is the period.

Figure \(\PageIndex{15a}\)

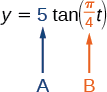
We see that the vertical stretching factor is \(5\). This means that the beam of light will have moved \(5\) ft after 1 second.

The period is \(\dfrac{\pi}{\tfrac{\pi}{4}}=\dfrac{\pi}{1}⋅\dfrac{4}{\pi}=4\). This means that every \(4\) seconds, the beam of light sweeps the wall. The distance from the spot across from the police car grows larger as the police car approaches.

2. To graph the function, we draw an asymptote at \(t=2\) and use the vertical stretching factor and period. See Figure \(\PageIndex{23}\)

Figure \(\PageIndex{15b}\)

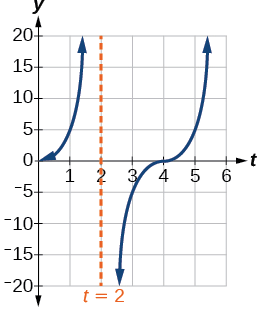
3. period: \(f(1)=5\tan(\frac{\pi}{4}(1))=5(1)=5\); after \(1\) second, the beam of has moved \(5\) ft from the spot across from the police car.

Media

Access these online resources for additional instruction and practice with graphs of other trigonometric functions.

• Graphing the Tangent
• Graphing Cosecant and Secant
• Graphing the Cotangent

Key Equations

Shifted, compressed, and/or stretched tangent function	\(y=A \tan(Bx−C)+D\)
Shifted, compressed, and/or stretched secant function	\(y=A \sec(Bx−C)+D\)
Shifted, compressed, and/or stretched cosecant function	\(y=A \csc(Bx−C)+D\)
Shifted, compressed, and/or stretched cotangent function	\(y=A \cot(Bx−C)+D\)

Key Concepts

• The tangent function has period \(π\).
• \(f( x )=A\tan( Bx−C )+D\) is a tangent with vertical and/or horizontal stretch/compression and shift. 
• The secant and cosecant are both periodic functions with a period of \(2\pi\). \(f( x )=A\sec( Bx−C )+D\) gives a shifted, compressed, and/or stretched secant function graph. 
• \(f( x )=A\csc( Bx−C )+D\) gives a shifted, compressed, and/or stretched cosecant function graph. 
• The cotangent function has period \(\pi\) and vertical asymptotes at \(0,±\pi,±2\pi\),....
• The range of cotangent is \(( −∞,∞ )\), and the function is decreasing at each point in its range.
• The cotangent is zero at \(±\dfrac{\pi}{2},±\dfrac{3\pi}{2}\),....
• \(f(x)=A\cot(Bx−C)+D\) is a cotangent with vertical and/or horizontal stretch/compression and shift. 
• Real-world scenarios can be solved using graphs of trigonometric functions. 

Contributors and Attributions

• Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.