5.5e: Exercises - Graphs of Sine and Cosine Functions

A: Concepts 

Exercise \(\PageIndex{A}\)

1. Why are the sine and cosine functions called periodic functions?

2. How does the graph of \(y=\sin x\) compare with the graph of \(y=\cos x\)?  Explain how you could horizontally translate the graph of \(y=\sin x\) to obtain \(y=\cos x\).

3. For the equation \(A \cos(Bx+C)+D\)$,$what constants affect the range of the function and how do they affect the range?

4. How does the range of a translated sine function relate to the equation \(y=A \sin(Bx+C)+D\)$?$

5. How can the unit circle be used to construct the graph of \(f(t)=\sin t\)?

Answers to odd-numbered problems:

1. The sine and cosine functions have the property that \(f(x+P)=f(x)\) for a certain \(P\). This means that the function values repeat for every \(P\) units on the \(x\)-axis.
3. The absolute value of the constant \(A\) (amplitude) increases the total range and the constant \(D\) (vertical shift) shifts the graph vertically.
5. At the point where the terminal side of \(t\) intersects the unit circle, you can determine that the \(\sin t\) equals the \(y\)-coordinate of the point.

B1: Identify Attributes and Graph non-phase-shifted sine equations 

Exercise \(\PageIndex{B1}\)

\( \bigstar \) For the following exercises, (a) State the amplitude and midline, (b) the period, and (c) the maximum and minimum \(y\)-values and their corresponding \(x\)-values on one period and (d) Graph two full periods of each function. Give exact answers (fractions and multiples of pi, rather than decimal approximations).

11. \(f(x) = \sin \left(   5x \right) +2  \\[4pt]  \)  12. \(f(x) = 4 \sin \left(  2 x \right) -1 \\[4pt] \)  13. \(f(x)=4\sin x \\[4pt] \) 14. \(f(x)=3\sin x +2 \\[4pt] \) 15. \(f(x) = 2\sin \left(  6 \pi x \right) +3 \\[4pt] \) 16. \(f(x) = 4\sin \left(  3 \pi x \right) +1  \)

17. \(f(x)=-3\sin x \\[4pt] \) 18. \(f(x)=-2\sin (4x) -2 \\[4pt] \) 18.1 \(f(x)=2\sin (-4x) -2 \\[4pt] \) 19. \(f(x) = 3\sin \left(  \dfrac{5}{4} x \right) +1 \\[2pt] \)  20. \(f(x) = \sin \left(    \dfrac{4}{5} x \right) \)

21. \(f(x)=2 \sin \left(\dfrac{1}{2}x\right)\\[2pt] \) 22. \(f(x) = \sin \left( \dfrac{2}{5}  x \right) -4\\[2pt] \)  23. \(f(x) = \sin \left( \dfrac{1}{6}  x \right) +3\\[2pt]  \)  24. \(f(x) = 4\sin \left(  \dfrac{5\pi}{2} x \right)  \)

25. \(f(x) = \sin \left( \dfrac{4\pi}{3}   x \right) -3\\[2pt] \) 26. \(f(x) = 3\sin \left(  \dfrac{3\pi}{4}  x \right) -1 \\[2pt] \) 27. \(f(x) = 3\sin \left( \dfrac{\pi}{2}  x \right) \\[2pt] \) 28. \(f(x) = 2\sin \left( \dfrac{\pi}{5}  x \right) -1 \)

Answers to odd numbered problems

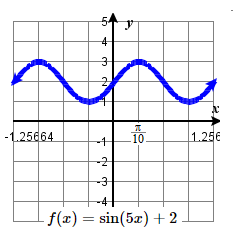11. amplitude: \(  1  \); period: \(  \frac{2\pi}{5}   \) midline: \(y= 2   \);
 \(\quad\) maximum: \(y= 3   \) occurs at \(x=\frac{1\pi}{10} \);
 \(\quad\) minimum: \(y=  1   \) occurs at \(x= \frac{3\pi}{10}   \);
 \(\quad\) one period starts at \(0\) and ends at \(  \frac{2\pi}{5}    \).

13. amplitude: \(  4  \); period: \(  2 \pi   \) midline: \(y= 0   \);
 \(\quad\) maximum: \(y=  4  \) occurs at \(x=\frac{1\pi}{2}\);
 \(\quad\) minimum: \(y=  -4   \) occurs at \(x=  \frac{3\pi}{2}  \);
 \(\quad\) one period starts at \(0\) and ends at \(  2 \pi   \).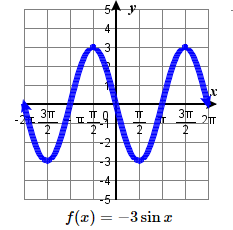

 

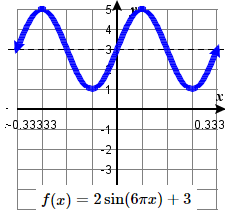15. amplitude: \(  2  \); period: \(   \frac{1}{3}  \) midline: \(y= 3   \);
 \(\quad\) maximum: \(y=  5  \) occurs at \(x=\frac{1}{12}\);
 \(\quad\) minimum: \(y=  1   \) occurs at \(x=  \frac{1}{4}  \);
 \(\quad\) one period starts at \(0\) and ends at \(  \frac{1}{3}   \).

17. amplitude: \(  3  \); period: \(   2 \pi  \) midline: \(y= 0   \);
 \(\quad\) maximum: \(y= 3   \) occurs at \(x=\frac{3\pi}{2}\);
 \(\quad\) minimum: \(y=  -3   \) occurs at \(x=  \frac{\pi}{2}  \);
 \(\quad\) one period starts at \(0\) and ends at \(  2 \pi   \).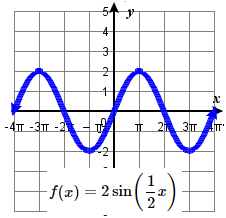

 

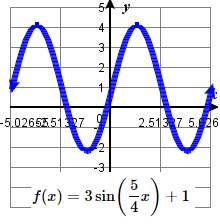19. amplitude: \(  3  \); period: \(   \frac{8\pi}{5}  \) midline: \(y=  1  \);
 \(\quad\) maximum: \(y= 4   \) occurs at \(x=\frac{2\pi}{5}\);
 \(\quad\) minimum: \(y=  -2   \) occurs at \(x=  \frac{6\pi}{5}  \);
 \(\quad\) one period starts at \(0\) and ends at \(  \frac{8\pi}{5}    \).

21. amplitude: \(  2  \); period: \(   4\pi  \) midline: \(y=  0  \);
 \(\quad\) maximum: \(y=  2  \) occurs at \(x=\pi\);
 \(\quad\) minimum: \(y=   -2  \) occurs at \(x= 3 \pi  \);
 \(\quad\) one period starts at \(0\) and ends at \(  4  \pi \).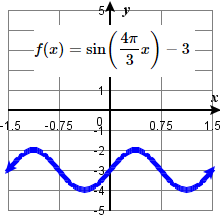

 

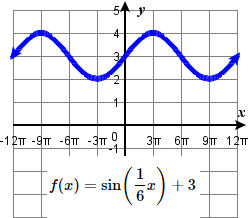23. amplitude: \(  1  \); period: \(   12\pi  \) midline: \(y=  3  \);
 \(\quad\) maximum: \(y= 4   \) occurs at \(x=3\pi\);
 \(\quad\) minimum: \(y= 2    \) occurs at \(x=  9 \pi \);
 \(\quad\) one period starts at \(0\) and ends at \(  12\pi   \).

25. amplitude: \(   1 \); period: \(   \frac{3}{2}  \) midline: \(y=  -3  \);
 \(\quad\) maximum: \(y= -2   \) occurs at \(x=\frac{3}{8}\);
 \(\quad\) minimum: \(y=  -4   \) occurs at \(x= \frac{9}{8}   \);
 \(\quad\) one period starts at \(0\) and ends at \(   \frac{3}{2}  \).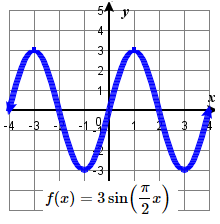

 

27. amplitude: \( 3 \); period: \(  4 \) midline: \(y= 0 \);
 \(\quad\) maximum: \(y= 3   \) occurs at \(x=1\);
 \(\quad\) minimum: \(y= -3    \) occurs at \(x=  3  \);
 \(\quad\) one period starts at \(0\) and ends at \(  4   \).

 

 

 

 

 

B2: Identify Attributes and Graph non-phase-shifted cosine equations

Exercise \(\PageIndex{B2}\)

\( \bigstar \) For the following exercises, (a) State the amplitude and midline, (b) the period, and (c) the maximum and minimum \(y\)-values and their corresponding \(x\)-values on one period and (d) Graph two full periods of each function. Give exact answers (fractions and multiples of pi, rather than decimal approximations).

31. \(f(x) = 3\cos (  3 x ) +2 \\[4pt] \) 32. \(f(x)=\cos (2x) \\[4pt] \) 33. \(f(x)=2\cos x \\[4pt] \) 34. \(f(x)=-3\cos x +1\\[4pt] \) 35. \(f(x)=2 \cos(\pi x) -3 \\[4pt] \) 36. \(f(x) = \cos \left(   4\pi x \right)\)

37. \(f(x)=-\cos (2 \pi x) -3\\[4pt] \) 38. \(f(x)=-\cos (6x) + 3 \\[4pt] \) 38.1 \(f(x)=\cos (-6x) + 3 \\[4pt] \) 39. \(f(x)=3 \cos\left(\dfrac{6}{5}x\right)\\[2pt]\) 40. \(f(x) = \cos \left( \dfrac{3}{2}  x \right) -2 \\[2pt]\)

41. \(f(x) = \cos \left(  \dfrac{5}{6} x \right) +1 \) 42. \(f(x) = 2\cos \left(  \dfrac{3}{5} x \right) \\[2pt]\) 43. \(f(x) =4 \cos \left( \dfrac{1}{3}  x \right) +1\\[2pt] \) 44.  \(f(x) = 2\cos \left( \dfrac{1}{4}  x \right) -2\\[2pt]\) 45. \(f(x) = 5\cos \left(  \dfrac{5 \pi}{3}  x \right) \)

46. \(f(x) = 2\cos \left( \dfrac{6 \pi}{5 }    x \right)+2 \\[2pt]\)  47. \(f(x) = 2\cos \left(  \dfrac{4\pi}{5}  x \right) +3\\[2pt]\)  48. \(f(x) = \cos \left(  \dfrac{3\pi}{4}  x \right) +2\\[2pt]\)  49. \(f(x) = \cos \left( \dfrac{2 \pi}{3 }   x \right) -1\)

Answers to odd numbered problems:

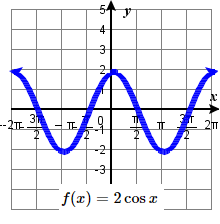
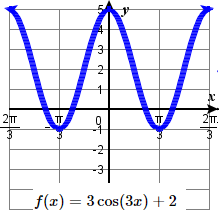31. amplitude: \(  3  \); period: \(  \frac{2\pi}{3}   \) midline: \(y= 2   \);
 \(\quad\) maximum: \(y= 5   \) occurs at \(x=0\);
 \(\quad\) minimum: \(y= -1    \) occurs at \(x= \frac{1\pi}{3}   \);
 \(\quad\) one period starts at \(0\) and ends at \(  \frac{2\pi}{3}   \).

33. amplitude: \(  2  \); period: \(  2 \pi   \) midline: \(y= 0   \);
 \(\quad\) maximum: \(y=  2  \) occurs at \(x=0\);
 \(\quad\) minimum: \(y=  -2   \) occurs at \(x=   \pi  \);
 \(\quad\) one period starts at \(0\) and ends at \(   2 \pi  \).

 

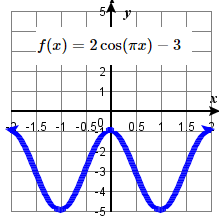35. amplitude: \( 2  \); period: \(   2  \) midline: \(y=  -3  \);
 \(\quad\) maximum: \(y= -1   \) occurs at \(x=0\);
 \(\quad\) minimum: \(y=  -5   \) occurs at \(x= 1   \);
 \(\quad\) one period starts at \(0\) and ends at \(  2   \).

37. amplitude: \(  1  \); period: \(    1 \) midline: \(y=  -3 \);
 \(\quad\) maximum: \(y=  -2  \) occurs at \(x=\frac{1}{2}\);
 \(\quad\) minimum: \(y=  -4   \) occurs at \(x= 0 \);
 \(\quad\) one period starts at \(0\) and ends at \(    1  \).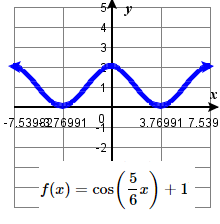

     

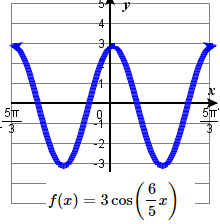39. amplitude: \(  3  \); period: \(   \frac{5\pi}{3}  \) midline: \(y=  0  \);
 \(\quad\) maximum: \(y= 3   \) occurs at \(x=0\);
 \(\quad\) minimum: \(y=   -3  \) occurs at \(x= \frac{5\pi}{6}   \);
 \(\quad\) one period starts at \(0\) and ends at \(   \frac{5\pi}{3}  \).

41. amplitude: \(  1  \); period: \(   \frac{12\pi}{5}  \) midline: \(y=  1  \);
 \(\quad\) maximum: \(y=  2  \) occurs at \(x=0\);
 \(\quad\) minimum: \(y=  0   \) occurs at \(x=  \frac{6\pi}{5}  \);
 \(\quad\) one period starts at \(0\) and ends at \(   \frac{12\pi}{5}  \).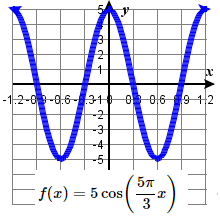

       

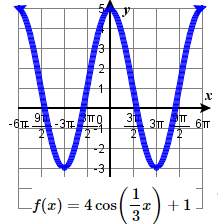43. amplitude: \(  4  \); period: \(   6 \pi  \) midline: \(y=  1  \);
 \(\quad\) maximum: \(y= 5   \) occurs at \(x=0\);
 \(\quad\) minimum: \(y=  -3   \) occurs at \(x=  3 \pi \);
 \(\quad\) one period starts at \(0\) and ends at \(  6 \pi  \).

45. amplitude: \(  5  \); period: \(   \frac{6}{5}  \) midline: \(y=  0  \);
 \(\quad\) maximum: \(y= 5   \) occurs at \(x=0\);
 \(\quad\) minimum: \(y=  -5   \) occurs at \(x=  \frac{3}{5}  \);
 \(\quad\) one period starts at \(0\) and ends at \(   \frac{6}{5}  \).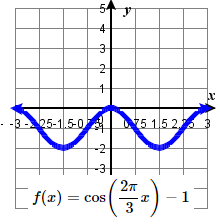

      

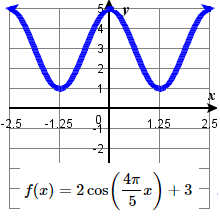47. amplitude: \(  2  \); period: \(   \frac{5}{2}  \) midline: \(y=   3 \);
 \(\quad\) maximum: \(y= 5   \) occurs at \(x=0\);
 \(\quad\) minimum: \(y=  1   \) occurs at \(x=  \frac{5}{4}  \);
 \(\quad\) one period starts at \(0\) and ends at \(   \frac{5}{2}  \).

49. amplitude: \(  1  \); period: \(  3   \) midline: \(y= -1   \);
 \(\quad\) maximum: \(y=  0  \) occurs at \(x=0\);
 \(\quad\) minimum: \(y=   -2  \) occurs at \(x=  \frac{3}{2}  \);
 \(\quad\) one period starts at \(0\) and ends at \(  3   \).

 

\( \star \)

C: Find attributes of sinusoidal functions

Exercise \(\PageIndex{C}\)

\( \bigstar \) For each of the following equations, find the amplitude, period, horizontal shift, and midline.

51. \(y=3\sin (8(x+4))+5 \\[2pt] \) 52. \(y=4\sin \left(\dfrac{\pi }{2} (x-3)\right)+7\)

53. \(y=2\sin (3x-21)+4 \\[2pt] \) 54. \(y=5\sin (5x+20)-2\)

55. \(y=\sin \left(\dfrac{\pi }{6} x+\pi \right)-3 \\[2pt] \) 56. \(y=8\sin \left(\dfrac{7\pi }{6} x+\dfrac{7\pi }{2} \right)+6\)

Answer

       51. Amp: 3, Period = \(\dfrac{\pi}{4}\), Shift: 4 left, Midline: \(y = 5\)
       53. Amp: 2, Period = \(\dfrac{2\pi}{3}\), Shift: 7 right, Midline: \(y = 4\)
       55. Amp: 1, Period = 12, Shift: 6 left, Midline: \(y = -3\)

D: Identify Attributes and Graph Phase-Shifted Sinusoidal Functions

Exercise \(\PageIndex{D}\)

\( \bigstar \) For the following exercises, state (a) the amplitude, vertical translation and midline, (b) the period, (c) the phase shift, and  (d) the maximum and minimum \(y\)-values and their corresponding \(x\)-values on one period. Give exact answers (fractions and multiples of pi, rather than decimal approximations). (e) Graph two full periods of each function.

61)  \( y= 3 \sin \left( \dfrac{\pi}{4} x  + \dfrac{\pi}{8}   \right) + 2 \\[2pt] \)  62)  \( y= 2 \sin  \left( \dfrac{\pi}{3}  x + \dfrac{\pi}{6} \right) -2   \\[2pt] \)   63)  \( y= -2 \sin \left( \dfrac{\pi}{2}  x  + \dfrac{\pi}{4} \right) +1    \\[2pt] \)   64)  \( y= -3 \sin  \left(\pi x  + \dfrac{\pi}{4} \right) + 1  \\[2pt] \)

65)  \( y= 4 \sin  \left( \pi x -  \dfrac{\pi}{3}  \right) -1  \\[2pt] \) 66)  \( y= 2 \sin \left( \dfrac{2\pi}{3 }   x - \dfrac{\pi}{3} \right) -3  \\[2pt]   \)   67)  \( y= 3 \sin \left( \dfrac{5}{3 }   x - \dfrac{\pi}{6} \right) - 2  \\[2pt] \)   68)  \( y=  \sin \left( \dfrac{1}{6}  x - \dfrac{\pi}{6} \right)  -  2 \\[2pt] \)

69)  \( y= 2 \sin \left(- \dfrac{4}{3 }   x + \dfrac{\pi}{3} \right) + 1 \\[2pt]  \) 70)  \( y= 4 \sin \left( -\dfrac{5}{3 }   x - \dfrac{\pi}{3}  \right)  -  1 \\[2pt] \) 71)  \( y= 4 \sin \left( \dfrac{5}{4} x - \dfrac{\pi}{2} \right) +1 \\[2pt]   \)

Answers to Odd Problems

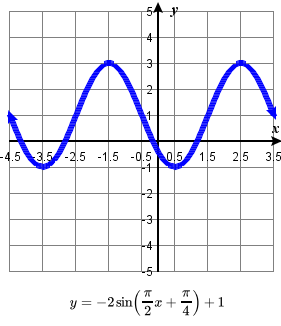
61. amplitude: \(   3  \); period: \(   8  \); midline: \(y= 2    \);
\( \quad \) vertical translation: up \(2\); horizontal shift: left \( \frac{1}{2}     \);
\( \quad \) one period occurs from \(x= -\frac{1}{2}  \) to \(x= \frac{15}{2}   \)
\( \quad \) maximum: \(y=5\) occurs at \(x =  \frac{3}{2} \);
\( \quad \) minimum: \(y=  -1   \) occurs at \(x = \frac{11}{2} \);

63. amplitude: \(2\); period: \(4\); midline: \(y=1\);
\( \quad \) vertical translation:  up \(1\); horizontal shift: left \( \frac{1}{2} \);
\( \quad \) one period occurs from \(x= -\frac{1}{2} \) to \(x= \frac{7}{2} \)
\( \quad \) maximum: \(y=3\) occurs at \(x = \frac{5}{2}  \);
\( \quad \) minimum: \(y=-1\) occurs at \(x = \frac{1}{2} \);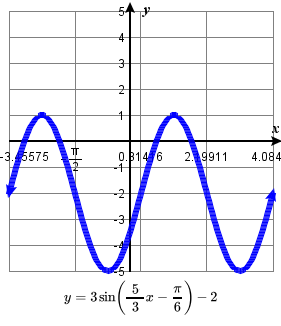

 

65. amplitude: \(4\); period: \(2 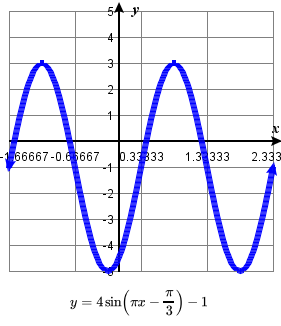\); midline: \(y=-1\);
\( \quad \) vertical translation: down \(1\);  horizontal shift:  right \( \frac{1}{3} \);
\( \quad \) one period occurs from \(x= \frac{1}{3} \) to \(x= \frac{7}{3} \)
\( \quad \) maximum: \(y=3\) occurs at \(x =  \frac{5}{6} \);
\( \quad \) minimum: \(y=-5\) occurs at \(x = \frac{11}{6} \);

67. amplitude: \(3\); period: \( \frac{6\pi}{5} \); midline: \(y=-2\);
\( \quad \) vertical translation: down \(2\);  horizontal shift: right \( \frac{\pi}{10} \);
\( \quad \) one period occurs from \(x= \frac{\pi}{10} \) to \(x= \frac{13\pi}{10} \)
\( \quad \) maximum: \(y=1\) occurs at \(x = \frac{2\pi}{5} \);
\( \quad \) minimum: \(y=-5\) occurs at \(x =  \pi\);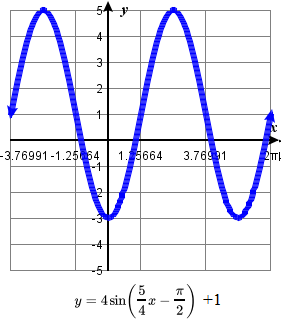

 

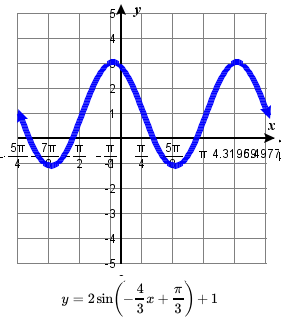69. amplitude: \(2\); period: \( \frac{3\pi}{2} \); midline: \(y=1\);
\( \quad \) vertical translation: up \(1\);  horizontal shift: right \( \frac{\pi}{4} \);
\( \quad \) one period occurs from \(x= \frac{\pi}{4} \) to \(x= \frac{7\pi}{4} \)
\( \quad \) maximum: \(y=3\) occurs at \(x = \frac{11\pi}{8} \);
\( \quad \) minimum: \(y=-1\) occurs at \(x = \frac{5\pi}{8} \);

71. amplitude: \(4\); period: \( \frac{8\pi}{5} \); midline: \(y=1\);
\( \quad \) vertical translation: none;  horizontal shift: right \( \frac{2\pi}{5} \);
\( \quad \) one period occurs from \(x= \frac{2\pi}{5} \) to \(x= 2\pi \)
\( \quad \) maximum: \(y=5\) occurs at \(x = \frac{4\pi}{5} \);
\( \quad \) minimum: \(y=-3\) occurs at \(x = \frac{8\pi}{5} \);

\( \bigstar \) For the following exercises, state (a) the amplitude, vertical translation and midline, (b) the period, (c) the phase shift, and  (d) the maximum and minimum \(y\)-values and their corresponding \(x\)-values on one period. Give exact answers (fractions and multiples of pi, rather than decimal approximations). (e) Graph two full periods of each function.

75)  \( y= \cos \left( \dfrac{\pi}{4} x -  \dfrac{\pi}{4} \right) + 3  \\[2pt]  \)  76)  \( y=  \cos \left( \dfrac{\pi}{6}  x -\dfrac{\pi}{3} \right)  -1 \\[2pt] \)   77)  \( y=  - \cos \left(  \dfrac{5\pi}{2} x -  \dfrac{\pi}{4} \right) + 2  \\[2pt]  \)    78)  \( y= - 3 \cos \left( \dfrac{5\pi}{6} x - \dfrac{\pi}{6} \right) - 1  \\[2pt] \)

79)  \( y= 4 \cos \left( \dfrac{3\pi}{2}  x + \dfrac{\pi}{4}\right) + 1  \\[2pt] \)   80)  \( y= 2  \cos \left( \dfrac{\pi}{2}  x + \dfrac{\pi}{3} \right) + 3  \\[2pt] \)  81)  \( y= 2 \cos \left( \dfrac{1}{3}  x + \dfrac{\pi}{3}  \right) -1  \\[2pt]  \) 82)  \( y= 2 \cos  \left( \dfrac{1}{2}  x + \dfrac{\pi}{6} \right) +2 \\[2pt]  \)

83)    97)  \( y=  \cos  \left(- 2 x  + \dfrac{\pi}{4}  \right) - 3 \\[2pt] \) 84)  \( y= 3 \cos \left(- \dfrac{5}{6} x - \dfrac{\pi}{3} \right)    \\[2pt]   \) 85)  \( y=  \cos \left( \dfrac{2}{3 }   x - \dfrac{\pi}{6}  \right)  + 4  \\[2pt]  \)

Answers to odd-numbered problems:

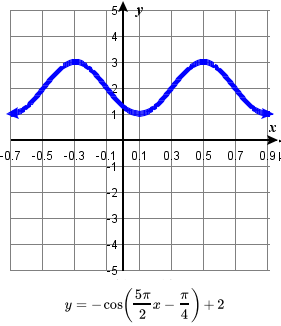
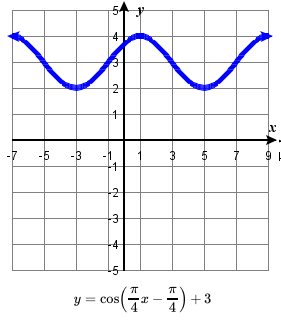75. amplitude: \(1\); period: \( 8 \); midline: \(y=3\);
\( \quad \) vertical translation: up \(3\);  horizontal shift: right \( 1 \);
\( \quad \) one period occurs from \(x= 1 \) to \(x= 9 \)
\( \quad \) maximum: \(y=4\) occurs at \(x = 1 \);
\( \quad \) minimum: \(y=2\) occurs at \(x = 5 \);

77. amplitude: \(1\); period: \( \frac{4}{5} \); midline: \(y=2\);
\( \quad \) vertical translation: up \(2\);  horizontal shift: right \( \frac{1}{10} \);
\( \quad \) one period occurs from \(x=  \frac{1}{10} \) to \(x=  \frac{9}{10} \)
\( \quad \) maximum: \(y=3\) occurs at \(x =  \frac{1}{2} \);
\( \quad \) minimum: \(y=1\) occurs at \(x =  \frac{1}{10} \);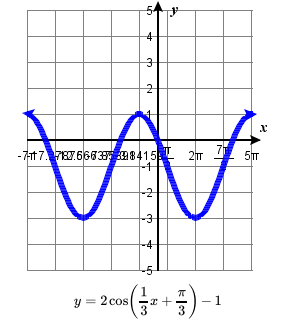

 

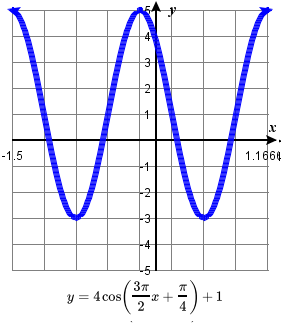79. amplitude: \(4\); period: \( \frac{4}{3} \); midline: \(y=1\);
\( \quad \) vertical translation: up \(1\);  horizontal shift: left \( \frac{1}{6} \);
\( \quad \) one period occurs from \(x=- \frac{1}{6} \) to \(x= \frac{7}{6} \)
\( \quad \) maximum: \(y=5\) occurs at \(x = -\frac{1}{6} \);
\( \quad \) minimum: \(y=-3\) occurs at \(x = \frac{1}{2} \);

81. amplitude: \(2\); period: \( 6\pi \); midline: \(y=-1\);
\( \quad \) vertical translation: down 1 \(\);  horizontal shift: left \( \pi \);
\( \quad \) one period occurs from \(x= -\pi \) to \(x= 5\pi \)
\( \quad \) maximum: \(y=1\) occurs at \(x = -\pi \);
\( \quad \) minimum: \(y=-3\) occurs at \(x = 2\pi \);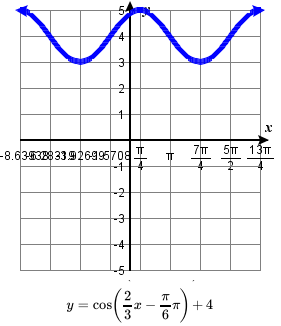

 

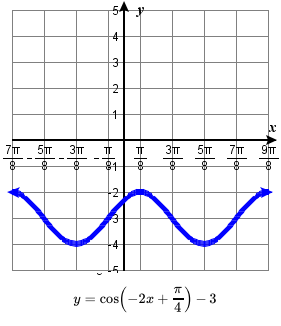83. amplitude: \(1\); period: \( \pi \); midline: \(y=-3\);
\( \quad \) vertical translation: down \(3\);  horizontal shift: right \( \frac{\pi}{8} \);
\( \quad \) one period occurs from \(x=  \frac{\pi}{8} \) to \(x=  \frac{9\pi}{8} \)
\( \quad \) maximum: \(y=-2\) occurs at \(x =  \frac{\pi}{8} \);
\( \quad \) minimum: \(y=-4\) occurs at \(x =  \frac{5\pi}{8} \);

85. amplitude: \(1\); period: \( 3\pi \); midline: \(y=4\);
\( \quad \) vertical translation: up \(4\);  horizontal shift: right \( \frac{\pi}{4} \);
\( \quad \) one period occurs from \(x= \frac{\pi}{4} \) to \(x= \frac{13\pi}{4} \)
\( \quad \) maximum: \(y=5\) occurs at \(x = \frac{\pi}{4} \);
\( \quad \) minimum: \(y=3\) occurs at \(x = \frac{7\pi}{4} \);

 

\( \bigstar \) For the following exercises, state (a) the amplitude, vertical translation and midline, (b) the period, (c) the phase shift, and  (d) the maximum and minimum \(y\)-values and their corresponding \(x\)-values on one period. Give exact answers (fractions and multiples of pi, rather than decimal approximations). (e) Graph two full periods of each function.

90. \(f(t)=2\sin \left(t-\dfrac{5\pi}{6} \right)\) 91. \(f(t)=-\sin \left (\dfrac{1}{2}t+\dfrac{5\pi}{3} \right ) \\[2pt] \) 92. \(f(x)=4\sin \left (\dfrac{\pi}{2}(x-3) \right )+7 \\[2pt] \)

95. \(f(t)=-\cos \left(t+\dfrac{\pi}{3} \right)+1 \\[2pt] \) 96. \(f(t)=4\cos \left(2\left (t+\dfrac{\pi}{4} \right ) \right)-3\)

97. \(y=3 \sin(8(x+4))+5 \\[2pt] \) 98. \(y=2 \sin(3x-21)+4 \\[2pt] \) 99. \(y=5 \sin(5x+20)-2 \\[2pt] \)

Answers to odd-numbered problems:

91. amplitude: \(1\); period: \(4\pi\); midline: \(y=0\); maximum: \(y=1\) occurs at \(t=\frac{11\pi}{3} \approx 11.52\); minimum: \(y=-1\) occurs at \(t=\frac{5\pi}{3} \approx 5.24\); phase shift: \(-\dfrac{10\pi}{3}\); vertical shift: \(0\); one full period is from \(t=\frac{2\pi}{3} \approx 2.094\) to \(t=\frac{14\pi}{3} \approx 14.661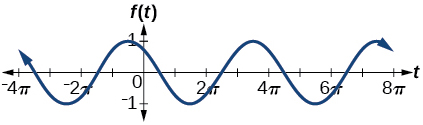 \)	95. amplitude: \(1\); period: \(2\pi \); midline: \(y=1\); maximum: \(y=2\) occurs at \(t=\frac{2\pi}{3} \approx 2.094\); minimum: \(y=0\) occurs at \(t=\frac{5\pi}{3} \approx 5.24\); phase shift: \(-\dfrac{\pi}{3}\); vertical translation: \(1\); one full period is from \(t=\frac{2\pi}{3} \approx 2.094\) to \(t=\frac{8\pi}{3} \approx 8.378 \)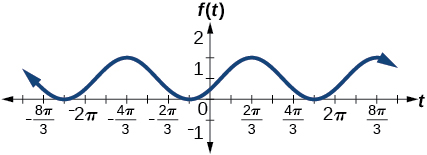
97. amplitude: \(3\); period: \(\dfrac{\pi}{4}\); midline: \(y=5\); maximum: \(y=8\) occurs at \(x = -4+\frac{21\pi}{16} \approx 0.123\); minimum: \(y=2\) occurs at \(x = -4+\frac{23\pi}{16} \approx 0.516\); horizontal shift: \(-4\); vertical translation \(5\); one period occurs from \(x=-4+\frac{22\pi}{16} \approx 0.320\)  to \(x=-4+\frac{26\pi}{16} \approx 1.105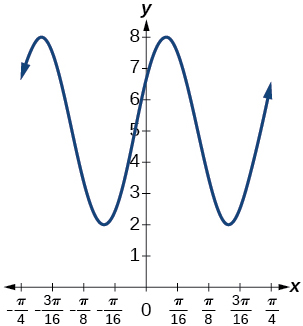  \)	99. amplitude: \(5\); period:\(\dfrac{2\pi }{5}\); midline: \(y=-2\); maximum: \(y=3\) occurs at \(x= -4+\frac{13\pi}{10} \approx 0.084\); minimum: \(y=-7\) occurs at \(x=-4+\frac{15\pi}{10} \approx 0.712\); phase shift: \(-4\); vertical translation: \(-2\); one full period can be graphed on \(x=-4+\frac{7\pi}{5} \approx 0.398\)  to \(x=-4+\frac{9\pi}{5} \approx 1.655 \)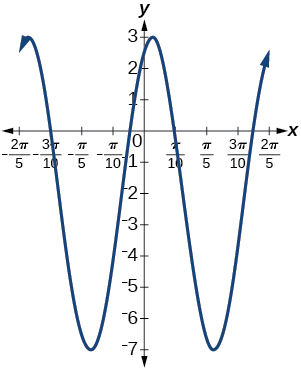

E: Construct an equation for a non-phase-shifted sinusoidal graph 

Exercise \(\PageIndex{E}\)

\(\bigstar\) For each non-phase shifted sine or cosine graph,  determine the amplitude, midline, and period, then find a formula for the function.

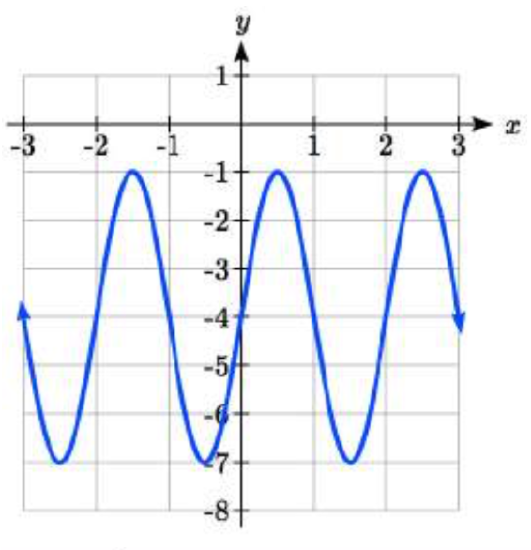
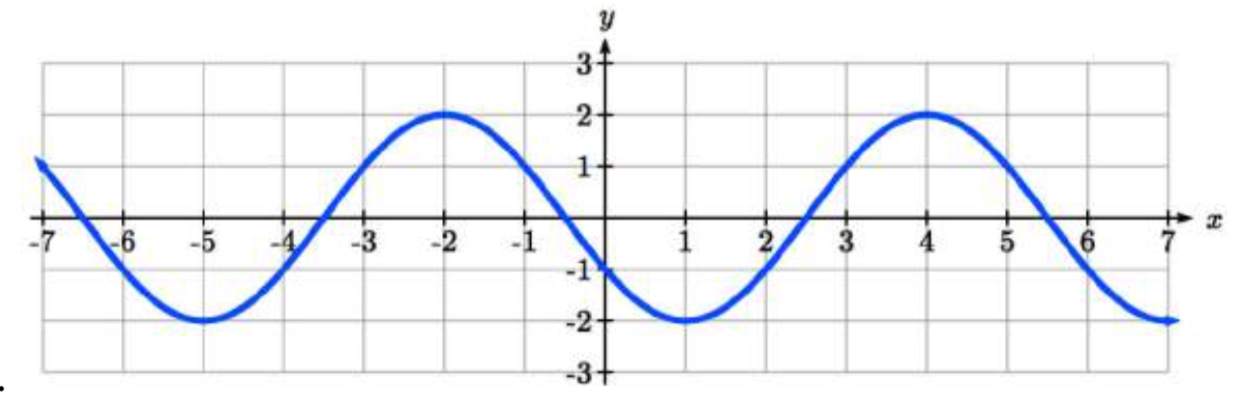
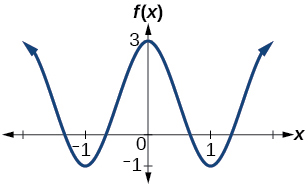
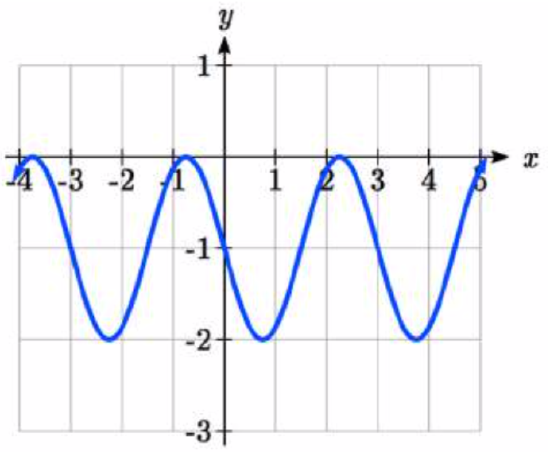
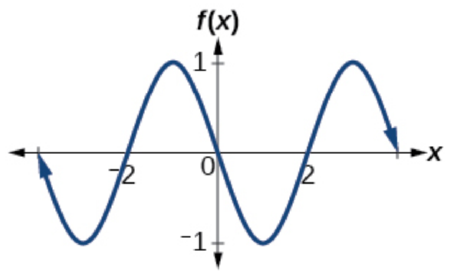
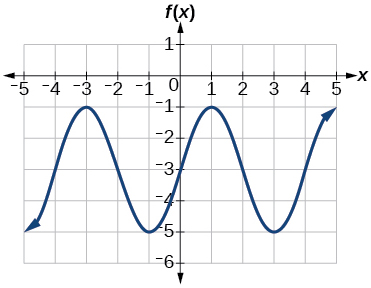
101. Figure \(\PageIndex{101}\)	102. Figure \(\PageIndex{102}\)	103. Figure \(\PageIndex{103}\)
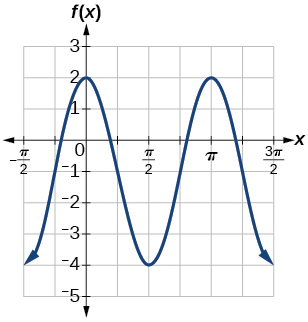
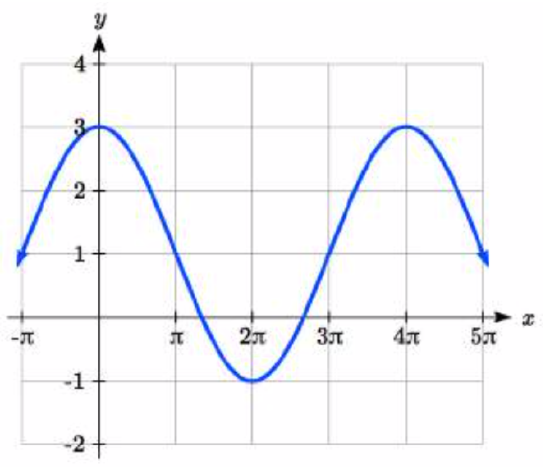
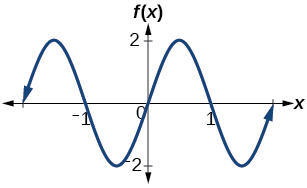
104. Figure \(\PageIndex{104}\)	105. Figure \(\PageIndex{105}\)	106.  Figure \(\PageIndex{106}\)
107.	108.	109.

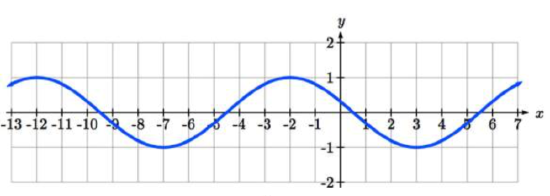
Answers to odd-numbered problems:

101. amplitude: \(2\); period: \(2\); midline \(y=1\) equation: \(f(x)=2\cos \left (\pi x \right )+1\)

103. amplitude: \(2\); midline: \(y=-3\) period: \(4\); equation: \(f(x)=2\sin \left (\dfrac{\pi}{2}x \right )-3\)
105. amplitude: \(2\); period: \(5\); midline: \(y=3\) equation: \(f(x)=-2\cos \left (\dfrac{2\pi}{5}x \right )+3\)

107. Amp: 3. Period = 2. Midline: \(y = -4\). \(f(t) = 3\sin(\pi t) - 4\)
109. Amp: 2. Period = \(4\pi\). Midline: \(y = 1\). \(f(t) = 2\cos(\dfrac{1}{2} t) + 1\)

F: Construct an equation for a phase-shifted sinusoidal graph 

Exercise \(\PageIndex{F}\)

\(\bigstar\) Find a formula for each of the functions graphed below.

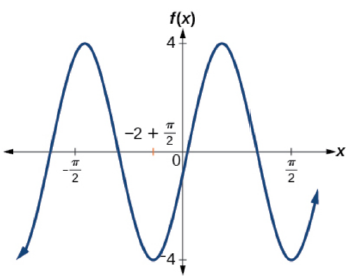
111.	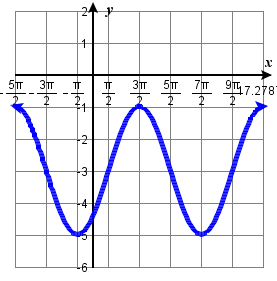112.
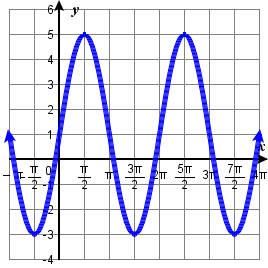113.	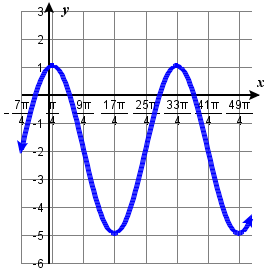114.
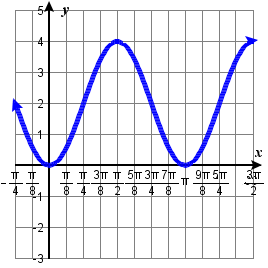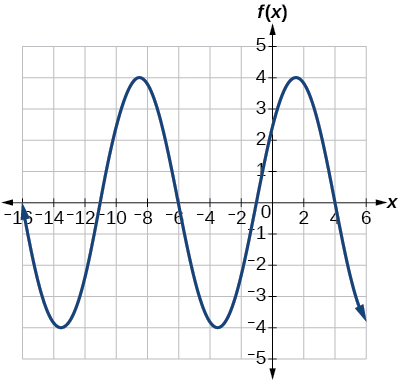
115.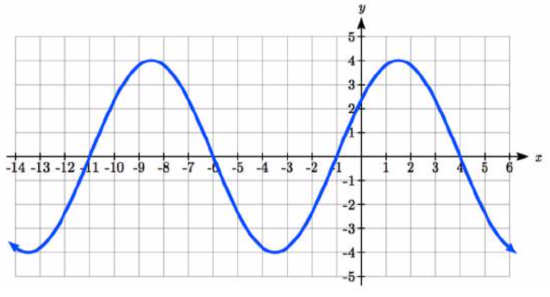	116.
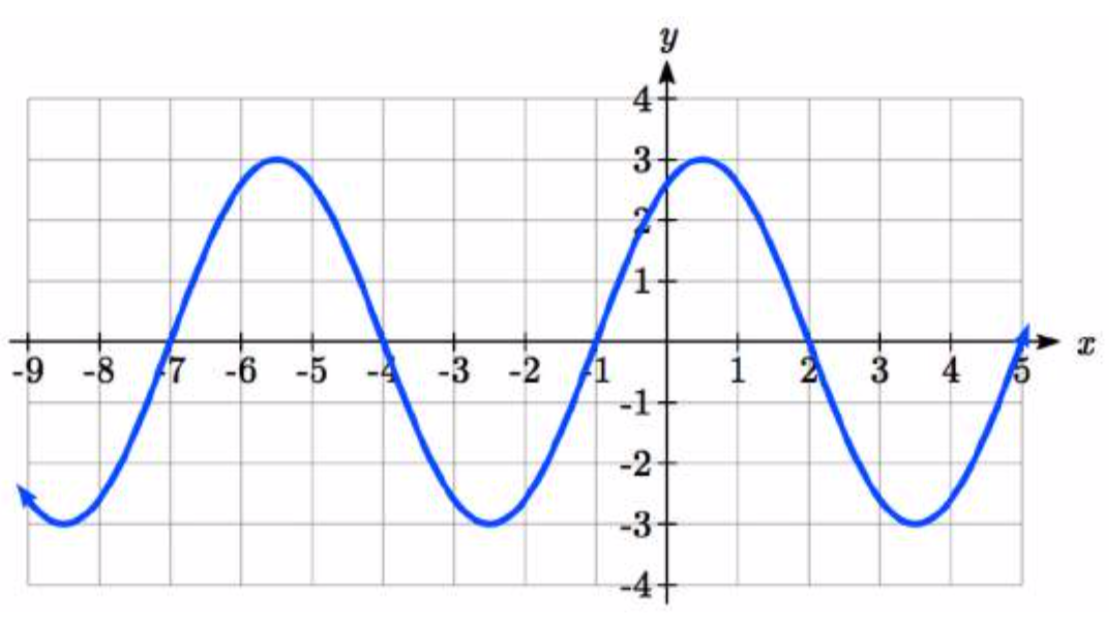117.	118.
119.	120.

Answers to odd-numbered problems:

111. \(f(x) = 2\sin(\frac{1}{2} x + \frac{\pi}{4})) - 3\)         113. \(f(x) = 3\cos(\frac{1}{4} x - \frac{\pi}{16})) - 2\)
115. \(f(x) = 4\sin(\dfrac{\pi}{5} (x + 1))\)         117. \(f(x) = \cos(\dfrac{\pi}{5} (x + 2))\)
119. amplitude: \(4\); period: \(2\); midline: \(y=0\) ;   equation: \(f(x)=-4\cos \left (\pi \left (x-\dfrac{\pi}{2} \right ) \right )\)

G: Find an equation for an application using a phase-shifted sinusoidal graph

Exercise \(\PageIndex{G}\) 

Note: In addition to constructing a sinusoidal equation, some of these problems also have an additional part that requires solving an equation. Solving sinusoidal equations is covered later in the next chapter.

Temperature

121. Outside temperatures over the course of a day can be modeled as a sinusoidal function. Suppose the high temperature of \(84°F\) occurs at 6PM and the average temperature for the day is \(70°F.\) (a) Construct an equation that models the daily temperature. (b) Find the temperature, to the nearest degree, at 7AM.

122. Outside temperatures over the course of a day can be modeled as a sinusoidal function. Suppose the high temperature of \(105°F\) occurs at 5PM and the average temperature for the day is \(85°F\). (a) Construct an equation that models the daily temperature. (b) Find the temperature, to the nearest degree, at 9AM.

123. Outside temperatures over the course of a day can be modeled as a sinusoidal function. Suppose the temperature varies between \(64°F\) and \(86°F\) during the day and the average daily temperature first occurs at 12 AM. (a) Construct an equation that models the daily temperature. (b) How many hours after midnight does the temperature first reach \(70°F\)?

124. Outside temperatures over the course of a day can be modeled as a sinusoidal function. Suppose the temperature varies between \(47°F\) and \(63°F\) during the day and the average daily temperature first occurs at 10 AM. (a) Construct an equation that models the daily temperature. (b) How many hours after midnight does the temperature first reach \(51°F\)?

125. Outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the temperature is 50 degrees at midnight and the high and low temperature during the day are 57 and 43 degrees, respectively. Assuming t is the number of hours since midnight, find a function for the temperature, D, in terms of t.

126. Outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the temperature is 68 degrees at midnight and the high and low temperature during the day are 80 and 56 degrees, respectively. Assuming t is the number of hours since midnight, find a function for the temperature, D, in terms of t.

Ferris Wheel

127. A Ferris wheel is \(45\) meters in diameter and boarded from a platform that is \(1\) meter above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes \(1\) full revolution in \(10\) minutes. (a) Construct an equation that models the height above ground \(t\) minutes after the wheel begins to turn. (b) How many minutes of the ride are spent higher than \(27\) meters above the ground? Round to the nearest second.

128. A Ferris wheel is \(20\) meters in diameter and boarded from a platform that is \(2\) meters above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes \(1\) full revolution in \(6\) minutes. (a) Construct an equation that models the height above ground \(t\) minutes after the wheel begins to turn. (b) How much of the ride, in minutes and seconds, is spent higher than \(13\) meters above the ground?

129. A Ferris wheel is 25 meters in diameter and boarded from a platform that is 1 meters above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 10 minutes. The function \(h(t)\) gives your height in meters above the ground t minutes after the wheel begins to turn.

a. Find the amplitude, midline, and period of \(h\left(t\right)\).
b. Find a formula for the height function \(h\left(t\right)\).
c. How high are you off the ground after 5 minutes?

130. A Ferris wheel is 35 meters in diameter and boarded from a platform that is 3 meters above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 8 minutes. The function \(h(t)\) gives your height in meters above the ground t minutes after the wheel begins to turn.

a. Find the amplitude, midline, and period of \(h\left(t\right)\).
b. Find a formula for the height function \(h\left(t\right)\).
c. How high are you off the ground after 4 minutes?

Ice melt

131. The sea ice area around the South Pole fluctuates sinusoidally between about \(18\) million square kilometers in September to \(3\) million square kilometers in March. (a) Construct an equation that models the sea ice area. (b) When are there more than 15 million square kilometers of sea ice? Give your answer as a range of dates, to the nearest day.

132. The sea ice area around the North Pole fluctuates sinusoidally between about \(6\) million square kilometers on September 1 to \(14\) million square kilometers on March 1. (a) Construct an equation that models the sea ice area. (b) When are there less than 9 million square kilometers of sea ice? Give your answer as a range of dates, to the nearest day.

Rainfall

133. During a \(90\)-day monsoon season, daily rainfall can be modeled by sinusoidal functions. A low of \(4\) inches of rainfall was recorded on day \(30\), and overall the average daily rainfall was \(8\) inches. (a) Construct an equation that models the daily rainfall during a monsoon season. (b) During what period was daily rainfall less than \(5\) inches?

134. During a \(90\)-day monsoon season, daily rainfall can be modeled by sinusoidal functions. The rainfall fluctuates between a low of \(2\) inches on day \(10\) and \(12\) inches on day \(55\). (a) Construct an equation that models the daily rainfall during a monsoon season. (b) During what period is daily rainfall more than \(10\) inches?

135. In a certain region, monthly precipitation peaks at \(24\) inches in September and falls to a low of \(4\) inches in March. (a) Construct an equation that models the monthly precipitation. (b) Identify the periods when the region is under flood conditions (greater than \(22\) inches) and drought conditions (less than \(5\) inches). Give your answer to the nearest day.

136. In a certain region, monthly precipitation peaks at \(8\) inches on June 1 and falls to a low of \(1\) inch on December 1. (a) Construct an equation that models the monthly precipitation. (b) Identify the periods when the region is under flood conditions (greater than \(7\) inches) and drought conditions (less than \(2\) inches). Give your answer to the nearest day. 

More

137.  The hour hand of the large clock on the wall in Union Station measures 24 inches in length. At noon, the tip of the hour hand is 30 inches from the ceiling. At 3 PM, the tip is 54 inches from the ceiling, and at 6 PM, 78 inches. At 9 PM, it is again 54 inches from the ceiling, and at midnight, the tip of the hour hand returns to its original position 30 inches from the ceiling. Let \(y\) equal the distance from the tip of the hour hand to the ceiling \(x\) hours after noon. Find the equation that models the motion of the clock and sketch the graph.  

138.  The height of the tide in a small beach town is measured along a seawall. Water levels oscillate between 7 feet at low tide and 15 feet at high tide. On a particular day, low tide occurred at 6 AM and high tide occurred at noon. Approximately every 12 hours, the cycle repeats. Find an equation to model the water levels.   

139.  The daily temperature in the month of March in a certain city varies from a low of \(24°F\) at 6 AM to a high of \(40°F.\) (a) Let \(t=0\) correspond to noon. Find a sinusoidal function to model daily temperature and sketch the graph. (b) Approximate the time when the temperature reaches the freezing point \(32 °F.\)    

140.  Blood pressure of \(\frac{120}{80}\) is considered to be normal. The top number is the maximum or systolic reading, which measures the pressure in the arteries when the heart contracts. The bottom number is the minimum or diastolic reading, which measures the pressure in the arteries as the heart relaxes between beats, refilling with blood. Thus, normal blood pressure can be modeled by a periodic function with a maximum of 120 and a minimum of 80.  In a blood pressure function, frequency represents the number of heart beats per minute. Frequency is the reciprocal of period and is \(80\) beats per minute for a normal heart rate.  Write a function that models the average person’s blood pressure, where \(f(t)\) represents the blood pressure at time \(t\), measured in minutes.   

Answers to odd exercises.

121. (a) \( y = - 14 \sin ( \frac{2\pi}{24} t) +70 \)  (b)  \(56 °F\)      
123. (a) \( y = -11 \sin ( \frac{2\pi}{24} t) +75 \)  (b)  \(1.8024\) hours      
125. \(D(t) = 50 - 7 \sin(\dfrac{\pi}{12}t)\)

127. (a) \( y = 22.5 \sin ( \frac{2\pi}{10} t + \frac{3\pi}{2}) +23.5 \)  (b) \(4:30\)     
129. (a). Amp: 12.5. Midline: \(y = 13.5\). Period: 10   (b). \(h(t) = -12.5 \cos (\tfrac{\pi}{5}t) + 13.5\)  or  \(h(t)=12.5\sin\left ( \tfrac{\pi}{5}(t-2.5) \right )+13.5\);   (c). \(h(t) = 26\) meters

131. (a) \( y = -7.5 \sin ( \frac{2\pi}{12} t) +10.5 \)  (b)  From July 8 to October 23     
133. (a) \( y = -5 \cos ( \frac{2\pi}{12} t) +10.5 \)  (b)  From day \(19\) through day \(40\)     
135. (a) \( y = -10 \sin ( \frac{2\pi}{10} t) +14 \)  (b)  Floods: July 24 through October 7. Droughts: February 4 through March 27 

137.  \(y=−24 \cos (\dfrac{π}{6}x)+54\)     138.  \(y=4 \cos (\dfrac{π}{6} t) +11 \)   
139.  (a) \(y=8 \sin (\frac{2π}{24}t)+32 \)  (b) The temperature reaches freezing at noon and at midnight.     
140.   \(f(t)=20 \sin (160πt)+100\) 

Extension - cyclical behaviour with a linear or exponential growth rate

140.1 A rabbit population oscillates \(15\) above and below average during the year, reaching the lowest value in January. The average population starts at \(650\) rabbits and increases by \(110\) each year. Find a function that models the population, \(P\), in terms of months since January, \(t\).

Answer 140.1

\(P(t)=−15 \cos \left(\dfrac{π}{6}t \right)+650+\dfrac{55}{6}t\)

140.2 A deer population oscillates \(19\) above and below average during the year, reaching the lowest value in January. The average population starts at \(800\) deer and increases by \(160\) each year. Find a function that models the population, \(P\), in terms of months since January, \(t\).

140.3 A fish population oscillates \(40\) above and below average during the year, reaching the lowest value in January. The average population starts at \(800\) fish and increases by \(4\%\) each month. Find a function that models the population, \(P\), in terms of months since January, \(t\).

Answer 140.3

\(P(t)=−40 \cos \left(\dfrac{π}{6}t \right)+800(1.04)^t\)

140.4 A muskrat population oscillates \(33\) above and below average during the year, reaching the lowest value in January. The average population starts at \(900\) muskrats and increases by \(7\%\) each month. Find a function that models the population, \(P\), in terms of months since January, \(t\).

 

H: Unit Circle concepts 

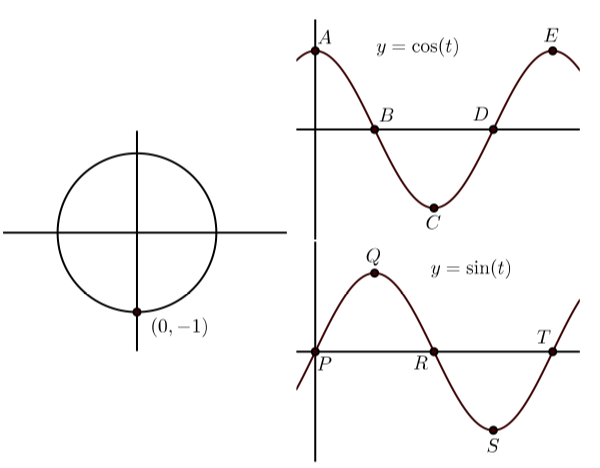
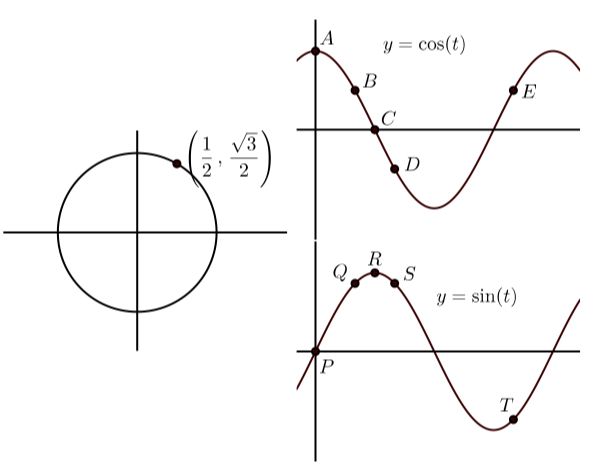
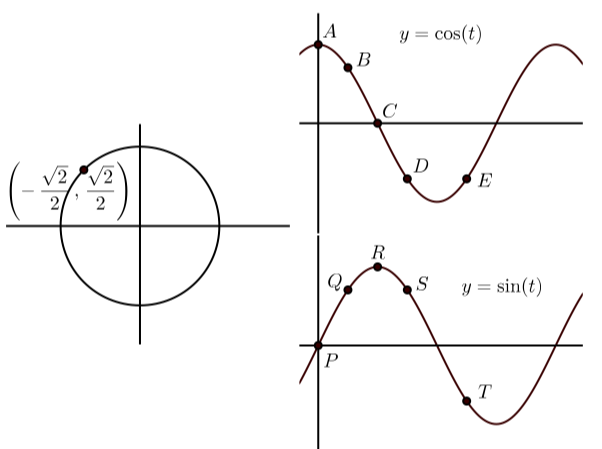
Exercise \(\PageIndex{H}\)

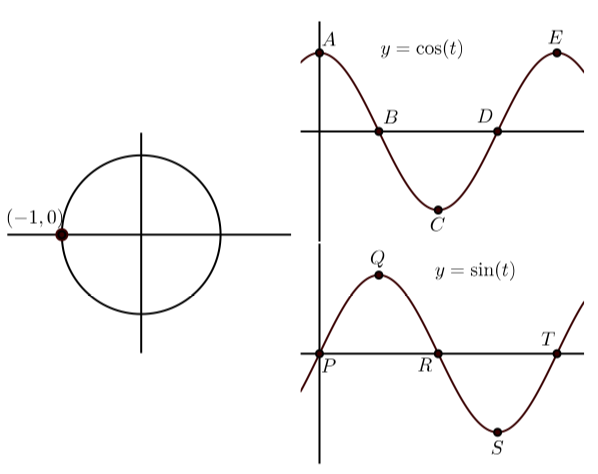
\( \bigstar \) In each of the following, the graph on the left shows the terminal point of an arc \(t\) (with \(0 \leq t \leq 2\pi\)) on the unit circle. The graphs on the right show the graphs of \(y = \cos(t)\) and \(y = \sin(t)\) with some points on the graph labeled. Match the point on the graphs of \(y = \cos(t)\) and \(y = \sin(t)\) that correspond to the point on the unit circle. In addition, state the coordinates of the points on \(y = \cos(t)\) and \(y = \sin(t)\).

141.	142.
143.	144.

Answers to odd exercises.

141. \(C(\pi, -1)\) \(R(\pi, 0)\)         143. \(B(\dfrac{\pi}{3}, \dfrac{1}{2})\) \(Q(\dfrac{\pi}{3}, \dfrac{\sqrt{3}}{2})\)