5.4: The Other Trigonometric Functions

In the previous section, we defined the sine and cosine functions as ratios of sides of a right triangle formed by the point of intersection \((x, y)\) between a circle of radius \(r\) and the terminal side of an angle in standard position. Since a triangle has 3 sides, there are 6 possible combinations of ratios. While the sine and cosine are the two prominent ratios that can be formed, there are four others, and together they define the 6 trigonometric functions.

Definition: Sine, Cosine, Tangent, Secant, Cosecant, and Cotangent Functions

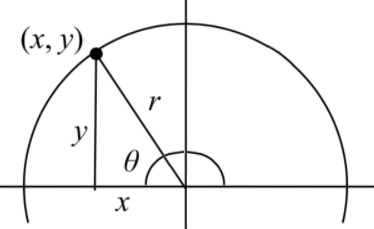For the point (\(x\), \(y\)) on a circle of radius \(r\) at an angle of \(\theta\), six trigonometric functions are defined as the ratios of the sides of the corresponding triangle. They are given below.

\(\qquad\) The sine function: \(\;\;\;\;\;\;\;\sin (\theta )=\dfrac{y}{r}\) \(\qquad\) The cosecant function: \(\;\;\;\csc (\theta )=\dfrac{r}{y}\)

\(\qquad\) The cosine function: \(\;\;\;\cos (\theta )=\dfrac{x}{r}\) \(\qquad \) The secant function: \(\;\;\;\;\;\;\sec (\theta )=\dfrac{r}{x}\)

\(\qquad\) The tangent function: \(\tan (\theta )=\dfrac{y}{x}\) \(\qquad\) The cotangent function: \(\cot (\theta )=\dfrac{x}{y}\)

The signs that \(x\) and \(y\) have depend on the quadrant the terminal side of the angle is in. The sign of \(r\) is always positive and \(r=\sqrt{x^2+y^2}\). Geometrically, notice that the definition of tangent corresponds with the slope of the line segment between the origin (0, 0) and the point (\(x\), \(y\)). This relationship can be very helpful in thinking about tangent values.

Use Definitions to Obtain Trigonometric Function Values 

If the coordinates of a point on the terminal side of an angle are known, the values of the trigonometric function can be found using the definitions.

Given a point on the terminal side of an angle.

Example \(\PageIndex{1a}\): Find trigonometric ratios given a point on the terminal side of an angle

The point (-1, 7) is on the terminal side of some angle \(\theta\). Evaluate the six trigonometric functions for this angle.

Solution

We know a triangle is formed in the 2nd Quadrant, with sides \(x=-1\) and \(y=7\).
The Pythagorean Theorem can be used to find the third side: \(r=\sqrt{x^2+y^2}=\sqrt{(-1)^2+7^2}=\sqrt{50} = 5\sqrt{2}\).

Now the definitions of the six trigonometric functions can be used to obtain the desired function values.

\(\sin\theta = \dfrac{y}{r} = \dfrac{7}{5\sqrt{2}} = \dfrac{7}{5\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{7\sqrt{2}}{10}\)	\(\cos\theta = \dfrac{x}{r} = \dfrac{-1}{5\sqrt{2}} = \dfrac{-1}{5\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}}=-\dfrac{\sqrt{2}}{10} \)	\(\tan\theta = \dfrac{y}{x} = \dfrac{7}{-1} = -7\)
\(\csc\theta = \dfrac{r}{y} = \dfrac{5\sqrt{2}}{7} \)	\(\sec\theta = \dfrac{r}{x} = \dfrac{5\sqrt{2}}{-1} = -5\sqrt{2} \)	\(\cot\theta = \dfrac{x}{y} =- \dfrac{1}{7} \)

Example \(\PageIndex{1b}\)

Figure \(\PageIndex{1b}\)

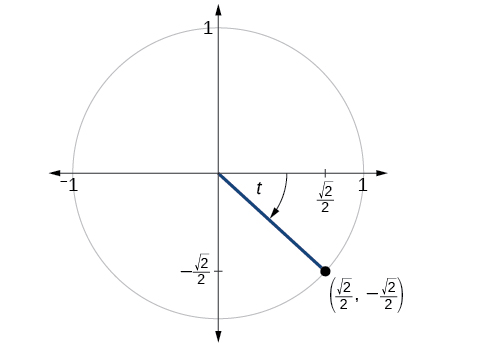
The point \(\left(\dfrac{\sqrt{2}}{2},−\dfrac{\sqrt{2}}{2}\right)\) is on the unit circle, as shown in Figure \(\PageIndex{1b}\). Find \( \sin t, \cos t, \tan t, \sec t, \csc t,\) and \( \cot t\).

Solution

Because this is a point on the unit circle, \(r=1\), and furthermore, \(x= \dfrac{\sqrt{2}}{2} \) and \(y= −\dfrac{\sqrt{2}}{2}\). Using these values for \(x\), \(y\), and \(r\) and the definitions, the values of the six trigonometric ratios are obtained. (Because this is a point on the unit circle, we could have directly stated the values of \(  \sin t = y\) and \( \cos t = x\), but the definitions were used below.) 

\( \sin t =\dfrac{y}{r}=\dfrac{-\frac{\sqrt{2}}{2}}{1} = −\dfrac{\sqrt{2}}{2}\)	\( \cos t = \dfrac{x}{r} =\dfrac{\frac{\sqrt{2}}{2}}{1} = \dfrac{\sqrt{2}}{2}\)	\( \tan t = \dfrac{y}{x} = \dfrac{-\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = -1\)
\( \csc t = \dfrac{r}{y} =\dfrac{1}{-\frac{\sqrt{2}}{2}} =-\dfrac {2}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}}=-\sqrt{2} \)	\( \sec t = \dfrac{r}{y} =\dfrac{1}{\frac{\sqrt{2}}{2}} =\sqrt{2} \)	\( \cot t = \dfrac{x}{y} = \dfrac{\frac{\sqrt{2}}{2}}{-\frac{\sqrt{2}}{2}} = -1\)

Try It \(\PageIndex{1}\)

Figure \(\PageIndex{1c}\)

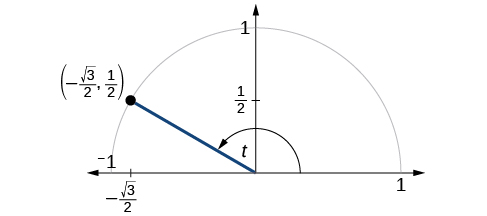
1. Suppose the terminal side of \(\theta\), when plotted in standard position, contains the point \(Q(3,-4)\). Evaluate the six trigonometric functions for this angle.
2. The point \(\left(−\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right)\) is on the unit circle, as shown in Figure \(\PageIndex{1c}\). Find \( \sin t, \cos t, \tan t, \sec t, \csc t,\) and \( \cot t\).

Answers

1. Since \(x = 3\) and \(y=-4\),
    then \(r = \sqrt{x^2 + y^2} = \sqrt{(3)^2+(-4)^2} = \sqrt{25} = 5\).

\(\sin(\theta) = -\dfrac{4}{5}\), \(\quad\) \(\cos(\theta) = \dfrac{3}{5}\), \(\quad\) \(\tan(\theta) = -\dfrac{4}{3}\), \(\quad\) \(\csc(\theta) = -\dfrac{5}{4}\), \(\quad\) \(\sec(\theta) = \dfrac{5}{3}\), \(\quad\) \(\cot(\theta) = - \dfrac{3}{4}\).

2. We have \(x= -\dfrac{\sqrt{3}}{2} \) and \(y=\dfrac{1}{2}\). Because this is a point on the unit circle, \(r=1\).

\(\sin(\theta) = \dfrac{1}{2}\), \( \; \) \(\cos(\theta) = -\dfrac{\sqrt{3}}{2}\), \( \; \) \(\tan(\theta) = -\dfrac{\sqrt{3}}{3}\), \( \; \) \(\csc(\theta) = 2\), \( \; \) \(\sec(\theta) = -\dfrac{2\sqrt{3}}{3}\), \( \;\) \(\cot(\theta) = - \sqrt{3}\).

Given one trigonometric ratio, find other trigonometric ratios

When given a trigonometric ratio, it is possible to narrow down the possible quadrants the angle is in to two, based on the definition of the trigonometric ratio and the signs that \(x\) and \(y\) take on in the different quadrants.

\( \sin \theta =\dfrac{y}{r}, \; \csc \theta = \dfrac{r}{y} \) \( \begin{array}{c|c} \text{QII: } + & \text{QI: }+ \\[2pt] \hline \text{ } & \text{ } \\[2pt] \end{array} \)	\( \cos \theta =\dfrac{x}{r}, \; \sec \theta = \dfrac{r}{x} \) \( \begin{array}{c|c} \qquad \text{ } & \text{QI: }+ \\[2pt] \hline \text{ } & \text{QIV: }+ \\[2pt] \end{array} \)	\( \tan \theta =\dfrac{y}{x}, \; \cot \theta = \dfrac{x}{y} \) \( \begin{array}{c|c} \text{ } & \text{QI: }+ \\[2pt] \hline \text{QIII: }+& \text{ } \\[2pt] \end{array} \)
Figure \(\PageIndex{2}\). Quadrants in which trigonometric functions are positive

If given a trigonometric ratio, the definitions can be used 'in reverse' to determine the values of two of the three legs (\(x\), \(y\), and \(r\) ) of a right triangle inscribed in the circle. Remember \(r\) is ALWAYS positive, so the sign of the ratio depends entirely on the signs of \(x\) and \(y\).

How to: Find trig ratios given one trig ratio.

Reference Triangle or Pythagorean Theorem Approach. Given a trigonometric ratio and perhaps some other information.

1. Determine the quadrant the angle is in, and the signs of \(x\) and \(y\) for any point on the terminal side of the angle.
2. Use the definition of the given trigonometric function and the quadrant it is in to determine two of the three sides of a reference triangle and their appropriate signs.
3. Use the Pythagorean Theorem to find the third side, and its appropriate sign. Now all three sides of the reference triangle are known.
4. Use the definitions to determine the other trigonometric ratios. 

Given a quadrant the angle is in

Example \(\PageIndex{2}\) Find Trigonometric Functions given one Trig Ratio and the quadrant the angle is in

Given \(\sec(\theta) = \dfrac{2\sqrt{6}}{3} \) with \(\theta\) in Quadrant IV. Find the value of \(\sin \theta\) and \(\cot \theta \).

Solution

Step 1. Angle \(\theta\) is in QIV where \(x > 0\) and \(y<0\).

Step 2. \(\sec (\theta )=\dfrac{2\sqrt{6}}{3}= \dfrac{r}{x}\), therefore we can choose \(r=2\sqrt{6}\) and \(x=3\)

Step 3. Find \(y\) with the Pythagorean Theorem: \(x^2+y^2=r^2 \Rightarrow 3^2+y^2 = (2\sqrt{6})^2 \Rightarrow y^2=4(6)-9=15.\) Since \(y\) is known to be negative, \(y=-\sqrt{15}\).

Step 4. Using the definitions,

\(\sin \theta = \dfrac{y}{r} = \dfrac{-\sqrt{15}}{2\sqrt{6}}=\dfrac{-\sqrt{15}}{2\sqrt{6}} \cdot \dfrac{\sqrt{6}}{\sqrt{6}} = \dfrac{-\sqrt{90}}{2(6)}= \dfrac{-3\sqrt{10}}{12}= -\dfrac{\sqrt{10}}{4} \) and

\(\cot \theta =\dfrac{x}{y}= \dfrac{3}{-\sqrt{15}} = \dfrac{3}{-\sqrt{15}} \cdot \dfrac{\sqrt{15}}{\sqrt{15}} = -\dfrac{3\sqrt{15}}{15} = -\dfrac{\sqrt{15}}{5}\)

Try It \(\PageIndex{2}\)

Suppose \(\theta\) is a Quadrant IV angle with \(\cot(\theta) = -4\). Find the values of the five remaining circular functions of \(\theta\).

Answers

We need to find a point \(Q(x,y)\) which lies on the terminal side of \(\theta\), when \(\theta\) is plotted in standard position. Since \(\theta\) is a Quadrant IV angle, we also know \(x>0\) and \(y< 0\).

We have that \(\cot(\theta) = -4 = \frac{x}{y} \). We may choose any values \(x\) and \(y\) so long as \(x>0\), \(y<0\) and \(\frac{x}{y} = -4\). (For example, we could choose \(x=8\) and \(y=-2\) or we could choose \(x = 4\) and \(y = -1\).

Using \(x = 4\) and \(y = -1\) we obtain \(r = \sqrt{x^2+y^2} = \sqrt{(4)^2 + (-1)^2} = \sqrt{17}\).

Thus \(\sin(\theta) =- \dfrac{1}{\sqrt{17}} = -\dfrac{\sqrt{17}}{17}\), \(\cos(\theta) = \dfrac{4}{\sqrt{17}} = \dfrac{4 \sqrt{17}}{17}\), \(\tan(\theta) = -\dfrac{1}{4}\), \(\sec(\theta) = \dfrac{\sqrt{17}}{4}\), \(\csc(\theta) = - \sqrt{17}\).

Given a range of angle values 

If a range of values an angle can have is given, that information can be translated to the quadrant the angle is in, and therefore the signs that \(x\) and \(y\) can take on. This follows from the definition of an angle in standard position.

\( \begin{array}{c|c}
\text{QII: } \dfrac{\pi}{2} < \theta < \pi & \text{QI: } \;\;\;\; 0 < \theta < \dfrac{\pi}{2} \\[2pt]
\qquad \quad 90^{\circ} < \theta < 180^{\circ} & \qquad \quad 0^{\circ} < \theta < 90^{\circ} \\[2pt]
\hline
\text{QIII: } \;\;\;\; \pi < \theta < \dfrac{3\pi}{2} & \text{QIV: } \dfrac{3\pi}{2} < \theta < 2 \pi \\[2pt]
\qquad \;\;\; 180^{\circ} < \theta < 270^{\circ} & \qquad \quad 270^{\circ} < \theta < 360^{\circ} \\[2pt]
\end{array} \)

Figure \(\PageIndex{3}\). Values of Angles in Standard Position in the Different Quadrants

Example \(\PageIndex{3}\): Use Definitions to Evaluate Trigonometric Functions

1. If \(\sin (\phi )=-\dfrac{3}{7}\) and \(\dfrac{3\pi }{2} <\phi < 2\pi\), find \(\cos (\phi )\) and \(\tan (\phi )\).
2. If \(\tan(\theta) = 3\) and \(\pi < \theta < \dfrac{3\pi}{2},\) find \(\sin\left(\theta\right)\).

Solution

1. \(\quad \; \)Angle \(\phi\) is in QIV where \(x > 0\) and \(y<0\).

\(\sin (\phi )=-\dfrac{3}{7} = \dfrac{y}{r}\), therefore we can choose \(r=7\) and \(y=-3\)

Find \(x\) with the Theorem of Pythagoras: \(x^2+y^2=r^2 \Rightarrow x^2+(-3)^2 = 7^2 \Rightarrow x^2=49-9=40\). Thus \(x=\pm\sqrt{40}\). Because \(x\) is known to be positive, \(x=2\sqrt{10}\).

Using the definitions, \(\cos (\phi )= \dfrac{x}{r} = \dfrac{2\sqrt{10}}{7}\) and \(\tan (\phi )\ = \dfrac{y}{x} = \dfrac{-3}{2\sqrt{10}} = \dfrac{3\sqrt{10}}{20} \).

2. \(\quad \; \)Angle \(\theta\) is in QIII where \(x < 0\) and \(y<0\).

\(\tan(\theta) = 3=\dfrac{3}{1} = \dfrac{y}{x},\) and because \(\theta\) is in QIII, \(x=-1\) and \(y=-3\)

Find \(r\) with the formula \(r=\sqrt{x^2+y^2} \Rightarrow r=\sqrt{(-1)^2+(-3)^2} \Rightarrow r=\sqrt{10}\).

Using the definitions, \(\sin (\theta)= \dfrac{y}{r} = -\dfrac{3}{\sqrt{10}} = -\dfrac{3\sqrt{10}}{10}. \)

Try It \(\PageIndex{3}\)

If \( \sec (t)=− \dfrac{17}{8}\) and \(0<t<π,\) find the values of the other five trigonometric functions.

Answers

\(t\) is in QII where \(x < 0\) and \(y>0\). \(x = -8\), \(y = 15\), and \(r = 17\).

\( \sin t=\dfrac{15}{17}, \quad \cos t=−\dfrac{8}{17}, \quad \tan t=−\dfrac{15}{8}, \quad \csc t= \dfrac{17}{15}, \quad \cot t=−\dfrac{8}{15} \).

Given the sign of another trigonometric ratio

Example \(\PageIndex{4}\); Find other trig ratios given one trig ratio and the sign of another ratio

1. If \(\csc(θ) = -\dfrac{10}{7}\) and \(\tan(θ) > 0\), determine the exact values of \(\cos(θ)\) and \(\tan(θ)\).
2. If \(\cot(t) =-6 \) and \(\cos(t) < 0\), determine the exact values of \(\sin(t)\) and \(\sec(t)\).

1. Solution

Step 1. Angle \(θ\) is either in QIII or QIV because \(\csc θ< 0\). Angle \(θ\) is in either QI or QIII because \(\tan θ> 0\).
Therefore \(θ\) must be in QIII where \(x < 0\) and \(y<0\).

Step 2. \(\csc(θ) = -\dfrac{10}{7} = \dfrac{r}{y}\), therefore we can choose \(r=10\) and \(y=-7\)

Step 3. Find \(x\) with the Theorem of Pythagoras: \(x^2+y^2=r^2 \Rightarrow x^2+(-7)^2 = 10^2\) \(\Rightarrow x^2=100-49=51.\) Thus \(x=\pm\sqrt{51}\). Because \(x\) is known to be negative, \(x=-\sqrt{51}\).

Step 4. Using the definitions, \(\cos(θ) = \dfrac{x}{r}=-\dfrac{\sqrt{51}}{10}\) and \(\tan(θ)=\dfrac{y}{x} = \dfrac{-7}{-\sqrt{51}} = \dfrac{7\sqrt{51}}{51}\)

 

2. Solution

Step 1. Angle \(t\) is either in QII or QIV because \(\cot t < 0\). Angle \(t\) is in either QII or QIII because \(\cos t > 0\).
Therefore \(t\) must be in QII where \(x < 0\) and \(y>0\).

Step 2. \(\cot(t) = -6 = -\dfrac{6}{1} = \dfrac{x}{y}\), and because \(t\) is in QII, \(x=-6\) and \(y=1\)

Step 3. Find \(r\) with the formula \(r=\sqrt{x^2+y^2} \Rightarrow r=\sqrt{(-6)^2+1^2} \Rightarrow r=\sqrt{37}\).

Step 4. Using the definitions, \(\sin(t)= \dfrac{y}{r} = \dfrac{1}{\sqrt{37}}= \dfrac{\sqrt{37}}{37}\) and \(\sec(t) = \dfrac{r}{x} = -\dfrac{\sqrt{37}}{6}\)

Try It \(\PageIndex{4}\)

If \(\sec(θ) = 3 \) and \(\sin(θ) < 0\), find the values of the other five trigonometric functions.

Answers

\(θ\) is in QIV where \(x > 0\) and \(y<0\). \(x = 1\), \(y = -2\sqrt{2}\), and \(r = 3\).

\(\sin(\theta) = -\dfrac{2\sqrt{2}}{3}\), \(\qquad\) \(\cos(\theta) = -\dfrac{1}{3}\), \(\qquad\) \(\tan(\theta) = -2\sqrt{2}\), \(\qquad\) \(\csc(\theta) = -\dfrac{3\sqrt{2}}{4}\), \(\qquad\) \(\cot(\theta) = - \dfrac{\sqrt{2}}{4}\).

Given only one trigonometric ratio

Notice in the problems above we were given both a trigonometric ratio and the quadrant the angle was in. When the quadrant is not given, there are two possible solutions, as the example below illustrates.

Example \(\PageIndex{5}\)

Given \(\cos θ = − \dfrac{4}{ 5}\), draw possible angles for \(\theta\) in standard position and determine the value of \(\sin \theta\) and \(\tan \theta\).

Solution

Figure \(\PageIndex{5}\): \( \cos \theta = - \dfrac{4}{5} \)

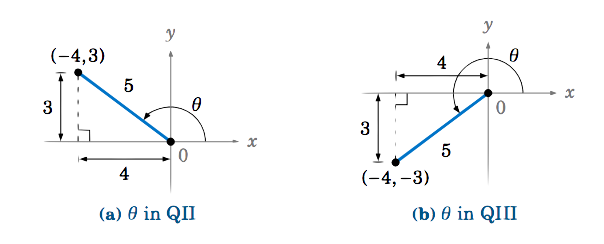
Given \(\cos θ = \dfrac{x}{r} =− \dfrac{4}{ 5}\) we can conclude a point on the terminal side of \(\theta\) has coordinate \((-4, y)\) on a circle of radius \(r=5\).

Using the Pythagorean Theorem to determine \(y\) we find \(x^2+y^2=r^2 \Rightarrow (-4)^2 + y^2 = 5^2 \Rightarrow y^2=9 \Rightarrow y = \pm 3\).

Thus there are actually two possible angles for \(\theta\).

If the point \((-4,3) \) is on the terminal side of \(\theta \), then \(\theta \) is in QII, and so we have \(x = -4 \), \(y = 3 \), and \(r = 5 \). Thus, \(  \boxed{ \sin\;\theta = \dfrac{y}{r} = \dfrac{3}{5} } \) and \(  \boxed{ \tan\;\theta = \dfrac{y}{x} = \dfrac{3}{-4} }. \)

If the point \((-4,-3) \) is on the terminal side of \(\theta \), then \(\theta \) is in QIII, and so we have \(x = -4 \), \(y = -3 \), and \(r = 5 \). Thus, \( \boxed{  \sin \theta = \dfrac{y}{r} = \dfrac{-3}{5}  } \) and \(   \boxed{  \tan \theta = \dfrac{y}{x} = \dfrac{-3}{-4} = \dfrac{3}{4} }. \)

Trigonometric Function Values From Identities

Whenever a trigonometric ratio is given, and other function values are desired, there are two different approaches that can be used. We have been illustrating the use of the definitions and the Pythagorean Theorem. Another approach which will now be discussed uses identities.

Reciprocal and Quotient Identities

You may have noticed that the ratios defining the secant, cosecant, and cotangent are the reciprocals of the ratios defining the cosine, sine, and tangent functions, respectively. Additionally, notice that

\(\tan (\theta )=\dfrac{y}{x} =\dfrac{r\sin (\theta )}{r\cos (\theta )} =\dfrac{\sin (\theta )}{\cos (\theta )}\)

Applying this concept to the other trigonometric functions we can state the Reciprocal and Quotient Identities.

Identities

Reciprocal Identities	\(\csc (\theta )=\dfrac{1}{\sin (\theta )}\)	\(\sec (\theta )=\dfrac{1}{\cos (\theta )}\)	\(\cot (\theta )=\dfrac{1}{\tan (\theta )}\)
	\(\sin (\theta )=\dfrac{1}{\csc (\theta )}\)	\(\cos (\theta )=\dfrac{1}{\sec (\theta )}\)	\(\tan (\theta )=\dfrac{1}{\cot (\theta )}\)
Quotient Identities	\(\tan (\theta )=\dfrac{\sin (\theta )}{\cos (\theta )}\)	\(\cot (\theta )=\dfrac{\cos (\theta )}{\sin (\theta )}\)

These relationships are called identities. Identities are statements that are true for all values of the input on which they are defined. Identities are usually something that can be derived from definitions and relationships we already know.

Trigonometric Functions of Special Angles

Example \(\PageIndex{6a}\): Using Identities to Evaluate Trigonometric Functions

1. Given \( \sin (45°)= \dfrac{\sqrt{2}}{2} \) and \( \cos (45°)= \dfrac{\sqrt{2}}{2}\), use identities to evaluate \( \tan(45°).\)
2. Given \( \sin \left(\dfrac{5π}{6}\right)= \dfrac{1}{2} \) and \(  \cos \left(\dfrac{5π}{6}\right)=−\dfrac{\sqrt{3}}{2},\) use identities to evaluate \(\sec \left(\dfrac{5π}{6}\right) \).

Solution

Because we know the sine and cosine values for these angles, we can use identities to evaluate the other functions.

\( \text{a.} \quad \text{Use the quotient identity for tangent.} \quad \text{tan} (45^{\circ}) = \dfrac{\text{sin} (45^{\circ})}{\text{cos} (45^{\circ})} = \dfrac{\sqrt{2}/2}{\sqrt{2}/2} = 1\)

Notice this result is consistent with our interpretation of the tangent value as the slope of the line passing through the origin at the given angle: a line at 45 degrees would indeed have a slope of 1.

\( \text{b.} \quad \text{Use the reciprocal identity for secant.} \quad \text{sec}\left(\dfrac{5\pi}{6}\right) = \dfrac{1}{\cos\left(\tfrac{5\pi}{6}\right)} = \dfrac{1}{-\frac{\sqrt{3}}{2}} = \dfrac{-2}{\sqrt{3}}= \dfrac{-2\sqrt{3}}{3}\)

We know the values of sine and cosine for "special" angles \(0\), \(\dfrac{π}{6}\), \( \dfrac{π}{4}\), \( \dfrac{π}{3}\), and \(\dfrac{π}{2}\). Therefore, the values of the other four trigonometric functions for these "special" angles can be found by using the reciprocal and quotient identities.

Example \(\PageIndex{6b}\): Finding the Trigonometric Functions of an Angle

Find \( \sin t, \cos t, \tan t, \sec t, \csc t, \) and \( \cot t\) when \(t=\dfrac{π}{6}\).

Solution

We have previously used the properties of equilateral triangles to demonstrate that \( \sin \left(\dfrac{π}{6}\right)=\dfrac{1}{2}\) and \( \cos \left(\dfrac{π}{6}\right) =\dfrac{\sqrt{3}}{2} \). We can use these values and the definitions of tangent, secant, cosecant, and cotangent as functions of sine and cosine to find the remaining function values.

\[ \begin{align*}
\tan \left(\dfrac{π}{6}\right) & = \dfrac{ \sin (\frac{π}{6})}{\cos(\frac{π}{6})} = \dfrac{\frac{1}{2} }{\frac{\sqrt{3}}{2}}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} 
\qquad &
\cot \left(\dfrac{π}{6}\right) & = \dfrac{ \cos (\frac{π}{6})}{ \sin (\frac{π}{6})} = \dfrac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} =\sqrt{3}  
\\
\sec \left(\dfrac{π}{6}\right) &= \dfrac{1}{ \cos (\frac{π}{6})} = \dfrac{1}{\frac{\sqrt{3}}{2}} = \dfrac{2}{\sqrt{3}}= \dfrac{2\sqrt{3}}{3} 
\qquad &
\csc \left(\dfrac{π}{6}\right) &= \dfrac{1}{ \sin (\frac{π}{6})}= \dfrac{1}{\frac{1}{2}}=2 
\end{align*}\]

A common mistake is that although \(\tan(\theta) = \dfrac{\sqrt{3}}{3} = \dfrac{\sin(\theta)}{\cos(\theta)} = 3\), it does NOT mean we can take \(\sin(\theta) = \sqrt{3}\) and \(\cos(\theta) = 3\). Instead, from \(\dfrac{\sin(\theta)}{\cos(\theta)} = \dfrac{\sqrt{3}}{3}\) we get: \(3\sin(\theta) = \sqrt{3} \cos(\theta)\).

Try It \(\PageIndex{6}\)

1. Find \(\sec\left(60^{\circ}\right)\)
2. Find \( \sin t,\; \cos t,\; \tan t,\; \sec t,\; \csc t,\;\) and \( \cot t\) when \(t=\dfrac{π}{3}\).

Answer

\(\text{1.} \quad \sec\left(60^{\circ}\right) = \dfrac{1}{\cos\left(60^{\circ}\right)}\). Hence, \(\sec\left(60^{\circ}\right) = \dfrac{1}{(1/2)} = 2\).

\(\text{2.} \;\; \sin \left(\dfrac{π}{3}\right) = \dfrac{\sqrt{3}}{2}, \;\; \cos \left(\dfrac{π}{3}\right) =\dfrac{1}{2}, \;\; \tan \left(\dfrac{π}{3}\right) = \sqrt{3}, \;\; \sec \left(\dfrac{π}{3}\right) = 2, \;\; \csc \left(\dfrac{π}{3}\right) = \dfrac{2\sqrt{3}}{3}, \;\; \cot \left(\dfrac{π}{3}\right) = \dfrac{\sqrt{3}}{3} \)

Because we know the sine and cosine values for the common first-quadrant angles, we can find the other four function values for those angles by rewriting the definitions of tangent, secant, cosecant, and cotangent in terms of sine and cosine and evaluating the resulting expressions. The results are shown in Table \(\PageIndex{1}\). It is worth taking the time to memorize the function values for at least the sine, cosine and tangent of the common 'special angles' listed in the table below.

Table \(\PageIndex{6}\) Values of Trigonometric functions of "Special Angles"

Angle	\(0\)	\(\dfrac{π}{6} \text{ or } 30°\)	\(\dfrac{π}{4} \text{ or } 45°\)	\(\dfrac{π}{3}\text{ or }60°\)	\(\dfrac{π}{2}\text{ or }90°\)
Sine	0	\(d\frac{1}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{\sqrt{3}}{2}\)	1
Cosine	1	\(\dfrac{\sqrt{3}}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{1}{2}\)	0
Tangent	0	\(\dfrac{\sqrt{3}}{3}\)	1	\(\sqrt{3}\)	Undefined
Cosecant	Undefined	2	\(\sqrt{2}\)	\(\dfrac{2\sqrt{3}}{3}\)	1
Secant	1	\(\dfrac{2\sqrt{3}}{3}\)	\(\sqrt{2}\)	2	Undefined
Cotangent	Undefined	\(\sqrt{3}\)	1	\(\dfrac{\sqrt{3}}{3}\)	0

Pythagorean Identities

The Pythagorean Identity we learned earlier was derived from the Pythagorean Theorem and the definitions of sine and cosine. We can build new identities from previously established identities. For example, if we divide both sides of the Pythagorean Identity by cosine squared, we can create a new identity:

\[\dfrac{\cos ^{2} (\theta )+\sin ^{2} (\theta )}{\cos ^{2} (\theta )} =\dfrac{1}{\cos ^{2} (\theta )}\nonumber\] Splitting the fraction on the left,
\[\dfrac{\cos ^{2} (\theta )}{\cos ^{2} (\theta )} +\dfrac{\sin ^{2} (\theta )}{\cos ^{2} (\theta )} =\dfrac{1}{\cos ^{2} (\theta )}\nonumber\] Simplifying and using the definitions of tangent and secant
\[1+\tan ^{2} (\theta )=\sec ^{2} (\theta ).\nonumber\]

Try It \(\PageIndex{7}\)

Use a similar approach to establish that \(\cot ^{2} (\theta )+1=\csc ^{2} (\theta )\).

Answer

\( 
\dfrac{\cos ^{2} (\theta )+\sin ^{2} (\theta )}{\sin ^{2} \theta }  = 1 \rightarrow 
\dfrac{\cos ^{2} (\theta )}{\sin ^{2} (\theta )} +\dfrac{\sin ^{2} (\theta )}{\sin ^{2} (\theta )}  = \dfrac{1}{\sin ^{2} (\theta )}  \rightarrow
\cot ^{2} (\theta )+1  = \csc ^{2} (\theta ) \)

Identities: Alternate forms of the Pythagorean Identity

\(\sin^2(\theta)+\cos ^{2} (\theta )=1\)          \(1+\tan ^{2} (\theta )=\sec ^{2} (\theta )\)          \(\cot ^{2} (\theta )+1=\csc ^{2} (\theta )\)

How to: Given one trigonometric ratio, find other ratios.

Identities Approach. Given a trigonometric ratio and other information.

1. Determine the quadrant the angle must be in, and thus the signs of the various trig ratios in that quadrant.
2. Use identities to find the other trig ratios and their appropriate signs.  Typically, use an identity to find the value of sine or cosine or their reciprocal functions, and then use other identities to find the rest of the trigonometric ratios. 

Given a Trigonometric Ratio and a Quadrant 

Example \(\PageIndex{8a}\)

If \(\tan (\theta )=\dfrac{2}{7}\) and \(\theta\) is in the 3\({}^{rd}\) quadrant, find \(\cos (\theta )\).

Solution

There are two approaches to this problem, both of which work equally well.

Approach 1 (Use the Pythagorean Theorem)

Angle \(\theta\) is in QIII where \(x < 0\) and \(y<0\).

\(\tan(\theta) = \dfrac{2}{7} = \dfrac{-2}{-7} = \dfrac{y}{x},\)  and because \(\theta\) is in QIII, \(x=-2\) and \(y=-7\)

Find \(r\) with the formula \(r=\sqrt{x^2+y^2} \Rightarrow r=\sqrt{(-2)^2+(-7)^2} \Rightarrow r=\sqrt{53}\).

Using the definitions, \( \cos (\theta )=\dfrac{x}{r} =\dfrac{-7}{\sqrt{53}} =-\dfrac{7\sqrt{53} }{53} \).

Approach 2 (Use Identities)

Use the \(1+\tan ^{2} (\theta )=\sec ^{2} (\theta )\) form of the Pythagorean Identity because we are given a tangent value,

\[ \begin{align*}
1+\tan ^{2} (\theta )&=\sec ^{2}(\theta ) && \text{ Use a Pythagorean Identity}\\[2 pt]
1+\left(\dfrac{2}{7} \right)^{2} &=\sec ^{2} (\theta ) && \text{ Substitute the known tangent value}\\[2 pt]
\dfrac{53}{49} &=\sec ^{2} (\theta ) \\[2 pt]
\sec (\theta ) &=\pm \sqrt{\dfrac{53}{49} } =\pm \dfrac{\sqrt{53} }{7}
\end{align*}\]

Since the angle is in the third quadrant, the cosine value will be negative so the secant value will also be negative. Keeping the negative result, and using definition of secant,

\[ \begin{align*}
\sec (\theta ) &=-\dfrac{\sqrt{53} }{7} \\[2 pt]
\cos (\theta ) &=-\dfrac{1}{\sec (\theta )} && \text{ Use the Reciprocal Identity for Secant}\\[2 pt]
\cos (\theta ) &=-\dfrac{1 }{\dfrac{\sqrt{53} }{7}} =-\dfrac{7}{\sqrt{53} } =-\dfrac{7\sqrt{53} }{53}  
\end{align*}\]

Example \(\PageIndex{8b}\): Using Identities to Relate Trigonometric Functions

Figure \(\PageIndex{8b}\)

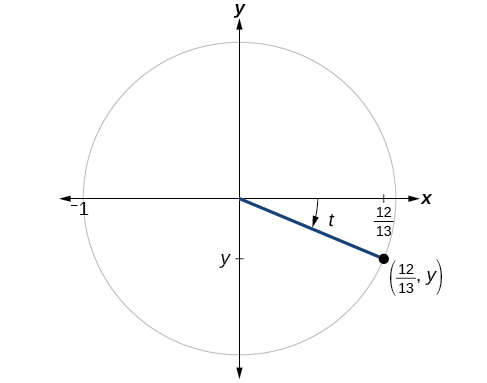
If \(\cos(t)=\dfrac{12}{13}\) and \(t\) is in quadrant IV, as shown in Figure \(\PageIndex{8b}\), find the values of the other five trigonometric functions.

Solution

We are given the value of cosine so we can find the sine using the Pythagorean Identity, \( \cos ^2 t+ \sin ^2t=1 \). Since the angle \(t\) is in the fourth quadrant, the sine ratio will be negative.

\[ \begin{align*} \left(\dfrac{12}{13}\right)^2+ \sin ^2 t &= 1 \\
\sin ^2 t &=1−\left(\dfrac{12}{13}\right)^2 =1− \dfrac{144}{169} \\
\sin ^2 t &= \dfrac{25}{169} \\
\sin t &=±\sqrt{\dfrac{25}{169}} =±\dfrac{\sqrt{25}}{\sqrt{169}} \\
\sin t &=± \dfrac{5}{13} = −\dfrac{5}{13} 
\nonumber \end{align*} \]

The remaining functions can be calculated using identities relating them to sine and cosine.

\( \tan t = \dfrac{\sin t}{ \cos t}=\dfrac{−\frac{5}{13}}{\frac{12}{13}}=−\dfrac{5}{12} \quad \sec t = \dfrac{1}{ \cos t}=\dfrac{1}{\frac{12}{13}}=\dfrac{13}{12} \\  \csc t = \dfrac{1}{\sin t}=\dfrac{1}{−\frac{5}{13}} =−\dfrac{13}{5} \quad \cot t = \dfrac{1}{ \tan t}=\dfrac{1}{−\frac{5}{12}}=−\dfrac{12}{5} \)

Try It \(\PageIndex{8}\)

Evaluate \(\cos\left(\theta\right)\), where \(\csc(\theta) = -\sqrt{5}\) and \(\theta\) is a Quadrant IV angle.

Answer

Given \(\csc(\theta)  = -\sqrt{5}\), use the Reciprocal Identity \(\sin(\theta) = -\frac{1}{\csc (\theta)} \) to obtain \(\sin(\theta) = -\frac{1}{\sqrt{5}} = -\frac{\sqrt{5}}{5}\). Use the Pythagorean Identity, \(\cos^{2}(\theta) + \sin^2(\theta) = 1,\)  to find \(\cos(\theta)\). Substituting, we get \(\cos^{2}(\theta) + \left(-\frac{\sqrt{5}}{5}\right)^2 = 1\), which gives \(\cos^{2}(\theta) +\frac{5}{25}. \) Therefore,  \(\cos^{2}(\theta) = \frac{4}{5}\), or \(\cos(\theta) = \pm \frac{2 \sqrt{5}}{5}\). Since \(\theta\) is a Quadrant IV angle, \(\cos(\theta) > 0\), so \(\cos(\theta) = \frac{2 \sqrt{5}}{5}\)

Trigonometric Function Values from Reference Angles

Figure \(\PageIndex{9}\) Quadrants where
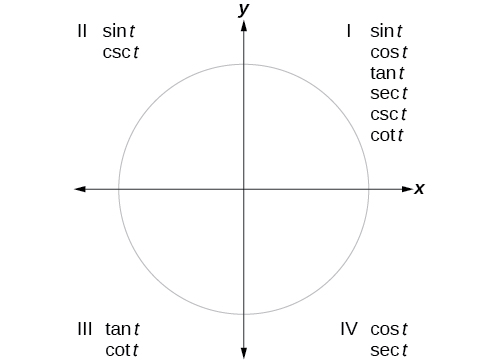
trigonometric functions are positive 

We can evaluate trigonometric functions of angles outside the first quadrant using reference angles as we have already done with the sine and cosine functions. The procedure is the same: Find the reference angle formed by the terminal side of the given angle with the horizontal axis. The trigonometric function values for the original angle will be the same as those for the reference angle, except for the positive or negative sign, which is determined by x- and y-values in the quadrant where the terminal side is located.

Figure \(\PageIndex{9}\) shows which functions are positive in which quadrant. 

To help us remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase “All Students Take Classes.” Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is “A,” all of the six trigonometric functions are positive. In quadrant II, “Students,” only sine and its reciprocal function, cosecant, are positive. In quadrant III, “Take,” only tangent and its reciprocal function, cotangent, are positive. Finally, in quadrant IV, “Classes,” only cosine and its reciprocal function, secant, are positive.

Example \(\PageIndex{9}\): Coterminal Angles and Reference Angles

Let \(\theta = 928^\circ \).

1. Which angle between \(0^\circ \) and \(360^\circ \) has the the same trigonometric function values as \(\theta\,\)?
2. What is the reference angle for \(\theta\,\)?
3. Draw these angles in standard position.

Solution

(a) Since \(928^\circ = 2 \times 360^\circ + 208^\circ, \) \(\theta \) has the same terminal side as \(208^\circ \), and thus the angles \(928^\circ \) and \( 208^\circ\) are coterminal. This is illustrated in Figure \(\PageIndex{9a}\). Therefore,  \(208^\circ \) has the same trigonometric function values as \(\theta = 928^\circ \).    (b) \(928^\circ \) and \(208^\circ \) have the same terminal side in QIII, so the reference angle for \(\theta = 928^\circ \) is \(208^\circ - 180^\circ = 28^\circ \).

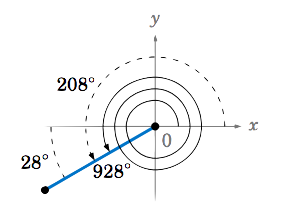Figure \(\PageIndex{9a}\)

Generalized Reference Angle Theorem

The absolute value of trigonometric functions of an angle \(\theta\), are the same as the corresponding trigonometric functions of its reference angle \(\alpha\). More specifically, if \(\alpha\) is the reference angle for an \(\theta\), then:

\(\sin(\theta) = \pm \sin(\alpha)\) \(\csc(\theta) = \pm \csc(\alpha)\)

\(\cos(\theta) = \pm \cos(\alpha)\) \(\sec(\theta) = \pm \sec(\alpha)\)

\(\tan(\theta) = \pm \tan(\alpha)\) \(\cot(\theta) = \pm \cot(\alpha)\)

The choice of the (\(\pm\)) depends on the quadrant in which the terminal side of \(\theta\) lies.

How to: Find Trigonometric Functions using Reference Angles.

1. Measure the angle formed by the terminal side of the given angle and the horizontal axis. This is the reference angle. The measure of a reference angle is ALWAYS a positive number between \(0\) and \(\frac{\pi}{2}\)
2. Observe the quadrant where the terminal side of the original angle is located. Based on the quadrant, determine whether the output is positive or negative. Rewrite the function in terms of the reference angle and the appropriate sign.
3. Evaluate the function at the reference angle.

Example \(\PageIndex{10}\): Using Reference Angles to Find Trigonometric Functions

Use reference angles to find all six trigonometric functions of \(−\dfrac{5π}{6}\).

Solution

The angle between this angle’s terminal side and the x-axis is \(\dfrac{π}{6}\), so that is the reference angle. Since \(−\dfrac{5π}{6}\) is in the third quadrant, where both \(x\) and \(y\) are negative, then sine, cosine, secant, and cosecant will be negative, while tangent and cotangent will be positive.

\(\sin \left(−\dfrac{5π}{6} \right) = - \sin \left(  \dfrac{π}{6}  \right)= −\dfrac{1}{2} \)	\(\cos \left(−\dfrac{5π}{6} \right) = - \cos \left(   \dfrac{π}{6}  \right) = −\dfrac{\sqrt{3}}{2} \)	\(\tan \left(−\dfrac{5π}{6} \right) = + \tan \left(   \dfrac{π}{6}   \right) = \dfrac{\sqrt{3}}{3} \)
\(\csc \left(−\dfrac{5π}{6} \right) = -\csc \left(   \dfrac{π}{6}   \right) = −2 \)	\(\sec \left(−\dfrac{5π}{6} \right) = - \sec \left(   \dfrac{π}{6}   \right) = −\dfrac{2\sqrt{3}}{3} \)	\(\cot \left(−\dfrac{5π}{6} \right) = + \cot \left(   \dfrac{π}{6}  \right) = \sqrt{3} \)

Try It \(\PageIndex{10}\)

Use reference angles to find all six trigonometric functions of \(−\dfrac{7π}{4}\).

Answer

Angle \(−\dfrac{7π}{4}\) is in QI where all trigonometric functions are positive.

\( \sin \left(−\frac{7π}{4} \right) = \frac{\sqrt{2}}{2}, \; \cos \left(−\frac{7π}{4}\right) = \frac{\sqrt{2}}{2}, \; \tan \left(−\frac{7π}{4}\right) = 1, \; \csc \left(−\frac{7π }{4}\right) = \sqrt{2}, \; \sec \left(−\frac{7π}{4}\right) = \sqrt{2}, \; \cot \left(−\frac{7π}{4}\right) =1 \)

Example \(\PageIndex{11}\)

Use Identities to determine the exact value of each of the following function values.

1. \(\sec \left(\dfrac{7\pi}{4}\right) \) \( \qquad \qquad \) 2. \(\csc \left(\dfrac{7\pi }{6} \right)\)  \( \qquad \qquad \) 3. \(\tan\left(\theta\right)\), where \(\theta\) is any angle coterminal with \(\dfrac{3\pi}{2}\).

Solution 

\( \begin{align*}
1. \quad & \sec\left(\dfrac{7\pi}{4}\right) &&= \dfrac{1}{\cos\left(\dfrac{7\pi}{4}\right)} = \dfrac{1}{ + \cos\left( \dfrac{\pi}{4} \right)} = \dfrac{1}{\frac{\sqrt{2}}{2}} = \dfrac{2}{\sqrt{2}} = \sqrt{2} &&  \text{  in QIV so \(x\) and cos positive} \\
2. \quad & \csc \left(\dfrac{7\pi }{6} \right) &&= \dfrac{1}{\sin\left(\dfrac{7\pi }{6} \right)} = \dfrac{1}{ - \sin\left( \dfrac{\pi }{6} \right)} = \dfrac{1}{-1/2} = -2 &&  \text{ in QIII so \(y\) and sine negative}
\end{align*}\)

 \( \begin{align*}
3. \quad & \tan \left(\theta\right) &&= \tan \left(\dfrac{3\pi}{2}\right) = \dfrac{\sin \left(\dfrac{3\pi}{2}\right) }{\cos\left(\dfrac{3\pi}{2}\right) }= \dfrac{-1}{0} = \text{ Undefined} \\ 
                               &\text{Or } && = \tan \left(\dfrac{3\pi}{2}\right) = \pm \tan \left(\dfrac{\pi}{2}\right)=  \text{Undefined}&& \pm\text{undefined is undefined}
\end{align*}\)

Try It \(\PageIndex{11}\)

Use Identities to determine the exact value of each of the following function values.

1. \( \csc\left(\dfrac{-\pi}{4}\right) \)  \( \qquad \qquad \)  2. \( \cot\left(\dfrac{4\pi}{3}\right) \)

Answer

\[ \begin{align*}
1. \quad & \csc\left(\dfrac{-\pi}{4}\right) &&= \dfrac{1}{\sin\left(\dfrac{-\pi}{4}\right)} = \dfrac{1}{-\sin\left(\dfrac{\pi}{4}\right)} = \dfrac{1}{-\frac{\sqrt{2}}{2}} = -\dfrac{2}{\sqrt{2}} = -\sqrt{2} && \text{ in QIV so \(y\) & sine neg.} \\
2. \quad & \cot\left(\dfrac{4\pi}{3}\right) &&= \dfrac{\cos\left(\dfrac{4\pi}{3}\right)}{\sin\left(\dfrac{4\pi}{3}\right)}= \dfrac{-\cos\left(\dfrac{\pi}{3}\right)}{-\sin\left(\dfrac{\pi}{3}\right)} = \dfrac{1/2}{\sqrt{3}/2}= \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3}&& \text{ in QIII so sine & cos neg.} \\
 &\text{Or } && = \dfrac{1}{ \tan\left(\dfrac{4\pi}{3}\right) } =  \dfrac{1}{ +  \tan\left(\dfrac{\pi}{3}\right) }= \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3}
\end{align*}\]

Trigonometric Function Values from a Calculator

Values for the six trigonometric functions of "special" first-quadrant angles, and multiples of these angles that lie in other quadrants, can be evaluated using the value of the trig function for its reference angle and modifying the sign when appropriate.

For other angles, a calculator can be used to evaluate trigonometric functions. If the calculator has degree mode and radian mode, confirm the correct mode is chosen before making a calculation. There are calculator keys for SIN, COS, and TAN, but typically not for CSC, SEC, or COT. To evaluate these last three functions, the function must be evaluated as the reciprocal of a sine, cosine, or tangent function.

Example \(\PageIndex{12}\): Evaluating the Cosecant Using Technology

1. Use a calculator to find the cosecant of \(\dfrac{5π}{7}\). \( \qquad \qquad \) Use a calculator to find the secant of \( 30°\).

1. Solution

• The angle is in radians so be sure the calculator is in radian mode.
• There is not a cosecant button on the calculator, so the reciprocal identity \(\csc (\theta )=\dfrac{1}{\sin (\theta )}\) must be used.
• Enter the following keystrokes: \(\mathrm{1 ÷ ( SIN( 5 × π ÷ 7 ) ) \; ENTER}\).
• The result obtained is \(1.2790480...\)

2. Solution

• The angle is in degrees so be sure the calculator is in degree mode.
• Enter the following keystrokes: \(\mathrm{1 ÷ COS( 30 ) \; ENTER}\).
• The result is \(1.15470053...\)
• If the calculator does not have a degree mode, the angle must also be converted to radians. When the calculator only has a radian mode, enter the following keystrokes: \(\mathrm{1 ÷ COS( 30 × π ÷ 180) \; ENTER}.\)

Try It \(\PageIndex{12}\)

Use a calculator to evaluate the following. Round to four decimal digits.

1. \(\sec \left(\dfrac{7\pi}{8}\right) \qquad \) 2. \(\csc \left(−\frac{π}{8} \right) \qquad \) 3.  \(\cot(3)\)

Answer

\(\sec \left(\dfrac{7\pi}{8}\right) = \dfrac{1}{ \cos \left(\dfrac{7\pi}{8}\right)} \approx -1.0824 \qquad
\csc \left(−\dfrac{π}{8} \right) = \dfrac{1}{ \sin \left(−\dfrac{π}{8} \right)} \approx -2.6131 \qquad
\cot(3) = \dfrac{1}{\tan(3)} \approx -7.015 \)

Even and Odd Trigonometric Functions

To be able to use our six trigonometric functions freely with both positive and negative angle inputs, we should examine how each function treats a negative input. As it turns out, there is an important difference among the functions in this regard. Recall in Section 2.2: Attributes of Functions, even and odd functions were defined. This definition is repeated here.

Definition: Odd and Even functions

• An even function is one in which \(f(−x)=f(x)\). An even function has \(y\)-axis symmetry.
• An odd function is one in which \(f(−x)=−f(x)\). An odd function has origin axis symmetry.

Figure \(\PageIndex{13}\)

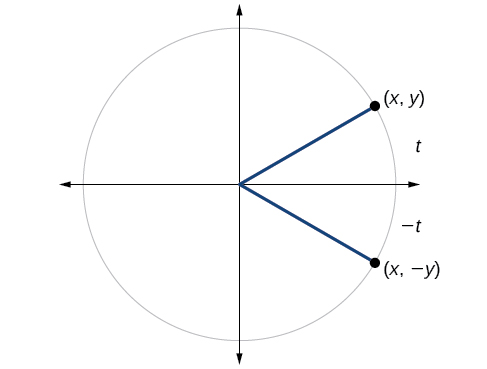
We can test whether a trigonometric function is even or odd by drawing a unit circle with a positive and a negative angle, as illustrated in Figure \(\PageIndex{13}\).

• The sine of the positive angle is \(\sin (t) = \dfrac{y}{r}\). The sine of the negative angle is \(\sin (-t) = \dfrac{-y}{r}= - \dfrac{y}{r}\). Thus, \( \sin (-t) = - \sin (t) \) and the sine function is an odd function.
• The cosine of the positive angle is \(\cos (t) = \dfrac{x}{r}\). The cosine of the negative angle is \(\cos (-t) = \dfrac{x}{r}\). Thus, \( \cos (-t) = \cos (t) \) and the cosine function is an even function.
• The tangent of the positive angle is \(\tan (t) = \dfrac{y}{x}\). The tangent of the negative angle is \(\tan (-t) = \dfrac{-y}{x}= - \dfrac{y}{x}\). Thus, \( \tan (-t) = - \tan (t) \) and the tangent function is an odd function.

Similar arguments can be made for the secant, cosecant and cotangent functions.

Even and Odd Trigonometric Functions; Even/Odd Identities

Cosine and secant are even functions:

\[ \begin{align*} \cos (−t) &= \cos t \\ \sec (−t) &= \sec t \end{align*}\]

Sine, tangent, cosecant, and cotangent are odd functions:

\[\begin{align*} \sin (−t) &=− \sin t \qquad & \tan (−t) &=−\tan t \\ \csc (−t) &=−\csc t & \cot (−t) &=−\cot t \end{align*}\]

Example \(\PageIndex{13}\): Using Even and Odd Properties of Trigonometric Functions

If  \( \sec t = 2 \), what is \( \sec(−t) \)?

Solution

Secant is an even function. The secant of an angle is the same as the secant of its opposite. So if the secant of angle t is 2, the secant of \(−t\) is also 2.

 

Try It \(\PageIndex{13}\)

If the cotangent of angle \(t\) is \(\sqrt{3}\), what is the cotangent of \(−t?\)

Answer

\(−\sqrt{3}\)

Cofunction Identities

Figure \(\PageIndex{14a}\): The sine of \(\frac{π}{3}\) equals
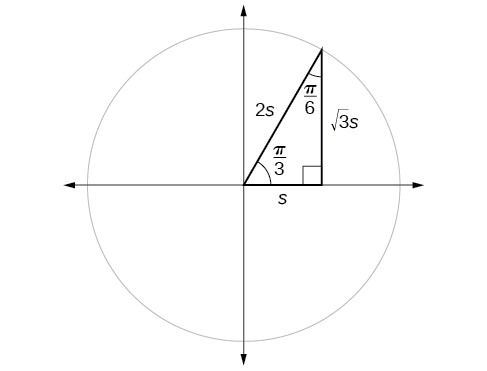
the cosine of \(\frac{π}{6}\) and vice versa.

If we look more closely at the relationship between the sine and cosine of the special angles relative to the unit circle, we will notice a pattern. In a right triangle with angles of \(\frac{π}{6}\) and \(\frac{π}{3}\), we see that the sine of \(\frac{π}{3}\), namely \(\frac{\sqrt{3}}{2}\), is also the cosine of \(\frac{π}{6}\), while the sine of \(\frac{π}{6}\), namely \(\frac{1}{2},\) is also the cosine of \(\frac{π}{3}\) (Figure \(\PageIndex{14a}\)).

\[\begin{align*} \sin \frac{π}{3} &= \cos \frac{π}{6}=\frac{\sqrt{3}s}{2s}=\frac{\sqrt{3}}{2} \\ \sin \frac{π}{6} &= \cos \frac{π}{3}=\frac{s}{2s}=\frac{1}{2} \end{align*}\]

This result should not be surprising because, as we see from Figure \(\PageIndex{14a}\), the side opposite the angle of \(\frac{π}{3}\) is also the side adjacent to \(\frac{π}{6}\), so \(\sin (\frac{π}{3})\) and \(\cos (\frac{π}{6})\) are exactly the same ratio of the same two sides, \(\sqrt{3} s\) and \(2s.\) Similarly, \( \cos (\frac{π}{3})\) and \( \sin (\frac{π}{6})\) are also the same ratio using the same two sides, \(s\) and \(2s\).

Figure \(\PageIndex{14b}\): Cofunction identity

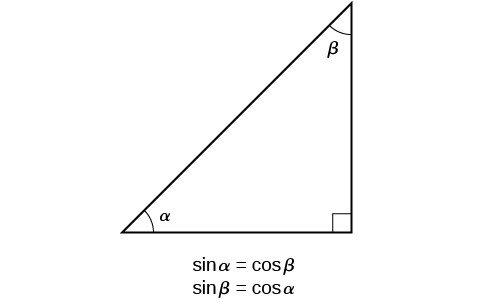
The interrelationship between the sines and cosines of \(\frac{π}{6}\) and \(\frac{π}{3}\) also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to π, and the right angle is \(\frac{π}{2}\), the remaining two angles must also add up to \(\frac{π}{2}\). That means that a right triangle can be formed with any two angles that add to \(\frac{π}{2}\)—in other words, any two complementary angles. So we may state a cofunction identity: If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in Figure \(\PageIndex{14b}\).

Using this identity, we can state without calculating, for instance, that the sine of \(\frac{π}{12}\) equals the cosine of \(\frac{5π}{12}\), and that the sine of \(\frac{5π}{12}\) equals the cosine of \(\frac{π}{12}\). We can also state that if, for a certain angle \(t, \cos t= \frac{5}{13},\) then \( \sin (\frac{π}{2}−t)=\frac{5}{13}\) as well.

Cofunction Identities

The cofunction identities in terms of radians are listed below.

\( \sin (t) = \cos \left(\dfrac{π}{2}−t \right) \)	\( \cos (t) = \sin \left(\dfrac{π}{2}−t\right) \)	\( \tan (t) = \cot \left(\dfrac{π}{2}−t\right) \)
\( \csc (t) = \sec \left(\dfrac{π}{2}−t\right) \)	\( \sec (t) = \csc \left(\dfrac{π}{2}−t\right) \)	\( \sec (t) = \csc \left(\dfrac{π}{2}−t\right) \)

Example \(\PageIndex{14}\): Using Cofunction Identities

If \( \sin (t) = \dfrac{5}{12},\) find \( \cos  \left( \dfrac{π}{2}−t  \right) \).

Solution

According to the cofunction identities for sine and cosine, \( \sin (t) = \cos \left(\dfrac{π}{2}−t\right) . \) So \( \cos \left(\dfrac{π}{2}−t\right) = \dfrac{5}{12}. \)

Try It \(\PageIndex{14}\)

If \(\csc \left(\dfrac{π}{6} \right)=2,\) find \( \sec \left(\dfrac{π}{3} \right) .\)

Answer

2

Key Equations

Tangent function	\( \tan t= \dfrac{ \sin t}{\cos t}\)
Secant function	\( \sec t= \dfrac{1}{ \cos t}\)
Cosecant function	\( \csc t= \dfrac{1}{ \sin t}\)
Cotangent function	\( \cot t= \dfrac{1}{\tan t}= \dfrac{\cos t}{ \sin t}\)

Reciprocal Identities	\(\csc (\theta )=\dfrac{1}{\sin (\theta )}\) \(\sin (\theta )=\dfrac{1}{\csc (\theta )}\)	\(\sec (\theta )=\dfrac{1}{\cos (\theta )}\) \(\cos (\theta )=\dfrac{1}{\sec (\theta )}\)	\(\cot (\theta )=\dfrac{1}{\tan (\theta )}\) \(\tan (\theta )=\dfrac{1}{\cot (\theta )}\)
Quotient Identities	\(\tan (\theta )=\dfrac{\sin (\theta )}{\cos (\theta )}\)	\(\cot (\theta )=\dfrac{\cos (\theta )}{\sin (\theta )}\)
Pythagorean Identities	\( \sin^2(\theta )+\cos^2 (\theta) =1 \)	\(1+\tan ^{2} (\theta )=\sec ^{2} (\theta )\)	\(\cot ^{2} (\theta )+1=\csc ^{2} (\theta )\)
Even/Odd Identities	\( \sin (−t) =− \sin t \\  \csc (−t) =−\csc t  \)	\(\cos (−t) = \cos t \\ \sec (−t) = \sec t \)	\(  \tan (−t)  =−\tan t \\  \cot (−t) =−\cot t \)
Cofunction Identities	\( \sin t = \cos (\frac{π}{2}−t) \)  \( \cos t = \sin ( \frac{π}{2}−t) \)	\( \sec t = \csc (\frac{π}{2}−t) \)  \( \csc t = \sec (\frac{π}{2}−t) \)	\( \tan t = \cot (\frac{π}{2}−t) \) \(  \cot t = \tan (\frac{π}{2}−t) \)

Key Concepts

• The tangent of an angle is the ratio of the y-value to the x-value of the corresponding point on the unit circle.
• The secant, cotangent, and cosecant are all reciprocals of other functions. The secant is the reciprocal of the cosine function, the cotangent is the reciprocal of the tangent function, and the cosecant is the reciprocal of the sine function.
• The six trigonometric functions can be found from a point on the unit circle.
• Trigonometric functions can also be found from an angle.
• Trigonometric functions of angles outside the first quadrant can be determined using reference angles.
• The Pythagorean Identity makes it possible to find a cosine from a sine or a sine from a cosine.
• Identities can be used to evaluate trigonometric functions.
• Fundamental identities such as the Pythagorean Identity can be manipulated algebraically to produce new identities.
• The values of trigonometric functions of special angles can be found by mathematical analysis.
• To evaluate trigonometric functions of other angles, we can use a calculator or computer software.
• A function is said to be even if \(f(−x)=f(x)\) and odd if \(f(−x)=−f(x)\).
• Cosine and secant are even; sine, tangent, cosecant, and cotangent are odd.
• Even and odd properties can be used to evaluate trigonometric functions.

Glossary

cosecant

the reciprocal of the sine function: on the unit circle, \( \csc t=\frac{1}{y},y≠0\),  or more generally \( \csc t=\frac{r}{y},y≠0\)

cotangent

the reciprocal of the tangent function: on the unit circle, \( \cot t= \frac{x}{y},y≠0\) 

identities

statements that are true for all values of the input on which they are defined

secant

the reciprocal of the cosine function: on the unit circle, \( \sec t= \frac{1}{x},x≠0 \),  or more generally \( \sec t= \frac{r}{x},x≠0 \)

tangent

the quotient of the sine and cosine: on the unit circle, \( \tan t= \frac{y}{x},x≠0\)

Contributors and Attributions

• Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.