5.4e: Exercises - Other Trigonometric Functions

A: Concepts

Exercise $\PageIndex{A}$

1) On an interval of $[ 0,2π )$, can the sine and cosine values of a radian measure ever be equal? If so, where?

2) What would you estimate the cosine of $\pi$ degrees to be? Explain your reasoning.

3) For any angle in quadrant II, if you knew the sine of the angle, how could you determine the cosine of the angle?

4) Describe the secant function.

Answers to Odd Problems

1. Yes, when the reference angle is $\dfrac{π}{4}$ and the terminal side of the angle is in quadrants I and III. Thus, at $x=\dfrac{π}{4},\dfrac{5π}{4}$, the sine and cosine values are equal.
3. Substitute the sine of the angle in for $y$ in the Pythagorean Theorem $x^2+y^2=1$. Solve for $x$ and take the negative solution.

B: Given a point

Exercise $\PageIndex{B}$ 

$\bigstar$ Given the following point on the terminal side of an angle $\theta$, find the value of each of the six trigonometric functions.

5.   $(\sqrt{5}, 2 )$

6.   $(-4, \sqrt{2} )$

7.   $(-1, -\sqrt{7})$

8.   $(2\sqrt{3}, -5 )$

$\bigstar$ For the below, use the angle in the unit circle to find the value of each of the six trigonometric functions.

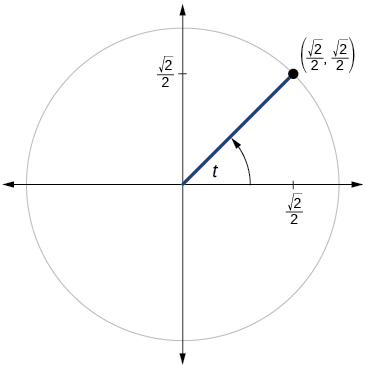
9.

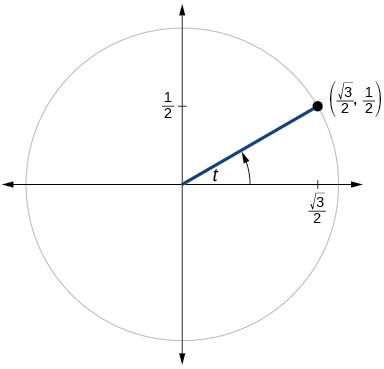
10.

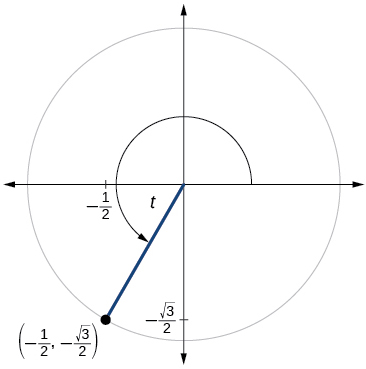
11.

Answers to Odd Problems

5. $\sin \theta = \frac{2}{3},$    $\cos \theta = \frac{\sqrt{5}}{3},$    $\tan \theta = \frac{2\sqrt{5}}{5},$    $\csc \theta = \frac{3}{2},$    $\sec \theta = \frac{3\sqrt{5}}{5},$   $\cot \theta = \frac{\sqrt{5}}{2}$
7. $\sin \theta =- \frac{\sqrt{14}}{4},$    $\cos \theta = -\frac{\sqrt{2}}{4},$    $\tan \theta = \sqrt{7},$    $\csc \theta = - \frac{2\sqrt{14}}{7},$    $\sec \theta = -2\sqrt{2},$   $\cot \theta = \frac{\sqrt{7}}{7}$
9. $\sin t= \frac{\sqrt{2}}{2},$    $\cos t= \frac{\sqrt{2}}{2},$    $\tan t=1,$    $\cot t=1,$    $\sec t= \sqrt{2},$    $\csc t=  \sqrt{2}$
11. $\sin t=−\frac{\sqrt{3}}{2},$    $\cos t=−\frac{1}{2},$    $\tan t=\sqrt{3},$    $\cot t= \frac{\sqrt{3}}{3},$    $\sec t=−2,$    $\csc t=−\frac{2\sqrt{3}}{3}$

C: Get information about an angle from the sign of its trigonometric ratio

Exercise $\PageIndex{C}$

$\bigstar$ State the quadrant or quadrants for which the following conditions are true.

15.  Sine and cosine have the same sign. 16.  Sine and cosine have the opposite sign. 17.  Sine and tangent have the same sign.

18.  Sine and tangent have the opposite sign. 19.  Cosine and tangent have the same sign. 20.  Cosine and tangent have the opposite sign.

Answers to Odd Problems

15.  QI  or QIII    17.  QI or QIV     19.   QI or QII 

D: Given one ratio and information to find which quadrant the angle is in

Exercise $\PageIndex{D}$

Given one trigonometric ratio and information about the angle, find the other five trigonometric ratios.

21. $\sin \left(\theta \right)=\dfrac{3}{4}$,  $\theta$ in quadrant II 22. $\csc \left(\theta \right)= - \dfrac{7}{2}$, $\theta$ in quadrant IV 23. $\cos \left(\theta \right)=-\dfrac{1}{3}$, $\theta$ in quadrant III 24. $\sec \left(\theta \right)= -5$,  $\theta$ in quadrant II

25. $\tan \left(\theta \right)=\dfrac{12}{5}$,  $\pi \le \theta <\dfrac{3\pi }{2}$ 26. $\cot \left(\theta \right)= -4$,  $\dfrac{\pi }{2} \le \theta < \pi$ 27. $\sec \left(\theta \right)= -7$,  $\dfrac{\pi }{2} < \theta < \pi$ 28. $\csc \left(\theta \right)= - \dfrac{7}{3}$,  $\pi \le \theta <\dfrac{3\pi }{2}$

29. $\cot \left(\theta \right)= -\dfrac{4}{3}$,  $\csc \theta < 0$ 30. $\tan \left(\theta \right)= - 7$,  $\sec \theta > 0$ 31. $\csc \left(\theta \right)= 4$,  $\cot \theta < 0$ 32. $\sec \left(\theta \right)=\dfrac{5}{2}$,  $\sin \theta < 0$

Answers to Odd Problems

21. $\cos(\theta) = -\frac{\sqrt{7}}{4}$, $\tan(\theta) = -\frac{3\sqrt{7}}{7}$, $\csc(\theta) = \frac{4}{3}$, $\sec (\theta) = -\frac{4\sqrt{7}}{7}$, $\cot(\theta) = -\frac{\sqrt{7}}{3}$

23. $\sin(\theta) = -\frac{2\sqrt{2}}{3}$, $\tan(\theta) = 2\sqrt{2}$, $\csc(\theta) = -\frac{3\sqrt{2}}{4}$, $\sec(\theta) = -3$, $\cot(\theta) = \frac{\sqrt{2}}{4}$ 

25. $\sin(\theta) =- \frac{12}{13}$, $\cos(\theta) =- \frac{5}{13}$, $\csc(\theta) = -\frac{13}{12}$, $\sec(\theta) = -\frac{13}{5}$, $\cot(\theta) = \frac{5}{12}$

27. $\sin(\theta) = \frac{4\sqrt{3}}{7}, \;$ $\cos(\theta) = -\frac{1}{7}, \;$ $\tan(\theta) = -4\sqrt{3}, \;$ $\csc(\theta) = \frac{7\sqrt{3}}{12}, \;$ $\sec(\theta) = -7, \;$ $\cot(\theta) = -\frac{\sqrt{3}}{12}$

29. $\sin(\theta) =- \frac{3}{5}, \;$ $\cos(\theta) = \frac{4}{5}, \;$ $\tan(\theta) = -\frac{3}{4}, \;$ $\csc(\theta) = -\frac{5}{3}, \;$ $\sec(\theta) = \frac{5}{4}, \;$ $\cot(\theta) = -\frac{4}{3}$

31. $\sin(\theta) = \frac{1}{4}, \;$ $\cos(\theta) =- \frac{\sqrt{15}}{4}, \;$ $\tan(\theta) = -\frac{\sqrt{15}}{15}, \;$ $\csc(\theta) = 4, \;$ $\sec(\theta) = -\frac{4\sqrt{15}}{15}, \;$ $\cot(\theta) = -\sqrt{15}$

E: Find quadrants or axes where a ratio is the same; find other ratios for each location

Exercise $\PageIndex{E}$

$\bigstar$ Find the quadrants or axes and exact values of $\sin\;\theta$ and $\tan\;\theta$ when $\cos\;\theta$ has the indicated value

41.  $\cos\;\theta = \dfrac{1}{2}$

42.  $\cos\;\theta = -\dfrac{1}{2}$

43.  $\cos\;\theta = 0$

44.  $\cos\;\theta = \dfrac{2}{5}$

45.  $\cos\;\theta = 1$

$\bigstar$ Find the quadrants or axes and the exact values of $\cos\;\theta$ and $\tan\;\theta$ when $\sin\;\theta$ has the indicated value.

46.  $\sin\;\theta = \dfrac{1}{2}$

47.  $\sin\;\theta = -\dfrac{1}{2}$

48.  $\sin\;\theta = 0$

49.   $\sin\;\theta = -\dfrac{2}{3}$

50.  $\sin\;\theta = 1$

$\bigstar$ Find the quadrants or axes and the exact values of $\sin\;\theta$ and $\cos\;\theta$ when $\tan\;\theta$ has the indicated value.

51.  $\tan\;\theta = \dfrac{1}{2}$

52.  $\tan\;\theta = -\dfrac{1}{2}$

53.  $\tan\;\theta = 0$

54.  $\tan\;\theta = \dfrac{5}{12}$

55.  $\tan\;\theta = 1$

Answers to Odd Problems:

41.  QI: $\sin \theta = \frac{\sqrt{3}}{2},$ $\tan \theta = \sqrt{3}$    or    QIV: $\sin \theta = -\frac{\sqrt{3}}{2},$ $\tan \theta = -\sqrt{3}$
43.  positive $y$-axis: $\sin \theta = 1,$ $\tan \theta$ = undefined   or  negative $y$-axis: $\sin \theta = -1,$ $\tan \theta$ = undefined
45.  positive $x$-axis: $\sin \theta = 0,$ $\tan \theta = 0$   or  negative $x$-axis: $\sin \theta = 0,$ $\tan \theta = 0$
47.  QIII: $\cos \theta =  -\frac{\sqrt{3}}{2},$ $\tan \theta = \frac{\sqrt{3}}{3}$    or    QIV: $\cos \theta =  \frac{\sqrt{3}}{2},$ $\tan \theta = -\frac{\sqrt{3}}{3}$
49.  QIII: $\cos \theta =  -\frac{\sqrt{5}}{3},$ $\tan \theta = \frac{2\sqrt{5}}{5}$    or    QIV: $\cos \theta =  \frac{\sqrt{5}}{3},$ $\tan \theta = -\frac{2\sqrt{5}}{5}$
51.  QI: $\sin \theta = \frac{\sqrt{5}}{5},$  $\cos \theta =  \frac{2\sqrt{5}}{5}$   or    QIII: $\sin \theta = -\frac{\sqrt{5}}{5},$  $\cos \theta =  -\frac{2\sqrt{5}}{5}$
53.  positive $x$-axis: $\sin \theta = 0,$ $\cos \theta = 1$   or  negative $x$-axis: $\sin \theta = 0,$ $\cos \theta = -1$
55.   QI: $\sin \theta = \frac{\sqrt{2}}{2},$  $\cos \theta =  \frac{\sqrt{2}}{2}$   or    QIII: $\sin \theta = -\frac{\sqrt{2}}{2},$  $\cos \theta =  -\frac{\sqrt{2}}{2}$

F: Use identities to find other trig ratios from two given ratios

Exercise $\PageIndex{F}$ 

61. If $\sin t= \dfrac{\sqrt{3}}{2}$ and $\cos t=\dfrac{1}{2},$ find $\sec t, \csc t, \tan t,$ and $\cot t$.

62. If $\sin 40°≈0.643 \; \cos 40°≈0.766 \; \sec 40°,\csc 40°,\tan 40°, \text{ and } \cot 40°$.

63. If $\tan (t)≈1.3,$ and $\cos (t)≈0.61$, find $\sin (t)$.

64. If $\tan (t)≈2.7,$ and $\sin (t)≈0.94,$ find $\cos (t)$.

65. If $\cot (t)≈0.58,$ and $\cos (t)≈0.5,$ find $\csc (t)$.

66. If $\csc (t)≈3.2,$ and  $\cos (t)≈0.95,$ find $\tan (t)$.

67. Use identities to simplify $\dfrac{\sec t}{ \csc t}$

68. Use identities to simplify $\csc t \tan t$

70. Use the given information and identities to find the value of the other five trigonometric functions

a. $\sin \left(\theta \right)= - \dfrac{1}{3}$,  $\theta$ in quadrant IV b. $\csc \left(\theta \right)=  \dfrac{5}{3}$, $\theta$ in quadrant I

c. $\cos \left(\theta \right)= \dfrac{1}{4}$, $\theta$ in quadrant IV d. $\sec \left(\theta \right)= -4$,  $\theta$ in quadrant II

e. $\tan \left(\theta \right)= 5$, $\theta$ in quadrant III f. $\cot \left(\theta \right)=- \dfrac{1}{6}$,  $\theta$ in quadrant II

Answers to Odd Problems:

61. $\sec t=2, \csc t=\frac{2\sqrt{3}}{3}, \tan t= \sqrt{3}, \cot t= \frac{\sqrt{3}}{3}$    63. $\sin (t)≈0.79$ $\quad$ 65. $\csc (t)≈1.16$  67. $\tan t$.

G: Quadrants and Reference angles

Exercise $\PageIndex{G}$

$\bigstar$ State in which quadrant or on which axis the given angle lies.

71.  $127^\circ$ 72.  $-127^\circ$

73.   $313^\circ$ 74.  $-313^\circ$

75.  $-90^\circ$ 76.  $621^\circ$

77.   $230^\circ$ 78.  $2009^\circ$

79.  $1079^\circ$ 80  $-514^\circ$

$\bigstar$ Find the reference angle for the given angle.

81.  $317^\circ$

82.  $63^\circ$

83.  $-126^\circ$

84.  $696^\circ$

85.  $275^\circ$

Answers to Odd Problems:

71.   QII      73.   QIV     75.   on negative $y$-axis     77.   QIII     79.   QIV     81.  $43^\circ$     83.  $54^\circ$     85.   $85^\circ$ 

H: Evaluate trig ratios for Multiples of "Special" Angles

Exercise $\PageIndex{H}$

$\bigstar$ Find the exact value of each expression.

89. $\cos \dfrac{π}{6} \\[2pt]$ 90. $\sin \dfrac{π}{6}$

91. $\cot \dfrac{π}{6} \\[2pt]$ 92. $\tan \dfrac{π}{6}$

93. $\csc \dfrac{π}{4} \\[2pt]$ 94. $\sec \dfrac{π}{4}$

95. $\tan \dfrac{π}{4} \\[2pt]$ 96. $\cos \dfrac{π}{4}$

97. $\sec \dfrac{π}{3} \\[2pt]$ 98. $\csc \dfrac{π}{3}$

99. $\sin \dfrac{π}{3} \\[2pt]$ 100. $\cot \dfrac{π}{3}$

Answers to Odd Problems

89. $\frac{\sqrt{3}}{2}$ $\qquad$ 91. $\sqrt{3}$ $\qquad$ 93. $\sqrt{2}$ $\qquad$ 95. $1$ $\qquad$ 97. $2$ $\qquad$ 99. $\frac{\sqrt{3}}{2}$

$\bigstar$ Use reference angles to evaluate the expression.

101.  $\sec \dfrac{7π}{6}$ 102.  $\tan \dfrac{5π}{6}$

103.  $\cot \dfrac{13π}{6}$ 104.  $\csc \dfrac{11π}{6}$

105.  $\sec \dfrac{3π}{4}$ 106.  $\tan \dfrac{7π}{4}$

107.  $\cot \dfrac{19π}{4}$ 108.  $\csc \dfrac{11π}{4}$

109.  $\csc \dfrac{10π}{3}$ 110.  $\cot  \dfrac{10π}{3}$

111. $\tan  \dfrac{11π}{3}$ 112.  $\sec   \dfrac{5π}{3}$

113.  $\sec 300°$ 114.  $\tan 225°$

115.  $\cot 240°$ 116.  $\csc 150°$

117.  $\sec 120°$ 118.  $\tan 330°$

119.  $\cot 315°$ 120.  $\csc 210°$

$\bigstar$  For each of the following angles, find exact values for $\sec \left(\theta \right),\csc \left(\theta \right),\; \tan \left(\theta \right),\; \cot \left(\theta \right)\;$.

121.  $\theta =\dfrac{5\pi \; }{6}$

122.  $\theta =\dfrac{7\pi \; }{4}$

123.  $\theta =\dfrac{2\pi \; }{3}$

124.  $\theta =\dfrac{4\pi \; }{3}$

$\bigstar$  Evaluate the following expressions exactly.

125.  a. $\sec \left(135{}^\circ \right)$  b. $\csc \left(210{}^\circ \right)$  c. $\tan \left(60{}^\circ \right)$   d. $\cot \left(225{}^\circ \right)$

126. a. $\sec \left(30{}^\circ \right)$   b. $\csc \left(315{}^\circ \right)$  c. $\tan \left(135{}^\circ \right)$  d. $\cot \left(150{}^\circ \right)$

Answers to Odd Problems

101. $−\frac{2\sqrt{3}}{3}$ $\;\;$ 103. $\sqrt{3}$ $\;\;$ 105. $−\sqrt{2}$ $\;\;$ 107. $−1$ $\quad \;\; 109. -\dfrac{2\sqrt{3}}{3}$ $\;\;$ 111. $−\sqrt{3}$ $\;\;$ 113. $2$ $\;\;$ 115. $\frac{\sqrt{3}}{3}$ $\;\;$ 117. $−2$ $\;\;$ 119. $−1$.

121. $\text{sec} (\theta) = -\frac{2\sqrt{3}}{3}$, $\text{csc} (\theta) = 2$, $\text{tan} (\theta) = -\frac{\sqrt{3}}{3}$, $\text{cot} (\theta) = -\sqrt{3}$

123. $\text{sec} (\theta) = -2$, $\text{csc} (\theta) = \frac{2\sqrt{3}}{3}$, $\text{tan} (\theta) = -\sqrt{3}$, $\text{cot} (\theta) = -\frac{\sqrt{3}}{3}$

125. a. $\text{sec} (135^{\circ}) = -\sqrt{2}$ $\quad$ b. $\text{csc} (210^{\circ}) = -2$ $\quad$ c. $\text{tan} (60^{\circ}) = \sqrt{3}$ $\quad$ d. $\text{cot} (225^{\circ}) = 1$

I: Use a calculator

Exercise $\PageIndex{I}$

$\bigstar$  Use a calculator to evaluate to three decimal digits.

131.  $\cot \dfrac{4π}{7} \\[2pt]$ 132.  $\csc \dfrac{5π}{9}$

133.  $\tan \dfrac{5π}{8} \\[2pt]$ 134.  $\sec \dfrac{π}{10}$

135.  $\csc \dfrac{π}{4} \\[2pt]$ 136.  $\sec \dfrac{3π}{4}$

137.  $\cot 33° \\[6pt]$ 138.  $\tan 98°$

139.  $\sec 310° \\[6pt]$ 140.  $\cot 140°$

$\bigstar$  Use a calculator to find secant, cosecant, and cotangent of the following angles to four decimal digits:

141.  0.15 142.  0.5

143.  4 144.  5.2

145.  70$\mathrm{{}^\circ}$ 146.  10$\mathrm{{}^\circ}$

147.  283$\mathrm{{}^\circ}$ 148.  195$\mathrm{{}^\circ}$

Answers to Odd Problems

131. $–0.228$ $\qquad$ 133. $–2.414$ $\qquad$ 135. $1.414$ $\qquad$ 137. $1.540$ $\qquad$ 139. $1.556$

141. $\csc(0.15) = 6.6917$ $\qquad$ $\sec(0.15) = 1.0114$ $\qquad$ $\cot(0.15) = 6.6166$
143. $\csc(4) = -1.3213$    $\quad \;\;$ $\sec(4) = -1.5299$    $\quad \;\;$ $\cot(4) = 0.8637$
145. $\csc( 70^{\circ}) = 1.0642$    $\qquad$ $\sec(70^{\circ}) = 2.9238$   $\qquad$ $\cot(70^{\circ}) = 0.3640$
147. $\csc( 283^{\circ} ) = -1.0263$  $\quad \;\;$ $\sec( 283^{\circ} ) = 4.4454$  $\quad \;\;$ $\cot( 283^{\circ} ) = -0.2309$

J: Symmetry, Even/Odd Identities, Cofunction Identities

Exercise $\PageIndex{J}$

151. If $\sin (t)= \dfrac{\sqrt{2}}{2},$ what is the $\sin (−t)$? 152. If $\cos (t)= \dfrac{1}{2},$ what is the $\cos (−t)$?

153. If $\sec (t)=3.1,$ what is the $\sec (−t)$? 154. If $\csc (t)=0.34,$ what is the $\csc (−t)$? 155. If $\tan (t)=−1.4,$ what is the $\tan (−t)$? 156. If $\cot (t)=9.23,$ what is the $\cot (−t)$?

$\bigstar$  Determine whether the function is even, odd, or neither.

157. $f(x)=3 \sin ^2 x \cos x + \sec x$ 158. $f(x)=2 \sin x \cos x$

159. $f(x)= \csc ^2 x+ \sec x$ 160. $f(x)= \sin x −2 \cos ^2 x$

Answers to Odd Problems

151. $−\frac{\sqrt{2}}{2}$ $\qquad$ 153. $3.1$ $\qquad$ 155. $1.4$ $\qquad$ 157. even $\qquad$ 159. even $\qquad$.

$\bigstar$  Use cofunctions of complementary angles.

161.   $\cos \left(\dfrac{2π}{7} \right)= \_\_\_ (\_\_\_)$

162.   $\sin (76°)= \_\_\_ (\_\_°)$

163.  $\csc (38°) = \_\_\_ (\_\_\_°)$

164.  $\tan \left(\dfrac{3π}{5}\right)= \_\_\_ (\_\_)$

$\bigstar$  Use reciprocal, quotient, and Pythagorean Identities to determine the following.

171. Given $\sin \theta = 0.4$,  find     (a) $\cos \theta$     (b) $\tan\theta$     (c) $\csc \theta$

172. Given $\cos \theta = 0.7$, find     (a) $\sin \theta$     (b) $\sec \theta$     (c) $\cot \theta$

173. Given $\tan \theta = 2$,   find     (a) $\cot \theta$     (b) $\sec \theta$     (c) $\cos \theta$

174. Given $\csc \theta = 3$,   find     (a) $\sin \theta$     (b) $\cot \theta$     (c) $\tan \theta$

175. Given $\sec \theta = 4$,   find     (a) $\cos \theta$     (b) $\sin \theta$     (c) $\tan \theta$

176. Given $\cot \theta = 5$,   find     (a) $\tan \theta$     (b) $\csc \theta$     (c) $\sec \theta$

Answers to Odd Problems

161. $\sin \dfrac{3π}{14}$     163.  $\sec (52°)$.      171. (a) $\pm \: .2\sqrt{21} \approx \pm \: 0.9165,$  (b) $\pm \frac{2}{\sqrt{21}} \approx \pm \: .4364$, (c) $2.5$
173. (a) $0.5,$  (b) $\pm \sqrt{5} \approx \pm \: 2.236$, (c) $\pm \frac{\sqrt{5}}{5} \approx \pm \: .447$     175. (a) $0.25,$  (b) $\pm \frac{\sqrt{15}}{4} \approx \pm \: .968$, (c) $\pm \sqrt{15} \approx \pm \: 3.873$

$\star$