6.2: Trigonometric Equations

Linear Trigonometric Equations

In Section 5.5, we determined the height of a rider on the London Eye Ferris wheel could be determined by the equation

\(h(t)=-65\cos \left(\dfrac{\pi }{15} t\right)+70. \)

If we wanted to know the length of time during which the rider is more than 100 meters above ground, we would need to solve equations involving trigonometric functions.

Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Although similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval. However, just as often, we will be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. Additionally, like rational equations, the domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is \(2\pi\). In other words, every \(2\pi\) units, the y-values repeat. If we need to find all possible solutions, then we must add \(2\pi k\), where \(k\) is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is \(2\pi\):

\[\sin \theta=\sin(\theta \pm 2k\pi) \nonumber \]

There are similar rules for indicating all possible solutions for the other trigonometric functions.

 How to: Solve Linear Trigonometric Equations having a Simple Argument

1. Isolate the trigonometric function (sine, cosine, or tangent) on one side of the equation. The final result for this step should look like \(\sin (x) = y\) or \(\cos (x) = y\) or \(\tan (x) = y\), where \(y\) is a real number or real number expression. If the function is not sine, cosine, or tangent, use a Reciprocal Identity to change it:

\(\sec (t)=\dfrac{1}{\cos (t)}\quad \quad \csc (t)=\dfrac{1}{\sin (t)}\quad \quad \cot (t)=\dfrac{1}{\tan (t)}\)

2. Use inverse trigonometric functions to find one solution
3. Find a second solution on one cycle, when a second solution exists.  Sine and cosine have 2 solutions per cycle (except when the sine or cosine ratio is 1 or -1) because the period of one cycle is \(P=2\pi\) and they oscillate between \(1\) and \(-1\) and back again. A tangent function just has one solution, because the period \(P=\pi\) for tangent is half the length of that for sine or cosine, and the graph only increases or only decreases within that cycle.
4. Find additional solutions if needed, by writing a general solution that involves multiples of the period (use \(k\) to represent any integer). Given a solution \(s\), these general solutions look like

\(x = s + 2\pi k \) for sine or cosine \( \qquad \) or \( \qquad \) \(x = s + \pi k\) for tangent

Solutions that are Special Angles

Simple Arguments

In the last chapter, we learned sine and cosine values at commonly encountered ("special") angles. We can use these to solve sine and cosine equations involving these common angles.

Often the question will ask just for solutions in a given interval.

Example \(\PageIndex{1}\)

A circle of radius \(5\sqrt{2}\) intersects the line \(x = -5\) at two points. Find the angles \(\theta\) on the interval \(0 \le \theta <2\pi\), where the circle and line intersect.

Solution

T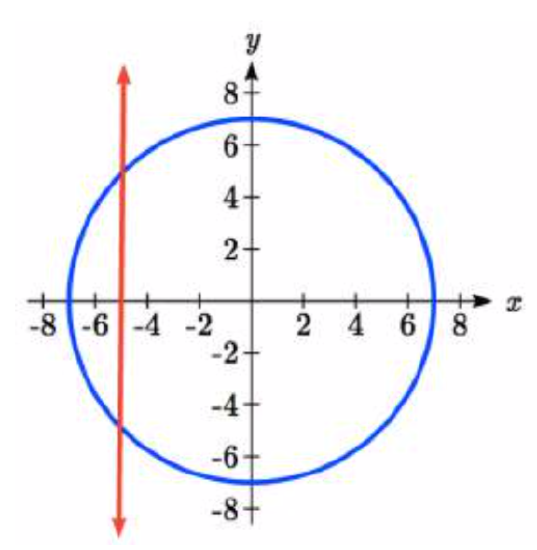he \(x\) coordinate of a point on a circle can be found as \(x=r\cos \left(\theta \right)\), so the \(x\) coordinate of points on this circle would be \(x=5\sqrt{2} \cos \left(\theta \right)\). To find where the line \(x = -5\) intersects the circle, we can solve for where the \(x\) value on the circle would be \(-5\).

\(\begin{array} {rcll}
5\sqrt{2} \cos \left(\theta \right)   &=&-5 &\text{Isolate the cosine}\\[2pt]
\cos \left(\theta \right)  &=& \dfrac{-5}{5\sqrt{2}} = \dfrac{-1}{\sqrt{2} } = \dfrac{-1}{\sqrt{2} } \cdot \dfrac{\sqrt{2}}{\sqrt{2}}  \\[2pt]
\cos \left(\theta \right)  &=&  -\dfrac{\sqrt{2}}{2}\\
\end{array}\)

We recognize this as one of our special cosine values. The reference angle is \(\dfrac{\pi}{4}\) because \(\cos \dfrac{\pi}{4} = \dfrac{\sqrt{2} }{2}\), but the desired angles are in Quadrants II and III where the cosine function is negative, as the unit circle diagram suggests. Our solutions are angles

\[\theta =\dfrac{3\pi }{4}\text{ and }\theta =\dfrac{5\pi }{4}\nonumber\]

Example \(\PageIndex{2}\): Solve a Linear Equation Involving Cosine

Solve the equation exactly: \(2 \cos \theta−3=−5\), \(0≤\theta<2\pi\).

Solution

Use algebraic techniques to solve the equation.

\[\begin{align*} 2 \cos \theta-3&= -5\\ 2 \cos \theta&= -2\\ \cos \theta&= -1\\ \theta&= \pi \end{align*}\]

Other times, an expression that gives all possible solutions is desired. Two of the solutions are unique; all the others are coterminal with those two solutions. 

Example \(\PageIndex{3}\): Find the General Solution to a Linear Equation Involving Sine

Solve \(\sin \left(t\right)=\dfrac{1}{2}\) for all possible values of \(t\).

Solution

Notice this is asking us to identify all angles, \(t\), that have a sine value of \(\dfrac{1}{2}\). While evaluating a function always produces one result, solving for an input can yield multiple solutions. Two solutions should immediately jump to mind from the last chapter: \(t=\dfrac{\pi }{6}\) and \(t=\dfrac{5\pi }{6}\) because they have the same reference angle and are in quadrants where \(y\) (and thus the sine function) are positive, and because they are the common angles on the unit circle with a sin of \(\dfrac{1}{2}\).

Looking at a graph confirms that there are more than these two solutions. While eight are seen on this graph, there are an infinite number of solutions!

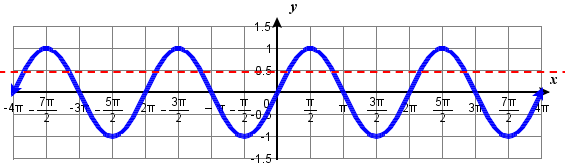
Remember that any coterminal angle will also have the same sine value, so any angle coterminal with these our first two solutions is also a solution. Coterminal angles can be found by adding or subtracting full rotations of 2\(\pi \), so we can write the full set of solutions:

\(t=\dfrac{\pi }{6} +2\pi k\) where k is any integer, and \(t=\dfrac{5\pi }{6} +2\pi k\) where \(k\) is any integer.

Example \(\PageIndex{4}\): Find the General Solution to a Linear Equation Involving Cosine 

Find all possible exact solutions for the equation \(\cos \theta=\dfrac{1}{2}\).

Solution

The cosine ratio is positive, so one of the angles is in Quadrant I. We know \( \cos \dfrac{\pi}{3} = \dfrac{1}{2},\) so therefore one of the solutions is \( \dfrac{\pi}{3}\). The other solution is in Quadrant IV, with the same reference angle. Thus the other solution is \(\dfrac{5\pi}{3}\). The same result could be obtained from analysis using the unit circle

These are the solutions in the interval \([ 0,2\pi ]\). All possible solutions are given by

\[\theta=\dfrac{\pi}{3} + 2k\pi \quad \text{and} \quad \theta=\dfrac{5\pi}{3} + 2k\pi \nonumber\]

where \(k\) is any integer.

When we are given equations that involve only one of the six trigonometric functions, their solutions involve using algebraic techniques and solving inverse trigonometric equations. We need to make several considerations when the equation involves trigonometric functions other than sine and cosine. Problems that involve reciprocals of the primary trigonometric functions must first be rewritten in terms of the primary function and then solved.

Example \(\PageIndex{5}\): Solve a Linear Equation Involving Cosecant

Solve the following equation exactly: \(\csc \theta=−2\), \(0≤\theta<4\pi\).

Solution

We want all values of \(\theta\) for which \(\csc \theta=−2\) over the interval \(0≤\theta<4\pi\).

\[\begin{align*} \csc \theta&= -2 &&\text{Rewrite as the reciprocal function}\\ \dfrac{1}{\sin \theta}&= -2\\ \sin \theta&= -\dfrac{1}{2} &&\text{The reference angle is \(\dfrac{\pi}{6}\) and solutions are in QIII and QIV}\\ \theta &= \dfrac{7\pi}{6},\space \dfrac{11\pi}{6} &&\text{Solutions in one cycle} \end{align*}\]

Because we are told to find solutions up to \(4\pi\), we must find other solutions that are coterminal to these. This is done by adding \(2\pi\) to each of these answers. Our final result is \(\boxed{\dfrac{7\pi}{6},\space \dfrac{11\pi}{6} ,\space \dfrac{19\pi}{6}, \space \dfrac{23\pi}{6}  } \).

An equation involving the tangent function is slightly different from one containing a sine or cosine function. First, as we know, the period of tangent is \(\pi\), not \(2\pi\). Further, the domain of tangent is all real numbers with the exception of odd integer multiples of \(\dfrac{\pi}{2}\), unless, of course, a problem places its own restrictions on the domain. 

Example \(\PageIndex{6}\): Find the General Solution to a Linear Equation Involving Tangent

Identify all exact solutions to the equation \(2(\tan x+3)=5+\tan x\), \(0≤x<2\pi\).

Solution

Isolate the expression \(\tan x\) on the left side of the equals sign. \(\qquad 2 \tan x+6=5+\tan x \rightarrow \tan x = -1.\)

From \(\tan \dfrac{\pi}{4} = 1\) we know the reference angle for the solutions is \( \dfrac{\pi}{4}\).  Because the tangent ratio (\(-1\)) is negative, the solution angles have the same reference angle but are in quadrants QII and QIV.

Therefore the two angles (which could also be derived from using the unit circle) are: \(\qquad x=\dfrac{3\pi}{4}\) and \(x=\dfrac{7\pi}{4}\).

Try It  \(\PageIndex{7}\)

Solve

1. \(2 \sin x+1=0\) for all exact solutions on the interval \([0,2\pi)\).
2. \(\sec x=-2\) for all possible values of \(x\).
3. \(\tan \left(t\right)=1\) for all possible values of \(t\).

Answer

a. \(x=\dfrac{7\pi}{6},\space \dfrac{11\pi}{6}\)

b.  \(x=\dfrac{2\pi}{3} + 2 \pi k,   \space \dfrac{4\pi}{3}+ 2 \pi k \)

c. From our special angles, we know one answer is \(t=\dfrac{\pi }{4}\). Recall that one cycle for the tangent function is \(\pi\), not \(2\pi\) like for sine and cosine. Tangent equations only have one unique solution per cycle or period, so additional solutions can be found by adding multiples of a full period, \(\pi \). \[t=\dfrac{\pi }{4} +\pi k\nonumber\]

Arguments that are Expressions 

When the argument is an expression, rather than just a simple variable, a substitution approach is helpful.

 How to: Solve Linear Trigonometric Equations having an Argument that is an Expression

1. Rewrite the equation so it just contains one trigonometric function - sine, cosine, or tangent. Isolate the trigonometric function on one side of the equation. 
2. If the argument is an expression, substitute the expression with the variable \(u\).
3. Use inverse trigonometric functions to find one solution for \(u\).
4. Find a second solution for \(u\) on one cycle, when a second solution exists.  Sine and cosine have 2 solutions (or one if the ratio is \(\pm1\)); tangent just has one solution.
5. Find additional solutions for \(u\) if needed by writing a general solution that involves multiples of the period ( use \(k\) to represent any integer).
6. Undo the substitution, if one was made in step 2. Replace \(u\) in the solution formula with the expression that was replaced with \(u\) in step 2, and then solve for the original variable.

Example \(\PageIndex{8}\): Solving a Multiple Angle Trigonometric Equation

Solve exactly: \(\cos(2x)=\dfrac{1}{2}\) on \([ 0,2\pi )\).

Solution

We can see that this equation is the standard equation with a multiple of an angle. (Replace the argument expression, \(2x\), with \(u\) and find solutions for \(u\) in one cycle of the cosine function.

\(\begin{array} {rcl}
\cos(u)=\dfrac{1}{2}  & \text{Substitution made: \( \color{Cerulean}{u=2x} \) }  \\[2pt]
u &=    \cos^{-1} \left( \dfrac{1}{2} \right)     & \text{Solutions in QI and QIV with ref. angle \( \dfrac{\pi}{3}\)} \\[2pt]
u =    \dfrac{\pi}{3} &\text{   and    } u =    \dfrac{5\pi}{3}
\end{array}\)

We saw the solutions to this equation were

\(\begin{array} {c|cl}
u =\dfrac{\pi }{3}   & u=\dfrac{5\pi }{3}  \\[2pt]
u =\dfrac{\pi }{3} +2\pi k   &     u=\dfrac{5\pi }{3} +2\pi k &\text{General solutions, where \(k\) is any integer}\\[2pt]
2x =\dfrac{\pi }{3} +2\pi k   &    2x=\dfrac{5\pi }{3} +2\pi k &\text{Replace the \(u\) in the solutions with \(2x \) }\\[2pt]
 x =\dfrac{\pi }{6} +\pi k     &   x =\dfrac{5\pi }{6} +\pi k  &\text{Solve for \(x\).  }\\[6pt]
x =\dfrac{\pi }{6}   &    x =\dfrac{5\pi }{6}      & \qquad \text{solutions when \(k=0\)}\\
x =\dfrac{7\pi }{6}   &    x =\dfrac{11\pi }{6}      &\qquad \text{solutions when \(k=1\) }\\
x =\dfrac{13\pi }{6}   &    x =\dfrac{17\pi }{6}      &\qquad k = 2 \text{ solutions are too big!}\\
\end{array}\)

Our solutions are \(x=\dfrac{\pi}{6}, \space \dfrac{5\pi}{6}, \space \dfrac{7\pi}{6}\), and \(\dfrac{11\pi}{6}\). Note that whenever we solve a problem in the form of \( \sin (nx) =c\), we will get \(n\) times as many solutions as exist in one cycle of the function.

Example  \(\PageIndex{9}\): Multiple Angle Application

The depth of water at a dock rises and falls with the tide, following the equation \(f(t)=4\sin \left(\dfrac{\pi }{12} t\right)+7\), where t is measured in hours after midnight. A boat requires a depth of 9 feet to tie up at the dock. Between what times will the depth be 9 feet or more?

Solution

To find when the depth is 9 feet, we need to solve \(f(t) = 9\).

\(\begin{array} {rcl}
4\sin \left(\dfrac{\pi }{12} t\right)+7&=9 & \text{Isolate the sine} \\[2pt]
4\sin \left(\dfrac{\pi }{12} t\right)&=2& \text{Divide by \(4\)} \\[2pt]
\sin \left(\dfrac{\pi }{12} t\right)&=\dfrac{1}{2}
\end{array}\)

Define  a new temporary variable \(u\) to be \(\color{Cerulean}{u=\dfrac{\pi }{12} t}\), so our equation \(\sin \left(\dfrac{\pi }{12} t\right)=\dfrac{1}{2}\) becomes 

\(\sin \left(u\right)=\dfrac{1}{2}\).

\(\begin{array} {c|cl}
u =\dfrac{\pi }{6}    & u=\dfrac{5\pi }{6}  \\[2pt]
u =\dfrac{\pi }{6} +2\pi k   & u=\dfrac{5\pi }{6} +2\pi k &\text{General solutions}\\[2pt]
\dfrac{\pi }{12} t =\dfrac{\pi }{6} +2\pi k   & \dfrac{\pi }{12} t=\dfrac{5\pi }{6} +2\pi k &\text{"Undo" sub - replace \(u\) }\\[2pt]
 t =\dfrac{\dfrac{\pi }{6}}{\dfrac{\pi }{12}} +\dfrac{2\pi k}{\dfrac{\pi }{12}} & t =\dfrac{\dfrac{5\pi }{6}}{\dfrac{\pi }{12}} +\dfrac{2\pi k}{\dfrac{\pi }{12}}  &\text{Solve for \(t\).  }\\[2pt]
t=2+24k  & t=10+24k\\
\end{array}\)

The depth will be 9 feet and the boat will be able to approach the dock between 2 am and 10 am.

Notice how in both scenarios, the 24k shows how every 24 hours the cycle will be repeated.

In the previous example, looking back at the original simplified equation \(\sin \left(\dfrac{\pi }{12} t\right)=\dfrac{1}{2}\), we can use the ratio of the “normal period” to the stretch factor to find the period: \(\dfrac{2\pi }{\left(\dfrac{\pi }{12} \right)} =2\pi \left(\dfrac{12}{\pi } \right)=24\). Notice that the sine function has a period of 24, which is reflected in the solutions: there were two unique solutions on one full cycle of the sine function, and additional solutions were found by adding multiples of a full period.

Example \(\PageIndex{10}\): Multiple Angle Equation Involving Tangent

Solve the equation exactly: \(\tan\left(\theta−\dfrac{\pi}{2}\right)=1\), \(0≤\theta<2\pi\).

Solution

The initial substitution is \(u=\theta−\dfrac{\pi}{2}\). Solving the equation \(\tan u = 1\) produces one solution, \(u= \dfrac{\pi}{4}\) .

Recall that the tangent function has a period of \(\pi\). So there is only one solution in one cycle of the tangent function. All others can be obtained from the general form of the solution set, \(u= \dfrac{\pi}{4} + \pi k\), where \(k\) is any integer.

Now we need to solve for our original variable, \(\theta\):    \(\theta−\dfrac{\pi}{2}= \dfrac{\pi}{4} + \pi k\ \rightarrow \theta=\dfrac{3\pi}{4} + \pi k \)

When \(k=0\) we obtain the solution \( \theta=\dfrac{3\pi}{4}\). When \(k=1\) we get \(\theta=\dfrac{7\pi}{4}\). When \(k=2\) the answer we get is \(\dfrac{11\pi}{4}\), which is larger than \(2\pi\), so it must be rejected for this problem.

Over the interval \([ 0,2\pi )\), we have two solutions: \(\theta=\dfrac{3\pi}{4}\) and \(\theta=\dfrac{7\pi}{4}\)

 Try It  \(\PageIndex{11}\)

Solve \(4\sin (5t)-1=1\) for all possible values of \(t\).

Answer

\(\begin{array} {cl|}
  4\sin (5t)-1=1  &  \text{Isolate the cosine}  \\[2pt]
      \sin (5t)=\dfrac{1}{2} &  \text{Let \(u=5t\)} \\[2pt]
      \sin (u)=\dfrac{1}{2}         \\[2pt]
\end{array}\) \(\begin{array} {ccl}
u=\dfrac{\pi }{6} +2\pi k  & u=\dfrac{5\pi }{6} +2\pi k   &\text{General solutions}\\[2pt]
5t=\dfrac{\pi }{6} +2\pi k  &   5t = \dfrac{5\pi }{6} +2\pi k  &\text{Solve for \(t\)}   \\[2pt]
t=\dfrac{\pi }{30} +\dfrac{2\pi }{5} k  &  t=\dfrac{\pi }{6} +\dfrac{2\pi }{5} k
\end{array}\)

Solutions that Require a Calculator

Not all equations involve the “special” values of the trigonometric functions to we have learned. To find solutions to these kind of equations, we need to use an inverse trig function operation on a calculator.

Simple Arguments that need a calculator

Example \(\PageIndex{12}\)

Use the inverse sine function to find one solution to \(\sin \left(\theta \right)=0.8\).

Solution

Since this is not a known value, a calculator must be used to find the angle \(\theta =\sin ^{-1} \left(0.8\right)\). The result is an approximate value for this angle. If your calculator is in degree mode, your calculator will give you an angle in degrees as the output. If your calculator is in radian mode, your calculator will give you an angle in radians. In radians, \(\theta =\sin ^{-1} \left(0.8\right)\approx 0.927\), or in degrees, \(\theta =\sin ^{-1} \left(0.8\right)\approx 53.130{}^\circ\).

Always make sure you are using the appropriate mode on your calculator -- degrees or radians. In calculus, we will almost always want to work with radians since they are unit-less.

Notice that the inverse trigonometric functions do exactly what you would expect of any function – for each input they give exactly one output. While this is necessary for these to be a function, it means that to find all the solutions to an equation like \(\sin \left(\theta \right)=0.8\), we need to do more than just evaluate the inverse function.

To find additional solutions, it is good to remember four things:

• The sine is the \(y\)-value of a point on the unit circle
• The cosine is the \(x\)-value of a point on the unit circle
• The tangent is the slope of a line at a given angle
• Other angles with the same \(\sin\)/\(\cos\)/\(\tan\) will have the same reference angle

Example \(\PageIndex{13}\): Find all solutions

Find all solutions to \(\sin \left(\theta \right)=0.8\).

Solution

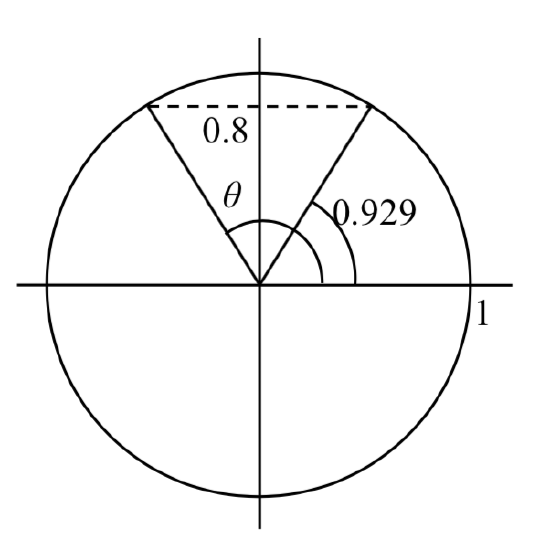We would expect two unique angles on one cycle to have this sine value. In the previous example, we found one solution to be \(\theta =\sin ^{-1} \left(0.8\right)\approx 0.927\). To find the other, we need to answer the question “what other angle has the same sine value as an angle of 0.927?”

We can think of this as finding all the angles where the y-value on the unit circle is 0.8. Drawing a picture of the circle helps to show in which quadrant another angle with the same \(y\) coordinate would be positioned.

The second angle would have the same reference angle and reside in the second quadrant (where \(y\) coordinates are also positive). This second angle would be located at \(\theta =\pi -\sin ^{-1} (0.8)\), or approximately \(\theta \approx \pi -0.927=2.214\).

To find more solutions we recall that angles coterminal with these two would have the same sine value, so we can add full cycles of 2\(\pi \).

\(\begin{array} {rcll}
\theta =\sin ^{-1} (0.8) +2\pi k  &\text{ and } & \theta =\pi -\sin ^{-1} (0.8)+2\pi k \\[2pt]
\theta =0.927+ +2\pi k  &\text{ and } & \theta =2.214+2\pi k \\[2pt]
\end{array}\)
Approximate solutions, where \(k\) is an integer.

Example \(\PageIndex{14}\) 

Find all solutions to \(\sin \left(x\right)=-\dfrac{8}{9}\) on the interval \(0{}^\circ \le x<360{}^\circ\).

Solution

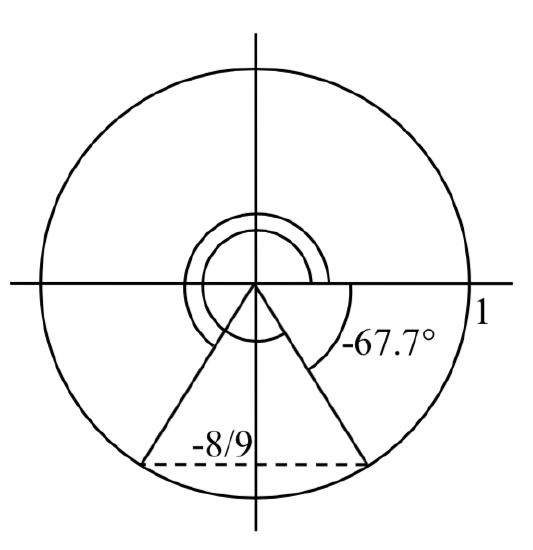We are looking for the angles with a \(y\)-value of -8/9 on the unit circle. Immediately we can see the solutions will be in the third and fourth quadrants (where the \(y\) coordinates are negative).

First, we will turn our calculator to degree mode. Using the inverse, we can find one solution \(x=\sin ^{-1} \left(-\dfrac{8}{9} \right)\approx -62.734{}^\circ\). While this angle satisfies the equation, it does not lie in the domain we are looking for. To find the angles in the desired domain, we start looking for additional solutions.

First, an angle coterminal with \(-62.734{}^\circ\) will have the same sine. By adding a full rotation, we can find an angle in the desired domain with the same sine.

\(x=-62.734{}^\circ +360{}^\circ =297.266{}^\circ\)

There is a second angle in the desired domain that lies in the third quadrant. Notice that \(62.734{}^\circ\) is the reference angle for all solutions, so this second solution would be \(62.734{}^\circ\) past \(180{}^\circ\)

\(x=62.734{}^\circ +180{}^\circ =242.734{}^\circ\)

The two solutions on \(0{}^\circ \le x<360{}^\circ\) are \(x\) = \(297.266{}^\circ\) and \(x\) = \(242.734{}^\circ\)

Example \(\PageIndex{15}\)

Find all solutions to \(\tan \left(x\right)=3\) on \(0 \le x<2\pi\).

Solution

Using the inverse tangent function, we can find one solution \(x=\tan ^{-1} \left(3\right) \approx 1.249\). Unlike the sine and cosine, the tangent function only attains any output value once per cycle, so there is no second solution in any one cycle.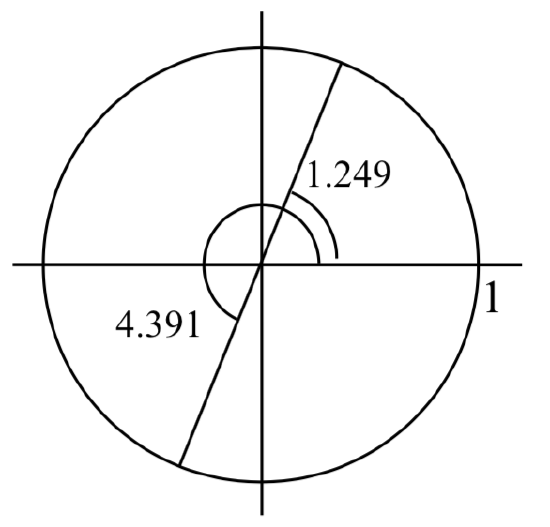

By adding \(\pi \), a full period of tangent function, we can find a second angle with the same tangent value. Notice this gives another angle where the line (along the terminal side of the angle) has the same slope.

If additional solutions were desired, we could continue to add multiples of \(\pi \), so all solutions would take on the form \(x=1.249+k\pi\), however we are only interested in \(0 \le x< 2\pi\).

\(x=1.249+\pi =4.391\)

The two solutions on \(0\le x<2\pi\) are \(x = 1.249\) and \(x = 4.391\).

 Try It  \(\PageIndex{16}\)

Find all solutions to \(\tan \left(x\right)=0.7\) on \(0{}^\circ \le x<360{}^\circ\).

Answer

The first solution is \(x=\tan ^{-1} (0.7) \approx 34.992{}^\circ\).

For a standard tangent, the second solution can be found by adding a full period, \(180\mathrm{{}^\circ}\), giving \[x=180{}^\circ +34.99{}^\circ =214.992{}^\circ\nonumber\]

Example \(\PageIndex{17}\)

Solve \(3\cos \left(t\right)+4=2\) for all solutions on one cycle, \(0\le t<2\pi\)

Solution

\(\begin{array} {rll}
3\cos \left(t\right)+4  &=2   &\text{Isolate the cosine}\\[2pt]
3\cos \left(t\right)  &=-2    \\[2pt]
\cos \left(t\right)  &=-\dfrac{2}{3}   &\text{Use the inverse, to find one solution}\\[2pt]
t  &=\cos ^{-1} \left(-\dfrac{2}{3} \right)   \\[2pt]
t  &\approx 2.301 
\end{array}\)

We’re looking for two angles where the \(x\)-coordinate on a unit circle is -2/3. A second angle with the same cosine would be located in the third quadrant. Notice that the location of this angle could be represented as \(t=-2.301\). To represent this as a positive angle we could find a coterminal angle by adding a full rotation.

\[t=-2.301+2\pi = 3.982\nonumber\]

The equation has two solutions between 0 and 2\(\pi \), at \(t = 2.301\) and \(t = 3.982\).

Example \(\PageIndex{18}\): Using a Calculator to Solve a Trigonometric Equation Involving Secant

Use a calculator to solve the equation \( \sec θ=−4, \) giving your answer in radians.

Solution

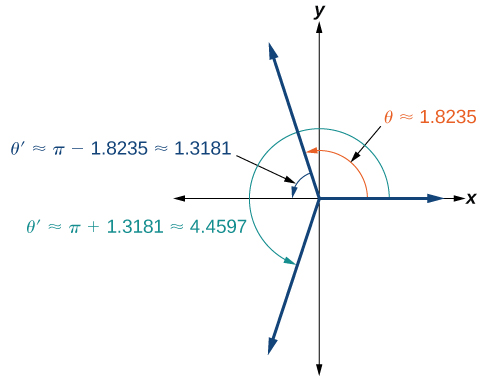We can begin with some algebra.

\[\begin{align*} \sec \theta&= -4\\ \dfrac{1}{\cos \theta}&= -4\\ \cos \theta&= -\dfrac{1}{4} \end{align*}\]

Check that the MODE is in radians. Now use the inverse cosine function

\(\begin{align*}{\cos}^{-1}\left(-\dfrac{1}{4}\right) \approx 1.8235\\ \theta \approx 1.8235+2\pi k \end{align*}\)

Since \(\dfrac{\pi}{2}≈1.57\) and \(\pi≈3.14\), and we know \(1.8235\) is between these two numbers, so\(\theta≈1.8235\) is in quadrant II. Cosine is also negative in quadrant III. Note that a calculator will only return an angle in quadrants I or II for the inverse cosine function, since that is the range of the inverse cosine. See the Figure on the right.

So, we also need to find the measure of the angle in quadrant III. In quadrant III, the reference angle is \( \alpha ≈\pi−1.8235≈1.3181\). The other solution in quadrant III is \(\pi + \alpha ≈\pi+1.3181≈4.4597\).

The solutions are \(\theta≈1.8235 + 2\pi k\) and \(\theta≈4.4597 + 2\pi k\).

 Try It \(\PageIndex{19}\)

Solve \(\cos \theta=−0.2\).

Answer

\(\theta≈1.7722 + 2\pi k\) and \(\theta≈4.5110 + 2\pi k\)

Arguments that are Expressions that need a calculator

Example \(\PageIndex{20}\)

Solve \(\cos \left(3t\right)=0.2\) for all solutions on two cycles, \(0\le t<\dfrac{4\pi }{3}\).

Solution

As before, with a horizontal compression it can be helpful to make a substitution, \(u=3t\) Making this substitution simplifies the equation to a form we have already solved.

\(\begin{array} {c} \cos \left(u\right)  =0.2   \\[2pt]
 u   =\cos ^{-1} \left(0.2\right)\approx 1.369 \end{array}\)

A second solution on one cycle would be located in the fourth quadrant with the same reference angle.

\[u\approx 2\pi -1.369=4.914\nonumber\]

In this case, we need all solutions on two cycles, so we need to find the solutions on the second cycle. We can do this by adding a full rotation to the previous two solutions.

\(\begin{array} {r|ll}
u = 1.369+2\pi k    &    u=4.914+2\pi  k    &\text{General solutions, \(k\) is any integer} \\[2pt]
3t = 7.653+2\pi k   &    3t=11.197+2\pi k  &\text{Replace \(u\)  with \(3t\)   }  \\[4pt]
t = 0.456 +\dfrac{2\pi}{3}k   &    t=1.638+\dfrac{2\pi}{3}k   &\text{General solutions for \(t\)}    \\[2pt]
t = \color{Cerulean}{0.456}    &    t=\color{Cerulean}{1.638} &\text{Solutions obtained when \(k=0\) } \\[2pt]
t = 0.456... +\dfrac{2\pi}{3}   &    t=1.638....+\dfrac{2\pi}{3}  &\text{Solutions obtained when \(k=1\) } \\[2pt]
t = \color{Cerulean}{2.551}   &    t=\color{Cerulean}{3.732}   \\[2pt]
\end{array}\)

The question asks for all solutions less than \(\dfrac{4\pi }{3} \approx 4.189 \), so the Solution Set is \( \{  0.456,\;\; 1.638, \;\;  2.551, \;\;  3.732  \} \).

Example \(\PageIndex{21}\)

Solve \(3\sin \left(\pi \, t\right)=-2\) for all solutions.

Solution

\(\begin{array} {rlll}
3\sin \left(\pi \, t\right)  &=-2    &\text{Isolate the sine} \\[2pt]
\sin \left(\pi \, t\right)   &=-\dfrac{2}{3}    &\text{Make the substitution \(u=\pi \, t\)} \\[2pt]
\sin \left(u\right)          &=-\dfrac{2}{3}    &\text{Use the inverse} \\[2pt]
u  &=\sin ^{-1} \left(-\dfrac{2}{3} \right)&\text{Find one solution} \\[2pt]
u  & \approx -0.730 
\end{array}\)

This angle is in the fourth quadrant. A second angle with the same (negative) sine ratio would be in the third quadrant with 0.730 as a reference angle: \(u=\pi +0.730=3.871\). We can write all solutions to the equation \(\sin \left(u\right)=-\dfrac{2}{3}\) as

\(\begin{array} {r|ll}
u = -0.730+2\pi k    &    u=3.871+2\pi k    &\text{General solutions, \(k\) is any integer} \\[2pt]
\pi t=-0.730+2\pi k   &    \pi t=3.871+2\pi k  &\text{Replace \(u\)  with \(\pi \, t\)   }  \\[2pt]
t=-0.232+2 k   &    t=1.232+2 k  &\text{Divide by \(\pi \) to get all (approximate) solutions}  \\[2pt]
\end{array}\)

The solutions are \( t=-0.232+2 k \) and \(t=1.232+2 k \), where \(k\) represents any integer.

 Try It  \(\PageIndex{22}\)

Solve \(5\sin \left(\dfrac{\pi }{2} t\right)+3=0\) for all solutions on one cycle, \(0 \le t < 4\).

Answer

\[\sin \left(\dfrac{\pi }{2} t\right)=-\dfrac{3}{5}\nonumber\]Let \(u=\dfrac{\pi }{2} t\), so this becomes \[\sin \left(u\right)=-\dfrac{3}{5}\nonumber\]

Using the inverse, \(u=\sin ^{-1} \left(-\dfrac{3}{5} \right)\approx -0.6435\). Since we want positive solutions, we can find the coterminal solution by adding a full rotation: \(u=-0.6435+2\pi =5.6397\). Another angle with the same sin would be in the third quadrant with the reference angle 0.6435. \(u=\pi +0.6435=3.7851\).

\(\begin{array} {c|cl}
u = 5.6397    &    u= 3.7851    &\text{Solutions for \(u\)} \\[2pt]
\dfrac{\pi }{2} t= 5.6397   &   \dfrac{\pi }{2} t=3.7851    &\text{Replace \(u\)  with \(\dfrac{\pi }{2} t\)   } \\[2pt]
 t=5.6397\left(\dfrac{2}{\pi } \right)   &    t=3.7851\left(\dfrac{2}{\pi } \right) &\text{Solve for \(t\)   }  \\[2pt]
t= 2.4097 &    t = 3.5903 
\end{array}\)

The solutions on one cycle are \(t= 2.4097 \) and \( t = 3.5903\).

Applications

We now can return to the question we began the section with.

Example \(\PageIndex{23}\)

The height of a rider on the London Eye Ferris wheel can be determined by the equation \(h(t)=-65\cos \left(\dfrac{\pi }{15} t\right)+70\). How long is the rider more than 100 meters above ground?

Solution

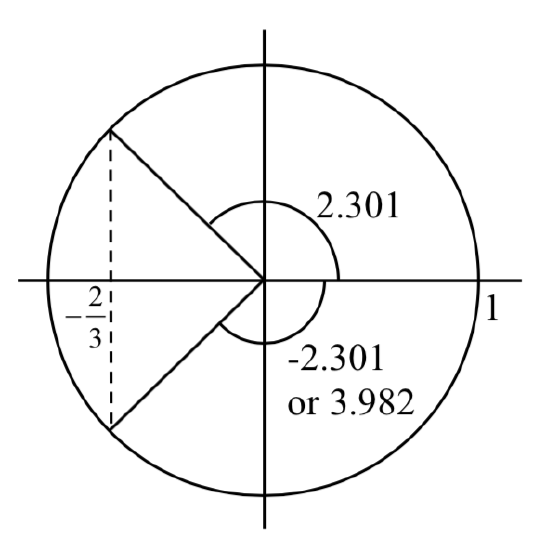To find how long the rider is above 100 meters, we first find the times at which the rider is at a height of 100 meters by solving h(t) = 100.

\(\begin{array} {rlll}
-65\cos \left(\dfrac{\pi }{15} t\right)+70  &=100    &\text{Isolate the cosine} \\[2pt]
-65\cos \left(\dfrac{\pi }{15} t\right)     &=30     \\[2pt]
\cos \left(\dfrac{\pi }{15} t\right)  &=\dfrac{30}{-65}    &\text{Make the substitution \(u=\dfrac{\pi }{15} t\)  } \\[2pt]
\cos (u)   &=  \dfrac{30}{-65}    &\text{Use the inverse} \\[2pt]
u  &=\cos ^{-1} \left(\dfrac{30}{-65} \right)   &\text{Find one solution} \\[2pt]
u  & \approx 2.051 
\end{array}\)

This angle is in the second quadrant. A second angle with the same cosine would be symmetric in the third quadrant. This angle could be represented as u = -2.051, but we need a coterminal positive angle, so we add 2\(\pi \): \(u=2\pi -2.051\approx 4.230\).

Now we can undo the substitution to solve for \(t\)

 

\(\begin{array} {rcll}
u = 2.051    &\text{ and }&   u=4.230    &\text{Solutions for \(u\)} \\[2pt]
\dfrac{\pi }{15} t=2.051   &\text{ and }&  \dfrac{\pi }{15} t=4.230    &\text{Replace \(u\)  with \(\dfrac{\pi }{15}\)   } \\[2pt]
t = \dfrac{2.051}{\dfrac{\pi }{15}}     &\text{ and }&    t=\dfrac{4.230}{\dfrac{\pi }{15}}      &\text{Solve for \(t\)   }  \\[2pt]
t = 9.793 &\text{ and } & t = 20.197
\end{array}\)

A rider will be at 100 meters after 9.793 minutes, and again after 20.197 minutes. From the behavior of the height graph, we know the rider will be above 100 meters between these times. A rider will be above 100 meters for 20.197 - 9.793 = 10.404 minutes of the ride.

Quadratic Trigonometric Equations

At the beginning of this section, we solved linear trigonometric equations. In this section, we explore the techniques needed to solve trigonometric equations that are quadratic in form. Techniques used to solve quadratic trigonometric equations include factoring out a GCF, factoring a difference of squares, using the square root property, factoring a trinomial, and using the Quadratic Formula.

Factor out a GCF

Consider the function \(f(x)=2x^{2} +x\). If you were asked to solve \(f(x)=0\), it requires simple algebra:

\(\begin{align*}
x^{2} +x   &=0   &&\text{Factor}  \\
x(2x+1)      &=0     &&\text{Obtain solutions}\\
x = 0\        \text{ or }  &x = -\dfrac{1}{2}\\
\end{align*}\)

We use a similar process on trigonometric equations.

Example \(\PageIndex{24}\): Use GCF Factoring

Solve exactly: \(2 {\sin}^2 \theta+\sin \theta=0;\space 0≤\theta<2\pi\)

Solution

This problem should appear familiar as it is similar to a quadratic. Let \(\color{Cerulean}{\sin \theta=s}\). The equation becomes \(2s^2+s=0\). We begin by factoring:

\[\begin{align*}
2s^2+s&= 0\\
s(2s+1)&= 0\qquad \text {Set each factor equal to zero.}\\
\boxed{s= 0} & \quad 2s+1= 0\\
       & \quad \boxed{s= -\dfrac{1}{2}} \end{align*}\]

Then, substitute the original expression \(\color{Cerulean}{\sin \theta} \) back for \(\color{Cerulean}{s}\) in each of these solutions. Thus,

\(\begin{array} {c|cl}
s=0                &                s= -\dfrac{1}{2}          \\[2pt]
\sin \theta= 0            &               \sin \theta = -\dfrac{1}{2}            \\[2pt]
\theta= 0,\;\; \theta= \pi      &           \theta= \dfrac{7\pi}{6}, \;\;  \theta= \dfrac{11\pi}{6}    \\[2pt]
\end{array}\)

The solutions within the domain \(0≤\theta<2\pi\) are \(\theta=0,\pi,\dfrac{7\pi}{6},\dfrac{11\pi}{6}\).

As one gets more familiar with factoring trig expressions, you may prefer not to substitute, in which case we can solve the equation more directly:

\(\begin{align*}
\sin (t)\left(2\sin (t)+1\right)=0 \qquad\\
\sin (t)=0 \quad \text{ or  }   \quad 2\sin (t)+1=0\\\
\end{align*}\)

Analysis

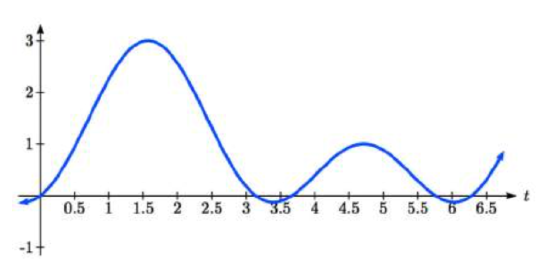We could check these answers are reasonable by graphing the function and comparing the zeros. We can see the solutions on the graph in the figure to the right. On the interval \(0≤\theta<2\pi\), the graph crosses the \(x\)-axis four times, at the solutions noted. Notice that trigonometric equations that are in quadratic form can yield up to four solutions instead of the expected two that are found with quadratic equations. In this example, each solution (angle) corresponding to a positive sine value will yield two angles that would result in that value.

 Try It  \(\PageIndex{24}\)

Solve the quadratic equation \(2 \cos^2 \theta+\cos \theta=0\).

Answer

\(\dfrac{\pi}{2}, \space \dfrac{2\pi}{3}, \space \dfrac{4\pi}{3}, \space \dfrac{3\pi}{2}\)

Factor a Difference of Squares

When confronted with two terms that are both perfect squares and one is subtracted from the other, we have what is called a difference of squares. In general, the difference of squares formula is \(a^2−b^2=(a−b)(a+b)\).

Example \(\PageIndex{25}\): Use the Difference of Squares

Solve: \(4{cos}^2 \theta−1 = 0\), \(0≤\theta<2\pi\).

Solution

Notice that both the coefficient and the trigonometric expression in the first term are squared, and the square of the number 1 is 1. This is a difference of squares.

\( 4{\cos}^2 \theta-1 = 0 \)
\( {(2\cos \theta)}^2-1 = 0 \)
\( (2\cos \theta-1)(2\cos \theta+1) = 0 \)

\(\begin{array}{c|c}
2\cos \theta=1 \quad & \quad 2\cos \theta=-1  \\
\cos \theta=\dfrac{1}{2} \quad & \quad \cos \theta=-\dfrac{1}{2}  \\
\theta=\dfrac {\pi}{3},\; \theta=\dfrac {5\pi}{3} \quad & \quad \theta=\dfrac {2\pi}{3},\; \theta=\dfrac {4\pi}{3}
\end{array}\)

Solution Set: \( \left\{ \dfrac {\pi}{3},\; \dfrac {5\pi}{3},\; \dfrac {2\pi}{3},\; \dfrac {4\pi}{3} \right\} \)

 Try It  \(\PageIndex{25}\)

Solve: \(25−9{\sin}^2 \theta = 0\), \(0≤\theta<2\pi\).

Answer

\(25−9{\sin}^2 \theta=(5−3\sin \theta)(5+3\sin \theta) = 0\). Therefore, \( \sin \theta = \pm \dfrac{5}{3} \). However, because it is always true that \( -1 \le \sin \theta \le 1 \), this equation has no solution.

Example \(\PageIndex{26}\): Use the square root property 
 

Solve the problem exactly: \(2 {\sin}^2 \theta−1=0\), \(0≤\theta<2\pi\).

Solution

As this problem is not easily factored, we will solve using the square root property. First, we use algebra to isolate \(\sin \theta\). Then we will find the angles.

\[\begin{align*}
2 {\sin}^2 \theta-1&= 0\\
2 {\sin}^2 \theta&= 1\\
{\sin}^2 \theta&= \dfrac{1}{2}\\
\sqrt{ {\sin}^2 \theta }&= \pm \sqrt{ \dfrac{1}{2} }= \pm \dfrac{1}{\sqrt{2}}\\
\sin \theta&= \pm \dfrac{\sqrt{2}}{2}\\
\end{align*}\]

Solution Set: \( \dfrac{\pi}{4}, \space \dfrac{3\pi}{4},\space \dfrac{5\pi}{4}, \space \dfrac{7\pi}{4} \)

Factor a Trinomial

Example \(\PageIndex{27}\): Factor a trinomial

Solve: \(2{\cos}^2 \theta+\cos \theta−1\), \(0≤\theta<2\pi\).

Solution

Letting \(\cos \theta=c\), we can rewrite a simplified version of the expression as follows:

\(2c^2+c−1 = 0\)

This quadratic expression can be factored as \((2c+1)(c−1)\). Replacing \(c\) with \(\cos \theta\) in this factored form yields

\((2\cos \theta+1)(\cos \theta−1) = 0\)

\(\begin{array}{c|c}
2\cos \theta=-1 \quad & \quad \cos \theta=1  \\
\cos \theta=-\dfrac{1}{2} \quad & \quad \theta=0, \; \theta = \pi  \\
\theta=\dfrac {2\pi}{3},\; \theta=\dfrac {4\pi}{3} 
\end{array}\)

Solution Set: \( \left\{ 0, \; \pi, \;  \dfrac {2\pi}{3},\; \dfrac {4\pi}{3} \right\} \)

Example \(\PageIndex{28}\) 

Solve the quadratic in form equation exactly: \(2 {\sin}^2 \theta−3 \sin \theta+1=0\), \(0≤\theta<2\pi\).

Solution

We can factor using the AC grouping method or the Reverse Foil method. Initially replacing \(\sin \theta\) with \(s\) may also be helpful. Solution values of \(\theta\) can be found on the unit circle.

\( (2 \sin \theta-1)(\sin \theta-1) = 0 \\[2pt]\)
\(\begin{array}{c|c}
 2 \sin \theta-1= 0             \quad & \quad  \sin \theta-1= 0 \\
\sin \theta= \dfrac{1}{2}   \quad & \quad      \sin \theta= 1\\[2pt]
\theta = \dfrac {\pi}{6}, \dfrac{5\pi}{6}  \quad & \quad \theta=\dfrac{\pi}{2} 
\end{array}\)

Solution Set: \( \left\{ \dfrac {\pi}{6}, \;\; \dfrac{5\pi}{6}, \;\; \dfrac{\pi}{2} \right\} \)

Example \(\PageIndex{29}\) 

Solve the equation exactly: \(2 {\sin}^2 \theta−5 \sin \theta+3=0\), \(0≤\theta≤2\pi\).

Solution

Using grouping, this quadratic can be factored. Either make the real substitution, \(\sin \theta=u\),or imagine it, as we factor:

\( 2 {\sin}^2 \theta-5 \sin \theta+3   = 0\\
(2 \sin \theta-3)(\sin \theta-1)               = 0  \\[2pt] \)
\(\begin{array}{c|c}
2 \sin \theta-3= 0     \quad & \quad    \sin \theta-1= 0 \\
\sin \theta= \dfrac{3}{2} \;\; \text{ Impossible}           \quad & \quad     \sin \theta= 1  \\   
\end{array}\)

Solution Set: \( \left\{  \dfrac{\pi}{2}   \right\} \)

Always make sure to check all solutions on the given domain as some factors have no solution.

Example \(\PageIndex{30}\)

Solve \(3\sec ^{2} (t)-5\sec (t)-2=0\) for all solutions with \(0\le t<2\pi\).

Solution

If it is easier to for you to consider factoring without the trig function present, consider using a substitution \(u=\sec (t)\), resulting in \(3u^{2} -5u-2=0,\). When factored, this becomes  \(  (3u+1)(u-2)=0 \). Then,

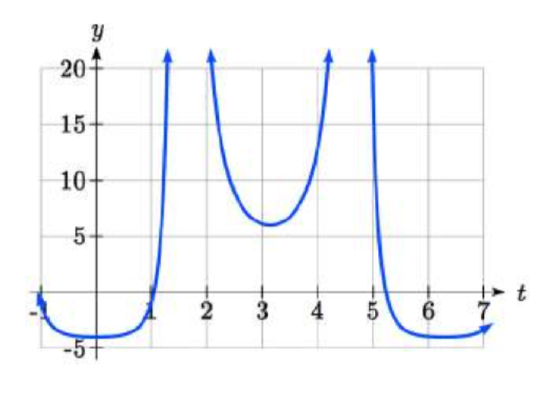\(\begin{array} {r|ll}
3u+1=0      &     u-2=0       & \text{Zero factor property}  \\
u=-\dfrac{1}{3}   &  u= 2         \\ 
\sec (t) = -\dfrac{1}{3}      &     \sec (t) =2    & \text{Substitute back}   \\
\cos (t) = -3      &     \cos (t) =\dfrac{1}{2}     & \text{Reciprocal Identity}  \\
\text{Impossible}      &     t= \dfrac{\pi}{3}, \;\;  t= \dfrac{5\pi}{3}   \\
\end{array}\)

By utilizing technology to graph \(f(t)=3\sec ^{2} (t)-5\sec (t)-2\), a look at a graph confirms there are only two zeros for this function on the interval [0, 2 \(\pi\)), which assures us that we didn’t miss anything.

 Try It  \(\PageIndex{31}\)

Solve \(2\sin ^{2} (t)+3\sin (t)+1=0\) for all solutions with \(0\le t<2\pi\).

Answer

\(2\sin ^{2} (t)+3\sin (t)+1=0 \\ \left(2\sin (t)+1\right)\left(\sin (t)+1\right)=0 \)

\(\begin{array} {rl|rll}
2\sin (t)+1&=0                &                \sin (t)+1&=0       &\text{Zero factor property}   \\[2pt]
\sin (t)&=-\dfrac{1}{2}               &              \sin (t)&=-1            \\[2pt]
t=\dfrac{7\pi }{6} ,&\dfrac{11\pi }{6}            &             t&=\dfrac{3\pi }{2}        
\end{array}\)

Solution Set: \( \left\{ \dfrac{7\pi }{6} ,\;\; \dfrac{3\pi }{2} ,\;\; \dfrac{11\pi }{6}  \right\} \)

Quadratic Formula

Example \(\PageIndex{32}\): Use the Quadratic Formula

Solve: \({\cos}^2 \theta+3 \cos \theta−1=0\), \(0≤\theta<2\pi\).

Solution

We begin by using substitution and replacing \(\cos \theta\) with \(x\). It is not necessary to use substitution, but it may make the problem easier to solve visually. Let \(\cos \theta=x\). We have

\(x^2+3x−1=0\)

The equation cannot be factored, so we will use the quadratic formula: \(x=\dfrac{−b\pm \sqrt{b^2−4ac}}{2a}\).

\(x= \dfrac{ -3\pm \sqrt{ {(-3)}^2-4 (1) (-1) } }{2} = \dfrac{-3\pm \sqrt{13}}{2}\)

Replace \(x\) with \(\cos \theta \) and solve.

\( \cos \theta = \dfrac{-3\pm \sqrt{13}}{2} \)

\( \theta = {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right) \)

Note that only the + sign is used. This is because we get an error when we solve \(\theta={\cos}^{−1}\left(\dfrac{−3−\sqrt{13}}{2}\right)\) on a calculator, since the domain of the inverse cosine function is \([ −1,1 ]\). However, there is a second solution:

\( \theta= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right) \approx 1.26 \)

This terminal side of the angle lies in quadrant I. Since cosine is also positive in quadrant IV, the second solution is

\( \theta = 2\pi-{\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right) \approx 5.02 \)

Use Identities to pre-process an Equation

Before a trigonometric equation can be solved, the equation must usually contain just one trigonometric function and one angle. In cases where there are two different trig functions in the equation, and one is a square of a trigonometric function, it is sometimes helpful apply a Pythagorean Identity to create an equation that has just one trig function in it.  The Pythagorean Identities, as well as some other identities we have learned so far, are listed below.

Definitions: IDENTITIES

Pythagorean Identities

\[\cos ^{2} (t)+\sin ^{2} (t)=1\qquad 1+\cot ^{2} (t)=\csc ^{2} (t)\qquad 1+\tan ^{2} (t)=\sec ^{2} (t) \nonumber \]

Reciprocal and Quotient Identities

\[\sec (t)=\dfrac{1}{\cos (t)}\qquad \csc (t)=\dfrac{1}{\sin (t)} \qquad \tan (t)=\dfrac{\sin (t)}{\cos (t)} \qquad \cot (t)=\dfrac{1}{\tan (t)} \nonumber \]

Example \(\PageIndex{33}\): Use an Identity

Solve the equation exactly using an identity: \(3 \cos \theta+3=2 {\sin}^2 \theta\), \(0≤\theta<2\pi\).

Solution

If we use a Pythagorean Identity to replace \(\sin^2 \theta\) with \(1-\cos^2 \theta \), we can obtain an equation that only has the cosine function in it:

\[\begin{align*}
3 \cos \theta+3&= 2 \color{Cerulean}{{\sin}^2 \theta}\\
3 \cos \theta+3&= 2\color{Cerulean}{(1-{\cos}^2 \theta)}\\
3 \cos \theta+3&= 2-2{\cos}^2 \theta\\
2 {\cos}^2 \theta+3 \cos \theta+1&= 0\\
(2 \cos \theta+1)(\cos \theta+1)&= 0\\
\end{align*}\]

\(\begin{array} {r|ll}
2 \cos \theta+1= 0                &              \cos \theta+1= 0  \\[2pt]
\cos (\theta)=-\dfrac{1}{2}               &              \cos \theta=-1            \\[2pt]
\theta= \dfrac{2\pi}{3},\space \dfrac{4\pi}{3}            &            \theta= \pi        
\end{array}\)

Our solutions are \(\theta=\dfrac{2\pi}{3},\space \dfrac{4\pi}{3},\space \pi\).

 Try It \(\PageIndex{34}\) 

Solve \({\sin}^2 \theta=2 \cos \theta+2\), \(0≤\theta≤2\pi\). [Hint: Make a substitution to express the equation only in terms of cosine.]

Answer

\(\cos \theta=−1\), \(\theta=\pi\)

The Pythagorean Identities become very useful whenever an equation involves a combination of sine and cosine functions.

Example \(\PageIndex{35}\)

Solve \(2\sin ^{2} (t)-\cos (t)=1\) for all solutions with \(0\le t<2\pi\).

Solution

Since this equation has a mix of sine and cosine functions, it becomes more complicated to solve. It is usually easier to work with an equation involving only one trig function. This is where we can use the Pythagorean Identity.

\[\begin{align*}
2 \; {\color{Cerulean}{\sin ^{2} (t)}} -\cos (t)  &=1  &&\text{Use the Pythagorean Identity:  }  \sin ^{2} (\theta )=1-\cos ^{2} (\theta )   \\
2 \; {\color{Cerulean}{\left(1-\cos ^{2} (t)\right)}} -\cos (t) &=1  &&\text{Distribute the 2}\\
2-2\cos ^{2} (t)-\cos (t)    &=1\\
\end{align*}\]

Since this is now quadratic in cosine, we rearrange the equation so one side is zero and factor.

\[\begin{align*}
-2\cos ^{2} (t)-\cos (t)+1   &=0   &&\text{Multiply by -1 to simplify the factoring}\\
2\cos ^{2} (t)+\cos (t)-1    &=0   &&\text{Factor}\\
\left(2\cos (t)-1\right)\left(\cos (t)+1\right)    & =0
\end{align*}\]

This product will be zero if either factor is zero, so we can break this into two separate cases and solve each independently.

\(\begin{array} {r|ll}
2\cos (t)-1=0                &              \cos (t)+1=0  \\[2pt]
 \cos (t)=\dfrac{1}{2}               &              \cos (t)=-1            \\[2pt]
 t=\dfrac{\pi }{3} \text{ or } t=\dfrac{5\pi }{3}            &            t=\pi       
\end{array}\)

The solutions are \( t = \dfrac{\pi }{3} ,\; \dfrac{5\pi }{3},\; \pi \). 

 Try It \(\PageIndex{36}\)

Solve \(2\sin ^{2} (t)=3\cos (t)\) for all solutions with \(0\le t<2\pi\).

Answer

\[\begin{align*}
2\left(1-\cos ^{2} (t)\right)   &=3\cos (t) \\
2\cos ^{2} (t)+3\cos (t)-2   &=0 \\
\left(2\cos (t)-1\right)\left(\cos (t)+2\right)   &=0
\end{align*}\]

\(2\cos (t)-1=0\) has two solutions, \(t=\dfrac{\pi }{3} ,\dfrac{5\pi }{3}\). \(\cos (t)+2=0\) has no solutions. 

In addition to the Pythagorean Identity, it is often necessary to rewrite the tangent, secant, cosecant, and cotangent as part of solving an equation.

Example \(\PageIndex{37}\)

Solve \(\tan (x)=3\sin (x)\) for all solutions with \(0\le x<2\pi\).

Solution

With a combination of tangent and sine, we might try rewriting tangent

\[\begin{align*}
\tan (x)   &=3\sin (x) \\
\dfrac{\sin (x)}{\cos (x)}    &=3\sin (x) &&\text{Multiply both sides by cosine}\\
\sin (x)   &=3\sin (x)\cos (x)
\end{align*}\]

At this point, you may be tempted to divide both sides of the equation by sin(\(x\)).

Resist the urge. When we divide both sides of an equation by a quantity, we are assuming the quantity is never zero. In this case, when sin(\(x\)) = 0 the equation is satisfied, so we’d lose those solutions if we divided by the sine.

To avoid this problem, we can rearrange the equation so that one side is zero (You technically can divide by sin(x), as long as you separately consider the case where sin(x) = 0. Since it is easy to forget this step, the factoring approach used in the example is recommended.).

\[\begin{align*}
\sin (x)-3\sin (x)\cos (x)   &=0 &&\text{Factor out sin(\(x\)) from both parts}\\
\sin (x)\left(1-3\cos (x)\right)   &=0 \\
\end{align*}\]

From here, we can see we get solutions when \(\sin (x)=0\) or \(1-3\cos (x)=0\).

\(\begin{array} {r|ll}
\sin (x)=0                &             1-3\cos (x)=0 \\
 x=0 \text{ or } x=\pi               &             \cos (x)=\dfrac{1}{3}            \\
            &           x=\cos ^{-1} \left(\dfrac{1}{3} \right)\approx 1.231 &\text{First solution (in QI)} \\[2pt]      
&            x=2\pi -1.231=5.052  &\text{Second solution in QIV}  
\end{array}\)

We have four solutions on \(0 \le x<2\pi\): \(x = 0,\; 1.231,\;  \pi ,\; 5.052\)

Example \(\PageIndex{38}\)

Solve \(\sec (\theta )=2\cos (\theta )\) to find the first four positive solutions.

Answer

\[\begin{align*}
\dfrac{1}{\cos (\theta )} &=2\cos (\theta )\\
\dfrac{1}{2} &=\cos ^{2} (\theta )\\
\cos (\theta ) &=\pm \sqrt{\dfrac{1}{2} } =\pm \dfrac{\sqrt{2} }{2}
\end{align*}\]

Solutions are: \(\theta =\dfrac{\pi }{4} ,\dfrac{3\pi }{4} ,\dfrac{5\pi }{4} ,\dfrac{7\pi }{4}\)

Example \(\PageIndex{39}\)

Solve \(\dfrac{4}{\sec ^{2} (\theta )} +3\cos \left(\theta \right)=2\cot \left(\theta \right)\tan \left(\theta \right)\) for all solutions with \(0\le \theta <2\pi\).

Solution

\[\begin{align*}
\dfrac{4}{\sec ^{2} (\theta )} +3\cos \left(\theta \right)   &=2\cot \left(\theta \right)\tan \left(\theta \right)\  &&\text{Use the reciprocal identities} \\
4\cos ^{2} (\theta )+3\cos (\theta )   &=2\dfrac{1}{\tan (\theta )} \tan (\theta )  &&\text{Simplify}\\
4\cos ^{2} \left(\theta \right)+3\cos \left(\theta \right)   &=2  &&\text{Subtract 2 from each side}\\
4\cos ^{2} \left(\theta \right)+3\cos \left(\theta \right)-2   &=0\\
\end{align*}\]

This does not appear to factor nicely so we use the quadratic formula, remembering that we are solving for \( \cos(\theta) \).

\[\cos (\theta )=\dfrac{-3\pm \sqrt{3^{2} -4(4)(-2)} }{2(4)} =\dfrac{-3\pm \sqrt{41} }{8}\nonumber\]

\(\begin{array} {r|ll}
\cos (\theta )=\dfrac{-3-\sqrt{41} }{8}                &             \cos (\theta )=\dfrac{-3+\sqrt{41} }{8} \\[2pt]
 \cos (\theta )=-1.175               &             \cos (\theta )=0.425           \\[2pt]
          \text{No solution }  &           \theta =\cos ^{-1} \left(0.425\right)=1.131 &\text{First solution (in QI)} \\[2pt]      
&            \theta =2\pi -1.131=5.152  &\text{Second solution in QIV}\\[2pt]  
\end{array}\)

Solutions are: \(\theta =1.131,\;  5.152\)

Applications

We will now apply these ideas to problems involving periodic behavior.

Example \(\PageIndex{40}\): Modeling an Equation and Sketching a Sinusoidal Graph to Fit Criteria

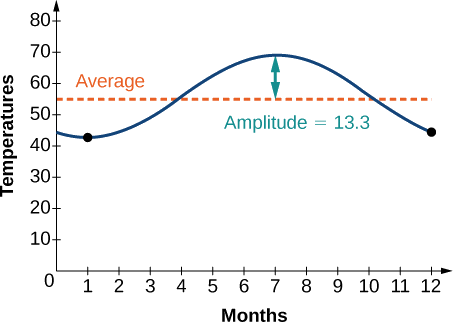
The average monthly temperatures for a small town in Oregon are given in Table \(\PageIndex{1}\). Find a sinusoidal function of the form \(y=A \sin (Bt−C)+D\) that fits the data (round to the nearest tenth) and sketch the graph.

Table \(\PageIndex{2}\)

Month	Temperature,\(^oF\)
January	42.5
February	44.5
March	48.5
April	52.5
May	58
June	63
July	68.5
August	69
September	64.5
October	55.5
November	46.5
December	43.5

Solution

Recall that amplitude is found using the formula

\[A=\dfrac{\text{largest value −smallest value}}{2} \nonumber\]

Thus, the amplitude is

\( |A|  = \dfrac{69−42.5}{2} =13.25 \)

The data covers a period of 12 months, so \(\frac{2π}{B}=12\) which gives \(B=\frac{2π}{12}=\frac{π}{6}\).

The vertical shift is found using the following equation.

\[D=\dfrac{\text{highest value+lowest value}}{2} \nonumber \]

Thus, the vertical shift is

\[\begin{align*} D &= \dfrac{69+42.5}{2} &=55.8 \end{align*}\]

So far, we have the equation \(y=13.3 \sin (\frac{π}{6}x−C)+55.8\).

To find the horizontal shift, we input the \(x\) and \(y\) values for the first month and solve for \(C\).

\[\begin{align*} 42.5 & =13.3 \sin (\frac{π}{6}(1)−C)+55.8 \\ −13.3 & =13.3 \sin (\frac{π}{6}−C) \\ −1 & =\sin (\frac{π}{6}−C) \;\;\;\;\;\;\;\; \sin θ=−1→ θ=−\frac{π}{2} \\ \frac{π}{6}−C=−\frac{π}{2} \\ \frac{π}{6}+\frac{π}{2} & =C \\ C &=\frac{2π}{3} \end{align*}\]

We have the equation \(y=13.3 \sin (\frac{π}{6}x−\frac{2π}{3})+55.8\). See the graph in Figure \(\PageIndex{9}\).

Figure \(\PageIndex{9}\)

 Important Topics of This Section

• Solving trig equations using known values
• Using substitution to solve equations
• Finding answers in one cycle or period vs. finding all possible solutions
• Methods for solving trig equations