6.4: Sum and Difference Identities
- Page ID
- 34930
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Use sum and difference formulas for sine, cosine, and tangent.
- Use sum and difference formulas to solve equations.
- Use sum and difference formulas to verify identities.
The trigonometric identities we will examine in this section can be traced to a Persian astronomer who lived around 950 AD, but the ancient Greeks discovered these same formulas much earlier and stated them in terms of chords. These are special equations or postulates, true for all values input to the equations, and with innumerable applications.
In this section, we will learn techniques that will enable us to solve problems such as the ones presented above. The formulas that follow will simplify many trigonometric expressions and equations. Keep in mind that, throughout this section, the term formula is used synonymously with the word identity.
Sum and Difference Formulas for Cosine
Finding the exact value of the sine, cosine, or tangent of an angle is often easier if we can rewrite the given angle in terms of two angles that have known trigonometric values. The sum and difference formulas for cosine are given below. We can use special angles and directly obtain the cosine of an angle that is the combination of known "special" angles. Alternatively, we may be a given trigonometric ratio and the quadrant the angle is in, and from that information, indirectly deduce the cosine of an angle described in this way.
Cosine: Sum and Difference Formulas
\[\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta \nonumber \]
\[\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta \nonumber \]
Proof of difference formula for cosines
First, we will prove the difference formula for cosines. Let’s consider two points on the unit circle illustrated in the figure to the right. Point \(P\) is at an angle \(\alpha\) from the positive \(x\)-axis with coordinates \((\cos \alpha,\sin \alpha)\) and point \(Q\) is at an angle of \(\beta\) from the positive \(x\)-axis with coordinates \((\cos \beta,\sin \beta)\). Note the measure of angle \(POQ\) is \(\alpha−\beta\).
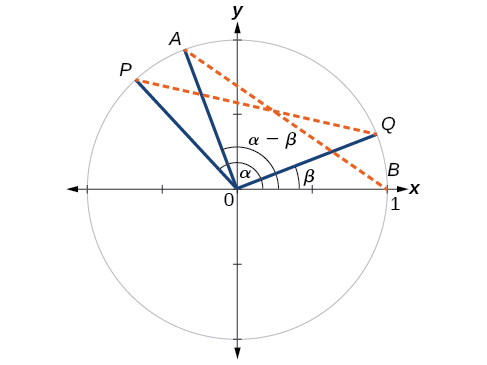Label two more points: \(A\) at an angle of \((\alpha−\beta)\) from the positive \(x\)-axis with coordinates \((\cos(\alpha−\beta),\sin(\alpha−\beta))\); and point \(B\) with coordinates \((1,0)\). Triangle \(POQ\) is a rotation of triangle \(AOB\) and thus the distance from \(P\) to \(Q\) is the same as the distance from \(A\) to \(B\).We can find the distance from \(P\) to \(Q\) using the distance formula.
\(\begin{align*}
d_{PQ}&= \sqrt{{(\cos \alpha - \cos \beta )}^2+{(sin \alpha - sin \beta )}^2}\\[4pt]
&= \sqrt{{\cos}^2 \alpha-2\cos \alpha \cos \beta+{\cos}^2 \beta+{\sin}^2 \alpha-2\sin \alpha \sin \beta+{\sin}^2 \beta} & & \text {}\ \\[4pt]
&= \sqrt{({\cos}^2 \alpha+{\sin}^2 \alpha)+({\cos}^2 \beta+{\sin}^2 \beta)-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta}\\[4pt]
&= \sqrt{1+1-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta}\\[4pt]
&= \sqrt{2-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta}\end{align*}\)
Similarly, using the distance formula we can find the distance from \(A\) to \(B\).
\(\begin{align*}
d_{AB}&= \sqrt{{(\cos(\alpha-\beta)-1)}^2+{(\sin(\alpha-\beta)-0)}^2}\\[4pt]
&= \sqrt{{\cos}^2(\alpha-\beta)-2\cos(\alpha-\beta)+1+{\sin}^2(\alpha-\beta)} & & \text {}\\[4pt]
&= \sqrt{({\cos}^2(\alpha-\beta)+{\sin}^2(\alpha-\beta))-2\cos(\alpha-\beta)+1}\\[4pt]
&= \sqrt{1-2\cos(\alpha-\beta)+1}\\[4pt]
&= \sqrt{2-2\cos(\alpha-\beta)}
\end{align*}\)
Equating these two distances, we get \( \sqrt{2-2\cos(\alpha-\beta)} = \sqrt{2-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta} \). If we then square both sides, subtract \(2\) from both sides and divide both sides by \(−2\), the result is the difference formula for cosine: \(\cos(\alpha-\beta) = \cos \alpha \cos \beta+\sin \alpha \sin \beta\).
Proof of sum formula for cosines
To derive the cosine of the sum of two angles, start with writing the sum of two angles as a difference, and use the difference formula we just derived.
\(\begin{align*}
\cos(\alpha + \beta) &= \cos \left( \alpha - (-\beta) \right) \\
&= \cos \alpha \cos (-\beta)+\sin \alpha \sin (-\beta) && \text{Use the Even/Odd Identities to remove the negative angle} \\
&= \cos \alpha \cos (\beta)-\sin \alpha \sin (-\beta) && \text{This is the sum formula for cosine}
\end{align*}\)
Example \(\PageIndex{1}\): Find the Exact Value for the Cosine of the Difference of Two Angles
Using the formula for the cosine of the difference of two angles, find the exact value of \(\cos\left(\dfrac{5\pi}{4}−\dfrac{\pi}{6}\right)\).
Solution
Begin by writing the formula for the cosine of the difference of two angles. Then substitute the given values.
\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos\left(\dfrac{5\pi}{4}-\dfrac{\pi}{6}\right)&= \cos\left(\dfrac{5\pi}{4}\right)\cos\left(\dfrac{\pi}{6}\right)+\sin\left(\dfrac{5\pi}{4}\right)\sin\left(\dfrac{\pi}{6}\right)\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{\sqrt{3}}{2}\right)-\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{1}{2}\right)\\[4pt] &= -\dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{-\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Keep in mind that we can always check the answer using a calculator in radian mode.
Try It \(\PageIndex{1}\):
Find the exact value of \(\cos\left(\dfrac{\pi}{3}−\dfrac{\pi}{4}\right)\).
- Answer
-
\(\dfrac{\sqrt{2}+\sqrt{6}}{4}\)
Example \(\PageIndex{2}\): Find the Exact Value for the Cosine of the Sum of Two Angles
Find the exact value of \(\cos(75°)\).
Solution
As \(75°=45°+30°\),we can evaluate \(\cos(75°)\) as \(\cos(45°+30°)\).
\[\begin{align*} \cos(\alpha+\beta)&= \cos \alpha \cos \beta -\sin \alpha \sin \beta\\[4pt] \cos(45^{\circ}+30^{\circ})&= \cos(45^{\circ})\cos(30^{\circ})-\sin(45^{\circ})\sin(30^{\circ})\\[4pt] &= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Keep in mind that we can always check the answer using a calculator in degree mode.
Analysis
Note that we could have also solved this problem using the fact that \( 75°=135°−60°\).
\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos(135^{\circ}-60^{\circ})&= \cos(135^{\circ})\cos(60^{\circ})+\sin(135^{\circ})\sin(60^{\circ})\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{1}{2}\right)+\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{\sqrt{3}}{2}\right)\\[4pt] &= -\dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{6}}{4}\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Try It \(\PageIndex{2}\)
Find the exact value of \(\cos(105°)\).
- Answer
-
\(\dfrac{\sqrt{2}-\sqrt{6}}{4}\)
Sum and Difference Formulas for Sine
The sum and difference formulas for sine can be derived in the same manner as those for cosine, and they resemble the cosine formulas.
Sine: Sum and Difference Formulas
\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\]
\[\sin(\alpha−\beta)=\sin \alpha \cos \beta−\cos \alpha \sin \beta\]
Proof of the sum and difference formulas for sine
The derivation for the sine of a sum of two angles can be shown using the Cofunction Identities and the formula for the cosine of the difference of two angles.
\(\begin{align*}
\sin(\alpha + \beta) &= \cos \left( \dfrac{\pi}{2} - (\alpha +\beta) \right) && \text{Cofunction Identity: }\sin A = \cos( \pi/2 - A) \\
&= \cos \left( \left(\dfrac{\pi}{2} - \alpha\right) -\beta \right) \\
&= \cos \left(\dfrac{\pi}{2} - \alpha\right) \cdot \cos \beta + \sin \left(\dfrac{\pi}{2} - \alpha\right) \cdot \sin \beta && \text{Cosine of a difference of angles formula}\\
&= \sin \alpha \cos \beta + \cos \alpha \sin \beta && \text{Cofunction Identity: } \cos( \pi/2 - A) = \sin A \\
\end{align*}\)
The derivation for the sine of a difference of two angles comes from using the formula for the sine of the sum of two angles.
\(\begin{align*}
\sin(\alpha - \beta) &= \sin (\alpha +(- \beta)) \\
&= \sin \alpha \cos (-\beta) + \cos \alpha \sin (- \beta) \\
&= \sin \alpha \cos \beta - \cos \alpha \sin \beta && \text{Even/Odd Properties } \\
\end{align*}\)
Example \(\PageIndex{3}\): Using Sum and Difference Identities to Evaluate the Difference of Angles
Use the sum and difference identities to evaluate the difference of the angles and show that part a equals part b.
- \(\sin(45°−30°)\)
- \(\sin(135°−120°)\)
Solution
- Let’s begin by writing the formula and substitute the given angles.
\[\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(45^{\circ}-30^{\circ})&= \sin(45^{\circ})\cos(30^{\circ})-\cos(45^{\circ})\sin(30^{\circ}) \end{align*}\]
Next, we need to find the values of the trigonometric expressions.
\(\sin(45°)=\dfrac{\sqrt{2}}{2}, \qquad \cos(30°)=\dfrac{\sqrt{3}}{2}, \qquad \cos(45°)=\dfrac{\sqrt{2}}{2}, \qquad \sin(30°)=\dfrac{1}{2}\)
Now we can substitute these values into the equation and simplify.
\( \sin(45°-30°)= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right) = \dfrac{\sqrt{6}-\sqrt{2}}{4} \)
- Again, we write the formula and substitute the given angles.
\[\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(135^{\circ}-120^{\circ})&= \sin(135^{\circ})\cos(120^{\circ})-\cos(135^{\circ})\sin(120^{\circ}) \end{align*}\]
Next, we find the values of the trigonometric expressions.
\(\sin(135°)=\dfrac{\sqrt{2}}{2}, \qquad \cos(120°)=-\dfrac{1}{2}, \qquad \cos(135°)=\dfrac{\sqrt{2}}{2}, \qquad \sin(120°)=\dfrac{\sqrt{3}}{2}\)
Now we can substitute these values into the equation and simplify.
\( \sin(135^{\circ}-120^{\circ})= \dfrac{\sqrt{2}}{2}\left(-\dfrac{1}{2}\right)-\left(-\dfrac{\sqrt{2}}{2}\right)\left (\dfrac{\sqrt{3}}{2}\right) = \dfrac{\sqrt{6}-\sqrt{2}}{4} \)
Example \(\PageIndex{4}\): Finding the Exact Value of an Expression Involving an Inverse Trigonometric Function
Find the exact value of \(\sin\left ({\cos}^{−1}\dfrac{1}{2}+{\sin}^{−1}\dfrac{3}{5}\right)\). Then check the answer with a graphing calculator.
Solution
The pattern displayed in this problem is \(\sin(\alpha+\beta)\), where \(\alpha={\cos}^{−1}\dfrac{1}{2}\) and \(\beta={\sin}^{−1}\dfrac{3}{5}\). Then we can write
\[\begin{align*}
\cos \alpha&= \dfrac{1}{2}, \quad 0\leq \alpha\leq \pi\\[4pt]
\sin \beta&= \dfrac{3}{5}, \quad - \dfrac{\pi}{2}\leq \beta\leq \dfrac{\pi}{2}\\[4pt]\end{align*}\]
We will use the Pythagorean identities to find \(\sin \alpha\) and \(\cos \beta\)
\( \sin \alpha = \sqrt{1-{\cos}^2 \alpha} = \sqrt{1-\dfrac{1}{4}} = \sqrt{\dfrac{3}{4}} = \dfrac{\sqrt{3}}{2} \)
\( \cos \beta = \sqrt{1-{\sin}^2 \beta} = \sqrt{1-\dfrac{9}{25}} = \sqrt{\dfrac{16}{25}} = \dfrac{4}{5} \)
Using the sum formula for sine,
\[\begin{align*} \sin \left({\cos}^{-1}\dfrac{1}{2}+{\sin}^{-1}\dfrac{3}{5}\right)&= \sin(\alpha+\beta)\\[4pt] &= \sin \alpha \cos \beta+\cos \alpha \sin \beta\\[4pt] &= \dfrac{\sqrt{3}}{2}\cdot \dfrac{4}{5}+\dfrac{1}{2}\cdot \dfrac{3}{5}\\[4pt] &= \dfrac{4\sqrt{3}+3}{10} \end{align*}\]
Sum and Difference Formulas for Tangent
Finding the sum of two angles formula for tangent involves taking quotient of the sum formulas for sine and cosine and simplifying. Recall, \(\tan x=\dfrac{\sin x}{\cos x}\), when \(\cos x≠0\).
\[\begin{align*}
\tan\left (\alpha+\beta\right)&= \dfrac{\sin\left (\alpha+\beta\right )}{\cos(\alpha+\beta)}\\[6pt]
&= \dfrac{\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\cos \alpha \cos \beta-\sin \alpha \sin \beta}\\[6pt]
&= \dfrac{ \;\;\; \dfrac{\sin \alpha \cos \beta+\cos \alpha \sin \beta \;\;\; }{\cos \alpha \cos \beta}}{\dfrac{\cos \alpha \cos \beta-\sin \alpha \sin \beta}{\cos \alpha \cos \beta}} = \dfrac{ \;\;\; \dfrac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta}+\dfrac{\cos \alpha \sin \beta \;\;\; }{\cos \alpha \cos \beta}}{\dfrac{\cos \alpha \cos \beta}{\cos \alpha \cos \beta}-\dfrac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}}\\[6pt]
&= \dfrac{ \;\;\; \dfrac{\sin \alpha}{\cos \alpha}+\dfrac{\sin \beta}{\cos \beta} \;\;\; }{1-\dfrac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}}\\[6pt]
&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}
\end{align*}\]
We can derive the difference formula for tangent by using the sum formula above, plus the Odd/Even Identity for tangent.
Tangent: Sum and Difference Formulas
\[\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1−\tan \alpha \tan \beta}\]
\[\tan(\alpha-\beta)=\dfrac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}\]
Example \(\PageIndex{5}\): Finding the Exact Value of an Expression Involving Tangent
Find the exact value of \(\tan\left(\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)\).
Solution
Let’s first write the sum formula for tangent and then substitute the given angles into the formula.
\[\begin{align*}
\tan(\alpha+\beta)&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta} \\[4pt]
\tan\left(\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)&= \dfrac{\tan\left (\dfrac{\pi}{6}\right)+\tan\left (\dfrac{\pi}{4}\right )}{1-\left (\tan\left (\dfrac{\pi}{6}\right ) \right )\left (\tan\left (\dfrac{\pi}{4}\right )\right )}\end{align*}\]
Next, we determine the individual function values within the formula:
\[\tan\left (\dfrac{\pi}{6}\right )= \dfrac{1}{\sqrt{3}}, \quad \text{and} \quad \tan\left (\dfrac{\pi}{4}\right) = 1 \nonumber\]
So we have,
\[\begin{align*}\tan\left (\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)&= \dfrac{\dfrac{1}{\sqrt{3}}+1}{1-\left(\dfrac{1}{\sqrt{3}}\right )(1)}\\[6pt]
&= \dfrac{\dfrac{1+\sqrt{3}}{\sqrt{3}}}{\dfrac{\sqrt{3}-1}{\sqrt{3}}} && \text{Simplify the complex fraction}\\[6pt]
&= \dfrac{1+\sqrt{3}}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{\sqrt{3}-1}\\[6pt]
&= \dfrac{\sqrt{3}+1}{\sqrt{3}-1} && \text{Rationalize the denominator} \\[6pt]
&= \dfrac{\sqrt{3}+1}{\sqrt{3}-1} \cdot \dfrac{\sqrt{3}+1}{\sqrt{3}+1} && \text{Multiply out} \\[6pt]
&= \dfrac{3 + \sqrt{3}+ \sqrt{3}+1}{3 + \sqrt{3}- \sqrt{3}-1} && \text{Simplify} \\[6pt]
&= \dfrac{4 + 2\sqrt{3}}{2} = 2 + \sqrt{3} && \text{Simplify} \\[6pt]
\end{align*}\]
Try It \(\PageIndex{5}\):
Find the exact value of \(\tan\left (\dfrac{2\pi}{3}+\dfrac{\pi}{4}\right )\).
- Answer
-
\(\dfrac{1-\sqrt{3}}{1+\sqrt{3}}\)
Example \(\PageIndex{6}\): Finding Multiple Sums and Differences of Angles
Given \(\sin \alpha=\dfrac{3}{5}, \quad 0<\alpha<\dfrac{\pi}{2},\) and \(\cos \beta=−\dfrac{5}{13}, \quad \pi<\beta<\dfrac{3\pi}{2}\), find
a. \(\sin(\alpha+\beta)\) \( \qquad \) b. \(\cos(\alpha+\beta)\) \( \qquad\) c. \(\tan(\alpha+\beta)\) \(\qquad \) d. \(\tan(\alpha−\beta)\)
Solution
We can use the sum and difference formulas to identify the sum or difference of angles when the ratio of sine, cosine, or tangent is provided for each of the individual angles. To do so, we construct what is called a reference triangle to help find each component of the sum and difference formulas. Since these formulas will need the sine, cosine or tangent of angle \(\alpha\) and \(\beta\), we will determine them here and then use the results below.
|
Given \(\sin \alpha=\dfrac{3}{5}, \quad 0<\alpha<\dfrac{\pi}{2},\)
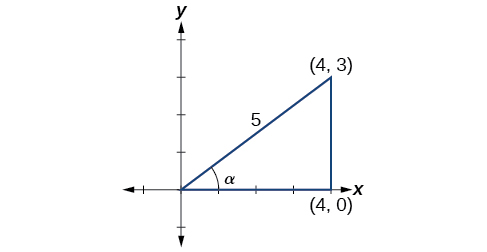
\(\sin \alpha=\dfrac{3}{5}\), \(\cos \alpha=\dfrac{4}{5}\), \(\tan \alpha=\dfrac{3}{4}\) |
Given \(\cos \beta=−\dfrac{5}{13}, \quad \pi<\beta<\dfrac{3\pi}{2}\)
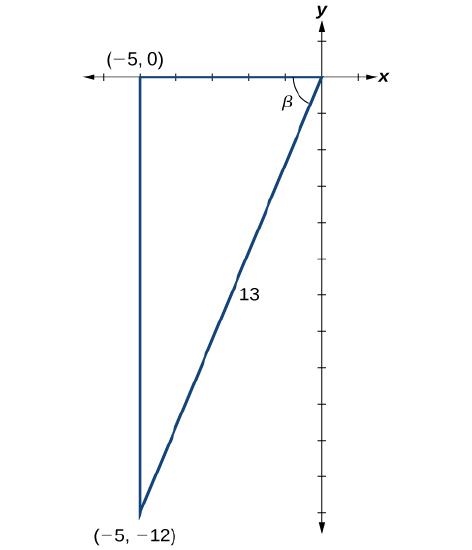
\(\sin \beta=\dfrac{-12}{13}\), \(\cos \beta=\dfrac{-5}{13}\), \(\tan \beta=\dfrac{12}{5}\) |
Now we are ready to use the formulas and perform the appropriate substitutions.
- To find \(\sin(\alpha+\beta)\),
\[\begin{align*} \sin(\alpha+\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta\\[4pt]
&= \left(\dfrac{3}{5}\right)\left(-\dfrac{5}{13}\right )+\left (\dfrac{4}{5}\right )\left(-\dfrac{12}{13}\right )
\quad = -\dfrac{15}{65}-\dfrac{48}{65} = -\dfrac{63}{65} \end{align*}\]
- Find \(\cos(\alpha+\beta)\)
\[\begin{align*} \cos(\alpha+\beta)&= \cos \alpha \cos \beta-\sin \alpha \sin \beta\\[4pt]
&= \left(\dfrac{4}{5}\right)\left(-\dfrac{5}{13}\right)-\left(\dfrac{3}{5}\right )\left(-\dfrac{12}{13}\right)
\quad = -\dfrac{20}{65}+\dfrac{36}{65} = \dfrac{16}{65} \end{align*}\]
- For \(\tan(\alpha+\beta)\)
\[\begin{align*}
\tan(\alpha+\beta)&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\\[6pt]
&= \dfrac{\dfrac{3}{4}+\dfrac{12}{5}}{1-\dfrac{3}{4}\left(\dfrac{12}{5}\right)}
\qquad= \dfrac{\dfrac{63}{20}}{-\dfrac{16}{20}}
= -\dfrac{63}{16}
\end{align*}\]
- To find \(\tan(\alpha−\beta)\)
\[\begin{align*}
\tan(\alpha-\beta)&= \dfrac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}\\[6pt]
&= \dfrac{\dfrac{3}{4}-\dfrac{12}{5}}{1+\dfrac{3}{4}\left(\dfrac{12}{5}\right)}
\qquad= \dfrac{-\dfrac{33}{20}}{\dfrac{56}{20}}= -\dfrac{33}{56}
\end{align*}\]
Use Sum and Difference Formulas to Solve Equations
These identities can also be used to solve equations.
Example \(\PageIndex{7}\)
Solve \(\sin (x)\sin (2x)+\cos (x)\cos (2x)=\dfrac{\sqrt{3} }{2}\).
Solution
By recognizing the left side of the equation as the result of the difference of angles identity for cosine, we can simplify the equation
\[\begin{align*}
\cos (x)\cos (2x) + \sin (x)\sin (2x) &=\dfrac{\sqrt{3} }{2} &&\text{Apply the difference of angles identity}\\[2pt]
\cos (x-2x)&=\dfrac{\sqrt{3} }{2} \\[2pt]
\cos (-x)&=\dfrac{\sqrt{3} }{2} &&\text{Use the negative angle identity}\\[2pt]
\cos (x)&=\dfrac{\sqrt{3} }{2}
\end{align*}\]
Since this is a special cosine value, so we can quickly write the answers: \( x=\dfrac{\pi }{6} +2\pi k \text{ and } x=\dfrac{11\pi }{6} +2\pi k\), where \(k\) is any integer
Use Sum and Difference Formulas to Verify Identities
Verifying an identity means demonstrating that the equation holds for all values of the variable. It helps to be very familiar with the identities or to have a list of them accessible while working the problems.
Example \(\PageIndex{8A}\): Verifying an Identity Involving Sine
Verify the identity \(\sin(\alpha+\beta)+\sin(\alpha−\beta)=2\sin \alpha \cos \beta\).
Solution
We see that the left side of the equation includes the sines of the sum and the difference of angles.
\(\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\)
\(\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta\)
We can rewrite each using the sum and difference formulas.
\[\begin{align*} \sin(\alpha+\beta)+\sin(\alpha-\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta+\sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] &= 2\sin \alpha \cos \beta \end{align*}\]
We see that the identity is verified.
Example \(\PageIndex{8B}\): Verifying an Identity Involving Tangent
Verify the following identity.
\(\dfrac{\sin(\alpha−\beta)}{\cos \alpha \cos \beta}=\tan \alpha−\tan \beta\)
Solution
We can begin by rewriting the numerator on the left side of the equation.
\[\begin{align*} \dfrac{\sin(\alpha-\beta)}{\cos \alpha \cos \beta}&= \dfrac{\sin \alpha \cos \beta-\cos \alpha \sin \beta}{\cos \alpha \cos \beta} & & \text{Split fraction apart}\\[4pt]
&= \dfrac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta}-\dfrac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta}& & \text{Cancel} \\[4pt]
&= \dfrac{\sin \alpha}{\cos \alpha}-\dfrac{\sin \beta}{\cos \beta} & & \text{Rewrite in terms of tangent} \\[4pt]
&= \tan \alpha-\tan \beta \end{align*}\]
Try It \(\PageIndex{8}\):
Verify the identity: \(\tan(\pi−\theta)=−\tan \theta\).
- Answer
-
\[\begin{align*} \tan(\pi-\theta)&= \dfrac{\tan(\pi)-\tan \theta}{1+\tan(\pi)\tan \theta}\\[4pt] &= \dfrac{0-\tan \theta}{1+0\cdot \tan \theta}\\[4pt] &= -\tan \theta \end{align*}\]
Applications of Sum and Difference Formulas
Example \(\PageIndex{9A}\): Using Sum and Difference Formulas to Solve an Application Problem
Let \(L_1\) and \(L_2\) denote two non-vertical intersecting lines, and let \(θ\) denote the acute angle between \(L_1\) and \(L_2\). See Figure \(\PageIndex{7}\). Show that
\(\tan \theta=\dfrac{m_2-m_1}{1+m_1m_2}\)
where \(m_1\) and \(m_2\) are the slopes of \(L_1\) and \(L_2\) respectively. (Hint: Use the fact that \(\tan \theta_1=m_1\) and \(\tan \theta_2=m_2\).)
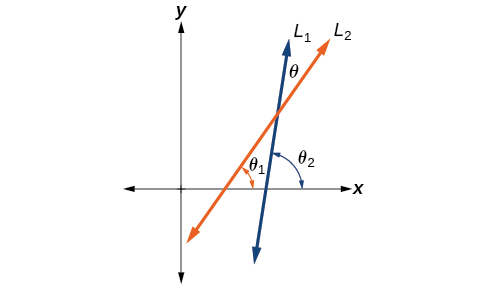
Solution
Observe that \(\theta_1 + (180^{\circ} - \theta_2) +\theta = 180^{\circ}\). Thus \(\theta = \theta_2 - \theta_1\). To find \(\theta\), use the difference formula for tangent, plus the knowledge that the tangent of an angle is the slope of the terminal side of that angle when it is placed in standard position.
\[\begin{align*} \tan \theta&= \tan(\theta_2-\theta_1)\\[4pt] &= \dfrac{\tan \theta_2-\tan \theta_1}{1+\tan \theta_1 \tan \theta_2}\\[4pt] &= \dfrac{m_2-m_1}{1+m_1m_2} \end{align*}\]
Example \(\PageIndex{9B}\): Investigating a Guy-wire Problem
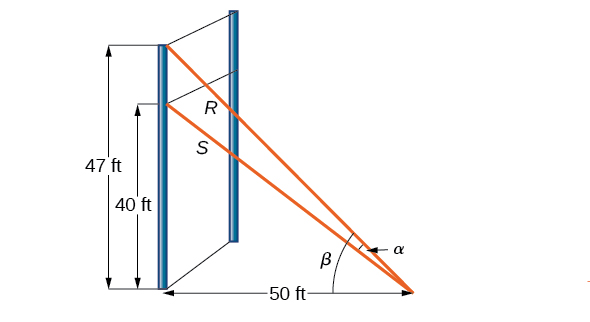
For a climbing wall, a guy-wire \(R\) is attached \(47\) feet high on a vertical pole. Added support is provided by another guy-wire \(S\) attached \(40\) feet above ground on the same pole. If the wires are attached to the ground \(50\) feet from the pole, find the angle \(\alpha\) between the wires. See Figure \(\PageIndex{8}\).
Solution
Let’s first summarize the information we can gather from the diagram. As only the sides adjacent to the right angle are known, we can use the tangent function. Notice that \(\tan \beta=\dfrac{47}{50}\), and \(\tan(\beta−\alpha)=\dfrac{40}{50}=\dfrac{4}{5}\). We can then use difference formula for tangent.
\[\tan(\beta-\alpha) = \dfrac{\tan \beta-\tan \alpha}{1+\tan \beta \tan \alpha} \nonumber \]
Now, substituting the values we know into the formula, we have,
\[\begin{align*} \dfrac{4}{5}&= \dfrac{\;\; \dfrac{47}{50}-\tan \alpha \;\;}{1+\dfrac{47}{50}\tan \alpha}\\[4pt]
4\left(1+\dfrac{47}{50}\tan \alpha\right)&= 5\left(\dfrac{47}{50}-\tan \alpha\right)\end{align*}\]
Use the distributive property, and then simplify the functions.
\[\begin{align*} 4(1)+4\left(\dfrac{47}{50}\right)\tan \alpha &= 5\left(\dfrac{47}{50}\right)-5\tan \alpha\\[4pt]
4+3.76\tan \alpha&= 4.7-5\tan \alpha\\[4pt]
5\tan \alpha+3.76\tan \alpha&= 0.7\\[4pt]
8.76 \tan \alpha&= 0.7\\[4pt]
\tan \alpha&\approx 0.07991\\[4pt]
\tan^{-1}(0.07991)&\approx .079741 \text{ radians or } 4.57^{\circ} \end{align*}\]
Key Equations
| Sum and Difference Formulas for Cosine | \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\) | \(\cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
| Sum and Difference Formulas for Sine | \(\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\) | \(\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta\) |
| Sum and Difference Formulas for Tangent | \(\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\) | \(\tan(\alpha-\beta)=\dfrac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}\) |
|
Cofunction identities |
\(\sin \theta=\cos\left(\dfrac{\pi}{2}-\theta\right)\) \(\cos \theta=\sin\left(\dfrac{\pi}{2}-\theta\right)\) \(\tan \theta=\cot\left(\dfrac{\pi}{2}-\theta\right)\) |
\(\cot \theta=\tan\left(\dfrac{\pi}{2}-\theta\right)\) \(\sec \theta=\csc\left(\dfrac{\pi}{2}-\theta\right)\) \(\csc \theta=\sec\left(\dfrac{\pi}{2}-\theta\right)\) |
Key Concepts
- The sum formula for cosines states that the cosine of the sum of two angles equals the product of the cosines of the angles minus the product of the sines of the angles. The difference formula for cosines states that the cosine of the difference of two angles equals the product of the cosines of the angles plus the product of the sines of the angles.
- The sum and difference formulas can be used to find the exact values of the sine, cosine, or tangent of an angle.
- The sum formula for sines states that the sine of the sum of two angles equals the product of the sine of the first angle and cosine of the second angle plus the product of the cosine of the first angle and the sine of the second angle. The difference formula for sines states that the sine of the difference of two angles equals the product of the sine of the first angle and cosine of the second angle minus the product of the cosine of the first angle and the sine of the second angle.
- The sum formula for tangent states that the tangent of the sum of two angles equals the sum of the tangents of the angles divided by \(1\) minus the product of the tangents of the angles. The difference formula for tangent states that the tangent of the difference of two angles equals the difference of the tangents of the angles divided by \(1\) plus the product of the tangents of the angles.
- The Pythagorean Theorem along with the sum and difference formulas can be used to find multiple sums and differences of angles.
- The cofunction identities apply to complementary angles and pairs of reciprocal functions.
- Sum and difference formulas are useful in verifying identities.
- Application problems are often easier to solve by using sum and difference formulas.
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.