7.2e: Exercises - Law of Cosines
- Page ID
- 68257
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)For all exercises below, assume \(\alpha\) or \(A\) is the angle opposite side \(a\), \(\beta\) or \(B\) is the angle opposite side \(b\), and \(\gamma\) or \(C\) is the angle opposite side \(c\).
A: Concepts
Exercise \(\PageIndex{A}\)
1) If you are looking for a missing side of a triangle, what do you need to know when using the Law of Cosines?
2) If you are looking for a missing angle of a triangle, what do you need to know when using the Law of Cosines?
3) Explain what \(s\) represents in Heron’s formula.
4) Explain the relationship between the Pythagorean Theorem and the Law of Cosines.
5) When must you use the Law of Cosines instead of the Pythagorean Theorem?
- Answers to odd exercises.
-
1. two sides and the angle opposite the missing side.
3. \(s\) is the semi-perimeter, which is half the perimeter of the triangle.
5. The Law of Cosines must be used for any oblique (non-right) triangle.
B: Find a side or an angle
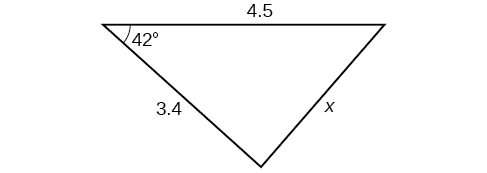
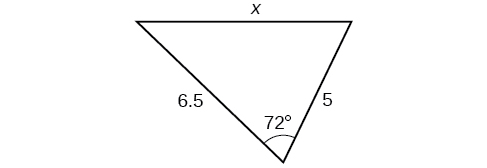
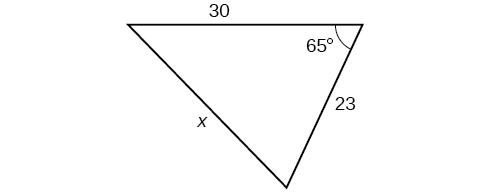
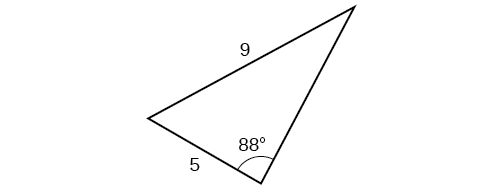
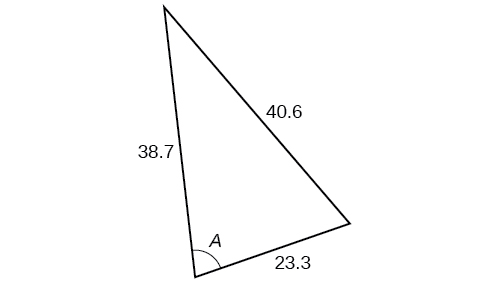
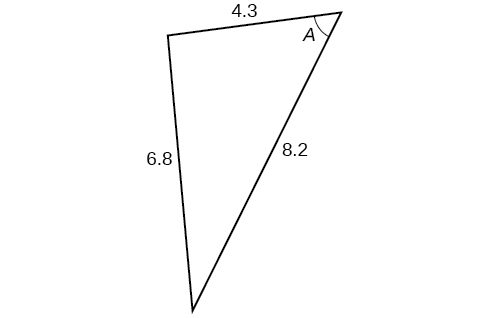
Exercise \(\PageIndex{A}\)
\( \bigstar \) If possible, solve each triangle for the unknown side. Round to the nearest tenth.
|
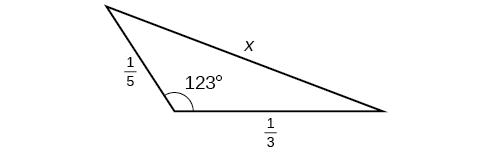
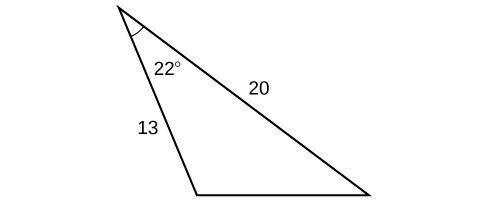
7) \(\alpha =120^{\circ}, b=6, c=7\) 8) \(\alpha =115^{\circ}, b=18, c=23\) 9) \(\gamma =41.2^{\circ}, a=2.49, b=3.13\) 10) \(\beta =58.7^{\circ}, a=10.6, c=15.7\) 11) \(\gamma =113^{\circ}, b=10, c=32\) |
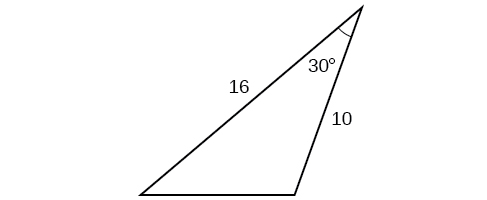
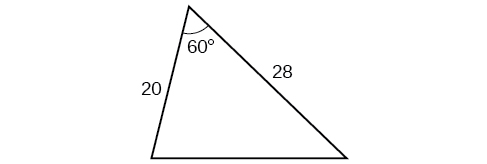
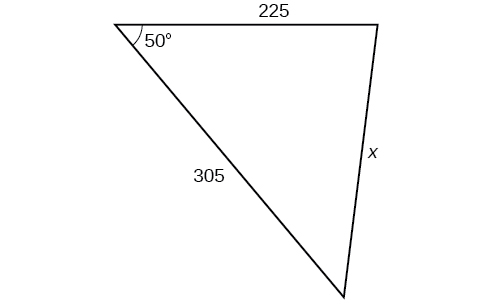
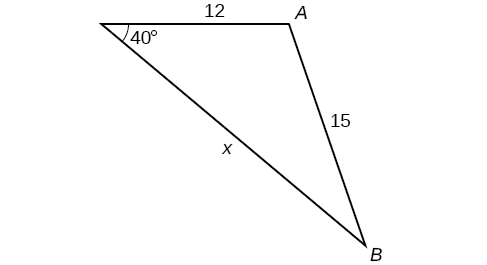
12) \(\alpha =119^{\circ}, a=26, b=14\) 13) \(\alpha =43.1^{\circ}, a=184.2, b=242.8\) 14) \(\alpha =36^{\circ}, a=22, b=26\) 15) \(\beta =50^{\circ}, a=105, b=45\) 16) \(\beta =67^{\circ}, a=49, b=38\) |
|
17) |
18) |
|
19) |
20) |
|
21) |
22) |
|
23) |
24) |
|
25) |
26) |
- Answers to odd exercises.
-
7. \(11.3 \qquad \) 9. \(2.1 \qquad \) 11. \(26.7 \qquad \) 13. \(257.3\) or \(97.2 \qquad \) 15. not possible.
17. \(3.0 \qquad \) 19. \(29.1 \qquad \) 21. \(0.5 \qquad \) 23. \(25.0 \qquad\) 25. \(9.3\)
\( \bigstar \) Use the Law of Cosines to solve for the missing angle of the oblique triangle. Round to the nearest tenth.
|
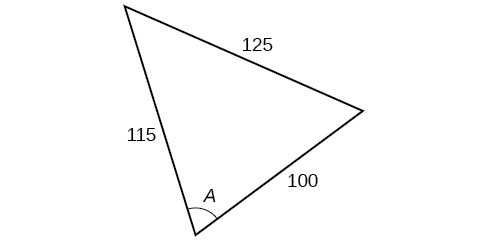
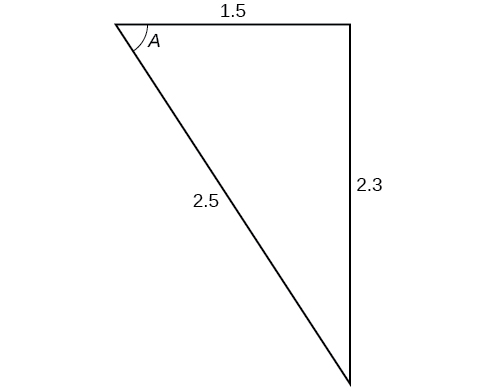
32) \(a=42, b=19, c=30\); find angle \(A\). 33) \(a=14, b=13, c=20\); find angle \(C\). 34) \(a=16, b=31, c=20\); find angle \(B\). |
35) \(a=13, b=22, c=28\); find angle \(A\). 36) \(a=108, b=132, c=160\); find angle \(C\). |
|
37)
|
38)
|
|
39)
|
40)
|
- Answers to odd exercises.
-
33. \(95.5^{\circ} \qquad \) 35. \(26.9^{\circ} \qquad \) 37. \(70.7^{\circ} \qquad \) 39. \(77.4^{\circ}\)
C: Solve a Triangle
Exercise \(\PageIndex{B}\)
\( \bigstar \) Solve the triangle. Round to the nearest tenth.
|
41. \(B=88^{\circ}, a=4.4, c=5.2\) 42. \(C=121^{\circ}, a=21, b=37\) 43. \(A=35^{\circ}, b=8, c=11\) 44. \(B=43^{\circ}, a=48, c=32\) |
47.  |
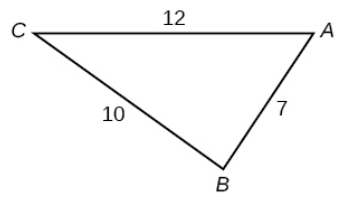48) \(a=13, b=11, c=15\) 49) \(a=3.1, b=3.5, c=5\) 50) \(a=25, b=51, c=29\) |
- Answers to odd exercises.
-
41. \(A\approx 41.1^{\circ}, C\approx 50.9^{\circ}, b\approx 6.7 \quad \)
43. \(B\approx 45.9^{\circ}, C\approx 99.1^{\circ}, a\approx 6.4 \quad \)
47. \(A\approx 56.4^{\circ}, B\approx 88.0^{\circ}, C\approx 35.7\)
49. \(A\approx 37.8^{\circ}, B\approx 43.8^{\circ}, C\approx 98.4\)
D: Extensions
Exercise \(\PageIndex{D}\)
52) A parallelogram has sides of length \(16\) units and \(10\) units. The shorter diagonal is \(12\) units. Find the measure of the longer diagonal.
53) The sides of a parallelogram are \(11\) feet and \(17\) feet. The longer diagonal is \(22\) feet. Find the length of the shorter diagonal.
54) The sides of a parallelogram are \(28\) centimeters and \(40\) centimeters. The measure of the larger angle is\(100^{\circ}\). Find the length of the shorter diagonal.
|
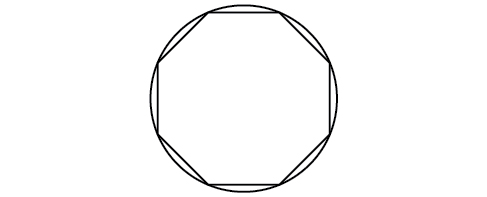
55) A regular octagon is inscribed in a circle with a radius of \(8\) inches. (See Figure below.) Find the perimeter of the octagon.
|
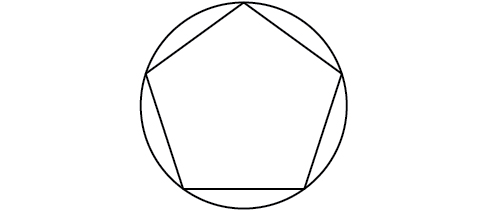
56) A regular pentagon is inscribed in a circle of radius \(12\) cm. (See Figure below.) Find the perimeter of the pentagon. Round to the nearest tenth of a centimeter.
|
\( \bigstar \) Suppose that \(x^2=25+36-60\cos(52)\) represents the relationship of three sides of a triangle and the cosine of an angle.
57) Draw the triangle.
58) Find the length of the third side
- Answers to odd exercises.
- 53. \(18.3 \qquad\) 55. \(48.98\)
57.
E: Real-World Applications
Exercise \(\PageIndex{E}\)
|
62) A surveyor has taken the measurements shown in the Figure below. Find the distance across the lake. Round answers to the nearest tenth. 
|
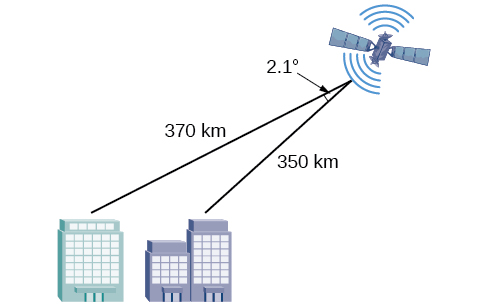
63) A satellite calculates the distances and angle shown in the Figure below (not to scale). Find the distance between the two cities. Round answers to the nearest tenth.
|
64) An airplane flies \(220\) miles with a heading of \(40^{\circ}\), and then flies \(180\) miles with a heading of \(170^{\circ}\). How far is the plane from its starting point, and at what heading? Round answers to the nearest tenth. |
|
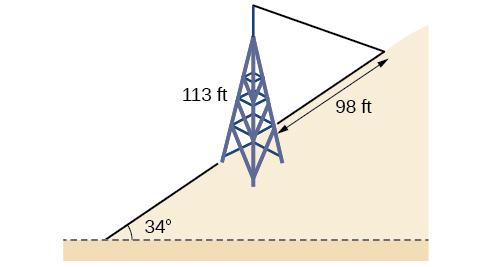
65) A \(113\)-foot tower is located on a hill that is inclined \(34^{\circ}\) to the horizontal, as shown in the Figure below. A guy-wire is to be attached to the top of the tower and anchored at a point \(98\) feet uphill from the base of the tower. Find the length of wire needed.
|
66) Two ships left a port at the same time. One ship traveled at a speed of \(18\) miles per hour at a heading of \(320^{\circ}\). The other ship traveled at a speed of \(22\) miles per hour at a heading of \(194^{\circ}\). Find the distance between the two ships after \(10\) hours of travel.
|
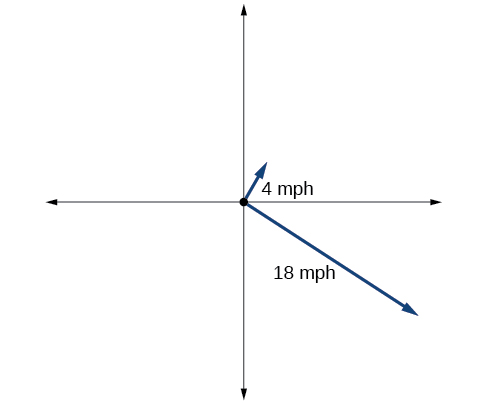
67) The graph in the Figure below represents two boats departing at the same time from the same dock. The first boat is traveling at \(18\) miles per hour at a heading of \(327^{\circ}\) and the second boat is traveling at \(4\) miles per hour at a heading of \(60^{\circ}\). Find the distance between the two boats after \(2\) hours.
|
68) A triangular swimming pool measures \(40\) feet on one side and \(65\) feet on another side. These sides form an angle that measures \(50^{\circ}\). How long is the third side (to the nearest tenth)?
69) A pilot flies in a straight path for \(1\) hour \(30\) min. She then makes a course correction, heading \(10^{\circ}\) to the right of her original course, and flies \(2\) hours in the new direction. If she maintains a constant speed of \(680\) miles per hour, how far is she from her starting position?
70) Los Angeles is \(1,744\) miles from Chicago, Chicago is \(714\) miles from New York, and New York is \(2,451\) miles from Los Angeles. Draw a triangle connecting these three cities, and find the angles in the triangle.
71) Philadelphia is \(140\) miles from Washington, D.C., Washington, D.C. is \(442\) miles from Boston, and Boston is \(315\) miles from Philadelphia. Draw a triangle connecting these three cities and find the angles in the triangle.
72) Two planes leave the same airport at the same time. One flies at \(20^{\circ}\) east of north at \(500\) miles per hour. The second flies at \(30^{\circ}\) east of south at \(600\) miles per hour. How far apart are the planes after \(2\) hours?
73) Two airplanes take off in different directions. One travels \(300\) mph due west and the other travels \(25^{\circ}\) west of north at \(420\) mph. After \(90\) minutes, how far apart are they, assuming they are flying at the same altitude?
74) A parallelogram has sides of length \(15.4\) units and \(9.8\) units. Its area is \(72.9\) square units. Find the measure of the longer diagonal.
- Answers to odd exercises.
-
63. \(24.0 \) km \(\quad\) 65. \(99.9\) ft \(\quad\) 67. \(37.3\) miles \(\quad\) 69. \(2371\) miles \(\quad\) 71.
\(\quad\) 73. \(599.8\) miles .