3.2: The Derivative as a Function
( \newcommand{\kernel}{\mathrm{null}\,}\)
As we have seen, the derivative of a function at a given point gives us the rate of change or slope of the tangent line to the function at that point. If we differentiate a position function at a given time, we obtain the velocity at that time. It seems reasonable to conclude that knowing the derivative of the function at every point would produce valuable information about the behavior of the function. However, the process of finding the derivative at even a handful of values using the techniques of the preceding section would quickly become quite tedious. In this section we define the derivative function and learn a process for finding it.
Derivative Functions
The derivative function gives the derivative of a function at each point in the domain of the original function for which the derivative is defined. We can formally define a derivative function as follows.
Definition: derivative function
Let
A function
In the next few examples we use Equation to find the derivative of a function.
Example
Find the derivative of
Solution
Start directly with the definition of the derivative function.
| Substitute |
|
| Multiply numerator and denominator by |
|
| Multiply the numerators and simplify. | |
| Cancel the |
|
| Evaluate the limit |
Example
Find the derivative of the function
Solution
Follow the same procedure here, but without having to multiply by the conjugate.
| Substitute |
|
| Expand |
|
| Simplify | |
| Factor out |
|
| Cancel the common factor of |
|
| Evaluate the limit |
![]()
Find the derivative of
- Hint
-
Use Equation and follow the example.
- Answer
-
We use a variety of different notations to express the derivative of a function. In Example we showed that if
In place of
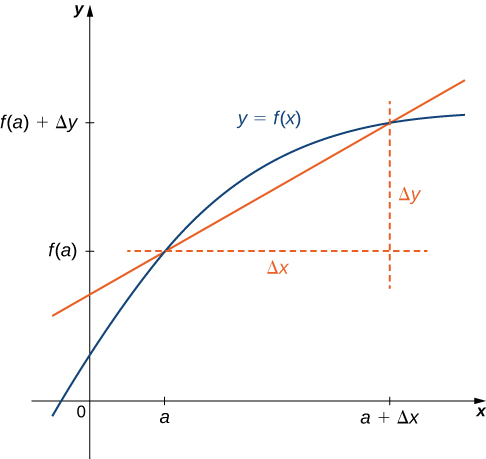
Figure
Graphing a Derivative
We have already discussed how to graph a function, so given the equation of a function or the equation of a derivative function, we could graph it. Given both, we would expect to see a correspondence between the graphs of these two functions, since
In Example we found that for
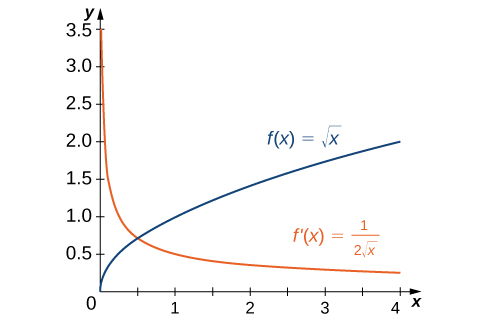
Figure
In Example we found that for
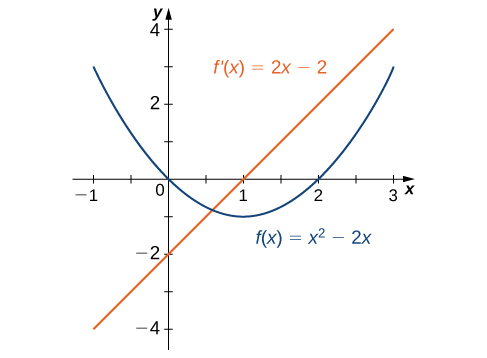
Figure
Example
Use the following graph of

Solution
The solution is shown in the following graph. Observe that

![]()
Sketch the graph of
- Hint
-
The graph of
- Answer
-
(0,+∞)
Derivatives and Continuity
Now that we can graph a derivative, let’s examine the behavior of the graphs. First, we consider the relationship between differentiability and continuity. We will see that if a function is differentiable at a point, it must be continuous there; however, a function that is continuous at a point need not be differentiable at that point. In fact, a function may be continuous at a point and fail to be differentiable at the point for one of several reasons.
Differentiability Implies Continuity
Let
Proof
If
We want to show that
Therefore, since
□
We have just proven that differentiability implies continuity, but now we consider whether continuity implies differentiability. To determine an answer to this question, we examine the function
This limit does not exist because
See Figure
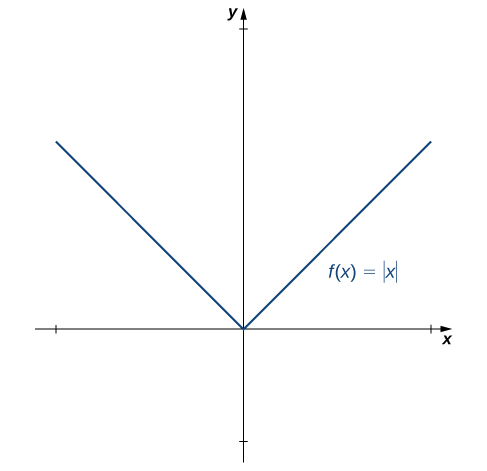
Figure
Let’s consider some additional situations in which a continuous function fails to be differentiable. Consider the function
Thus
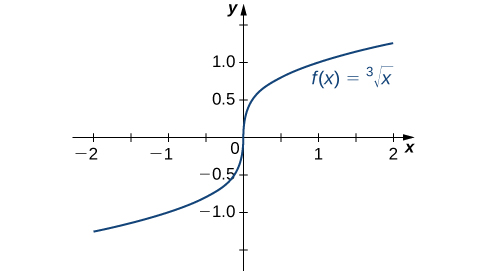
Figure
The function
This limit does not exist, essentially because the slopes of the secant lines continuously change direction as they approach zero (Figure).
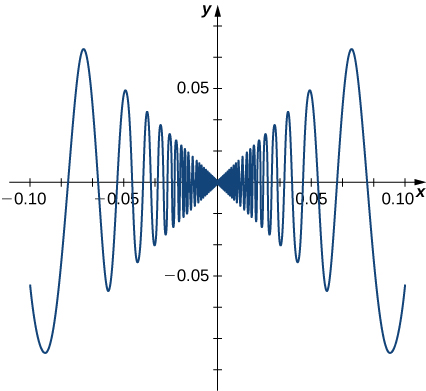
Figure
In summary:
- We observe that if a function is not continuous, it cannot be differentiable, since every differentiable function must be continuous. However, if a function is continuous, it may still fail to be differentiable.
- We saw that
- As we saw in the example of
- As we saw with
This last example is a valuable example to look over; however, you will not need to do these types of examples.
Example
A toy company wants to design a track for a toy car that starts out along a parabolic curve and then converts to a straight line (Figure

Figure
Solution
For the function to be continuous at
and
For the function to be differentiable at
must exist. Since
We also have
This gives us
![]()
Find values of a and b that make
- Hint
-
Use Example
- Answer
-
Key Concepts
- The derivative of a function
- The graph of a derivative of a function
- If a function is differentiable at a point, then it is continuous at that point. A function is not differentiable at a point if it is not continuous at the point, if it has a vertical tangent line at the point, or if the graph has a sharp corner or cusp.
- Higher-order derivatives are derivatives of derivatives, from the second derivative to the
Key Equations
- The derivative function
Glossary
- derivative function
- gives the derivative of a function at each point in the domain of the original function for which the derivative is defined
- differentiable at a
- a function for which
- differentiable on S
- a function for which
- differentiable function
- a function for which
- higher-order derivative
- a derivative of a derivative, from the second derivative to the nth derivative, is called a higher-order derivative
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


