5.5E: Exercises for Section 5.5
- Last updated
- Save as PDF
- Page ID
- 53723
1) Why is \(u\)-substitution referred to as a change of variable?
2) If \( f=g∘h\), when reversing the chain rule, \(\dfrac{d}{dx}(g∘h)(x)=g′(h(x))h′(x)\), should you take \( u=g(x)\) or \(u=h(x)?\)
- Answer
- \(u=h(x)\)
In exercises 3 - 7, verify each identity using differentiation. Then, using the indicated \(u\)-substitution, identify \(f\) such that the integral takes the form \(\displaystyle∫f(u)\,du.\)
3) \(\displaystyle ∫x\sqrt{x+1}\,dx=\frac{2}{15}(x+1)^{3/2}(3x−2)+C;\quad u=x+1\)
4) \(\displaystyle∫\frac{x^2}{\sqrt{x−1}}\,dx=\frac{2}{15}\sqrt{x−1}(3x^2+4x+8)+C,\quad (x>1);\quad u=x−1\)
- Answer
- \( f(u)=\dfrac{(u+1)^2}{\sqrt{u}}\)
5) \(\displaystyle∫x\sqrt{4x^2+9}\,dx=\frac{1}{12}(4x^2+9)^{3/2}+C;\quad u=4x^2+9\)
6) \(\displaystyle∫\frac{x}{\sqrt{4x^2+9}}\,dx=\frac{1}{4}\sqrt{4x^2+9}+C;\quad u=4x^2+9\)
- Answer
- \( du=8x\,dx;\quad f(u)=\frac{1}{8\sqrt{u}}\)
7) \(\displaystyle∫\frac{x}{(4x^2+9)^2}\,dx=−\frac{1}{8(4x^2+9)} + C;\quad u=4x^2+9\)
In exercises 8 - 17, find the antiderivative using the indicated substitution.
8) \(\displaystyle∫(x+1)^4\,dx;\quad u=x+1\)
- Answer
- \(\displaystyle∫(x+1)^4\,dx = \frac{1}{5}(x+1)^5+C\)
9) \(\displaystyle∫(x−1)^5\,dx;\quad u=x−1\)
10) \(\displaystyle∫(2x−3)^{−7}\,dx;\quad u=2x−3\)
- Answer
- \(\displaystyle∫(2x−3)^{−7}\,dx = −\frac{1}{12(2x−3)^6}+C\)
11) \(\displaystyle∫(3x−2)^{−11}\,dx;\quad u=3x−2\)
12) \(\displaystyle∫\frac{x}{\sqrt{x^2+1}}\,dx;\quad u=x^2+1\)
- Answer
- \(\displaystyle∫\frac{x}{\sqrt{x^2+1}}\,dx = \sqrt{x^2+1}+C\)
13) \(\displaystyle∫\frac{x}{\sqrt{1−x^2}}\,dx;\quad u=1−x^2\)
14) \(\displaystyle∫(x−1)(x^2−2x)^3\,dx;\quad u=x^2−2x\)
- Answer
- \(\displaystyle∫(x−1)(x^2−2x)^3\,dx = \frac{1}{8}(x^2−2x)^4+C\)
15) \(\displaystyle∫(x^2−2x)(x^3−3x^2)^2\,dx;\quad u=x^3=3x^2\)
16) \(\displaystyle∫\cos^3 θ\,dθ;\quad u=\sin θ\) (Hint: \(\cos^2 θ=1−\sin^2 θ\))
- Answer
- \(\displaystyle∫\cos^3 θ\,dθ = \sin θ−\dfrac{\sin^3 θ}{3}+C\)
17) \(\displaystyle ∫\sin^3 θ\,dθ;\quad u=\cos θ\) (Hint: \(\sin^2 θ=1−\cos^2θ\))
In exercises 18 - 34, use a suitable change of variables to determine the indefinite integral.
18) \(\displaystyle∫x(1−x)^{99}\,dx\)
- Answer
- \(\begin{align*} \displaystyle∫x(1−x)^{99}\,dx &= \frac{(1−x)^{101}}{101}−\frac{(1−x)^{100}}{100}+C \\[4pt]
&=-\frac{(1-x)^{100}}{10100}\big[ 100x + 1 \big]+C \end{align*}\)
19) \(\displaystyle∫t(1−t^2)^{10}dt\)
20) \(\displaystyle∫(11x−7)^{−3}\,dx\)
- Answer
- \(\displaystyle∫(11x−7)^{−3}\,dx = −\frac{1}{22(11x−7)^2}+C\)
21) \(\displaystyle∫(7x−11)^4\,dx\)
22) \(\displaystyle∫\cos^3 θ\sin θ\,dθ\)
- Answer
- \(\displaystyle∫\cos^3 θ\sin θ\,dθ = −\frac{\cos^4 θ}{4}+C\)
23) \(\displaystyle∫\sin^7 θ\cos θ\,dθ\)
24) \(\displaystyle∫\cos^2(πt)\sin(πt)\,dt\)
- Answer
- \(\displaystyle∫\cos^2(πt)\sin(πt)\,dt = −\frac{cos^3(πt)}{3π}+C\)
25) \(\displaystyle∫\sin^2 x\cos^3 x\,dx\) (Hint: \(\sin^2 x+\cos^2 x=1\))
26) \(\displaystyle∫t\sin(t^2)\cos(t^2)\,dt\)
- Answer
- \(\displaystyle∫t\sin(t^2)\cos(t^2)\,dt = −\frac{1}{4}\cos^2(t^2)+C\)
27) \(\displaystyle∫t^2\cos^2(t^3)\sin(t^3)\,dt\)
28) \(\displaystyle∫\frac{x^2}{(x^3−3)^2}\,dx\)
- Answer
- \(\displaystyle∫\frac{x^2}{(x^3−3)^2}\,dx = −\frac{1}{3(x^3−3)}+C\)
29) \(\displaystyle∫\frac{x^3}{\sqrt{1−x^2}}\,dx\)
30) \(\displaystyle∫\frac{y^5}{(1−y^3)^{3/2}}\,dy\)
- Answer
- \(\displaystyle∫\frac{y^5}{(1−y^3)^{3/2}}\,dy = −\frac{2(y^3−2)}{3\sqrt{1−y^3}}+C\)
31) \(\displaystyle∫\cos θ(1−\cos θ)^{99}\sin θ\,dθ\)
32) \(\displaystyle∫(1−\cos^3 θ)^{10}\cos^2 θ\sin θ\,dθ\)
- Answer
- \(\displaystyle∫(1−\cos^3 θ)^{10}\cos^2 θ\sin θ\,dθ = \frac{1}{33}(1−\cos^3 θ)^{11}+C\)
33) \(\displaystyle∫(\cos θ−1)(\cos^2 θ−2\cos θ)^3\sin θ\,dθ\)
34) \(\displaystyle∫(\sin^2 θ−2\sin θ)(\sin^3 θ−3\sin^2 θ)^3\cos θ\,dθ\)
- Answer
- \(\displaystyle∫(\sin^2 θ−2\sin θ)(\sin^3 θ−3\sin^2 θ)^3\cos θ\,dθ = \frac{1}{12}(\sin^3 θ−3\sin^2 θ)^4+C\)
In exercises 35 - 38, use a calculator to estimate the area under the curve using left Riemann sums with 50 terms, then use substitution to solve for the exact answer.
35) [T] \(y=3(1−x)^2\) over \([0,2]\)
36) [T] \(y=x(1−x^2)^3\) over \([−1,2]\)
- Answer
- \(L_{50}=−8.5779.\) The exact area is \(\frac{−81}{8}\) units\(^2\).
37) [T] \(y=\sin x(1−\cos x)^2\) over \([0,π]\)
38) [T] \(y=\dfrac{x}{(x^2+1)^2}\) over \([−1,1]\)
- Answer
- \(L_{50}=−0.006399\). The exact area is 0.
In exercises 39 - 44, use a change of variables to evaluate the definite integral.
39) \(\displaystyle∫^1_0x\sqrt{1−x^2}\,dx\)
40) \(\displaystyle∫^1_0\frac{x}{\sqrt{1+x^2}}\,dx\)
- Answer
- \(\displaystyle u=1+x^2,\quad du=2x\,dx,\quad ∫^1_0\frac{x}{\sqrt{1+x^2}}\,dx = \frac{1}{2}∫^2_1u^{−1/2}du=\sqrt{2}−1\)
41) \(\displaystyle∫^2_0\frac{t}{\sqrt{5+t^2}}\,dt\)
42) \(\displaystyle∫^1_0\frac{t^2}{\sqrt{1+t^3}}\,dt\)
- Answer
- \(\displaystyle u=1+t^3,\quad du=3t^2,\quad ∫^1_0\frac{t^2}{\sqrt{1+t^3}}\,dt = \frac{1}{3}∫^2_1u^{−1/2}du=\frac{2}{3}(\sqrt{2}−1)\)
43) \(\displaystyle∫^{π/4}_0\sec^2 θ\tan θ\,dθ\)
44) \(\displaystyle∫^{π/4}_0\frac{\sin θ}{\cos^4 θ}\,dθ\)
- Answer
- \(\displaystyle u=\cos θ,\quad du=−\sin θ\,dθ,\quad \int^{π/4}_0\frac{\sin θ}{\cos^4 θ}\,dθ = -∫_1^{\sqrt{2}/2}u^{−4}\,du = ∫^1_{\sqrt{2}/2}u^{−4}\,du=\frac{1}{3}(2\sqrt{2}−1)\)
In exercises 45 - 50, evaluate the indefinite integral \(\displaystyle ∫f(x)\,dx\) with constant \(C=0\) using \(u\)-substitution. Then, graph the function and the antiderivative over the indicated interval. If possible, estimate a value of \(C\) that would need to be added to the antiderivative to make it equal to the definite integral \(\displaystyle F(x)=∫^x_af(t)\,dt\), with a the left endpoint of the given interval.
45) [T] \(\displaystyle∫(2x+1)e^{x^2+x−6}\,dx\) over \([−3,2]\)
46) [T] \(\displaystyle∫\frac{\cos(\ln(2x))}{x}\,dx\) on \([0,2]\)
- Answer
-
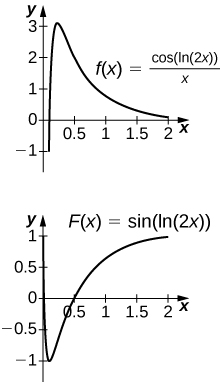
The antiderivative is \(y=\sin(\ln(2x))\). Since the antiderivative is not continuous at \(x=0\), one cannot find a value of C that would make \(y=\sin(\ln(2x))−C\) work as a definite integral.
47) [T] \(\displaystyle ∫\frac{3x^2+2x+1}{\sqrt{x^3+x^2+x+4}}\,dx\) over \([−1,2]\)
48) [T] \(\displaystyle ∫\frac{\sin x}{\cos^3x}\,dx\) over \(\left[−\frac{π}{3},\frac{π}{3}\right]\)
- Answer
-
![Two graphs. The first is the function f(x) = sin(x) / cos(x)^3 over [-5pi/16, 5pi/16]. It is an increasing concave down function for values less than zero and an increasing concave up function for values greater than zero. The second is the fuction f(x) = ½ sec(x)^2 over the same interval. It is a wide, concave up curve which decreases for values less than zero and increases for values greater than zero.](https://math.libretexts.org/@api/deki/files/2632/CNX_Calc_Figure_05_05_206.jpeg?revision=1&size=bestfit&width=353&height=786)
The antiderivative is \(y=\frac{1}{2}\sec^2 x\). You should take \(C=−2\) so that \(F(−\frac{π}{3})=0.\)
49) [T] \(\displaystyle ∫(x+2)e^{−x^2−4x+3}\,dx\) over \([−5,1]\)
50) [T] \(\displaystyle ∫3x^2\sqrt{2x^3+1}\,dx\) over \([0,1]\)
- Answer
-
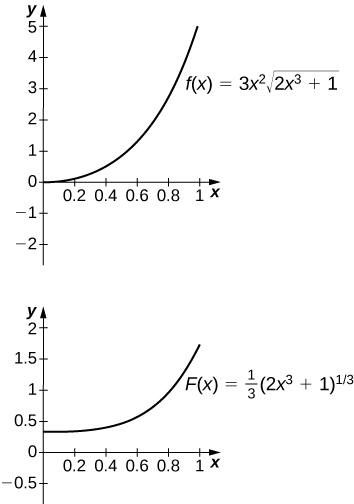
The antiderivative is \( y=\frac{1}{3}(2x^3+1)^{3/2}\). One should take \(C=−\frac{1}{3}\).
51) If \(h(a)=h(b)\) in \(\displaystyle ∫^b_ag'(h(x))h(x)\,dx,\) what can you say about the value of the integral?
52) Is the substitution \(u=1−x^2\) in the definite integral \(\displaystyle ∫^2_0\frac{x}{1−x^2}\,dx\) okay? If not, why not?
- Answer
- No, because the integrand is discontinuous at \(x=1\).
In exercises 53 - 59, use a change of variables to show that each definite integral is equal to zero.
53) \(\displaystyle ∫^π_0\cos^2(2θ)\sin(2θ)\,dθ\)
54) \(\displaystyle ∫^\sqrt{π}_0t\cos(t^2)\sin(t^2)\,dt\)
- Answer
- \(u=\sin(t^2);\) the integral becomes \(\displaystyle \frac{1}{2}∫^0_0u\,du.\)
55) \(\displaystyle ∫^1_0(1−2t)\,dt\)
56) \(\displaystyle ∫^1_0\frac{1−2t}{1+(t−\frac{1}{2})^2}\,dt\)
- Answer
- \(u=1+(t−\frac{1}{2})^2;\) the integral becomes \(\displaystyle −∫^{5/4}_{5/4}\frac{1}{u}\,du\).
57) \(\displaystyle ∫^π_0\sin\left(\left(t−\tfrac{π}{2}\right)^3\right)\cos\left(t−\tfrac{π}{2}\right)\,dt\)
58) \(\displaystyle ∫^2_0(1−t)\cos(πt)\,dt\)
- Answer
- \(u=1−t;\) Since the integrand is odd, the integral becomes
\[∫^{−1}_1u\cos\big(π(1−u)\big)\,du=∫^{−1}_1u[\cos π\cos u−\sin π\sin u]\,du=−∫^{−1}_1u\cos u\,du=∫_{-1}^1u\cos u\,du=0\nonumber \]
59) \(\displaystyle ∫^{3π/4}_{π/4}\sin^2 t\cos t\,dt\)
60) Show that the average value of \(f(x)\) over an interval \([a,b]\) is the same as the average value of \(f(cx)\) over the interval \(\left[\frac{a}{c},\frac{b}{c}\right]\) for \(c>0.\)
- Answer
- Setting \(u=cx\) and \(du=c\,dx\) gets you \(\displaystyle \frac{1}{\frac{b}{c}−\frac{a}{c}}∫^{b/c}_{a/c}f(cx)\,dx=\frac{c}{b−a}∫^{u=b}_{u=a}f(u)\frac{du}{c}=\frac{1}{b−a}∫^b_af(u)\,du.\)
61) Find the area under the graph of \(f(t)=\dfrac{t}{(1+t^2)^a}\) between \(t=0\) and \(t=x\) where \(a>0\) and \(a≠1\) is fixed, and evaluate the limit as \(x→∞\).
62) Find the area under the graph of \(g(t)=\dfrac{t}{(1−t^2)^a}\) between \(t=0\) and \(t=x\), where \(0<x<1\) and \(a>0\) is fixed. Evaluate the limit as \(x→1\).
- Answer
- \(\displaystyle ∫^x_0g(t)\,dt=\frac{1}{2}∫^1_{u=1−x^2} \frac{du}{u^a}=\frac{1}{2(1−a)}u^{1−a}∣1u=\frac{1}{2(1−a)}(1−(1−x^2)^{1−a})\) As \(x→1\) the limit is \(\dfrac{1}{2(1−a)}\) if \(a<1\), and the limit diverges to \(+∞\) if \(a>1\).
63) The area of a semicircle of radius \(1\) can be expressed as \(\displaystyle ∫^1_{−1}\sqrt{1−x^2}\,dx\). Use the substitution \(x=\cos t\) to express the area of a semicircle as the integral of a trigonometric function. You do not need to compute the integral.
64) The area of the top half of an ellipse with a major axis that is the \(x\)-axis from \(x=−1\) to a and with a minor axis that is the \(y\)-axis from \(y=−b\) to \(y=b\) can be written as \(\displaystyle ∫^a_{−a}b\sqrt{1−\frac{x^2}{a^2}}\,dx\). Use the substitution \(x=a\cos t\) to express this area in terms of an integral of a trigonometric function. You do not need to compute the integral.
- Answer
- \(\displaystyle ∫^{t=0}_{t=π}b\sqrt{1−\cos^2 t}×(−a\sin t)\,dt=∫^{t=π}_{t=0}ab\sin^2 t\,dt\)
65) [T] The following graph is of a function of the form \( f(t)=a\sin(nt)+b\sin(mt)\). Estimate the coefficients \(a\) and \(b\) and the frequency parameters \(n\) and \(m\). Use these estimates to approximate \(\displaystyle ∫^π_0f(t)\,dt\).
![A graph of a function of the given form over [0, 2pi], which has six turning points. They are located at just before pi/4, just after pi/2, between 3pi/4 and pi, between pi and 5pi/4, just before 3pi/2, and just after 7pi/4 at about 3, -2, 1, -1, 2, and -3. It begins at the origin and ends at (2pi, 0). It crosses the x axis between pi/4 and pi/2, just before 3pi/4, pi, just after 5pi/4, and between 3pi/2 and 4pi/4.](https://math.libretexts.org/@api/deki/files/2634/CNX_Calc_Figure_05_05_201.jpeg?revision=1&size=bestfit&width=325&height=246)
66) [T] The following graph is of a function of the form \(f(x)=a\cos(nt)+b\cos(mt)\). Estimate the coefficients \(a\) and \(b\) and the frequency parameters \(n\) and \(m\). Use these estimates to approximate \(\displaystyle ∫^π_0f(t)\,dt.\)
![The graph of a function of the given form over [0, 2pi]. It begins at (0,1) and ends at (2pi, 1). It has five turning points, located just after pi/4, between pi/2 and 3pi/4, pi, between 5pi/4 and 3pi/2, and just before 7pi/4 at about -1.5, 2.5, -3, 2.5, and -1. It crosses the x axis between 0 and pi/4, just before pi/2, just after 3pi/4, just before 5pi/4, just after 3pi/2, and between 7pi/4 and 2pi.](https://math.libretexts.org/@api/deki/files/2635/CNX_Calc_Figure_05_05_202.jpeg?revision=1&size=bestfit&width=325&height=246)
- Answer
- \(f(t)=2\cos(3t)−\cos(2t);\quad \displaystyle ∫^{π/2}_0(2\cos(3t)−\cos(2t))\,dt=−\frac{2}{3}\)

