Chapter 7 Review Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
selected template will load here
This action is not available.
( \newcommand{\kernel}{\mathrm{null}\,}\)
In exercises 1 - 4, determine whether the statement is true or false. Justify your answer with a proof or a counterexample.
1) ∫exsin(x)dx cannot be integrated by parts.
2) ∫1x4+1dx cannot be integrated using partial fractions.
3) In numerical integration, increasing the number of points decreases the error.
4) Integration by parts can always yield the integral.
In exercises 5 - 10, evaluate the integral using the specified method.
5) ∫x2sin(4x)dx, using integration by parts
6) ∫1x2√x2+16dx, using trigonometric substitution
7) ∫√xlnxdx, using integration by parts
8) ∫3xx3+2x2−5x−6dx, using partial fractions
9) ∫x5(4x2+4)5/2dx, using trigonometric substitution
10) ∫√4−sin2(x)sin2(x)cos(x)dx, using a table of integrals or a CAS
In exercises 11 - 15, integrate using whatever method you choose.
11) ∫sin2xcos2xdx
12) ∫x3√x2+2dx
13) ∫3x2+1x4−2x3−x2+2xdx
14) ∫1x4+4dx
15) ∫√3+16x4x4dx
In exercises 16 - 18, approximate the integrals using the midpoint rule, trapezoidal rule, and Simpson’s rule using four subintervals, rounding to three decimals.
16) [T] ∫21√x5+2dx
17) [T] ∫√π0e−sin(x2)dx
18) [T] ∫41ln(1/x)xdx
In exercises 19 - 20, evaluate the integrals, if possible.
19) ∫∞11xndx, for what values of n does this integral converge or diverge?
20) ∫∞1e−xxdx
In exercises 21 - 22, consider the gamma function given by Γ(a)=∫∞0e−yya−1dy.
21) Show that Γ(a)=(a−1)Γ(a−1).
22) Extend to show that Γ(a)=(a−1)!, assuming a is a positive integer.
The fastest car in the world, the Bugati Veyron, can reach a top speed of 408 km/h. The graph represents its velocity.
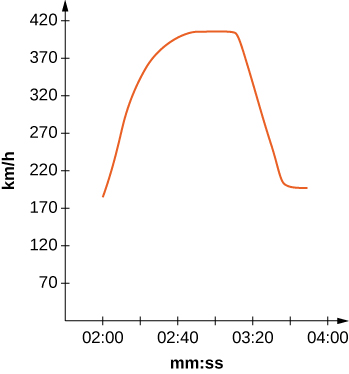
23) [T] Use the graph to estimate the velocity every 20 sec and fit to a graph of the form v(t)=aebxsin(cx)+d. (Hint: Consider the time units.)
24) [T] Using your function from the previous problem, find exactly how far the Bugati Veyron traveled in the 1 min 40 sec included in the graph.

