Chapter 8 Review Exercises
- Last updated
- Jun 30, 2021
- Save as PDF
- Page ID
- 10787
( \newcommand{\kernel}{\mathrm{null}\,}\)
True or False? Justify your answer with a proof or a counterexample.
1) The differential equation y′=3x2y−cos(x)y″ is linear.
2) The differential equation y′=x−y is separable.
- Answer
- F
3) You can explicitly solve all first-order differential equations by separation or by the method of integrating factors.
4) You can determine the behavior of all first-order differential equations using directional fields or Euler’s method.
- Answer
- T
For the following problems, find the general solution to the differential equations.
5) y′=x2+3ex−2x
6) y′=2x+cos−1x
- Answer
- y(x)=2xln(2)+xcos−1x−√1−x2+C
7) y′=y(x2+1)
8) y′=e−ysinx
- Answer
- y(x)=ln(C−cosx)
9) y′=3x−2y
10) y′=ylny
- Answer
- y(x)=eeC+x
For the following problems, find the solution to the initial value problem.
11) y′=8x−lnx−3x4,y(1)=5
12) y′=3x−cosx+2,y(0)=4
- Answer
- y(x)=4+32x2+2x−sinx
13) xy′=y(x−2),y(1)=3
14) y′=3y2(x+cosx),y(0)=−2
- Answer
- y(x)=−21+3(x2+2sinx)
15) (x−1)y′=y−2,y(0)=0
16) y′=3y−x+6x2,y(0)=−1
- Answer
- y(x)=−2x2−2x−13−23e3x
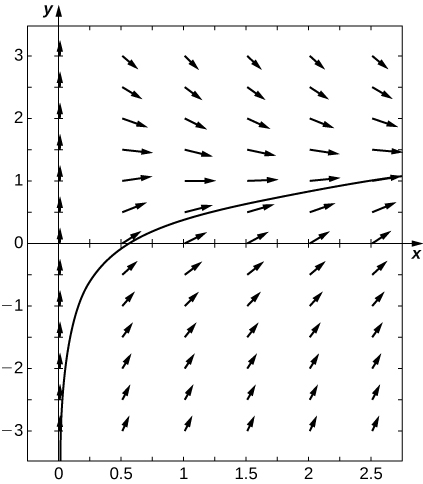
For the following problems, draw the directional field associated with the differential equation, then solve the differential equation. Draw a sample solution on the directional field.
17) y′=2y−y2
18) y′=1x+lnx−y, for x>0
- Answer
-
y(x)=Ce−x+lnx
For the following problems, use Euler’s Method with n=5 steps over the interval t=[0,1]. Then solve the initial-value problem exactly. How close is your Euler’s Method estimate?
19) y′=−4yx,y(0)=1
20) y′=3x−2y,y(0)=0
- Answer
- Euler: 0.6939,
Exact solution: y(x)=3x−e−2x2+ln(3)
For the following problems, set up and solve the differential equations.
21) A car drives along a freeway, accelerating according to a=5\sin(πt), where t represents time in minutes. Find the velocity at any time t, assuming the car starts with an initial speed of 60 mph.
22) You throw a ball of mass 2 kilograms into the air with an upward velocity of 8 m/s. Find exactly the time the ball will remain in the air, assuming that gravity is given by g=9.8\,\text{m/s}^2.
- Answer
- \frac{40}{49} second
23) You drop a ball with a mass of 5 kilograms out an airplane window at a height of 5000 m. How long does it take for the ball to reach the ground?
24) You drop the same ball of mass 5 kilograms out of the same airplane window at the same height, except this time you assume a drag force proportional to the ball’s velocity, using a proportionality constant of 3 and the ball reaches terminal velocity. Solve for the distance fallen as a function of time. How long does it take the ball to reach the ground?
- Answer
- x(t)=5000+\frac{245}{9}−\frac{49}{3}t−\frac{245}{9}e^{−5/3t}, \quad t=307.8 seconds
25) A drug is administered to a patient every 24 hours and is cleared at a rate proportional to the amount of drug left in the body, with proportionality constant 0.2. If the patient needs a baseline level of 5 mg to be in the bloodstream at all times, how large should the dose be?
26) A 1000-liter tank contains pure water and a solution of 0.2 kg salt/L is pumped into the tank at a rate of 1 L/min and is drained at the same rate. Solve for total amount of salt in the tank at time t.
- Answer
- T(t)=200\left(1−e^{−t/1000}\right)
27) You boil water to make tea. When you pour the water into your teapot, the temperature is 100°C. After 5 minutes in your 15°C room, the temperature of the tea is 85°C. Solve the equation to determine the temperatures of the tea at time t. How long must you wait until the tea is at a drinkable temperature (72°C)?
28) The human population (in thousands) of Nevada in 1950 was roughly 160. If the carrying capacity is estimated at 10 million individuals, and assuming a growth rate of 2\% per year, develop a logistic growth model and solve for the population in Nevada at any time (use 1950 as time = 0). What population does your model predict for 2000? How close is your prediction to the true value of 1,998,257?
- Answer
- P(t)=\dfrac{1600000e^{0.02t}}{9840+160e^{0.02t}}
29) Repeat the previous problem but use Gompertz growth model. Which is more accurate?


