9.2: Infinite Series
- Last updated
- Oct 18, 2018
- Save as PDF
- Page ID
- 10791
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Explain the meaning of the sum of an infinite series.
- Calculate the sum of a geometric series.
- Evaluate a telescoping series.
We have seen that a sequence is an ordered set of terms. If you add these terms together, you get a series. In this section we define an infinite series and show how series are related to sequences. We also define what it means for a series to converge or diverge. We introduce one of the most important types of series: the geometric series. We will use geometric series in the next chapter to write certain functions as polynomials with an infinite number of terms. This process is important because it allows us to evaluate, differentiate, and integrate complicated functions by using polynomials that are easier to handle. We also discuss the harmonic series, arguably the most interesting divergent series because it just fails to converge.
Sums and Series
An infinite series is a sum of infinitely many terms and is written in the form
∞∑n=1an=a1+a2+a3+⋯.
But what does this mean? We cannot add an infinite number of terms in the same way we can add a finite number of terms. Instead, the value of an infinite series is defined in terms of the limit of partial sums. A partial sum of an infinite series is a finite sum of the form
k∑n=1an=a1+a2+a3+⋯+ak.
To see how we use partial sums to evaluate infinite series, consider the following example. Suppose oil is seeping into a lake such that 1000 gallons enters the lake the first week. During the second week, an additional 500 gallons of oil enters the lake. The third week, 250 more gallons enters the lake. Assume this pattern continues such that each week half as much oil enters the lake as did the previous week. If this continues forever, what can we say about the amount of oil in the lake? Will the amount of oil continue to get arbitrarily large, or is it possible that it approaches some finite amount? To answer this question, we look at the amount of oil in the lake after k weeks. Letting Sk denote the amount of oil in the lake (measured in thousands of gallons) after k weeks, we see that
S1=1
S2=1+0.5=1+12
S3=1+0.5+0.25=1+12+14
S4=1+0.5+0.25+0.125=1+12+14+18
S5=1+0.5+0.25+0.125+0.0625=1+12+14+18+116.
Looking at this pattern, we see that the amount of oil in the lake (in thousands of gallons) after k weeks is
Sk=1+12+14+18+116+⋯+12k−1=k∑n=1(12)n−1.
We are interested in what happens as k→∞. Symbolically, the amount of oil in the lake as k→∞ is given by the infinite series
∞∑n=1(12)n−1=1+12+14+18+116+⋯.
At the same time, as k→∞, the amount of oil in the lake can be calculated by evaluating limk→∞Sk. Therefore, the behavior of the infinite series can be determined by looking at the behavior of the sequence of partial sums Sk. If the sequence of partial sums Sk converges, we say that the infinite series converges, and its sum is given by limk→∞Sk. If the sequence Sk diverges, we say the infinite series diverges. We now turn our attention to determining the limit of this sequence Sk.
First, simplifying some of these partial sums, we see that
S1=1
S2=1+12=32
S3=1+12+14=74
S4=1+12+14+18=158
S_5=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=\frac{31}{16}.
Plotting some of these values in Figure \PageIndex{1}, it appears that the sequence {S_k} could be approaching 2.
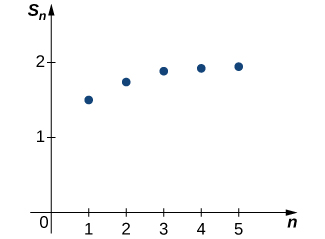
Let’s look for more convincing evidence. In the following table, we list the values of S_k for several values of k.
| k | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| S_k | 1.9375 | 1.998 | 1.999939 | 1.999998 |
These data supply more evidence suggesting that the sequence {S_k} converges to 2. Later we will provide an analytic argument that can be used to prove that \displaystyle \lim_{k→∞}S_k=2. For now, we rely on the numerical and graphical data to convince ourselves that the sequence of partial sums does actually converge to 2. Since this sequence of partial sums converges to 2, we say the infinite series converges to 2 and write
\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=2.\nonumber
Returning to the question about the oil in the lake, since this infinite series converges to 2, we conclude that the amount of oil in the lake will get arbitrarily close to 2000 gallons as the amount of time gets sufficiently large.
This series is an example of a geometric series. We discuss geometric series in more detail later in this section. First, we summarize what it means for an infinite series to converge.
Definition
An infinite series is an expression of the form
\sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯. \nonumber
For each positive integer k, the sum
S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k \nonumber
is called the k^{\text{th}} partial sum of the infinite series. The partial sums form a sequence {S_k}. If the sequence of partial sums converges to a real number S, the infinite series converges. If we can describe the convergence of a series to S, we call S the sum of the series, and we write
\sum_{n=1}^∞a_n=S. \nonumber
If the sequence of partial sums diverges, we have the divergence of a series.
Note that the index for a series need not begin with n=1 but can begin with any value. For example, the series
\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1} \nonumber
can also be written as
\sum_{n=0}^∞\left(\frac{1}{2}\right)^n\; \text{or}\; \sum_{n=5}^∞\left(\frac{1}{2}\right)^{n−5}. \nonumber
Often it is convenient for the index to begin at 1, so if for some reason it begins at a different value, we can re-index by making a change of variables. For example, consider the series
\sum_{n=2}^∞\frac{1}{n^2}. \nonumber
By introducing the variable m=n−1, so that n=m+1, we can rewrite the series as
\sum_{m=1}^∞\frac{1}{(m+1)^2}. \nonumber
Example \PageIndex{1}: Evaluating Limits of Sequences of Partial Sums
For each of the following series, use the sequence of partial sums to determine whether the series converges or diverges.
- \displaystyle \sum_{n=1}^∞\frac{n}{n+1}
- \displaystyle \sum_{n=1}^∞(−1)^n
- \displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}
Solution
a. The sequence of partial sums {S_k} satisfies
S_1=\dfrac{1}{2}
S_2=\dfrac{1}{2}+\dfrac{2}{3}
S_3=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}
S_4=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}.
Notice that each term added is greater than 1/2. As a result, we see that
S_1=\dfrac{1}{2}
S_2=\dfrac{1}{2}+\dfrac{2}{3}>\dfrac{1}{2}+\dfrac{1}{2}=2\left(\dfrac{1}{2}\right)
S_3=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=3\left(\dfrac{1}{2}\right)
S_4=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=4\left(\dfrac{1}{2}\right).
From this pattern we can see that S_k>k\left(\frac{1}{2}\right) for every integer k. Therefore, {S_k} is unbounded and consequently, diverges. Therefore, the infinite series \displaystyle \sum^∞_{n=1}\frac{n}{n+1} diverges.
b. The sequence of partial sums {S_k} satisfies
S_1=−1
S_2=−1+1=0
S_3=−1+1−1=−1
S_4=−1+1−1+1=0.
From this pattern we can see the sequence of partial sums is
{S_k}={−1,0,−1,0,…}. \nonumber
Since this sequence diverges, the infinite series \displaystyle \sum^∞_{n=1}(−1)^n diverges.
c. The sequence of partial sums {S_k} satisfies
S_1=\dfrac{1}{1⋅2}=\dfrac{1}{2}
S_2=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}=\dfrac{1}{2}+\dfrac{1}{6}=\dfrac{2}{3}
S_3=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}=\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}=\dfrac{3}{4}
S_4=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}+\dfrac{1}{4⋅5}=\dfrac{4}{5}
S_5=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}+\dfrac{1}{4⋅5}+\dfrac{1}{5⋅6}=\dfrac{5}{6}.
From this pattern, we can see that the k^{\text{th}} partial sum is given by the explicit formula
S_k=\frac{k}{k+1} \nonumber .
Since k/(k+1)→1, we conclude that the sequence of partial sums converges, and therefore the infinite series converges to 1. We have
\sum_{n=1}^∞\frac{1}{n(n+1)}=1. \nonumber
Exercise \PageIndex{1}
Determine whether the series \displaystyle \sum^∞_{n=1}\frac{n+1}{n} converges or diverges.
- Hint
-
Look at the sequence of partial sums.
- Answer
-
The series diverges because the k^{\text{th}} partial sum S_k>k.
The Harmonic Series
A useful series to know about is the harmonic series. The harmonic series is defined as
\sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯. \nonumber
This series is interesting because it diverges, but it diverges very slowly. By this we mean that the terms in the sequence of partial sums {S_k} approach infinity, but do so very slowly. We will show that the series diverges, but first we illustrate the slow growth of the terms in the sequence {S_k} in the following table.
| k | 10 | 100 | 1000 | 10,00 | 100,000 | 1,000,000 |
|---|---|---|---|---|---|---|
| S_k | 2.92897 | 5.18738 | 7.48547 | 9.78761 | 12.09015 | 14.39273 |
Even after 1,000,000 terms, the partial sum is still relatively small. From this table, it is not clear that this series actually diverges. However, we can show analytically that the sequence of partial sums diverges, and therefore the series diverges.
To show that the sequence of partial sums diverges, we show that the sequence of partial sums is unbounded. We begin by writing the first several partial sums:
S_1=1
S_2=1+\dfrac{1}{2}
S_3=1+\dfrac{1}{2}+\dfrac{1}{3}
S_4=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}.
Notice that for the last two terms in S_4,
\frac{1}{3}+\frac{1}{4}>\frac{1}{4}+\frac{1}{4} \nonumber
Therefore, we conclude that
S_4>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)=1+\frac{1}{2}+\frac{1}{2}=1+2\left(\frac{1}{2}\right). \nonumber
Using the same idea for S_8, we see that
\displaystyle S_8=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right)=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=1+3\left(\frac{1}{2}\right).
From this pattern, we see that S_1=1, S_2=1+1/2, S_4>1+2(1/2), and S_8>1+3(1/2). More generally, it can be shown that S_{2^j}>1+j(1/2) for all j>1. Since 1+j(1/2)→∞, we conclude that the sequence {S_k} is unbounded and therefore diverges. In the previous section, we stated that convergent sequences are bounded. Consequently, since {S_k} is unbounded, it diverges. Thus, the harmonic series diverges.
Algebraic Properties of Convergent Series
Since the sum of a convergent infinite series is defined as a limit of a sequence, the algebraic properties for series listed below follow directly from the algebraic properties for sequences.
Note \PageIndex{1}: Algebraic Properties of Convergent Series
Let \displaystyle \sum_{n=1}^∞ a_n and \displaystyle \sum_{n=1}^∞ b_n be convergent series. Then the following algebraic properties hold.
i. The series \displaystyle \sum_{n=1}^∞(a_n+b_n) converges, and \displaystyle \sum^∞_{n=1}(a_n+b_n)=\sum^∞_{n=1}a_n+\sum^∞_{n=1}b_n. (Sum Rule)
ii. The series \displaystyle \sum_{n=1}^∞(a_n−b_n) converges, and \displaystyle \sum^∞_{n=1}(a_n−b_n)=\sum^∞_{n=1}a_n−\sum^∞_{n=1}b_n. (Difference Rule)
iii. For any real number c, the series \displaystyle \sum_{n=1}^∞ca_n converges, and \displaystyle \sum^∞_{n=1}ca_n=c\sum^∞_{n=1}a_n. (Constant Multiple Rule)
Example \PageIndex{2}: Using Algebraic Properties of Convergent Series
Evaluate \displaystyle \sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right].
Solution
We showed earlier that
\sum_{n=1}^∞\frac{1}{n(n+1)} = 1 \nonumber
and
\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=2. \nonumber
Since both of those series converge, we can apply the properties of Note \PageIndex{1} to evaluate
\sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right]. \nonumber
Using the sum rule, write
\displaystyle \sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right]=\sum_{n=1}^∞\frac{3}{n(n+1)}+\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−2}.
Then, using the constant multiple rule and the sums above, we can conclude that
\displaystyle \sum^∞_{n=1}\frac{3}{n(n+1)}+\sum^∞_{n=1}\left(\frac{1}{2}\right)^{n−2}=3\sum^∞_{n=1}\frac{1}{n(n+1)}+\left(\frac{1}{2}\right)^{−1}\sum^∞_{n=1}\left(\frac{1}{2}\right)^{n−1}=3(1)+\left(\frac{1}{2}\right)^{−1}(2)=3+2(2)=7.
Exercise \PageIndex{2}
Evaluate \displaystyle \sum^∞_{n=1}\frac{5}{2^{n−1}}.
- Hint
-
Rewrite as \displaystyle \sum^∞_{n=1}5\left(\frac{1}{2}\right)^{n−1}.
- Answer
-
10
Geometric Series
A geometric series is any series that we can write in the form
a+ar+ar^2+ar^3+⋯=\sum_{n=1}^∞ar^{n−1}. \nonumber
Because the ratio of each term in this series to the previous term is r, the number r is called the ratio. We refer to a as the initial term because it is the first term in the series. For example, the series
\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+⋯ \nonumber
is a geometric series with initial term a=1 and ratio r=1/2.
In general, when does a geometric series converge? Consider the geometric series
\sum_{n=1}^∞ar^{n−1} \nonumber
when a>0. Its sequence of partial sums {S_k} is given by
S_k=\sum_{n=1}^kar^{n−1}=a+ar+ar^2+⋯+ar^{k−1}. \nonumber
Consider the case when r=1. In that case,
S_k=a+a(1)+a(1)^2+⋯+a(1)^{k−1}=ak. \nonumber
Since a>0, we know ak→∞ as k→∞. Therefore, the sequence of partial sums is unbounded and thus diverges. Consequently, the infinite series diverges for r=1. For r≠1, to find the limit of {S_k}, multiply Equation by 1−r. Doing so, we see that
(1−r)S_k=a(1−r)(1+r+r^2+r^3+⋯+r^{k−1})=a[(1+r+r^2+r^3+⋯+r^{k−1})−(r+r^2+r^3+⋯+r^k)]=a(1−r^k). \nonumber
All the other terms cancel out.
Therefore,
S_k=\dfrac{a(1−r^k)}{1−r} for r≠1.
From our discussion in the previous section, we know that the geometric sequence r^k→0 if |r|<1 and that r^k diverges if |r|>1 or r=±1. Therefore, for |r|<1, S_k→\dfrac{a}{1−r} and we have
\sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\; \text{if}\; |r|<1. \nonumber
If |r|≥1, \, S_k diverges, and therefore
\sum_{n=1}^∞ar^{n−1} \; \text{diverges if}\; |r|≥1. \nonumber
Definitions: Diverging and Converging Series
A geometric series is a series of the form
\sum_{n=1}^∞ar^{n−1}=a+ar+ar^2+ar^3+⋯. \label{geoseriesdef}
If |r|<1, the series converges, and
\sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\; \text{for}\; |r|<1. \nonumber
If |r|≥1, the series diverges.
Geometric series sometimes appear in slightly different forms. For example, sometimes the index begins at a value other than n=1 or the exponent involves a linear expression for n other than n−1. As long as we can rewrite the series in the form given by Equation \ref{geoseriesdef}, it is a geometric series. For example, consider the series
\sum_{n=0}^∞\left(\frac{2}{3}\right)^{n+2}. \nonumber
To see that this is a geometric series, we write out the first several terms:
\displaystyle \sum_{n=0}^∞\left(\frac{2}{3}\right)^{n+2}=\left(\frac{2}{3}\right)^2+\left(\frac{2}{3}\right)^3+\left(\frac{2}{3}\right)^4+⋯=\frac{4}{9}+\frac{4}{9}⋅\left(\frac{2}{3}\right)+\frac{4}{9}⋅\left(\frac{2}{3}\right)^2+⋯.
We see that the initial term is a=4/9 and the ratio is r=2/3. Therefore, the series can be written as
\displaystyle \sum_{n=1}^∞\frac{4}{9}⋅\left(\frac{2}{3}\right)^{n−1}.
Since r=2/3<1, this series converges, and its sum is given by
\displaystyle \sum_{n=1}^∞\frac{4}{9}⋅\left(\frac{2}{3}\right)^{n−1}=\frac{4/9}{1−2/3}=\frac{4}{3}.
Example \PageIndex{3}: Determining Convergence or Divergence of a Geometric Series
Determine whether each of the following geometric series converges or diverges, and if it converges, find its sum.
- \displaystyle \sum^∞_{n=1}\frac{(−3)^{n+1}}{4^{n−1}}
- \displaystyle \sum^∞_{n=1}e^{2n}
Solution
a. Writing out the first several terms in the series, we have
\begin{align*} \sum_{n=1}^∞\frac{(−3)^{n+1}}{4^{n−1}} &= \frac{(−3)^2}{4^0}+\frac{(−3)^3}{4}+\frac{(−3)^4}{4^2}+⋯ \\[4pt] &=(−3)^2+(−3)^2⋅\left(\frac{−3}{4}\right)+(−3)^2⋅\left(\frac{−3}{4}\right)^2+⋯ \\[4pt] &=9+9⋅\left(\frac{−3}{4}\right)+9⋅\left(\frac{−3}{4}\right)^2+⋯. \end{align*}
The initial term a=−3 and the ratio r=−3/4. Since |r|=3/4<1, the series converges to
\frac{9}{1−(−3/4)}=\frac{9}{7/4}=\frac{36}{7}. \nonumber
b. Writing this series as
e^2\sum_{n=1}^∞(e^2)^{n−1} \nonumber
we can see that this is a geometric series where r=e^2>1. Therefore, the series diverges.
Exercise \PageIndex{3}
Determine whether the series \displaystyle \sum_{n=1}^∞\left(\frac{−2}{5}\right)^{n−1} converges or diverges. If it converges, find its sum.
- Hint
-
r=−2/5
- Answer
-
5/7
We now turn our attention to a nice application of geometric series. We show how they can be used to write repeating decimals as fractions of integers.
Example \PageIndex{4}: Writing Repeating Decimals as Fractions of Integers
Use a geometric series to write 3.\bar{26} as a fraction of integers.
Solution
Since 3.\bar{26}—=3.262626…, first we write
\begin{align*} 3.262626… &= 3+\frac{26}{100}+\frac{26}{10,000}+\frac{26}{100,000}+⋯ \\[4pt] &=3+\frac{26}{10^2}+\frac{26}{10^4}+\frac{26}{10^6}+⋯. \end{align*}
Ignoring the term 3, the rest of this expression is a geometric series with initial term a=26/10^2 and ratio r=1/10^2. Therefore, the sum of this series is
\frac{26/10^2}{1−(1/10^2)}=\frac{26/10^2}{99/10^2}=\frac{26}{99}. \nonumber
Thus,
3.262626…=3+\frac{26}{99}=\frac{323}{99}.
Exercise \PageIndex{4}
Write 5.2\bar{7} as a fraction of integers.
- Hint
-
By expressing this number as a series, find a geometric series with initial term a=7/100 and ratio r=1/10.
- Answer
-
475/90
Example \PageIndex{5}: Finding the Area of the Koch Snowflake
Define a sequence of figures \{F_n\} recursively as follows (Figure \PageIndex{2}). Let F_0 be an equilateral triangle with sides of length 1. For n≥1, let F_n be the curve created by removing the middle third of each side of F_{n−1} and replacing it with an equilateral triangle pointing outward. The limiting figure as n→∞ is known as Koch’s snowflake.
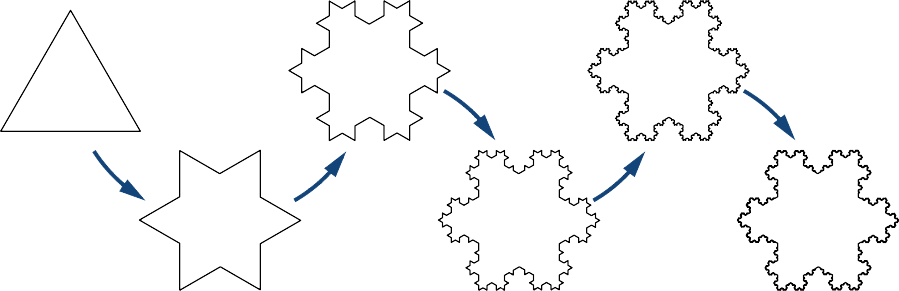
- Find the length L_n of the perimeter of F_n. Evaluate \displaystyle \lim_{n→∞}L_n to find the length of the perimeter of Koch’s snowflake.
- Find the area A_n of figure F_n. Evaluate \displaystyle \lim_{n→∞}A_n to find the area of Koch’s snowflake.
Solution
a. Let N_n denote the number of sides of figure F_n. Since F_0 is a triangle, N_0=3. Let l_n denote the length of each side of F_n. Since F_0 is an equilateral triangle with sides of length l_0=1, we now need to determine N_1 and l_1. Since F_1 is created by removing the middle third of each side and replacing that line segment with two line segments, for each side of F_0, we get four sides in F_1. Therefore, the number of sides for F_1 is
N_1=4⋅3.
Since the length of each of these new line segments is 1/3 the length of the line segments in F_0, the length of the line segments for F_1 is given by
l_1=\frac{1}{3}⋅1=\frac{1}{3}.
Similarly, for F_2, since the middle third of each side of F_1 is removed and replaced with two line segments, the number of sides in F_2 is given by
N_2=4N_1=4(4⋅3)=4^2⋅3.
Since the length of each of these sides is 1/3 the length of the sides of F_1, the length of each side of figure F_2 is given by
l_2=\frac{1}{3}⋅l_1=\frac{1}{3}⋅\frac{1}{3}=\left(\frac{1}{3}\right)^2.
More generally, since F_n is created by removing the middle third of each side of F_{n−1} and replacing that line segment with two line segments of length \frac{1}{3}l_{n−1} in the shape of an equilateral triangle, we know that N_n=4N_{n−1} and l_n=\dfrac{l_{n−1}}{3}. Therefore, the number of sides of figure F_n is
N_n=4^n⋅3
and the length of each side is
l_n=\left(\frac{1}{3}\right)^n. \nonumber
Therefore, to calculate the perimeter of F_n, we multiply the number of sides N_n and the length of each side l_n. We conclude that the perimeter of F_n is given by
L_n=N_n⋅l_n=3⋅\left(\frac{4}{3}\right)^n \nonumber
Therefore, the length of the perimeter of Koch’s snowflake is
L=\lim_{n→∞}L_n=∞. \nonumber
b. Let T_n denote the area of each new triangle created when forming F_n. For n=0, T_0 is the area of the original equilateral triangle. Therefore, T_0=A_0=\sqrt{3}/4. For n≥1, since the lengths of the sides of the new triangle are 1/3 the length of the sides of F_{n−1}, we have
T_n=\left(\frac{1}{3}\right)^2⋅T_{n−1}=\frac{1}{9}⋅T_{n−1}. \nonumber
Therefore, T_n=\left(\frac{1}{9}\right)^n⋅\frac{\sqrt{3}}{4}. Since a new triangle is formed on each side of F_{n−1},
A_n=A_{n−1}+N_{n−1}⋅T_n=A_{n−1}+(3⋅4_{n−1})⋅\left(\frac{1}{9}\right)^n⋅\frac{\sqrt{3}}{4}=A_{n−1}+\frac{3}{4}⋅\left(\frac{4}{9}\right)^n⋅\frac{\sqrt{3}}{4}. \nonumber
Writing out the first few terms A_0,A_1,A_2, we see that
A_0=\frac{\sqrt{3}}{4}
A_1=A_0+\frac{3}{4}⋅\left(\frac{4}{9}\right)⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}+\frac{3}{4}⋅\left(\frac{4}{9}\right)⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}⋅\left(\frac{4}{9}\right)\right]
A_2=A_1+\frac{3}{4}⋅(\frac{4}{9})^2⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}⋅\left(\frac{4}{9}\right)\right]+\frac{3}{4}⋅\left(\frac{4}{9}\right)^2⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}[1+\frac{3}{4}⋅(\frac{4}{9})+\frac{3}{4}⋅\left(\frac{4}{9}\right)^2].
More generally,
A_n=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}\left(\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^n\right)\right].
Factoring 4/9 out of each term inside the inner parentheses, we rewrite our expression as
A_n=\frac{\sqrt{3}}{4}\left[1+\frac{1}{3}\left(1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}\right)\right].
The expression 1+\left(\frac{4}{9}\right)+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1} is a geometric sum. As shown earlier, this sum satisfies
1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}=\dfrac{1−(4/9)^n}{1−(4/9)}.
Substituting this expression into the expression above and simplifying, we conclude that
A_n=\frac{\sqrt{3}}{4}\left[1+\frac{1}{3}(\frac{1−(4/9)^n}{1−(4/9)})\right]=\frac{\sqrt{3}}{4}\left[\frac{8}{5}−\frac{3}{5}\left(\frac{4}{9}\right)^n\right]. \nonumber
Therefore, the area of Koch’s snowflake is
\displaystyle A=\lim_{n→∞}A_n=\frac{2\sqrt{3}}{5}.
Analysis
The Koch snowflake is interesting because it has finite area, yet infinite perimeter. Although at first this may seem impossible, recall that you have seen similar examples earlier in the text. For example, consider the region bounded by the curve y=1/x^2 and the x-axis on the interval [1,∞). Since the improper integral
∫^∞_1\frac{1}{x^2}\,dx \nonumber
converges, the area of this region is finite, even though the perimeter is infinite.
Telescoping Series
Consider the series \displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}. We discussed this series in Example \PageIndex{1c}, showing that the series converges by writing out the first several partial sums S_1, \, S_2, \, …, \, S_6 and noticing that they are all of the form S_k=\dfrac{k}{k+1}. Here we use a different technique to show that this series converges. By using partial fractions, we can write
\frac{1}{n(n+1)}=\frac{1}{n}−\frac{1}{n+1}. \nonumber
Therefore, the series can be written as
\displaystyle \sum_{n=1}^∞\left[\frac{1}{n}−\frac{1}{n+1}\right]=\left(1-\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)+⋯.
Writing out the first several terms in the sequence of partial sums {S_k}, we see that
S_1=1−\frac{1}{2}
S_2=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)=1−\frac{1}{3}
S_3=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)=1−\frac{1}{4}.
In general,
S_k=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)+⋯+\left(\frac{1}{k}−\frac{1}{k+1}\right)=1−\dfrac{1}{k+1}.
We notice that the middle terms cancel each other out, leaving only the first and last terms. In a sense, the series collapses like a spyglass with tubes that disappear into each other to shorten the telescope. For this reason, we call a series that has this property a telescoping series. For this series, since S_k=1−1/(k+1) and 1/(k+1)→0 as k→∞, the sequence of partial sums converges to 1, and therefore the series converges to 1.
Definition
A telescoping series is a series in which most of the terms cancel in each of the partial sums, leaving only some of the first terms and some of the last terms.
For example, any series of the form
\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=(b_1−b_2)+(b_2−b_3)+(b_3−b_4)+⋯
is a telescoping series. We can see this by writing out some of the partial sums. In particular, we see that
S_1=b_1−b_2
S_2=(b_1−b_2)+(b_2−b_3)=b_1−b_3
S_3=(b_1−b_2)+(b_2−b_3)+(b_3−b_4)=b_1−b_4.
In general, the k^{\text{th}} partial sum of this series is
S_k=b_1−b_{k+1}.
Since the k^{\text{th}} partial sum can be simplified to the difference of these two terms, the sequence of partial sums {S_k} will converge if and only if the sequence {b_{k+1}} converges. Moreover, if the sequence b_{k+1} converges to some finite number B, then the sequence of partial sums converges to b_1−B, and therefore
\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=b_1−B.
In the next example, we show how to use these ideas to analyze a telescoping series of this form.
Example \PageIndex{6}: Evaluating a Telescoping Series
Determine whether the telescoping series
\displaystyle \sum_{n=1}^∞\left[\cos\left(\frac{1}{n}\right)−\cos\left(\frac{1}{n+1}\right)\right]
converges or diverges. If it converges, find its sum.
Solution
By writing out terms in the sequence of partial sums, we can see that
S_1=\cos(1)−\cos(\frac{1}{2})
S_2=(\cos(1)−\cos(\frac{1}{2}))+(\cos(\frac{1}{2})−\cos(\frac{1}{3}))=\cos(1)−\cos(\frac{1}{3})
S_3=(\cos(1)−\cos(\frac{1}{2}))+(\cos(\frac{1}{2})−\cos(\frac{1}{3}))+(\cos(\frac{1}{3})−\cos(\frac{1}{4}))
=\cos(1)−\cos(\frac{1}{4}).
In general,
S_k=\cos(1)−\cos\left(\frac{1}{k+1}\right).
Since 1/(k+1)→0 as k→∞ and \cos x is a continuous function, \cos(1/(k+1))→\cos(0)=1. Therefore, we conclude that S_k→\cos(1)−1. The telescoping series converges and the sum is given by
\displaystyle \sum_{n=1}^∞\left[\cos\left(\frac{1}{n}\right)−\cos\left(\frac{1}{n+1}\right)\right]=\cos(1)−1.
Exercise \PageIndex{5}
Determine whether \displaystyle \sum^∞_{n=1}[e^{1/n}−e^{1/(n+1)}] converges or diverges. If it converges, find its sum.
- Hint
-
Write out the sequence of partial sums to see which terms cancel.
- Answer
-
e−1
Euler’s Constant
We have shown that the harmonic series \displaystyle \sum^∞_{n=1}\frac{1}{n} diverges. Here we investigate the behavior of the partial sums S_k as k→∞. In particular, we show that they behave like the natural logarithm function by showing that there exists a constant γ such that
\displaystyle \sum_{n=1}^k\left(\frac{1}{n}−\ln k\right)→γ as k→∞.
This constant γ is known as Euler’s constant.
1. Let \displaystyle T_k=\sum_{n=1}^k\left(\frac{1}{n}−\ln k\right). Evaluate T_k for various values of k.
2. For T_k as defined in part 1. show that the sequence {T_k} converges by using the following steps.
a. Show that the sequence {T_k} is monotone decreasing. (Hint: Show that \ln(1+1/k>1/(k+1))
b. Show that the sequence {T_k} is bounded below by zero. (Hint: Express \ln k as a definite integral.)
c. Use the Monotone Convergence Theorem to conclude that the sequence {T_k} converges. The limit γ is Euler’s constant.
3. Now estimate how far T_k is from γ for a given integer k. Prove that for k≥1, 0<T_k−γ≤1/k by using the following steps.
a. Show that \ln(k+1)−\ln k<1/k.
b. Use the result from part a. to show that for any integer k,
T_k−T_{k+1}<\frac{1}{k}−\frac{1}{k+1}. \nonumber
c. For any integers k and j such that j>k, express T_k−T_j as a telescoping sum by writing
T_k−T_j=(T_k−T_{k+1})+(T_{k+1}−T_{k+2})+(T_{k+2}−T_{k+3})+⋯+(T_{j−1}−T_j). \nonumber
Use the result from part b. combined with this telescoping sum to conclude that
T_k−T_j<\frac{1}{k}−\frac{1}{j}. \nonumber
a. Apply the limit to both sides of the inequality in part c. to conclude that
T_k−γ≤\frac{1}{k}. \nonumber
e. Estimate γ to an accuracy of within 0.001.
Key Concepts
- Given the infinite series
\displaystyle \sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯
and the corresponding sequence of partial sums {S_k} where
\displaystyle S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k,
the series converges if and only if the sequence {S_k} converges.
- The geometric series \displaystyle \sum^∞_{n=1}ar^{n−1} converges if |r|<1 and diverges if |r|≥1. For |r|<1,
\displaystyle \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}.
- The harmonic series
\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+⋯
diverges.
- A series of the form \displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=[b_1−b_2]+[b_2−b_3]+[b_3−b_4]+⋯+[b_n−b_{n+1}]+⋯ is a telescoping series. The k^{\text{th}} partial sum of this series is given by S_k=b_1−b_{k+1}. The series will converge if and only if \displaystyle \lim_{k→∞} b_{k+1} exists. In that case,
\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=b_1−\lim_{k→∞}(b_{k+1}).
Key Equations
- Harmonic series
\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯
- Sum of a geometric series
\displaystyle \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r} for |r|<1
Glossary
- convergence of a series
- a series converges if the sequence of partial sums for that series converges
- divergence of a series
- a series diverges if the sequence of partial sums for that series diverges
- geometric series
- a geometric series is a series that can be written in the form
\displaystyle \sum_{n=1}^∞ar^{n−1}=a+ar+ar^2+ar^3+⋯
- harmonic series
- the harmonic series takes the form
\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+⋯
- infinite series
- an infinite series is an expression of the form
\displaystyle a_1+a_2+a_3+⋯=\sum_{n=1}^∞a_n
- partial sum
-
the k^{\text{th}} partial sum of the infinite series \displaystyle \sum^∞_{n=1}a_n is the finite sum
\displaystyle S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k
- telescoping series
- a telescoping series is one in which most of the terms cancel in each of the partial sums


