9.2E: Exercises for Infinite Series

In exercises 1 - 4, use sigma notation to write each expressions as an infinite series.

1)

Answer

2)

3)

Answer

4)

In exercises 5 - 8, compute the first four partial sums for the series having term starting with as follows.

5)

Answer

6)

7)

Answer

8)

In exercises 9 - 12, compute the general term of the series with the given partial sum . If the sequence of partial sums converges, find its limit .

9)

Answer

Since the series converges to

10)

11)

Answer

The series diverges because the partial sums are unbounded.
That is,

12)

For each series in exercises 13 - 16, use the sequence of partial sums to determine whether the series converges or diverges.

13)

Answer

In general so the series diverges.
Note that the Term Test for Divergence could also be used to prove that this series diverges.

14)

15) Hint: Use a partial fraction decomposition like that for

Answer

The pattern is
Then so the series converges to

16) Hint: Follow the reasoning for

Suppose that , that , that , and . Use this information to find the sum of the indicated series in exercises 17 - 20.

17)

Answer

18)

19)

Answer

20)

In exercises 21 - 26, state whether the given series converges or diverges and explain why.

21) (Hint: Rewrite using a change of index.)

Answer

The series diverges,

22) (Hint: Rewrite using a change of index.)

23)

Answer

This is a convergent geometric series, since

24)

25)

Answer

This is a convergent geometric series, since

26)

For each in exercises 27 - 30, write its sum as a geometric series of the form . State whether the series converges and if it does, find the exact value of its sum.

27) and for

Answer

, converges to

28) and for

29) and for .

Answer

converges to

30) and for .

In exercises 31 - 34, use the identity (which is true for ) to express each function as a geometric series in the indicated term.

31) in

Answer

32) in

33) in

Answer

34) in

In exercises 35 - 38, evaluate the telescoping series or state whether the series diverges.

35)

Answer

as

36)

37)

Answer

diverges

38)

Express each series in exercises 39 - 42 as a telescoping sum and evaluate its partial sum.

39)

Answer

40) (Hint: Factor denominator and use partial fractions.)

41)

Answer

and

42) (Hint: Look at .

A general telescoping series is one in which all but the first few terms cancel out after summing a given number of successive terms.

43) Let in which as Find .

Answer

44) in which as . Find .

45) Suppose that where as . Find a condition on the coefficients that make this a general telescoping series.

Answer

46) Evaluate (Hint: )

47) Evaluate

Answer

48) Find a formula for where is a positive integer.

49) [T] Define a sequence . Use the graph of to verify that is increasing. Plot for and state whether it appears that the sequence converges.

Answer

converges to is a sum of rectangles of height over the interval 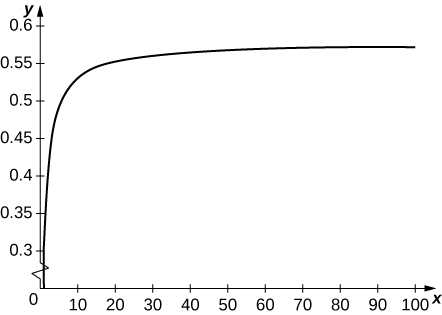which lie above the graph of .

50) [T] Suppose that equal uniform rectangular blocks are stacked one on top of the other, allowing for some overhang. Archimedes’ law of the lever implies that the stack of blocks is stable as long as the center of mass of the top blocks lies at the edge of the bottom block. Let denote the position of the edge of the bottom block, and think of its position as relative to the center of the next-to-bottom block. This implies that or . Use this expression to compute the maximum overhang (the position of the edge of the top block over the edge of the bottom block.) See the following figure.

Each of the following infinite series converges to the given multiple of or .

In each case, find the minimum value of such that the partial sum of the series accurately approximates the left-hand side to the given number of decimal places, and give the desired approximate value. Up to 15 decimals place,

51) [T] error

Answer

52) [T] error

53) [T] error

Answer

54) [T] , error

55) [T] A fair coin is one that has probability of coming up heads when flipped.

a. What is the probability that a fair coin will come up tails times in a row?

b. Find the probability that a coin comes up heads for the first time after an even number of coin flips.

Answer

a. The probability of any given ordered sequence of outcomes for coin flips is .
b. The probability of coming up heads for the first time on the th flip is the probability of the sequence which is . The probability of coming up heads for the first time on an even flip is or .

56) [T] Find the probability that a fair coin is flipped a multiple of three times before coming up heads.

57) [T] Find the probability that a fair coin will come up heads for the second time after an even number of flips.

Answer

58) [T] Find a series that expresses the probability that a fair coin will come up heads for the second time on a multiple of three flips.

59) [T] The expected number of times that a fair coin will come up heads is defined as the sum over of times the probability that the coin will come up heads exactly times in a row, or . Compute the expected number of consecutive times that a fair coin will come up heads.

Answer

as can be shown using summation by parts

60) [T] A person deposits at the beginning of each quarter into a bank account that earns annual interest compounded quarterly (four times a year).

a. Show that the interest accumulated after quarters is

b. Find the first eight terms of the sequence.

c. How much interest has accumulated after years?

61) [T] Suppose that the amount of a drug in a patient’s system diminishes by a multiplicative factor each hour. Suppose that a new dose is administered every hours. Find an expression that gives the amount in the patient’s system after hours for each in terms of the dosage and the ratio . (Hint: Write , where , and sum over values from the different doses administered.)

Answer

The part of the first dose after hours is , the part of the second dose is , and, in general, the part remaining of the dose is , so

62) [T] A certain drug is effective for an average patient only if there is at least mg per kg in the patient’s system, while it is safe only if there is at most mg per kg in an average patient’s system. Suppose that the amount in a patient’s system diminishes by a multiplicative factor of each hour after a dose is administered. Find the maximum interval of hours between doses, and corresponding dose range (in mg/kg) for this that will enable use of the drug to be both safe and effective in the long term.

63) Suppose that is a sequence of numbers. Explain why the sequence of partial sums of is increasing.

Answer

64) [T] Suppose that is a sequence of positive numbers and the sequence of partial sums of is bounded above. Explain why converges. Does the conclusion remain true if we remove the hypothesis ?

65) [T] Suppose that and that, for given numbers and , one defines and . Does converge? If so, to what? (Hint: First argue that for all and is increasing.)

Answer

Since and since . If for some , then there is a smallest . For this , so , a contradiction. Thus and for all , so is increasing and bounded by . Let . If , then , but we can find n such that , which implies that , contradicting that Sn is increasing to . Thus

66) [T] A version of von Bertalanffy growth can be used to estimate the age of an individual in a homogeneous species from its length if the annual increase in year satisfies , with as the length at year as a limiting length, and as a relative growth constant. If and numerically estimate the smallest value of n such that . Note that Find the corresponding when

67) [T] Suppose that is a convergent series of positive terms. Explain why

Answer

Let and . Then eventually becomes arbitrarily close to , which means that becomes arbitrarily small as

68) [T] Find the length of the dashed zig-zag path in the following figure.

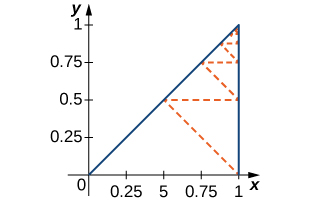
69) [T] Find the total length of the dashed path in the following figure.

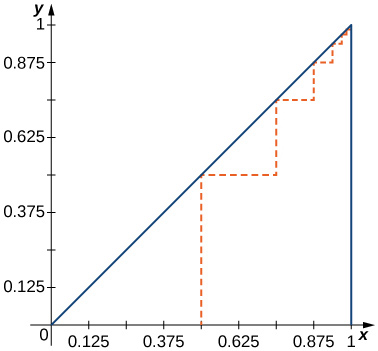
Answer

.

70) [T] The Sierpinski triangle is obtained from a triangle by deleting the middle fourth as indicated in the first step, by deleting the middle fourths of the remaining three congruent triangles in the second step, and in general deleting the middle fourths of the remaining triangles in each successive step. Assuming that the original triangle is shown in the figure, find the areas of the remaining parts of the original triangle after steps and find the total length of all of the boundary triangles after steps.

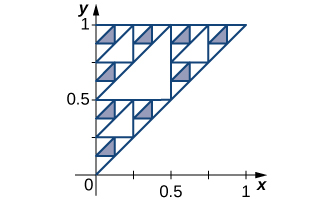
71) [T] The Sierpinski gasket is obtained by dividing the unit square into nine equal sub-squares, removing the middle square, then doing the same at each stage to the remaining sub-squares. The figure shows the remaining set after four iterations. Compute the total area removed after stages, and compute the length the total perimeter of the remaining set after stages.

Answer

At stage one a square of area is removed, at stage one removes squares of area , at stage three one removes squares of area , and so on. The total removed area after stages is as The total perimeter is