14.6E: Exercises for Section 14.6

Last updated

Jun 1, 2021
Save as PDF

Page ID: 66954

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

In exercises 1 - 12, the region $R$ occupied by a lamina is shown in a graph. Find the mass of $R$ with the density function $\rho$ .

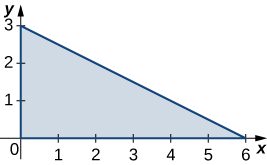
1. $R$ is the triangular region with vertices $(0,0), \space (0,3)$ , and $(6,0); \space \rho (x,y) = xy$ .

$A right triangle bounded by the x and y axes and the line y = negative x/2 + 3.$

Answer: $\frac{27}{2}$

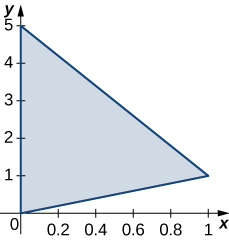
2. $R$ is the triangular region with vertices $(0,0), \space (1,1)$ , and $(0,5); \space \rho (x,y) = x + y$ .

$A triangle bounded by the y axis, the line x = y, and the line y = negative 4x + 5.$

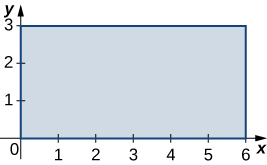
3. $R$ is the rectangular region with vertices $(0,0), \space (0,3), \space (6,3)$ and $(6,0); \space \rho (x,y) = \sqrt{xy}$ .

$A rectangle bounded by the x and y axes and the lines x = 6 and y = 3.$

Answer: $24\sqrt{2}$

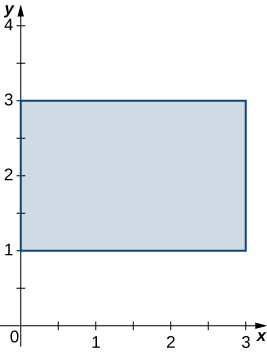
4. $R$ is the rectangular region with vertices $(0,1), \space (0,3), \space (3,3)$ and $(3,1); \space \rho (x,y) = x^2y$ .

$A rectangle bounded by the y axis, the lines y = 1 and 3, and the line x = 3.$

5. $R$ is the trapezoidal region determined by the lines $y = - \frac{1}{4}x + \frac{5}{2}, \space y = 0, \space y = 2$ , and $x = 0; \space \rho (x,y) = 3xy$ .

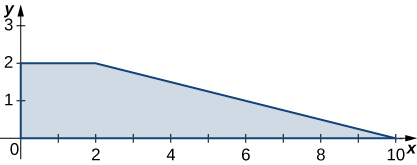
$A trapezoid bounded by the x and y axes, the line y = 2, and the line y = negative x/4 + 2.5.$

Answer: $76$

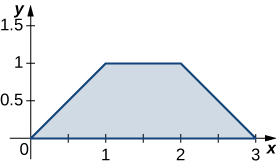
is the trapezoidal region determined by the lines $y = 0, \space y = 1, \space y = x$ and $y = -x + 3; \space \rho (x,y) = 2x + y$ .

$A trapezoid bounded by the x axis, the line y = 1, the line y = x, and the line y = negative x + 3.$

is the disk of radius $2$ centered at $(1,2); \space \rho(x,y) = x^2 + y^2 - 2x - 4y + 5$ .

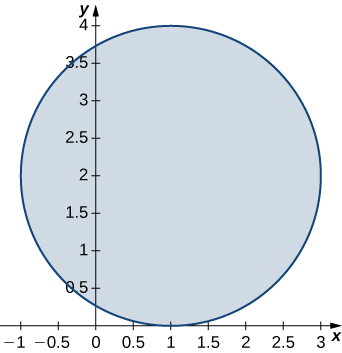
Answer: $8\pi$

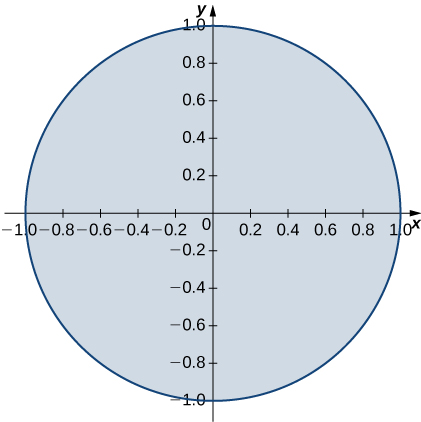
is the unit disk; $\rho (x,y) = 3x^4 + 6x^2y^2 + 3y^4$ .

$A circle with radius 1 and center the origin.$

is the region enclosed by the ellipse $x^2 + 4y^2 = 1; \space \rho(x,y) = 1$ .

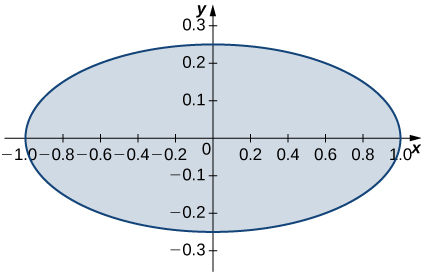
$An ellipse with center the origin, major axis 2, and minor axis 0.5.$

Answer: $\frac{\pi}{2}$

10. $R = \big\{(x,y) \,|\, 9x^2 + y^2 \leq 1, \space x \geq 0, \space y \geq 0\big\} ; \space \rho (x,y) = \sqrt{9x^2 + y^2}$ .

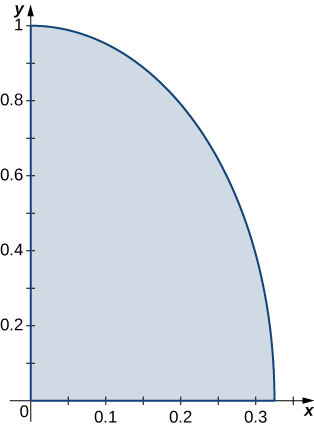
$The quarter section of an ellipse in the first quadrant with center the origin, major axis 2, and minor axis roughly 0.64.$

is the region bounded by $y = x, \space y = -x, \space y = x + 2, \space y = -x + 2; \space \rho(x,y) = 1$ .

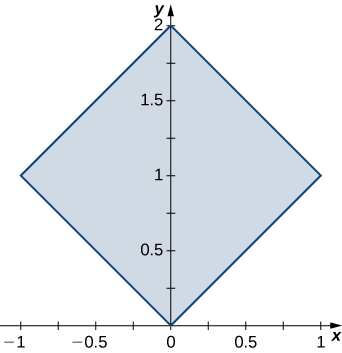
$A square with side length square root of 2 rotated 45 degrees, with corners at the origin, (2, 0), (1, 1), and (negative 1, 1).$

Answer: $2$

is the region bounded by $y = \frac{1}{x}, \space y = \frac{2}{x}, \space y = 1$ , and $y = 2; \space \rho (x,y) = 4(x + y)$ .

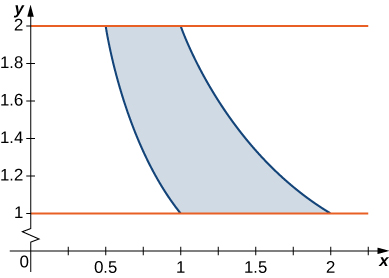
$A complex region between 2 and 1 that sweeps down and to the right with boundaries y = 1/x and y = 2/x.$

In exercises 13 - 24, consider a lamina occupying the region $R$ and having the density function $\rho$ given in the preceding group of exercises. Use a computer algebra system (CAS) to answer the following questions.

a. Find the moments $M_x$ and $M_y$ about the $x$ -axis and $y$ -axis, respectively.

b. Calculate and plot the center of mass of the lamina.

c. [T] Use a CAS to locate the center of mass on the graph of $R$ .

13. [T] $R$ is the triangular region with vertices $(0,0), \space (0,3)$ , and $(6,0); \space \rho (x,y) = xy$ .

Answer

a. $M_x = \frac{81}{5}, \space M_y = \frac{162}{5}$ ;
b. $\bar{x} = \frac{12}{5}, \space \bar{y} = \frac{6}{5}$ ;
c.

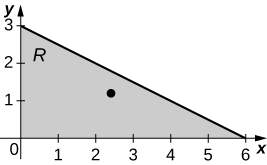
$A triangular region R bounded by the x and y axes and the line y = negative x/2 + 3, with a point marked at (12/5, 6/5).$

is the triangular region with vertices $(0,0), \space (1,1)$ , and $(0,5); \space \rho (x,y) = x + y$ .

is the rectangular region with vertices $(0,0), \space (0,3), \space (6,3)$ , and $(6,0); \space \rho (x,y) = \sqrt{xy}$ .

Answer

a. $M_x = \frac{216\sqrt{2}}{5}, \space M_y = \frac{432\sqrt{2}}{5}$ ;
b. $\bar{x} = \frac{18}{5}, \space \bar{y} = \frac{9}{5}$ ;
c.

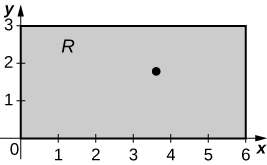
$A rectangle R bounded by the x and y axes and the lines x = 6 and y = 3 with point marked (18/5, 9/5).$

is the rectangular region with vertices $(0,1), \space (0,3), \space (3,3)$ , and $(3,1); \space \rho (x,y) = x^2y$ .

17. [T] $R$ is the trapezoidal region determined by the lines $y = - \frac{1}{4}x + \frac{5}{2}, \space y = 0, \space y = 2$ , and $x = 0; \space \rho (x,y) = 3xy$ .

Answer

a. $M_x = \frac{368}{5}, \space M_y = \frac{1552}{5}$ ;
b. $\bar{x} = \frac{92}{95}, \space \bar{y} = \frac{388}{95}$ ;
c.

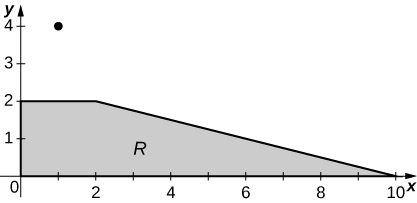
$A trapezoid R bounded by the x and y axes, the line y = 2, and the line y = negative x/4 + 2.5 with the point marked (92/95, 388/95).$

18. [T] $R$ is the trapezoidal region determined by the lines $y = 0, \space y = 1, \space y = x,$ and $y = -x + 3; \space \rho (x,y) = 2x + y$ .

19. [T] is the disk of radius $2$ centered at $(1,2); \space \rho(x,y) = x^2 + y^2 - 2x - 4y + 5$ .

Answer

a. $M_x = 16\pi, \space M_y = 8\pi$ ;
b. $\bar{x} = 1, \space \bar{y} = 2$ ;
c.

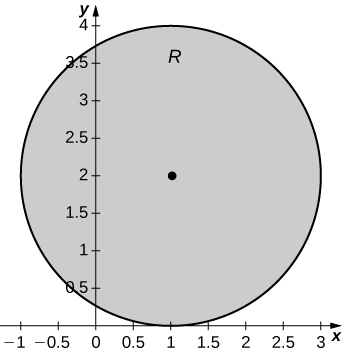
$A circle with radius 2 centered at (1, 2), which is tangent to the x axis at (1, 0) and has pointed marked at the center (1, 2).$

is the unit disk; $\rho (x,y) = 3x^4 + 6x^2y^2 + 3y^4$ .

21. [T] is the region enclosed by the ellipse $x^2 + 4y^2 = 1; \space \rho(x,y) = 1$ .

Answer

a. $M_x = 0, \space M_y = 0)$ ;
b. $\bar{x} = 0, \space \bar{y} = 0$ ;
c.

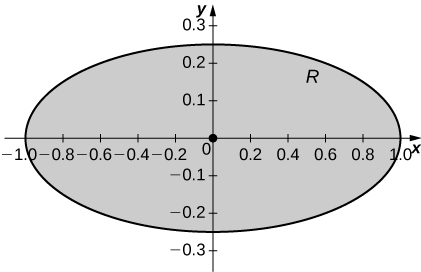
$An ellipse R with center the origin, major axis 2, and minor axis 0.5, with point marked at the origin.$

22. [T] $R = \big\{(x,y) \,|\, 9x^2 + y^2 \leq 1, \space x \geq 0, \space y \geq 0\big\} ; \space \rho (x,y) = \sqrt{9x^2 + y^2}$ .

23. [T] $R$ is the region bounded by $y = x, \space y = -x, \space y = x + 2$ , and $y = -x + 2; \space \rho (x,y) = 1$ .

Answer

a. $M_x = 2, \space M_y = 0)$ ;
b. $\bar{x} = 0, \space \bar{y} = 1$ ;
c.

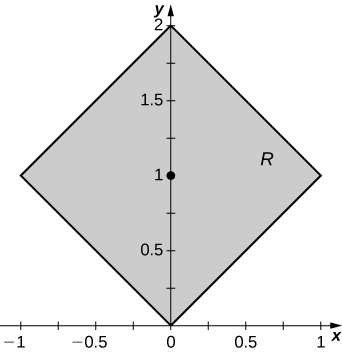
$A square R with side length square root of 2 rotated 45 degrees, with corners at the origin, (2, 0), (1, 1), and (negative 1, 1). A point is marked at (0, 1).$

is the region bounded by $y = \frac{1}{x}, \space y = \frac{2}{x}, \space y = 1$ , and $y = 2; \space \rho (x,y) = 4(x + y)$ .

In exercises 25 - 36, consider a lamina occupying the region $R$ and having the density function $\rho$ given in the first two groups of Exercises.

a. Find the moments of inertia $I_x$ , $I_y$ and $I_0$ about the $x$ -axis, $y$ -axis, and origin, respectively.

b. Find the radii of gyration with respect to the $x$ -axis, $y$ -axis, and origin, respectively.

25. $R$ is the triangular region with vertices $(0,0), \space (0,3)$ , and $(6,0); \space \rho (x,y) = xy$ .

Answer: a. $I_x = \frac{243}{10}, \space I_y = \frac{486}{5}$ , and $I_0 = \frac{243}{2}$ ;
b. $R_x = \frac{3\sqrt{5}}{5}, \space R_y = \frac{6\sqrt{5}}{5}$ , and $R_0 = 3$

is the triangular region with vertices $(0,0), \space (1,1)$ , and $(0,5); \space \rho (x,y) = x + y$ .

is the rectangular region with vertices $(0,0), \space (0,3), \space (6,3)$ , and $(6,0); \space \rho (x,y) = \sqrt{xy}$ .

Answer: a. $I_x = \frac{2592\sqrt{2}}{7}, \space I_y = \frac{648\sqrt{2}}{7}$ , and $I_0 = \frac{3240\sqrt{2}}{7}$ ;
b. $R_x = \frac{6\sqrt{21}}{7}, \space R_y = \frac{3\sqrt{21}}{7}$ , and $R_0 = \frac{3\sqrt{106}}{7}$

is the rectangular region with vertices $(0,1), \space (0,3), \space (3,3)$ , and $(3,1); \space \rho (x,y) = x^2y$ .

29. $R$ is the trapezoidal region determined by the lines $y = - \frac{1}{4}x + \frac{5}{2}, \space y = 0, \space y = 2$ , and x = 0; \space \rho (x,y) = 3xy\).

Answer: a. $I_x = 88, \space I_y = 1560$ , and $I_0 = 1648$ ;
b. $R_x = \frac{\sqrt{418}}{19}, \space R_y = \frac{\sqrt{7410}}{10}$ , and $R_0 = \frac{2\sqrt{1957}}{19}$

30. $R$ is the trapezoidal region determined by the lines $y = 0, \space y = 1, \space y = x$ , and y = -x + 3; \space \rho (x,y) = 2x + y\).

is the disk of radius $2$ centered at $(1,2); \space \rho(x,y) = x^2 + y^2 - 2x - 4y + 5$ .

Answer: a. $I_x = \frac{128\pi}{3}, \space I_y = \frac{56\pi}{3}$ , and $I_0 = \frac{184\pi}{3}$ ;
b. $R_x = \frac{4\sqrt{3}}{3}, \space R_y = \frac{\sqrt{21}}{2}$ , and $R_0 = \frac{\sqrt{69}}{3}$

is the unit disk; $\rho (x,y) = 3x^4 + 6x^2y^2 + 3y^4$ .

is the region enclosed by the ellipse $x^2 + 4y^2 = 1; \space \rho(x,y) = 1$ .

Answer: a. $I_x = \frac{\pi}{32}, \space I_y = \frac{\pi}{8}$ , and $I_0 = \frac{5\pi}{32}$ ;
b. $R_x = \frac{1}{4}, \space R_y = \frac{1}{2}$ , and $R_0 = \frac{\sqrt{5}}{4}$

34. $R = \big\{(x,y) \,|\, 9x^2 + y^2 \leq 1, \space x \geq 0, \space y \geq 0\big\} ; \space \rho (x,y) = \sqrt{9x^2 + y^2}$ .

35. $R$ is the region bounded by $y = x, \space y = -x, \space y = x + 2$ , and $y = -x + 2; \space \rho (x,y) = 1$ .

Answer: a. $I_x = \frac{7}{3}, \space I_y = \frac{1}{3}$ , and $I_0 = \frac{8}{3}$ ;
b. $R_x = \frac{\sqrt{42}}{6}, \space R_y = \frac{\sqrt{6}}{6}$ , and $R_0 = \frac{2\sqrt{3}}{3}$

is the region bounded by $y = \frac{1}{x}, \space y = \frac{2}{x}, \space y = 1$ , and $y = 2; \space \rho (x,y) = 4(x + y)$ .

37. Let $Q$ be the solid unit cube. Find the mass of the solid if its density $\rho$ is equal to the square of the distance of an arbitrary point of $Q$ to the $xy$ -plane.

Answer: $m = \frac{1}{3}$

38. Let $Q$ be the solid unit hemisphere. Find the mass of the solid if its density $\rho$ is proportional to the distance of an arbitrary point of $Q$ to the origin.

39. The solid $Q$ of constant density $1$ is situated inside the sphere $x^2 + y^2 + z^2 = 16$ and outside the sphere $x^2 + y^2 + z^2 = 1$ . Show that the center of mass of the solid is not located within the solid.

40. Find the mass of the solid $Q = \big\{ (x,y,z) \,|\, 1 \leq x^2 + z^2 \leq 25, \space y \leq 1 - x^2 - z^2 \big\}$ whose density is $\rho (x,y,z) = k$ , where $k > 0$ .

41. [T] The solid $Q = \big\{ (x,y,z) \,|\, x^2 + y^2 \leq 9, \space 0 \leq z \leq 1, \space x \geq 0, \space y \geq 0\big\}$ has density equal to the distance to the $xy$ -plane. Use a CAS to answer the following questions.

a. Find the mass of $Q$ .

b. Find the moments $M_{xy}, \space M_{xz}$ and $M_{yz}$ about the $xy$ -plane, $xz$ -plane, and $yz$ -plane, respectively.

c. Find the center of mass of $Q$ .

d. Graph $Q$ and locate its center of mass.

Answer

a. $m = \frac{9\pi}{4}$ ;
b. $M_{xy} = \frac{3\pi}{2}, \space M_{xz} = \frac{81}{8}, \space M_{yz} = \frac{81}{8}$ ;
c. $\bar{x} = \frac{9}{2\pi}, \space \bar{y} = \frac{9}{2\pi}, \space \bar{z} = \frac{2}{3}$ ;
d.

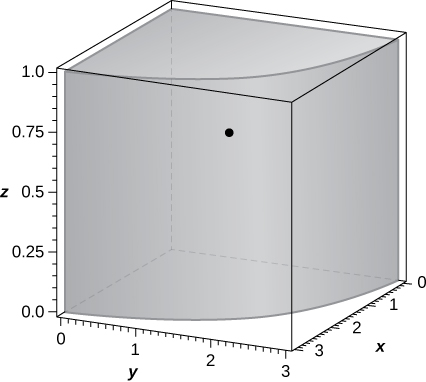
$A quarter cylinder in the first quadrant with height 1 and radius 3. A point is marked at (9/(2 pi), 9/(2 pi), 2/3).$

$Q = \big\{ (x,y,z) \,|\, 0 \leq x \leq 1, \space 0 \leq y \leq 2, \space 0 \leq z \leq 3\big\}$ with the density function $\rho(x,y,z) = x + y + 1$ .

a. Find the mass of $Q$ .

b. Find the moments $M_{xy}, \space M_{xz}$ and $M_{yz}$ about the $xy$ -plane, $xz$ -plane, and $yz$ -plane, respectively.

c. Find the center of mass of $Q$ .

43. [T] The solid $Q$ has the mass given by the triple integral $\displaystyle \int_{-1}^1 \int_0^{\pi/4} \int_0^1 r^2 \, dr \space d\theta \space dz.$

Use a CAS to answer the following questions.

Show that the center of mass of $Q$ is located in the $xy$ -plane.
Graph $Q$ and locate its center of mass.

Answer

$\bar{x} = \frac{3\sqrt{2}}{2\pi}$ , $\bar{y} = \frac{3(2-\sqrt{2})}{2\pi}, \space \bar{z} = 0$ ; 2. the solid $Q$ and its center of mass are shown in the following figure.

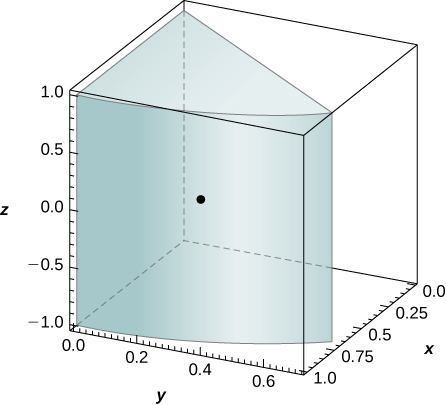
$A wedge from a cylinder in the first quadrant with height 2, radius 1, and angle roughly 45 degrees. A point is marked at (3 times the square root of 2/(2 pi), 3 times (2 minus the square root of 2)/(2 pi), 0).$

44. The solid $Q$ is bounded by the planes $x + 4y + z = 8, \space x = 0, \space y = 0$ , and $z = 0$ . Its density at any point is equal to the distance to the $xz$ -plane. Find the moments of inertia of the solid about the $xz$ -plane.

45. The solid $Q$ is bounded by the planes $x + y + z = 3, \space x = 0, \space y = 0$ , and $z = 0$ . Its density is $\rho(x,y,z) = x + ay$ , where $a > 0$ . Show that the center of mass of the solid is located in the plane $z = \frac{3}{5}$ for any value of $a$ .

46. Let $Q$ be the solid situated outside the sphere $x^2 + y^2 + z^2 = z$ and inside the upper hemisphere $x^2 + y^2 + z^2 = R^2$ , where $R > 1$ . If the density of the solid is $\rho (x,y,z) = \frac{1}{\sqrt{x^2+y^2+z^2}}$ , find $R$ such that the mass of the solid is $\frac{7\pi}{2}.$

47. The mass of a solid $Q$ is given by $\displaystyle \int_0^2 \int_0^{\sqrt{4-x^2}} \int_{\sqrt{x^2+y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2)^n \, dz \space dy \space dx,$ where $n$ is an integer. Determine $n$ such the mass of the solid is $(2 - \sqrt{2}) \pi$ .

Answer: $n = -2$

48. Let $Q$ be the solid bounded above the cone $x^2 + y^2 = z^2$ and below the sphere $x^2 + y^2 + z^2 - 4z = 0$ . Its density is a constant $k > 0$ . Find $k$ such that the center of mass of the solid is situated $7$ units from the origin.

49. The solid $Q = \big\{(x,y,z) \,|\, 0 \leq x^2 + y^2 \leq 16, \space x \geq 0, \space y \geq 0, \space 0 \leq z \leq x\big\}$ has the density $\rho (x,y,z) = k$ . Show that the moment $M_{xy}$ about the $xy$ -plane is half of the moment $M_{yz}$ about the $yz$ -plane.

50. The solid $Q$ is bounded by the cylinder $x^2 + y^2 = a^2$ , the paraboloid $b^2 - z = x^2 + y^2$ , and the $xy$ -plane, where $0 < a < b$ . Find the mass of the solid if its density is given by $\rho(x,y,z) = \sqrt{x^2 + y^2}$ .

51. Let $Q$ be a solid of constant density $k$ , where $k > 0$ , that is located in the first octant, inside the circular cone $x^2 + y^2 = 9(z - 1)^2$ , and above the plane $z = 0$ . Show that the moment $M_{xy}$ about the $xy$ -plane is the same as the moment $M_{yz}$ about the $xz$ -plane.

52. The solid $Q$ has the mass given by the triple integral $\displaystyle \int_0^1 \int_0^{\pi/2} \int_0^{r^3} (r^4 + r) \space dz \space d\theta \space dr.$

a. Find the density of the solid in rectangular coordinates.

b. Find the moment $M_{xy}$ about the $xy$ -plane.

53. The solid $Q$ has the moment of inertia $I_x$ about the $yz$ -plane given by the triple integral $\displaystyle \int_0^2 \int_{-\sqrt{4-y^2}}^{\sqrt{4-y^2}} \int_{\frac{1}{2}(x^2+y^2)}^{\sqrt{x^2+y^2}} (y^2 + z^2)(x^2 + y^2) \, dz \space dx \space dy.$

a. Find the density of $Q$ .

b. Find the moment of inertia $I_z$ about the $xy$ -plane.

Answer: a. $\rho (x,y,z) = x^2 + y^2$ ;
b. $\frac{16\pi}{7}$

54. The solid $Q$ has the mass given by the triple integral $\displaystyle \int_0^{\pi/4} \int_0^{2 \space sec \space \theta} \int_0^1 (r^3 \cos \theta \sin \theta + 2r) \, dz \space dr \space d\theta.$

a. Find the density of the solid in rectangular coordinates.

b. Find the moment $M_{xz}$ about the $xz$ -plane.

55. Let $Q$ be the solid bounded by the $xy$ -plane, the cylinder $x^2 + y^2 = a^2$ , and the plane $z = 1$ , where $a > 1$ is a real number. Find the moment $M_{xy}$ of the solid about the $xy$ -plane if its density given in cylindrical coordinates is $\rho(x,y,z) = \frac{d^2f}{dr^2} (r)$ , where $f$ is a differentiable function with the first and second derivatives continuous and differentiable on $(0,a)$ .

Answer: $M_{xy} = \pi (f(0) - f(a) + af'(a))$

56. A solid $Q$ has a volume given by $\displaystyle \iint_D \int_a^b \, dA \space dz$ , where $D$ is the projection of the solid onto the $xy$ -plane and $a < b$ are real numbers, and its density does not depend on the variable $z$ . Show that its center of mass lies in the plane $z = \frac{a+b}{2}$ .

57. Consider the solid enclosed by the cylinder $x^2 + z^2 = a^2$ and the planes $y = b$ and $y = c$ , where $a > 0$ and $b < c$ are real numbers. The density of $Q$ is given by $\rho(x,y,z) = f'(y)$ , where $f$ is a differential function whose derivative is continuous on $(b,c)$ . Show that if $f(b) = f(c)$ , then the moment of inertia about the $xz$ -plane of $Q$ is null.

58. [T] The average density of a solid $Q$ is defined as $\displaystyle \rho_{ave} = \frac{1}{V(Q)} \iiint_Q \rho(x,y,z) \, dV = \frac{m}{V(Q)},$ where $V(Q)$ and $m$ are the volume and the mass of $Q$ , respectively. If the density of the unit ball centered at the origin is $\rho (x,y,z) = e^{-x^2-y^2-z^2}$ , use a CAS to find its average density. Round your answer to three decimal places.

59. Show that the moments of inertia $I_x, \space I_y$ , and $I_z$ about the $yz$ -plane, $xz$ -plane, and $xy$ -plane, respectively, of the unit ball centered at the origin whose density is $\rho (x,y,z) = e^{-x^2-y^2-z^2}$ are the same. Round your answer to two decimal places.

Answer: $I_x = I_y = I_z \approx 0.84$

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

Search

Text Color

Text Size

Margin Size

Font Type

Contributors