In exercises 1 - 12, the region \(R\) occupied by a lamina is shown in a graph. Find the mass of \(R\) with the density function \(\rho\).
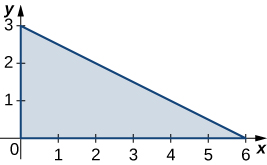
1. \(R\) is the triangular region with vertices \((0,0), \space (0,3)\), and \((6,0); \space \rho (x,y) = xy\).
- Answer
- \(\frac{27}{2}\)
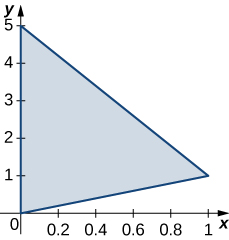
2. \(R\) is the triangular region with vertices \((0,0), \space (1,1)\), and \((0,5); \space \rho (x,y) = x + y\).
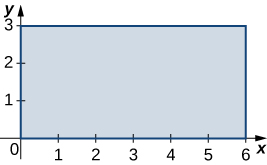
3. \(R\) is the rectangular region with vertices \((0,0), \space (0,3), \space (6,3) \) and \((6,0); \space \rho (x,y) = \sqrt{xy}\).
- Answer
- \(24\sqrt{2}\)
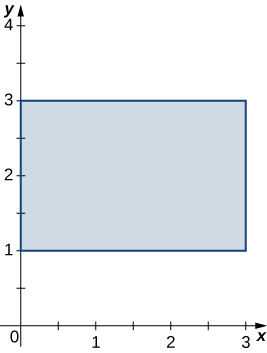
4. \(R\) is the rectangular region with vertices \((0,1), \space (0,3), \space (3,3)\) and \( (3,1); \space \rho (x,y) = x^2y\).
5. \(R\) is the trapezoidal region determined by the lines \(y = - \frac{1}{4}x + \frac{5}{2}, \space y = 0, \space y = 2\), and \(x = 0; \space \rho (x,y) = 3xy\).
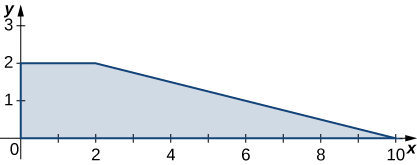
- Answer
- \(76\)
6. \(R\) is the trapezoidal region determined by the lines \(y = 0, \space y = 1, \space y = x\) and \(y = -x + 3; \space \rho (x,y) = 2x + y\).
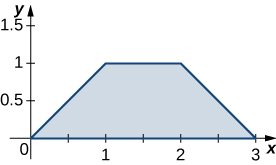
7. \(R\) is the disk of radius \(2\) centered at \((1,2); \space \rho(x,y) = x^2 + y^2 - 2x - 4y + 5\).
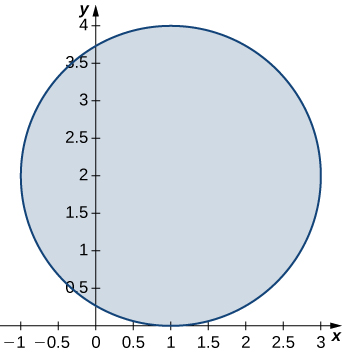
- Answer
- \(8\pi\)
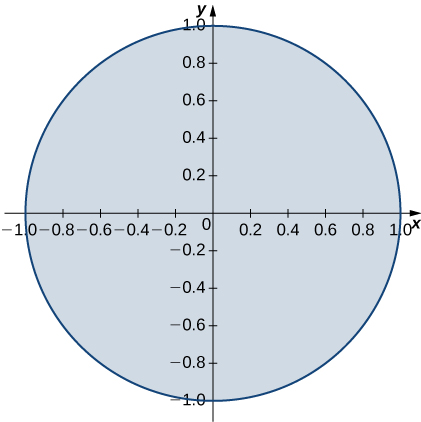
8. \(R\) is the unit disk; \(\rho (x,y) = 3x^4 + 6x^2y^2 + 3y^4\).
9. \(R\) is the region enclosed by the ellipse \(x^2 + 4y^2 = 1; \space \rho(x,y) = 1\).
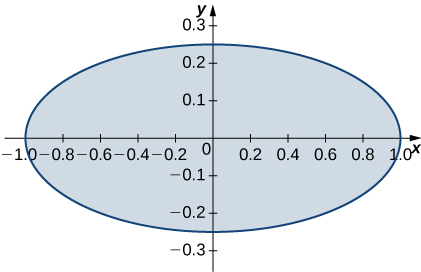
- Answer
- \(\frac{\pi}{2}\)
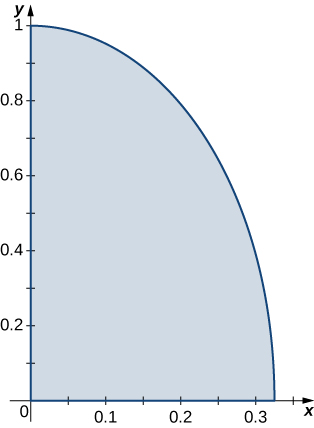
10. \(R = \big\{(x,y) \,|\, 9x^2 + y^2 \leq 1, \space x \geq 0, \space y \geq 0\big\} ; \space \rho (x,y) = \sqrt{9x^2 + y^2}\).
11. \(R\) is the region bounded by \(y = x, \space y = -x, \space y = x + 2, \space y = -x + 2; \space \rho(x,y) = 1\).
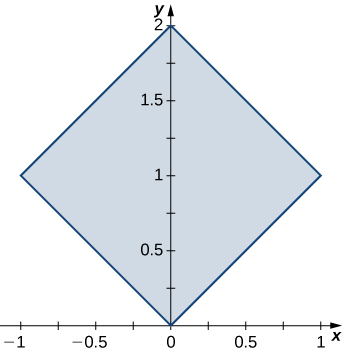
- Answer
- \(2\)
12. \(R\) is the region bounded by \(y = \frac{1}{x}, \space y = \frac{2}{x}, \space y = 1\), and \(y = 2; \space \rho (x,y) = 4(x + y)\).
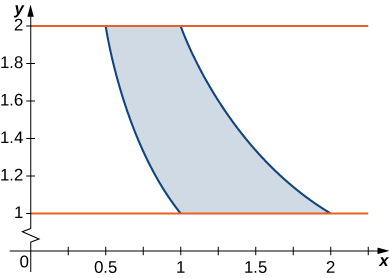
In exercises 13 - 24, consider a lamina occupying the region \(R\) and having the density function \(\rho\) given in the preceding group of exercises. Use a computer algebra system (CAS) to answer the following questions.
a. Find the moments \(M_x\) and \(M_y\) about the \(x\)-axis and \(y\)-axis, respectively.
b. Calculate and plot the center of mass of the lamina.
c. [T] Use a CAS to locate the center of mass on the graph of \(R\).
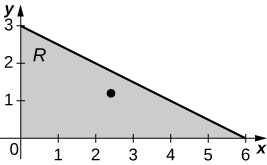
13. [T] \(R\) is the triangular region with vertices \((0,0), \space (0,3)\), and \((6,0); \space \rho (x,y) = xy\).
- Answer
-
a. \(M_x = \frac{81}{5}, \space M_y = \frac{162}{5}\);
b. \(\bar{x} = \frac{12}{5}, \space \bar{y} = \frac{6}{5}\);
c.
14. [T] \(R\) is the triangular region with vertices \((0,0), \space (1,1)\), and \((0,5); \space \rho (x,y) = x + y\).
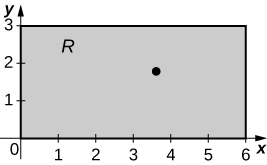
15. [T] \(R\) is the rectangular region with vertices \((0,0), \space (0,3), \space (6,3)\), and \((6,0); \space \rho (x,y) = \sqrt{xy}\).
- Answer
-
a. \(M_x = \frac{216\sqrt{2}}{5}, \space M_y = \frac{432\sqrt{2}}{5}\);
b. \(\bar{x} = \frac{18}{5}, \space \bar{y} = \frac{9}{5}\);
c.
16. [T] \(R\) is the rectangular region with vertices \((0,1), \space (0,3), \space (3,3)\), and \((3,1); \space \rho (x,y) = x^2y\).
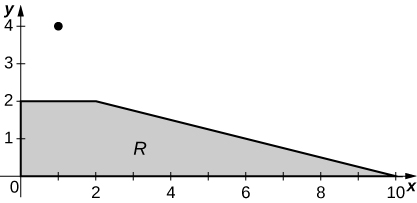
17. [T] \(R\) is the trapezoidal region determined by the lines \(y = - \frac{1}{4}x + \frac{5}{2}, \space y = 0, \space y = 2\), and \(x = 0; \space \rho (x,y) = 3xy\).
- Answer
-
a. \(M_x = \frac{368}{5}, \space M_y = \frac{1552}{5}\);
b. \(\bar{x} = \frac{92}{95}, \space \bar{y} = \frac{388}{95}\);
c.
18. [T] \(R\) is the trapezoidal region determined by the lines \(y = 0, \space y = 1, \space y = x,\) and \(y = -x + 3; \space \rho (x,y) = 2x + y\).
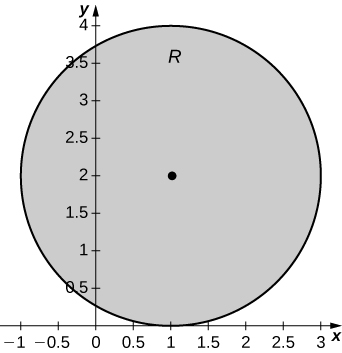
19. [T] \(R\) is the disk of radius \(2\) centered at \((1,2); \space \rho(x,y) = x^2 + y^2 - 2x - 4y + 5\).
- Answer
-
a. \(M_x = 16\pi, \space M_y = 8\pi\);
b. \(\bar{x} = 1, \space \bar{y} = 2\);
c.
20. [T] \(R\) is the unit disk; \(\rho (x,y) = 3x^4 + 6x^2y^2 + 3y^4\).
21. [T] \(R\) is the region enclosed by the ellipse \(x^2 + 4y^2 = 1; \space \rho(x,y) = 1\).
- Answer
-
a. \(M_x = 0, \space M_y = 0)\);
b. \(\bar{x} = 0, \space \bar{y} = 0\);
c.
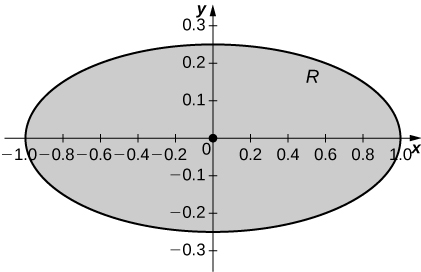
22. [T] \(R = \big\{(x,y) \,|\, 9x^2 + y^2 \leq 1, \space x \geq 0, \space y \geq 0\big\} ; \space \rho (x,y) = \sqrt{9x^2 + y^2}\).
23. [T] \(R\) is the region bounded by \(y = x, \space y = -x, \space y = x + 2\), and \(y = -x + 2; \space \rho (x,y) = 1\).
- Answer
-
a. \(M_x = 2, \space M_y = 0)\);
b. \(\bar{x} = 0, \space \bar{y} = 1\);
c.
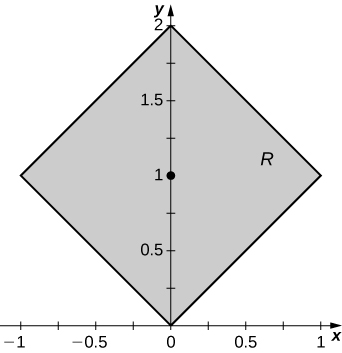
24. [T] \(R\) is the region bounded by \(y = \frac{1}{x}, \space y = \frac{2}{x}, \space y = 1\), and \(y = 2; \space \rho (x,y) = 4(x + y)\).
In exercises 25 - 36, consider a lamina occupying the region \(R\) and having the density function \(\rho\) given in the first two groups of Exercises.
a. Find the moments of inertia \(I_x\), \(I_y\) and \(I_0\) about the \(x\)-axis, \(y\)-axis, and origin, respectively.
b. Find the radii of gyration with respect to the \(x\)-axis, \(y\)-axis, and origin, respectively.
25. \(R\) is the triangular region with vertices \((0,0), \space (0,3)\), and \((6,0); \space \rho (x,y) = xy\).
- Answer
- a. \(I_x = \frac{243}{10}, \space I_y = \frac{486}{5}\), and \(I_0 = \frac{243}{2}\);
b. \(R_x = \frac{3\sqrt{5}}{5}, \space R_y = \frac{6\sqrt{5}}{5}\), and \(R_0 = 3\)
26. \(R\) is the triangular region with vertices \((0,0), \space (1,1)\), and \((0,5); \space \rho (x,y) = x + y\).
27. \(R\) is the rectangular region with vertices \((0,0), \space (0,3), \space (6,3)\), and \((6,0); \space \rho (x,y) = \sqrt{xy}\).
- Answer
- a. \(I_x = \frac{2592\sqrt{2}}{7}, \space I_y = \frac{648\sqrt{2}}{7}\), and \(I_0 = \frac{3240\sqrt{2}}{7}\);
b. \(R_x = \frac{6\sqrt{21}}{7}, \space R_y = \frac{3\sqrt{21}}{7}\), and \(R_0 = \frac{3\sqrt{106}}{7}\)
28. \(R\) is the rectangular region with vertices \((0,1), \space (0,3), \space (3,3)\), and \((3,1); \space \rho (x,y) = x^2y\).
29. \(R\) is the trapezoidal region determined by the lines \(y = - \frac{1}{4}x + \frac{5}{2}, \space y = 0, \space y = 2\), and x = 0; \space \rho (x,y) = 3xy\).
- Answer
- a. \(I_x = 88, \space I_y = 1560\), and \(I_0 = 1648\);
b. \(R_x = \frac{\sqrt{418}}{19}, \space R_y = \frac{\sqrt{7410}}{10}\), and \(R_0 = \frac{2\sqrt{1957}}{19}\)
30. \(R\) is the trapezoidal region determined by the lines \(y = 0, \space y = 1, \space y = x\), and y = -x + 3; \space \rho (x,y) = 2x + y\).
31. \(R\) is the disk of radius \(2\) centered at \((1,2); \space \rho(x,y) = x^2 + y^2 - 2x - 4y + 5\).
- Answer
- a. \(I_x = \frac{128\pi}{3}, \space I_y = \frac{56\pi}{3}\), and \(I_0 = \frac{184\pi}{3}\);
b. \(R_x = \frac{4\sqrt{3}}{3}, \space R_y = \frac{\sqrt{21}}{2}\), and \(R_0 = \frac{\sqrt{69}}{3}\)
32. \(R\) is the unit disk; \(\rho (x,y) = 3x^4 + 6x^2y^2 + 3y^4\).
33. \(R\) is the region enclosed by the ellipse \(x^2 + 4y^2 = 1; \space \rho(x,y) = 1\).
- Answer
- a. \(I_x = \frac{\pi}{32}, \space I_y = \frac{\pi}{8}\), and \(I_0 = \frac{5\pi}{32}\);
b. \(R_x = \frac{1}{4}, \space R_y = \frac{1}{2}\), and \(R_0 = \frac{\sqrt{5}}{4}\)
34. \(R = \big\{(x,y) \,|\, 9x^2 + y^2 \leq 1, \space x \geq 0, \space y \geq 0\big\} ; \space \rho (x,y) = \sqrt{9x^2 + y^2}\).
35. \(R\) is the region bounded by \(y = x, \space y = -x, \space y = x + 2\), and \(y = -x + 2; \space \rho (x,y) = 1\).
- Answer
- a. \(I_x = \frac{7}{3}, \space I_y = \frac{1}{3}\), and \(I_0 = \frac{8}{3}\);
b. \(R_x = \frac{\sqrt{42}}{6}, \space R_y = \frac{\sqrt{6}}{6}\), and \(R_0 = \frac{2\sqrt{3}}{3}\)
36. \(R\) is the region bounded by \(y = \frac{1}{x}, \space y = \frac{2}{x}, \space y = 1\), and \(y = 2; \space \rho (x,y) = 4(x + y)\).
37. Let \(Q\) be the solid unit cube. Find the mass of the solid if its density \(\rho\) is equal to the square of the distance of an arbitrary point of \(Q\) to the \(xy\)-plane.
- Answer
- \(m = \frac{1}{3}\)
38. Let \(Q\) be the solid unit hemisphere. Find the mass of the solid if its density \(\rho\) is proportional to the distance of an arbitrary point of \(Q\) to the origin.
39. The solid \(Q\) of constant density \(1\) is situated inside the sphere \(x^2 + y^2 + z^2 = 16\) and outside the sphere \(x^2 + y^2 + z^2 = 1\). Show that the center of mass of the solid is not located within the solid.
40. Find the mass of the solid \(Q = \big\{ (x,y,z) \,|\, 1 \leq x^2 + z^2 \leq 25, \space y \leq 1 - x^2 - z^2 \big\}\) whose density is \(\rho (x,y,z) = k\), where \(k > 0\).
41. [T] The solid \(Q = \big\{ (x,y,z) \,|\, x^2 + y^2 \leq 9, \space 0 \leq z \leq 1, \space x \geq 0, \space y \geq 0\big\}\) has density equal to the distance to the \(xy\)-plane. Use a CAS to answer the following questions.
a. Find the mass of \(Q\).
b. Find the moments \(M_{xy}, \space M_{xz}\) and \(M_{yz}\) about the \(xy\)-plane, \(xz\)-plane, and \(yz\)-plane, respectively.
c. Find the center of mass of \(Q\).
d. Graph \(Q\) and locate its center of mass.
- Answer
-
a. \(m = \frac{9\pi}{4}\);
b. \(M_{xy} = \frac{3\pi}{2}, \space M_{xz} = \frac{81}{8}, \space M_{yz} = \frac{81}{8}\);
c. \(\bar{x} = \frac{9}{2\pi}, \space \bar{y} = \frac{9}{2\pi}, \space \bar{z} = \frac{2}{3}\);
d.
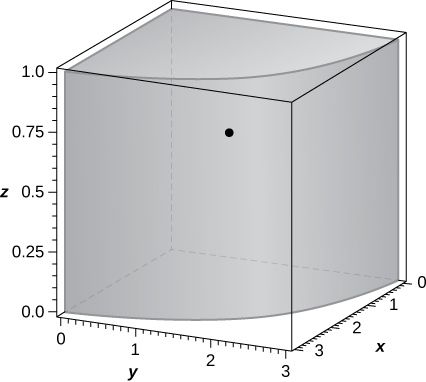
42. Consider the solid \(Q = \big\{ (x,y,z) \,|\, 0 \leq x \leq 1, \space 0 \leq y \leq 2, \space 0 \leq z \leq 3\big\}\) with the density function \(\rho(x,y,z) = x + y + 1\).
a. Find the mass of \(Q\).
b. Find the moments \(M_{xy}, \space M_{xz}\) and \(M_{yz}\) about the \(xy\)-plane, \(xz\)-plane, and \(yz\)-plane, respectively.
c. Find the center of mass of \(Q\).
43. [T] The solid \(Q\) has the mass given by the triple integral \(\displaystyle \int_{-1}^1 \int_0^{\pi/4} \int_0^1 r^2 \, dr \space d\theta \space dz.\)
Use a CAS to answer the following questions.
- Show that the center of mass of \(Q\) is located in the \(xy\)-plane.
- Graph \(Q\) and locate its center of mass.
- Answer
-
\(\bar{x} = \frac{3\sqrt{2}}{2\pi}\), \(\bar{y} = \frac{3(2-\sqrt{2})}{2\pi}, \space \bar{z} = 0\); 2. the solid \(Q\) and its center of mass are shown in the following figure.
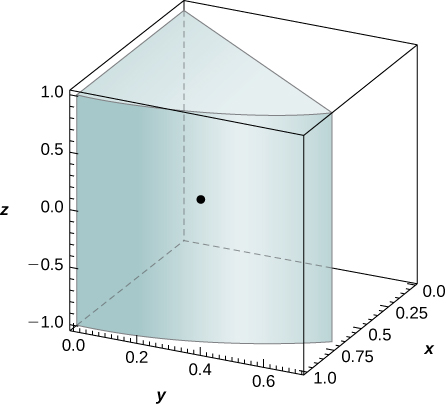
44. The solid \(Q\) is bounded by the planes \(x + 4y + z = 8, \space x = 0, \space y = 0\), and \(z = 0\). Its density at any point is equal to the distance to the \(xz\)-plane. Find the moments of inertia of the solid about the \(xz\)-plane.
45. The solid \(Q\) is bounded by the planes \(x + y + z = 3, \space x = 0, \space y = 0\), and \(z = 0\). Its density is \(\rho(x,y,z) = x + ay\), where \(a > 0\). Show that the center of mass of the solid is located in the plane \(z = \frac{3}{5}\) for any value of \(a\).
46. Let \(Q\) be the solid situated outside the sphere \(x^2 + y^2 + z^2 = z\) and inside the upper hemisphere \(x^2 + y^2 + z^2 = R^2\), where \(R > 1\). If the density of the solid is \(\rho (x,y,z) = \frac{1}{\sqrt{x^2+y^2+z^2}}\), find \(R\) such that the mass of the solid is \(\frac{7\pi}{2}.\)
47. The mass of a solid \(Q\) is given by \(\displaystyle \int_0^2 \int_0^{\sqrt{4-x^2}} \int_{\sqrt{x^2+y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2)^n \, dz \space dy \space dx,\) where \(n\) is an integer. Determine \(n\) such the mass of the solid is \((2 - \sqrt{2}) \pi\).
- Answer
- \(n = -2\)
48. Let \(Q\) be the solid bounded above the cone \(x^2 + y^2 = z^2\) and below the sphere \(x^2 + y^2 + z^2 - 4z = 0\). Its density is a constant \(k > 0\). Find \(k\) such that the center of mass of the solid is situated \(7\) units from the origin.
49. The solid \(Q = \big\{(x,y,z) \,|\, 0 \leq x^2 + y^2 \leq 16, \space x \geq 0, \space y \geq 0, \space 0 \leq z \leq x\big\}\) has the density \(\rho (x,y,z) = k\). Show that the moment \(M_{xy}\) about the \(xy\)-plane is half of the moment \(M_{yz}\) about the \(yz\)-plane.
50. The solid \(Q\) is bounded by the cylinder \(x^2 + y^2 = a^2\), the paraboloid \(b^2 - z = x^2 + y^2\), and the \(xy\)-plane, where \(0 < a < b\). Find the mass of the solid if its density is given by \(\rho(x,y,z) = \sqrt{x^2 + y^2}\).
51. Let \(Q\) be a solid of constant density \(k\), where \(k > 0\), that is located in the first octant, inside the circular cone \(x^2 + y^2 = 9(z - 1)^2\), and above the plane \(z = 0\). Show that the moment \(M_{xy}\) about the \(xy\)-plane is the same as the moment \(M_{yz}\) about the \(xz\)-plane.
52. The solid \(Q\) has the mass given by the triple integral \(\displaystyle \int_0^1 \int_0^{\pi/2} \int_0^{r^3} (r^4 + r) \space dz \space d\theta \space dr.\)
a. Find the density of the solid in rectangular coordinates.
b. Find the moment \(M_{xy}\) about the \(xy\)-plane.
53. The solid \(Q\) has the moment of inertia \(I_x\) about the \(yz\)-plane given by the triple integral \(\displaystyle \int_0^2 \int_{-\sqrt{4-y^2}}^{\sqrt{4-y^2}} \int_{\frac{1}{2}(x^2+y^2)}^{\sqrt{x^2+y^2}} (y^2 + z^2)(x^2 + y^2) \, dz \space dx \space dy.\)
a. Find the density of \(Q\).
b. Find the moment of inertia \(I_z\) about the \(xy\)-plane.
- Answer
- a. \(\rho (x,y,z) = x^2 + y^2\);
b. \(\frac{16\pi}{7}\)
54. The solid \(Q\) has the mass given by the triple integral \(\displaystyle \int_0^{\pi/4} \int_0^{2 \space sec \space \theta} \int_0^1 (r^3 \cos \theta \sin \theta + 2r) \, dz \space dr \space d\theta.\)
a. Find the density of the solid in rectangular coordinates.
b. Find the moment \(M_{xz}\) about the \(xz\)-plane.
55. Let \(Q\) be the solid bounded by the \(xy\)-plane, the cylinder \(x^2 + y^2 = a^2\), and the plane \(z = 1\), where \(a > 1\) is a real number. Find the moment \(M_{xy}\) of the solid about the \(xy\)-plane if its density given in cylindrical coordinates is \(\rho(x,y,z) = \frac{d^2f}{dr^2} (r)\), where \(f\) is a differentiable function with the first and second derivatives continuous and differentiable on \((0,a)\).
- Answer
- \(M_{xy} = \pi (f(0) - f(a) + af'(a))\)
56. A solid \(Q\) has a volume given by \(\displaystyle \iint_D \int_a^b \, dA \space dz\), where \(D\) is the projection of the solid onto the \(xy\)-plane and \(a < b\) are real numbers, and its density does not depend on the variable \(z\). Show that its center of mass lies in the plane \(z = \frac{a+b}{2}\).
57. Consider the solid enclosed by the cylinder \(x^2 + z^2 = a^2\) and the planes \(y = b\) and \(y = c\), where \(a > 0\) and \(b < c\) are real numbers. The density of \(Q\) is given by \(\rho(x,y,z) = f'(y)\), where \(f\) is a differential function whose derivative is continuous on \((b,c)\). Show that if \(f(b) = f(c)\), then the moment of inertia about the \(xz\)-plane of \(Q\) is null.
58. [T] The average density of a solid \(Q\) is defined as \( \displaystyle \rho_{ave} = \frac{1}{V(Q)} \iiint_Q \rho(x,y,z) \, dV = \frac{m}{V(Q)},\) where \(V(Q)\) and \(m\) are the volume and the mass of \(Q\), respectively. If the density of the unit ball centered at the origin is \(\rho (x,y,z) = e^{-x^2-y^2-z^2}\), use a CAS to find its average density. Round your answer to three decimal places.
59. Show that the moments of inertia \(I_x, \space I_y\), and \(I_z\) about the \(yz\)-plane, \(xz\)-plane, and \(xy\)-plane, respectively, of the unit ball centered at the origin whose density is \(\rho (x,y,z) = e^{-x^2-y^2-z^2}\) are the same. Round your answer to two decimal places.
- Answer
- \(I_x = I_y = I_z \approx 0.84\)
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.






















