4.2: Subsets and Power Sets
- Page ID
- 23270
We usually consider sets containing elements of similar types. The collection of all the objects under consideration is called the universal set, and is denoted \({\cal U}\). For example, for numbers, the default universal set is \(\mathbb{R}\).
Venn Diagrams
Example \(\PageIndex{1}\label{eg:subsets-geomfig}\)
Venn diagrams are useful in demonstrating set relationship. Let \[\begin{aligned} {\cal U} &=& \mbox{set of geometric figures}, \\ S &=& \mbox{set of squares}, \\ P &=& \mbox{set of parallelogram}, \\ R &=& \mbox{set of rhombuses}, \\ L &=& \mbox{set of rectangles}, \\ C &=& \mbox{set of circles}. \end{aligned}\] Their relationship is displayed in the figure below.
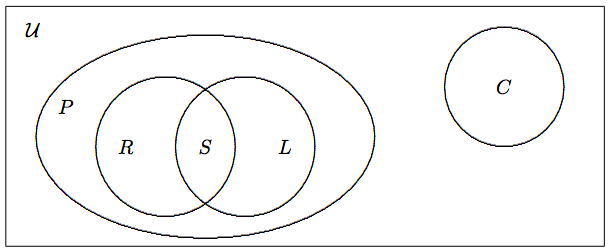 Figure \(\PageIndex{1}\): The relationship among various sets of geometric figures.
Figure \(\PageIndex{1}\): The relationship among various sets of geometric figures.
The pictorial representation in the figure above is called a Venn diagram. We use a rectangle to represent the universal set, and circles or ovals to represent the sets inside the universal set. The relative positions of these circles and ovals indicate the relationship of the respective sets. For example, having \(R\), \(S\), and \(L\) inside \(P\) means that rhombuses, squares, and rectangles are parallelograms. In contrast, circles are incomparable to parallelograms.
Definition: Subset
Set \(A\) is a subset of set \(B\), denoted by \(A \subseteq B\), if every element of \(A\) is also an element of \(B\). See Figure (figure not here yet).
Symbolicly:
\(A \subseteq B\) if and only if \(x \in A \rightarrow x \in B.\)
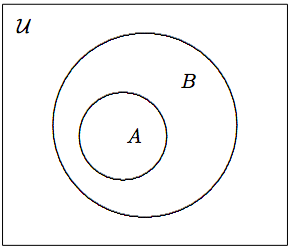 Figure \(\PageIndex{2}\): The Venn diagram for \(A \subseteq B\).
Figure \(\PageIndex{2}\): The Venn diagram for \(A \subseteq B\).
In some texts, you may see this notation: \(B\) is a superset of \(A\), and write \(B \supseteq A\), which is similar to \(y\geq x\).
Example \(\PageIndex{2}\label{eg:subsets-02}\)
It is clear that \(\mathbb{N}\subseteq\mathbb{Z}\) and \(\mathbb{Z}\subseteq\mathbb{R}\). We can nest these two relationships into one, and write \(\mathbb{N}\subseteq\mathbb{Z} \subseteq\mathbb{R}\). More generally, we have \[\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} \subseteq \mathbb{R}.\] Compare this to \(x \leq y \leq z \leq w\). We shall discover many similarities between \(\subseteq\) and \(\leq\).
Example \(\PageIndex{3}\label{eg:subsets-03}\)
It is obvious that \[\{1,2,7\} \subseteq \{1,2,3,6,7,9\}\] because all three elements 1, 2, and 7 from the set on the left also appear as elements in the set on the right. Meanwhile, \[\{1,2,7\} \nsubseteq \{1,2,3,6,8,9\}\] because 7 belongs to the first set but not the second.
Example \(\PageIndex{4}\label{eg:subsets-04}\)
The following statements are true:
- \(\{1,2,3\}\subseteq \mathbb{N}\).
- \(\{x\in\mathbb{R} \mid x^2=1\} \subseteq \mathbb{Z}\).
Be sure you can explain clearly why these subset relationships hold.
hands-on exercise \(\PageIndex{1}\label{he:subsets-01}\)
Are these statements true or false?
- \(\{-1,2\} \nsubseteq \mathbb{N}\), and \(\{-1,2\} \subseteq \mathbb{Z}\).
- \(\{x\in\mathbb{Z} \mid x^2\leq1\} \subseteq \mathbb{R}\).
Example \(\PageIndex{5}\label{eg:subsets-05}\)
Do not assume that if \(A\nsubseteq B\) then we must have \(B\subseteq A\). For instance, if \(A=\{1,5,7\}\) and \(B=\{3,8\}\), then \(A \nsubseteq B\); but we also have \(B \nsubseteq A\).
The last example demonstrates that \(A\nsubseteq B\) is more complicated than just changing the subset notation as we do with inequalities. We need a more precise definition of the subset relationship:
\[A \subseteq B \Leftrightarrow
\forall x\in{\cal U} \,(x \in A \Rightarrow x \in B)\]
It follows that \[A \nsubseteq B \Leftrightarrow \exists x\in{\cal U} \,(x \in A \wedge x \not\in B). \nonumber\] Hence, to show that \(A\) is not a subset of \(B\), we need to find an element \(x\) that belongs to \(A\) but not \(B\). There are three possibilities; their Venn diagrams are depicted in Figure \(\PageIndex{3}\).
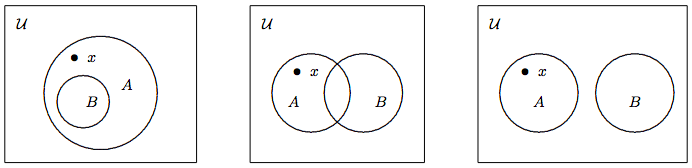
Example \(\PageIndex{6}\label{eg:subsets-06}\)
We have \([3,6]\subseteq[2,7)\), and \([3,6]\nsubseteq[4,7)\). We also have \((3,4) \subseteq [3,4]\).
hands-on exercise \(\PageIndex{2}\label{he:subsets-02}\)
True or false: \([3,4) \subseteq (3,4)\)? Explain.
To prove \(S \subseteq T\)
To prove a set is a subset of another set, follow these steps.
(1) Let \(x\) be an arbitrary element of set \(S\).
(2) Show \(x\) is an element of set \(T\).
This proves every element of set \(S\) is an element of \(T\).
Example:
Prove \(\mathbb{Z} \subseteq \mathbb{Q}.\)
Let \(x \in \mathbb{Z}.\)
\(x=\frac{x}{1}.\)
See if you can continue this proof.
- Continuation of Proof
-
Since \(x \in \mathbb{Z}\) and \(1 \in \mathbb{Z}\) and \(1 \neq 0,\)
\(\frac{x}{1} \in \mathbb{Q},\) by definition of rational numbers.Thus \(x \in \mathbb{Q},\) by substitution.
\(\therefore \mathbb{Z} \subseteq \mathbb{Q}.\)
With the notion of universal set, we can now refine the definition for set equality; here's our original definition:
\[A = B \Leftrightarrow
\forall x\in{\cal U}\,(x\in A \Leftrightarrow x\in B)\]
Logically, \(x\in A \Leftrightarrow x\in B\) is equivalent to \[(x\in A \Rightarrow x\in B) \wedge (x\in B\Rightarrow x\in A).\] Therefore, we can also define the equality of sets via subset relationship:
Equality of Sets: Subset Definition
\[A = B \Leftrightarrow
(A \subseteq B) \wedge (B \subseteq A)\]
which can be compared to \[x=y \Leftrightarrow (x\leq y) \wedge (y\leq x)\] for real numbers \(x\) and \(y\).
This new definition of set equality suggests that in order to prove that \(A=B\), we could use this two-step argument.
To Prove Sets Equal
(1) Show that \(A \subseteq B\).
(2) Show that \(B \subseteq A\).
.
This technique is useful when it is impossible or impractical to list the elements of \(A\) and \(B\) for comparison. This is particularly true when \(A\) and \(B\) are defined abstractly. We will apply this technique in the coming sections.
The two relationship \(\subseteq\) and \(\leq\) share many common properties. The transitive property is another example.
Theorem \(\PageIndex{1}\) Transitivity of Subsets
Let \(A\), \(B\), and \(C\) be sets. If \(A\subseteq B\) and \(B\subseteq C\), then \(A\subseteq C\).
Discussion
The theorem statement is in the form of an implication. To prove \(p\Rightarrow q\), we start with the assumption \(p\), and use it to show that \(q\) must also be true. In this case, these two steps become
- Assume that \(A\subseteq B\) and \(B\subseteq C\).
- Show that \(A\subseteq C\).
How can we prove that \(A\subseteq C\)? We know that \(A\subseteq C\) means \[\forall x\in{\cal U}\,(x\in A\Rightarrow x\in C).\] So we have to start with \(x\in A\), and attempt to show that \(x\in C\) as well. How can we show that \(x\in C\)? We need to use the assumption \(A\subseteq B\) and \(B\subseteq C\).
- Proof
-
Assume \(A\subseteq B\) and \(B\subseteq C\).
Let \(x\in A\). Since \(A\subseteq B\), \(x\in B\) by definition of subset.
Likewise, since \(B\subseteq C\), \(x\in C,\) by definition of subset.
Thus \(\forall x\in{\cal U}\,(x\in A\Rightarrow x\in C).\)
So we conclude that \(A\subseteq C\) by definition of subset.\(\therefore \) if \(A\subseteq B\) and \(B\subseteq C\), then \(A\subseteq C\).
The proof relies on the definition of the subset relationship. Many proofs in mathematics are rather simple if you know the underlying definitions.
Example \(\PageIndex{7}\) A Biconditional Proof
Prove that \(x \in A \Leftrightarrow \{x\} \subseteq A\), for any element \(x\in{\cal U}\)
Discussion
We call \(p\Leftrightarrow q\) a biconditional statement because it consists of two implications \(p \Rightarrow q\) and \(p\Leftarrow q\). Hence, we need to prove it in two steps:
- Show that \(p \Rightarrow q\).
- Show that \(q \Rightarrow p\).
We call these two implications the necessity and sufficiency of the biconditional statement, and denote them (\(\Rightarrow\)) and (\(\Leftarrow\)), respectively. In this problem,
- (\(\Rightarrow\)) means “\(x\in A\Rightarrow\{x\}\subseteq A\)”.
- (\(\Leftarrow\)) means “\(\{x\}\subseteq A\Rightarrow x\in A\)”.
This is a sketch of how the proof may look:
\((\Rightarrow)\quad \) Assume \(x\in A. \qquad\ldots\qquad\) Therefore \(\{x\}\subseteq A\).
\((\Leftarrow)\quad\) Assume \(\{x\} \subseteq A. \qquad\ldots\qquad\) Therefore \(x\in A\).
We now proceed to finish the proof.
- Answer
-
(\(\Rightarrow\)) Assume \(x \in A\). The set \(\{x\}\) contains only one element \(x\), which is also an element of \(A\). Thus, every element of \(\{x\}\) is also an element of \(A\). By definition of subset, \(\{x\} \subseteq A\).
(\(\Leftarrow\)) Assume \(\{x\} \subseteq A\). The definition of the subset asserts that every element of \(\{x\}\) is also an element of \(A\). In particular, \(x\) is an element of \(\{x\}\), so by definition of subset, it is also an element of \(A\). Thus, \(x \in A\).
Definition - Proper subset
The set \(A\) is a proper subset of \(B\), denoted \(A \subset B\), if \(A\) is a subset of \(B\), and \(A\neq B\). Symbolically, \(A \subset B \Leftrightarrow (A \subseteq B) \wedge (A \neq B)\). Equivalently, \[A \subset B \Leftrightarrow (A \subseteq B) \wedge \exists x\in{\cal U}\,(x \in B \wedge x \not\in A).\] See the Venn diagram in Figure \(\PageIndex{4}\).
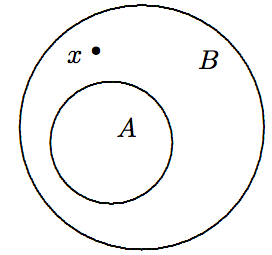 Figure \(\PageIndex{4}\): The definition of a proper subset.
Figure \(\PageIndex{4}\): The definition of a proper subset.
Example \(\PageIndex{8}\label{eg:subsets-08}\)
It is clear that \([0,5]\subset\mathbb{R}\). We also have \[\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}.\] Note the similarities between \(\subset\) and \(<\). Compare the last expression to \[x < y < z < w.\] Here is another similarity between \(\subset\) and \(<\). For numbers, \(x<y\) and \(y<z\) together imply that \(x<z\). This is the transitive property. In a similar fashion, for sets, if \(A\subset B\) and \(B\subset C\), then \(A\subset C\); the transitive property holds for proper subsets.
hands-on exercise \(\PageIndex{3}\label{he:subsets-03}\)
True or false: \((3,4)\subset[3,4]\)? How about \((3,4)\subset(3,4]\)?
Empty Set Theorems
Theorem \(\PageIndex{2}\) \(\emptyset\) is a Subset of Every Set
For any set \(A\), we have \(\emptyset \subseteq A\) and \(A \subseteq A\). In particular, \(\emptyset\subseteq\emptyset\).
- Proof
-
Since every element of \(A\) also appears in \(A\), it follows immediately that \(A\subseteq A\). To show that \(\emptyset\subseteq A\), we need to verify the implication \[x\in\emptyset \Rightarrow x\in A\] for any arbitrary \(x\in{\cal U}\). Since \(\emptyset\) is empty, \(x\in\emptyset\) is always false; hence, the implication is always true. Consequently, \(\emptyset\subseteq A\) for any set \(A\). In particular, when \(A=\emptyset\), we obtain \(\emptyset\subseteq \emptyset\).
Theorem \(\PageIndex{3}\) The \(\emptyset \) is Unique
An empty set is defined as a set with no elements. We want to show there is just one empty set; only one set that has no elements. Then we can refer to it as "the" empty set.
- Proof
-
Suppose \(E_1\) and \(E_2\) are empty sets, that is, they each have no elements. From Theorem 4.2.2, since \(E_1\) has no elements, \(E_1 \subseteq E_2.\) By the same reasoning, \(E_2 \subseteq E_1.\) Now from the definition of equality, \(E_2 = E_1.\) Thus there is just one empty set.
Example \(\PageIndex{9}\label{eg:subsets-09}\)
Determine the truth values of these expressions.
(a) \(\emptyset \in \emptyset\) & (b) \(1 \subseteq \{1\}\) & (c) \(\emptyset \in \{\emptyset\}\)
- Answer
-
(a) By definition, an empty set contains no element. Consequently, the statement \(\emptyset\in\emptyset\) is false.
(b) A subset relation only exists between two sets. To the left of the symbol \(\subseteq\), we have only a number, which is not a set. Hence, the statement is false. In fact, this expression is syntactically incorrect.
(c) The set \(\{\emptyset\}\) contains one element, which happens to be an empty set. Compare this to an empty box inside another box. The outer box is described by the pair of set brackets \(\{\,\ldots\,\}\), and the (empty) box inside is \(\emptyset\). It follows that \(\emptyset\in\{\emptyset\}\) is a true statement.
hands-on exercise \(\PageIndex{4}\label{he:subsets-04}\)
Determine the truth values of these expressions.
(a) \(\emptyset \subseteq \{\emptyset\}\) & (b) \(\{1\} \subseteq \big\{1,\{1,2\}\big\}\) & (c) \(\{1\} \subseteq \big\{\{1\},\{1,2\}\big\}\)
Definition-Power Set
The set of all subsets of \(A\) is called the power set of \(A\), denoted \(\mathscr{P}(A).\)
Since a power set itself is a set, we need to use a pair of left and right curly braces (set brackets) to enclose all its elements. Its elements are themselves sets, each of which requires its own pair of left and right curly braces. Consequently, we need at least two levels of set brackets to describe a power set.
Example \(\PageIndex{10}\) Examples of Power Sets
Let \(A=\{1,2\}\) and \(B=\{1\}\). The subsets of \(A\) are \(\emptyset\), \(\{1\}\), \(\{2\}\) and \(\{1,2\}\). Therefore, \[\mathscr{P}(A) = \big\{\emptyset, \{1\},\{2\},\{1,2\} \big\}.\]
In a similar manner, we find \[\mathscr{P}(B) = \big\{ \emptyset, \{1\} \big\}.\]
We can write directly \[\mathscr{P}(\{1,2\}) = \big\{ \emptyset, \{1\}, \{2\}, \{1,2\} \big\}, \qquad\mbox{and}\qquad\mathscr{P}(\{1\}) = \big\{ \emptyset, \{1\} \big\}\]
without introducing letters to represent the sets involved.
hands-on exercise \(\PageIndex{5}\label{he:subsets-05}\)
Let us evaluate \(\mathscr{P}(\{1,2,3,4\})\). To ensure that no subset is missed, we list these subsets according to their sizes. Since \(\emptyset\) is the subset of any set, \(\emptyset\) is always an element in the power set. This is the subset of size 0. Next, list the singleton subsets (subsets with only one element). Then the doubleton subsets, and so forth. Complete the following table.
\[\begin{array}{|c|l|} \hline \mbox{size} & \mbox{subsets} \\ \hline 0 & \emptyset \\ 1 & \{1\}, \{2\}, \ldots \qquad \\ 2 & \{1,2\}, \{1,3\}, \ldots \hskip2in \\ 3 & \{1,2,3\}, \ldots \hskip1in \\ 4 & \ldots \\ \hline \end{array}\] Since \(A\subseteq A\) for any set \(A\), the power set \(\mathscr{P}(A)\) always contains \(A\) itself. As a result, the last subset in the list should be \(A\) itself.
We are now ready to put them together to form the power set. All you need is to put all the subsets inside a pair of bigger curly braces (a power set is itself a set; hence, it needs a pair of curly braces in its description). Put your final answer in the space below.
Check to make sure that the left and right braces match perfectly.
Example \(\PageIndex{11}\label{eg:subsets-11}\)
Since \(A\) is a subset of \(A\), it belongs to \(\mathscr{P}(A)\). Nonetheless, it is improper to say \(A \subseteq \mathscr{P}(A)\). Can you explain why? What should be the correct notation?
- Answer
-
The power set \(\mathscr{P}(A)\) is the collection of all the subsets of \(A\). Thus, the elements in \(\mathscr{P}(A)\) are subsets of \(A\). One of these subsets is the set \(A\) itself. Hence, \(A\) itself appears as an element in \(\wp(A)\), and we write \(A\in\wp(A)\) to describe this membership.
This is different from saying that \(A\subseteq\mathscr{P}(A)\). In order to have the subset relationship \(A\subseteq\mathscr{P}(A)\), every element in \(A\) must also appear as an element in \(\mathscr{P}(A)\). The elements of \(\mathscr{P}(A)\) are sets (they are subsets of \(A\), and subsets are sets). An element of \(A\) is not the same as a subset of \(A\). Therefore, although \(A\subseteq\mathscr{P}(A)\) is syntactically correct, its truth value is false.
hands-on exercise \(\PageIndex{6}\label{he:subsets-06}\)
Explain the difference between \(\emptyset\) and \(\{\emptyset\}\). How many elements are there in \(\emptyset\) and \(\{\emptyset\}\)? Is it true that \(\mathscr{P}(\emptyset) = \{\emptyset\}\)?
Theorem \(\PageIndex{3}\) \(2^n\) subsets for a set with \(n\) elements.
If \(A\) is an \(n\)-element set, then \(\mathscr{P}(A)\) has \(2^n\) elements. In other words, an \(n\)-element set has \(2^n\) distinct subsets.
- Proof
-
How many subsets of \(A\) can we construct? To form a subset, we go through each of the \(n\) elements and ask ourselves if we want to include this particular element or not. Since there are two choices (yes or no) for each of the \(n\) elements in \(A\), we have found \(\underbrace{2\cdot2\cdot\cdots2}_{\mbox{ n times}}\, =2^n\) subsets.
hands-on exercise \(\PageIndex{7}\label{he:subsets-07}\)
How many elements are there in \(\mathscr{P}(\{\alpha,\beta, \gamma\})\)? What are they?
hands-on exercise \(\PageIndex{8}\label{he:subsets-08}\)
What is the cardinality of \(\emptyset\)? How about \(\mathscr{P}(\emptyset)\)? Describe \(\mathscr{P}(\emptyset)\).
hands-on exercise \(\PageIndex{9}\label{he:subsets-09}\)
Is it correct to write \(|\mathscr{P}(A)|=2^{|A|}\)? How about \(|\mathscr{P}(A)|=2^A\)? Explain.
Example \(\PageIndex{12}\) Complicated Power Sets
When a set contains sets as elements, its power set could become rather complicated. Here are two examples.
\[\begin{aligned}\mathscr{P}(\big\{\{a\},\{1\}\big\}) &=& \Big\{ \emptyset, \big\{\{a\}\big\}, \big\{\{1\}\big\}, \big\{\{a\},\{1\}\big\} \Big\}, \\ \mathscr{P}(\big\{\emptyset,\{1\}\big\}) &=& \Big\{ \emptyset, \{\emptyset\}, \big\{\{1\}\big\}, \big\{\emptyset,\{1\}\big\} \Big\}. \end{aligned}\]
Be sure you understand the notations used in these examples. In particular, examine the number of levels of set brackets used in each example.
Summary and Review
- A set \(S\) is a subset of another set \(T\) if and only if every element in \(S\) can be found in \(T\).
- In symbols, \(S\subseteq T \Leftrightarrow \forall x\in{\cal U}\, (x\in S \Rightarrow x\in T)\).
- Consequently, to show that \(S\subseteq T\), we have to start with an arbitrary element \(x\) in \(S\), and show that \(x\) also belongs to \(T\).
- For sets \(S\) and \(T\), \(S =T \Leftrightarrow (S\subseteq T) \wedge (T \subseteq S)\).
- The definition of subset relationship implies that for any set \(S\), we always have \(\emptyset\subseteq S\) and \(S\subseteq S\).
- The empty set is unique.
- The power set of a set \(S\), denoted \(\wp(S)\), contains all the subsets of \(S\).
- If \(|S|=n\), then \(|\mathscr{P}(S)|=2^n\). Hence, an \(n\)-element set has \(2^n\) subsets.
- To construct \(\mathscr{P}(S)\), list the subsets of \(S\) according to their sizes. Be sure to use a pair of curly braces for each subset, and enclose all of them within a pair of outer curly braces.
Exercises
Exercise \(\PageIndex{1}\label{ex:subsets-01}\)
Determine which of the following statements are true and which are false.
- (a) \(\{1,2,3\} \subseteq \{0,1,2,3,4\}\)
- (b) \(\{1,2,3\} \subseteq \mathbb {N}\)
- (c) \(\{1,2\} \subset [1,2]\)
- (d) \([2,4] \subseteq (0,6)\)
- (e) \([2,4) \subset [2,4]\)
- (f) \([2,4) \subseteq (2,4]\)
- Answer
-
All are true except (f) is false.
Exercise \(\PageIndex{2}\label{ex:subsets-02}\)
Determine which of the following statements are true and which are false.
- (a) \(a \subseteq \{a\}\)
- (b) \(\{a\} \subseteq \{a,b\}\)
- (c) \(\emptyset \subseteq \emptyset\)
- (d) \(\emptyset \subseteq \{\emptyset\}\)
- (e) \(\emptyset \subset \{\emptyset\}\)
- (f) \(\{a\} \subseteq \mathscr{P}(\{\{a\},\{b\}\})\)
Exercise \(\PageIndex{3}\label{ex:subsets-03}\)
True or false: \( 5\mathbb{N} \subseteq \mathbb{N}\)? Explain.
- Answer
-
True. \( 5\mathbb{N}\) contains all the integers that are multiples of 5, and each of these is an integer.
Exercise \(\PageIndex{4}\label{ex:subsets-04}\)
True or false: \(\mathbb{N} \subseteq 6\mathbb{N}\)? Explain.
Exercise \(\PageIndex{5}\)
Determine which of the following statements are true, and which are false. Explain!
- (a) \(\{a\}\in \{a,b,c\}\)
- (b) \(\{a\}\subseteq\{\{a\},b,c\}\)
- (c) \(\{a\}\in \mathscr{P}(\{\{a\},b,c\})\)
- Answer
-
(a) False, because the set \(\{a\}\) cannot be found in \(\{a,b,c\}\) as an element.
(b) False, because \(a\), the sole element in \(\{a\}\), cannot be found in \(\{\{a\},b,c\}\) as an element.
(c) False. For \(\{a\}\in\mathscr{P}(\{\{a\},b,c\})\), the set \(\{a\}\) must be a subset of \(\{\{a\},b,c\}\}\). This means \(a\) must belong to \(\{\{a\},b,c\}\), which is not true.
Exercise \(\PageIndex{6}\label{ex:subsets-06}\)
Determine whether the following statements are true or false:
- (a) The empty set \(\emptyset\) is a subset of \(\{1,2,3\}\).
- (b) If \(A=\{1,2,3\}\), then \(\{1\}\) is a subset of \(\mathscr{P}(A)\).
- (c) \(\emptyset \in \{1,2,3\}\).
Exercise \(\PageIndex{7}\label{ex:subsets-07}\)
Find the power set of the following sets.
- (a) \(\{a,b\}\)
- (b) \(\{4,7\}\)
- (c) \(\{x,y,z,w\}\)
- (d) \(\big\{\{a\}\big\}\)
- (e) \(\big\{ a,\{b\} \big\}\)
- (f) \(\big\{ \{x\},\{y\} \big\}\)
- Answer
-
(e) \(\big\{\emptyset,\{a\},\{\{b\}\},\{a,\{b\}\}\big\}\) .
Exercise \(\PageIndex{8}\label{ex:subsets-08}\)
Evaluate the following sets.
- (a) \(\mathscr{P}(\{\emptyset\})\)
- (b) \(\mathscr{P}(\mathscr{P}(\{a,b\}))\)
- (c) \(\mathscr{P}(\mathscr{P}(\mathscr{P}(\emptyset)))\)
Exercise \(\PageIndex{9}\label{ex:subsets-09}\)
Determine which of the following statements are true, and which are false.
(a) \(\{a\}\subseteq\{a,b,c\}\)
(b) \(\{a\}\subseteq\{\{a,b\},c\}\)
(c) \(\{a\}\in \{a,b,c\}\)
(d) \(\{a\}\in \mathscr{P}(\{a,b,c\})\)
(e) \(\emptyset \in \{a,b,c\}\)
- Answer
-
(a) True (b) False (c) False (d) True (e) False
Exercise \(\PageIndex{10}\label{ex:subsets-10}\)
Let \(P=\{n \in \mathbb{Z} \mid n=3k \mbox{ for some integer }k\}\) and \(Q=\{m \in \mathbb{Z} \mid m=6j-15 \mbox{ for some integer }j\}.\)
(a) Prove \(Q\subseteq P.\)
(b) Explain with a counter example why \(P \nsubseteq Q.\)
Exercise \(\PageIndex{11}\)
Determine which of the following statements are true, and which are false.
(a) \(\mathbb{Z}^+ \in \mathbb{Q}\)
(b) \(\mathbb{Q}^+ \subseteq \mathbb{R}\)
(c) \(\mathbb{Q} \subseteq \mathbb{Z}\)
(d) \(\mathbb{Z}^+ = \mathbb{N}\)
- Answer
-
(a) False (b) True (c) False (d) True
Exercise \(\PageIndex{12}\label{ex:subsets-12}\)
Let \(A=\{n \in \mathbb{Z} \mid n=8k-3 \mbox{ for some integer }k\}\) and \(B=\{m \in \mathbb{Z} \mid m=8j+5 \mbox{ for some integer }j\}.\)
Prove \(A=B.\)
Exercise \(\PageIndex{13}\)
We have learned that \(A\subseteq A\) for any set \(A\).
Which of these is correct: (a) \(A\in\mathscr{P}(A)\) or (b) \(A\subseteq\mathscr{P}(A)\)?
- Answer
-
(a) is correct (b) is incorrect


