4.3: Unions and Intersections

We can form a new set from existing sets by carrying out a set operation.

Definition: $A \cap B$

Given two sets $A$ and $B$, define their intersection to be the set

$$A \cap B = \{ x\in{\cal U} \mid x \in A \wedge x \in B \}$$

Loosely speaking, $A \cap B$ contains elements common to both $A$ and $B$.

Definition: $A \cup B$

The union of $A$ and $B$ is defined as

$$A \cup B = \{ x\in{\cal U} \mid x \in A \vee x \in B \}$$

Thus $A \cup B$ is, as the name suggests, the set combining all the elements from $A$ and $B$.

INTERSECTION

        UNION

 

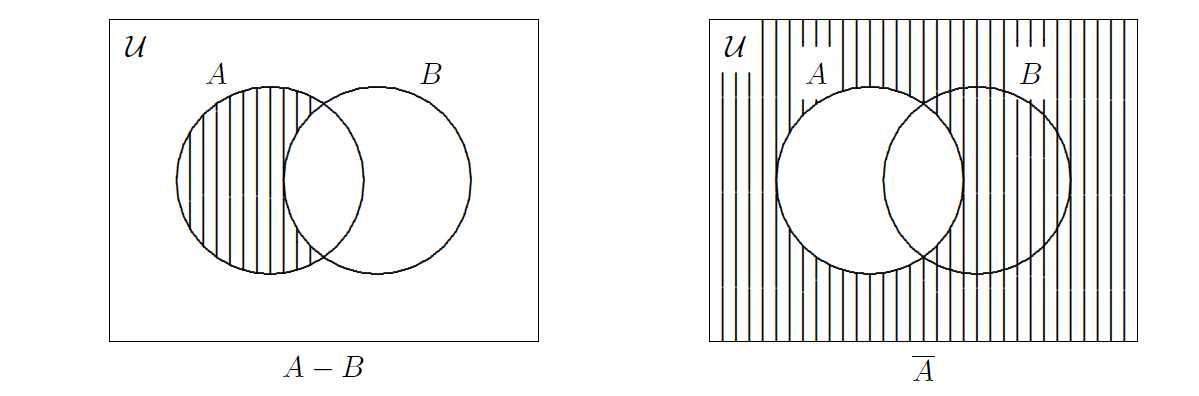
Definition: $A-B$

The set difference $A-B$, sometimes written as $A \setminus B$, is defined as

$$A- B = \{ x\in{\cal U} \mid x \in A \wedge x \not\in B \}$$

In words, $A-B$ contains elements that can only be found in $A$ but not in $B$. Operationally speaking, $A-B$ is the set obtained from $A$ by removing the elements that also belong to $B$. 

Definition: $\overline{A}$

The complement of $A$, denoted by $\overline{A}$, $A'$ or $A^c$, is defined as 

$$\overline{A} = \{ x\in{\cal U} \mid x \notin A \}$$

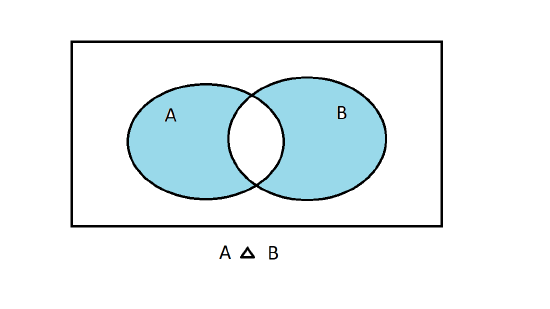
Definition: $A \bigtriangleup B$

The symmetric difference   $A \bigtriangleup B$, is defined as

$$A \bigtriangleup B = (A - B) \cup (B - A)$$  

Definition: Disjoint

Two sets are disjoint if their intersection is empty.

For example, consider $S=\{1,3,5\}$ and $T=\{2,8,10,14\}$.

$S \cap T = \emptyset$ so $S$ and $T$ are disjoint.

Remark

We would like to remind the readers that it is not uncommon among authors to adopt different notations for the same mathematical concept. Likewise, the same notation could mean something different in another textbook or even another branch of mathematics. It is important to develop the habit of examining the context and making sure that you understand the meaning of the notations when you start reading a mathematical exposition.

Example $\PageIndex{1}\label{eg:unionint-01}$

Let ${\cal U}=\{1,2,3,4,5\}$, $A=\{1,2,3\}$, and $B=\{3,4\}$. Find $A\cap B$, $A\cup B$, $A-B$, $B-A$, $A\bigtriangleup B$, $\overline{A}$, and $\overline{B}$.

Solution

We have $$\begin{aligned} A\cap B &=& \{3\}, \\ A\cup B &=& \{1,2,3,4\}, \\ A - B &=& \{1,2\}, \\ B \bigtriangleup A &=& \{1,2,4\}. \end{aligned}$$ We also find $\overline{A} = \{4,5\}$, and $\overline{B} = \{1,2,5\}$.

hands-on exercise $\PageIndex{1}\label{he:unionint-01}$

Let ${\cal U} = \{\mbox{John}, \mbox{Mary}, \mbox{Dave}, \mbox{Lucy}, \mbox{Peter}, \mbox{Larry}\}$, $$A = \{\mbox{John}, \mbox{Mary}, \mbox{Dave}\}, \qquad\mbox{and}\qquad B = \{\mbox{John}, \mbox{Larry}, \mbox{Lucy}\}.$$ Find $A\cap B$, $A\cup B$, $A-B$, $B-A$, $\overline{A}$, and $\overline{B}$.

hands-on exercise $\PageIndex{2}\label{he:unionint-02}$

If $A\subseteq B$, what would be $A-B$?

Example $\PageIndex{2}\label{eg:unionint-02}$

The set of integers can be written as the $$\mathbb{Z} = \{-1,-2,-3,\ldots\} \cup \{0\} \cup \{1,2,3,\ldots\}.$$ Can we replace $\{0\}$ with 0? Explain.

hands-on exercise $\PageIndex{3}\label{he:unionint-03}$

Explain why the following expressions are syntactically incorrect.

• $\mathbb{Z} = \{-1,-2,-3,\ldots\} \cup \;0\; \cup \{1,2,3,\ldots\}$.
• $\mathbb{Z} = \ldots,-3,-2,-1 \;\cup\; 0 \;\cup\; 1,2,3,\ldots\,$
• $\mathbb{Z} = \ldots,-3,-2,-1 \;+\; 0 \;+\; 1,2,3,\ldots\,$
• $\mathbb{Z} = \mathbb{Z} ^- \;\cup\; 0 \;\cup\; \mathbb{Z} ^+$

How would you fix the errors in these expressions?

Example $\PageIndex{3}\label{eg:unionint-03}$

For any set $A$, what are $A\cap\emptyset$, $A\cup\emptyset$, $A-\emptyset$, $\emptyset-A$ and $\overline{\overline{A}}$?

Answer

It is clear that $$A\cap\emptyset = \emptyset, \qquad A\cup\emptyset = A, \qquad\mbox{and}\qquad A-\emptyset = A.$$ From the definition of set difference, we find $\emptyset-A = \emptyset$. Finally, $\overline{\overline{A}} = A$.

Example $\PageIndex{4}\label{eg:unionint-04}$

Write, in interval notation, $[5,8)\cup(6,9]$ and $[5,8)\cap(6,9]$.

Answer

The answers are $$[5,8)\cup(6,9] = [5,9], \qquad\mbox{and}\qquad [5,8)\cap(6,9] = (6,8).$$ They are obtained by comparing the location of the two intervals on the real number line.

hands-on exercise $\PageIndex{4}\label{he:unionint-04}$

Write, in interval notation, $(0,3)\cup[-1,2)$ and $(0,3)\cap[-1,2)$.

Example $\PageIndex{5}\label{eg:unionint-05}$

We are now able to describe the following set $$\{x\in\mathbb{R} \mid (x<5) \vee (x>7)\}$$ in the interval notation. It can be written as either $(-\infty,5)\cup(7,\infty)$ or, using complement, $\mathbb{R}-[5,7\,]$. Consequently, saying $x\notin[5,7\,]$ is the same as saying $x\in(-\infty,5) \cup(7,\infty)$, or equivalently, $x\in \mathbb{R}-[5,7\,]$.

To Prove a Set is Empty

To prove a set is empty, use a proof by contradiction with these steps:

(1) Assume not.  That, is assume $\ldots$ is not empty.

(2) This means there is an element is $\ldots$ by definition of the empty set. 

(3) Let $x \in \ldots$.

(4) Come to a contradition and wrap up the proof.

 

Example $\PageIndex{6}$

Prove: $\forall A \in {\cal U}, A \cap \emptyset = \emptyset.$

Proof: Assume not. That is, assume for some set $A,$  $A \cap \emptyset \neq \emptyset.$
By definition of the empty set, this means there is an element in $A \cap \emptyset .$

Let $x \in A \cap \emptyset .$

$x \in A \wedge x\in \emptyset$ by definition of intersection.

This says $x \in \emptyset$, but the empty set has no elements!  This is a contradiction!

Thus, our assumption is false, and the original statement is true.
$\forall A \in {\cal U}, A \cap \emptyset = \emptyset.$

 

Set Properties

Notes:

(a) These properties should make sense to you and you should be able to prove them.  However, you are not to use them as reasons in a proof.  Rather your justifications for steps in a proof need to come directly from definitions. The exception to this is DeMorgan's Laws which you may reference as a reason in a proof.

(b) You do not need to memorize these properties or their names.  However, you should know the meanings of: commutative, associative and distributive.  Also, you should know DeMorgan's Laws by name and substance.

The following properties hold for any sets $A$, $B$, and $C$ in a universal set ${\cal U}$.

1. Commutative properties: $\begin{array}[t]{l} A \cup B = B \cup A, \\ A \cap B = B \cap A. \end{array}$
2. Associative properties: $\begin{array}[t]{l} (A \cup B) \cup C = A \cup (B \cup C), \\ (A \cap B) \cap C = A \cap (B \cap C). \end{array}$
3. Distributive laws: $\begin{array}[t]{l} A \cup (B \cap C) = (A \cup B) \cap (A \cup C), \\ A \cap (B \cup C) = (A \cap B) \cup (A \cap C). \end{array}$
4. Idempotent laws: $\begin{array}[t]{l} A \cup A = A, \\ A \cap A = A. \end{array}$
5. De Morgan’s laws: $\begin{array}[t]{l} \mbox{  (a)  } \overline{A \cup B} = \overline{A} \cap \overline{B}, \\ \mbox{  (b)  }  \overline{A \cap B} = \overline{A} \cup \overline{B}. \end{array}$
6. Laws of the excluded middle, or inverse laws: $\begin{array}[t]{l} A \cup \overline{A} = {\cal U}, \\ A \cap \overline{A} = \emptyset. \end{array}$

As an illustration, we shall prove the distributive law $$A \cup (B \cap C) = (A \cup B) \cap (A \cup C).$$  

We need to show that $$A \cup (B \cap C) \subseteq (A \cup B) \cap (A \cup C), \qquad\mbox{and}\qquad (A \cup B) \cap (A \cup C) \subseteq A \cup (B \cap C).$$

Here is a proof of the distributive law $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$.

Proof
 

First we will show $A \cup (B \cap C) \subseteq (A \cup B) \cap (A \cup C).$
Let $x\in A\cup(B\cap C)$.
$x\in A\vee x \in B\cap C$ by definition of union.

Case 1: $x \in A.$
Since $x \in A$,  $x \in A \cup B,$ by definition of union and $x \in A \cup C,$ by definition of union.
$\therefore x \in (A \cup B) \cap (A \cup C)$, by definition of intersection.

Case 2: $x \in B\cap C.$
$x \in B\wedge x\in C,$by definition of intersection.
$x \in A \cup B,$ by definition of union and $x \in A \cup C,$ by definition of union.
$\therefore x \in (A \cup B) \cap (A \cup C)$, by definition of intersection.

We have shown if $x\in A\cup(B\cap C)$ then $x \in (A \cup B) \cap (A \cup C)$.
So, by definition of subset, $A \cup (B \cap C) \subseteq (A \cup B) \cap (A \cup C).$

Next, we will show $(A \cup B) \cap (A \cup C)\subseteq A \cup (B \cap C).$
Let $x \in (A \cup B) \cap (A \cup C).$
$x\in (A\cup B) \wedge x \in (A\cup C)$ by definition of intersection.
Case 1: $x \in A.$
Since $x \in A,$ we have $x\in A\cup(B\cap C)$ by definition of union.

Case 2: $x \notin A.$
Since $x\in (A\cup B),$ $x \in A \vee x \in B$ by definition of union, so $x$ must be an element of $B.$
Furthermore, since $x\in (A\cup C),$ $x \in A \vee x \in C$ by definition of union, so $x$ must be an element of $C.$
We have $x \in B \wedge x \in C,$ thus  $x\in B\cap C$. by definition of intersection.
And so,  $x\in A\cup(B\cap C)$. by definition of union.

In both cases, if $x \in (A \cup B) \cap (A \cup C),$ then $x\in A\cup(B\cap C.)$
So, by definition of subset, $(A \cup B) \cap (A \cup C) \subseteq A \cup (B \cap C.)$

It follows that $A \cup (B \cap C) = (A\cup B) \cap (A\cup C)$, by definition of equality of sets.

hands-on exercise $\PageIndex{5}\label{he:unionint-05}$

Prove that $A\cap(B\cup C) = (A\cap B)\cup(A\cap C)$.

hands-on exercise $\PageIndex{6}\label{he:unionint-06}$

Prove that if $A\subseteq B$ and $A\subseteq C$, then $A\subseteq B\cap C$.

Discussion

Let us start with a draft. The statement we want to prove takes the form of $$(A\subseteq B) \wedge (A\subseteq C) \Rightarrow A\subseteq B\cap C.$$ Hence, what do we assume and what do we want to prove?

Assume:

Want to Prove:

Did you put down we assume $A\subseteq B$ and $A\subseteq C$, and we want to prove $A\subseteq B\cap C$? Great! Now, what does it mean by $A\subseteq B$? How about $A\subseteq C$? What is the meaning of $A\subseteq B\cap C$?

$A\subseteq B$ means: For any $x\in{\cal U}$, if $x\in A$, then $x\in B$ as well.

$A\subseteq C$ means:

$A\subseteq B\cap C$ means:

How can you use the first two pieces of information to obtain what we need to establish?

Now it is time to put everything together, and polish it into a final version. Remember three things:

• the outline of the proof,
• the reason in each step of the main argument, and
• the introduction and the conclusion.

Put the complete proof in the space below.

Here are two results involving complements.

Theorem $\PageIndex{1}\label{thm:subsetsbar}$

For any two sets $A$ and $B$, we have $A \subseteq B \Leftrightarrow \overline{B} \subseteq \overline{A}$.

Theorem $\PageIndex{2}\label{thm:genDeMor}$

For any sets $A$, $B$ and $C$,  

(a) $A-(B \cup C)=(A-B) \cap (A-C)$

(b) $A-(B \cap C)=(A-B) \cup (A-C)$

Summary and Review

• Memorize the definitions of intersection, union, and set difference. We rely on them to prove or derive new results.
• The intersection of two sets $A$ and $B$, denoted $A\cap B$, is the set of elements common to both $A$ and $B$. In symbols, $\forall x\in{\cal U}\,\big[x\in A\cap B \Leftrightarrow (x\in A \wedge x\in B)\big]$.
• The union of two sets $A$ and $B$, denoted $A\cup B$, is the set that combines all the elements in $A$ and $B$. In symbols, $\forall x\in{\cal U}\,\big[x\in A\cup B \Leftrightarrow (x\in A\vee x\in B)\big]$.
• The set difference between two sets $A$ and $B$, denoted by $A-B$, is the set of elements that can only be found in $A$ but not in $B$. In symbols, it means $\forall x\in{\cal U}\, \big[x\in A-B \Leftrightarrow (x\in A \wedge x\notin B)\big]$.
• The symmetric difference between two sets $A$ and $B$, denoted by $A \bigtriangleup B$, is the set of elements that can be found in $A$ and in $B$, but not in both $A$ and $B$.  In symbols, it means $\forall x\in{\cal U}\, \big[x\in A \bigtriangleup B \Leftrightarrow x\in A-B  \vee x\in B-A)\big]$.

Exercises 

Exercise $\PageIndex{1}\label{ex:unionint-01}$

Write each of the following sets by listing its elements explicitly.

(a) $[-4,4]\cap\mathbb{Z}$

(b) $(-4,4]\cap\mathbb{Z}$

(c) $(-4,\infty)\cap\mathbb{Z}$

(d) $(-\infty,4]\cap\mathbb{N}$

(e) $(-4,\infty)\cap\mathbb{Z}^-$

(f) $(4,5)\cap\mathbb{Z}$
 

Answer

(a) $\{-4,-3,-2,-1,0,1,2,3,4\}$

(b) $\{-3,-2,-1,0,1,2,3,4\}$

(c) $\{-3,-2,-1,0,1,2,3,\ldots\}$

Exercise $\PageIndex{2}\label{ex:unionint-02}$

Assume ${\cal U} = \mathbb{Z}$, and let

$A=\{\ldots, -6,-4,-2,0,2,4,6, \ldots \} = 2\mathbb{Z},$

$B=\{\ldots, -9,-6,-3,0,3,6,9, \ldots \} = 3\mathbb{Z},$

$C=\{\ldots, -12,-8,-4,0,4,8,12, \ldots \} = 4\mathbb{Z}.$

 Describe the following sets by listing their elements explicitly.

(a) $A\cap B$

(b) $C-A$

(c) $A-B$

(d) $A\cap\overline{B}$

(e) $B-A$

(f) $B\cup C$

(g) $(A\cup B)\cap C$

(h) $(A\cup B)-C$

Exercise $\PageIndex{3}\label{ex:unionint-03}$

Are these statements true or false?

(a) $[1,2]\cap[2,3] = \emptyset$

(b) $[1,2)\cup(2,3] = [2,3]$

Answer

(a) false (b) false

Exercise $\PageIndex{4}\label{ex:unionint-04}$

Let the universal set ${\cal U}$ be the set of people who voted in the 2012 U.S. presidential election. Define the subsets $D$, $B$, and $W$ of ${\cal U}$ as follows: $$\begin{aligned} D &=& \{x\in{\cal U} \mid x \mbox{ registered as a Democrat}\}, \\ B &=& \{x\in{\cal U} \mid x \mbox{ voted for Barack Obama}\}, \\ W &=& \{x\in{\cal U} \mid x \mbox{ belonged to a union}\}. \end{aligned}$$ Express the following subsets of ${\cal U}$ in terms of $D$, $B$, and $W$.

(a) People who did not vote for Barack Obama.

(b) Union members who voted for Barack Obama.

(c) Registered Democrats who voted for Barack Obama but did not belong to a union.

(d) Union members who either were not registered as Democrats or voted for Barack Obama.

(e) People who voted for Barack Obama but were not registered as Democrats and were not union members.

(f) People who were either registered as Democrats and were union members, or did not vote for Barack Obama.

Exercise $\PageIndex{5}\label{ex:unionint-05}$

An insurance company classifies its set ${\cal U}$ of policy holders by the following sets: $$\begin{aligned} A &=& \{x\mid x\mbox{ drives a subcompact car}\}, \\ B &=& \{x\mid x\mbox{ drives a car older than 5 years}\}, \\ C &=& \{x\mid x\mbox{ is married}\}, \\ D &=& \{x\mid x\mbox{ is over 21 years old}\}, \\ E &=& \{x\mid x\mbox{ is a male}\}. \end{aligned}$$ Describe each of the following subsets of ${\cal U}$ in terms of $A$, $B$, $C$, $D$, and $E$.

(a) Male policy holders over 21 years old.

(b) Policy holders who are either female or drive cars more than 5 years old.

(c) Female policy holders over 21 years old who drive subcompact cars.

(d) Male policy holders who are either married or over 21 years old and do not drive subcompact cars.

Answer

(a) $E\cap D$ (b) $\overline{E}\cup B$

Exercise $\PageIndex{6}\label{ex:unionint-06}$

Let $A$ and $B$ be arbitrary sets. Complete the following statements.

(a) $A\subseteq B \Leftrightarrow A\cap B =$        ___________________

(b) $A\subseteq B \Leftrightarrow A\cup B =$        ___________________

(c) $A\subseteq B \Leftrightarrow A - B =$           ___________________

(d) $A\subset B \Leftrightarrow (A-B=$  ___________________$\wedge\,B-A\neq$ ___________________ $)$

(e) $A\subset B \Leftrightarrow (A\cap B=$  ___________________$\wedge\,A\cap B\neq$ ___________________  $)$

(f) $A - B = B - A \Leftrightarrow$           ___________________

Exercise $\PageIndex{7}\label{ex:unionint-07}$

Give examples of sets $A$ and $B$ such that $A\in B$ and $A\subset B$.

Answer

For example, take $A=\{x\}$, and $B=\{\{x\},x\}$.

Exercise $\PageIndex{8}\label{ex:unionint-08}$

(a) Prove De Morgan’s law, (a) .

(b) Prove De Morgan’s law, (b) .

Exercise $\PageIndex{9}\label{ex:unionint-09}$

Let $A$, $B$, and $C$ be any three sets. Prove that if $A\subseteq C$ and $B\subseteq C$, then $A\cup B\subseteq C$.

Answer

Assume $A\subseteq C$ and $B\subseteq C$, we want to show that $A\cup B \subseteq C$.

Let $x\in A\cup B$. we want to show that $x\in C$ as well.

Since $x\in A\cup B$, then either $x\in A$ or $x\in B$ by definition of union.

Case 1: If $x\in A$, then $A\subseteq C$ implies that $x\in C$ by definition of subset.

Case 2: If $x\in B$, then $B\subseteq C$ implies that $x\in C$ by definition of subset.

 

In both cases, we find $x\in C$. So, if $x\in A\cup B$ then $x\in C$.

This proves that $A\cup B\subseteq C$ by definition of subset.

$\therefore$ For any sets $A$, $B$, and $C$ if $A\subseteq C$ and $B\subseteq C$, then $A\cup B\subseteq C$.

Exercise $\PageIndex{10}\label{ex:unionint-10}$

Prove Theorem 4.3.1

Exercise $\PageIndex{11}\label{ex:unionint-11}$

(a) Prove Theorem 4.3.2 part (a)

(b) Prove Theorem 4.3.2 part (b)

Exercise $\PageIndex{12}\label{ex:unionint-12}$

Let $A$, $B$, and $C$ be any three sets. Prove that

(a) $A-B=A\cap\overline{B}$

(b) $A=(A-B)\cup(A\cap B)$

(c) $A-(B-C) = A\cap(\overline{B}\cup C)$

(d) $(A-B)-C = A-(B\cup C)$

Exercise $\PageIndex{13}\label{ex:unionint-13}$

Comment on the following statements. Are they syntactically correct?

(a) $x\in A \cap x\in B \equiv x\in A\cap B$

(b) $x\in A\wedge B \Rightarrow x\in A\cap B$

Answer

(a) The notation $\cap$ is used to connect two sets, but “$x\in A$” and “$x\in B$” are both logical statements. We should also use $\Leftrightarrow$ instead of $\equiv$. The statement should have been written as “$x\in A \,\wedge\, x\in B \Leftrightarrow x\in A\cap B$.”

(b) If we read it aloud, it sounds perfect: $$\mbox{If $x$ belongs to $A$ and $B$, then $x$ belongs to $A\cap B$}.$$ The trouble is, every notation has its own meaning and specific usage. In this case, $\wedge$ is not exactly a replacement for the English word “and.” Instead, it is the notation for joining two logical statements to form a conjunction. Before $\wedge$, we have “$x\in A$,” which is a logical statement. But, after $\wedge$, we have “$B$,” which is a set, and not a logical statement. It should be written as “$x\in A\,\wedge\,x\in B \Rightarrow x\in A\cap B$.”

Exercise $\PageIndex{14}\label{ex:unionint-14}$

Prove or disprove each of the following statements about arbitrary sets $A$ and $B$. If you think a statement is true, prove it; if you think it is false, provide a counterexample.

(a) $\mathscr{P}(A\cap B) = \mathscr{P}(A)\cap\mathscr{P}(B)$

(b) $\mathscr{P}(A\cup B) = \mathscr{P}(A)\cup\mathscr{P}(B)$

(c) $\mathscr{P}(A - B) = \mathscr{P}(A) - \mathscr{P}(B)$

Remark

To show that two sets $U$ and $V$ are equal, we usually want to prove that $U \subseteq V$ and $V \subseteq U$.  For the subset relationship, we start with let $x\in U$. In this problem, the element $x$ is actually a set. Since we usually use uppercase letters to denote sets, for (a) we should start the proof of the subset relationship  “Let $S\in\mathscr{P}(A\cap B)$,”  using an uppercase letter to emphasize the elements of $\mathscr{P}(A\cap B)$ are sets. These remarks also apply to (b) and (c).

Exercise $\PageIndex{15}$

Let ${\cal U}=\{1,2,3,4,5,6,7,8\}$, $A=\{2,4,6,8\}$, $B=\{3,5\}$, $C=\{1,2,3,4\}$ and$D=\{6,8\}$. Find

(a) $A\cap C$                   (b) $A\cap B$                    (c) $\emptyset \cup B$   

(d) $\emptyset \cap B$                  (e) $A-(B \cup C)$              (f) $C-B$                   

(g) $A\bigtriangleup C$                (h) $A \cup {\cal U}$                  (i)  $A\cap D$                       

(j) $A\cup D$                  (k) $B\cap D$                      (l) $B\bigtriangleup C$   

(m)  $A \cap {\cal U}$                 (n) $\overline{A}$                      (o) $\overline{B}$.                 

(p) $D \cup (B \cap C)$        (q) $\overline{A \cup C}$            (r) $\overline{A} \cup \overline{C}$

(s) Which pairs of sets are disjoint?

Answer    

(a) $\{2,4\}$            (b) $\emptyset$       (c) $B$               (d)  $\emptyset$    

Exercise $\PageIndex{16}$

Prove:

If $A \subseteq B$ then $A-B= \emptyset.$