5.5: Indexed Families of Sets
- Last updated
- Sep 29, 2021
- Save as PDF
- Page ID
- 86126
( \newcommand{\kernel}{\mathrm{null}\,}\)
Preview Activity 5.5.1: The Union and Intersection of a Family of Sets
In Section 5.3, we discussed various properties of set operations. We will now focus on the associative properties for set union and set intersection. Notice that the definition of “set union” tells us how to form the union of two sets. It is the associative law that allows us to discuss the union of three sets. Using the associate law, if A, B, and C are subsets of some universal set, then we can define A∪B∪C to be (A∪B)∪C or A∪(B∪C). That is,
A∪B∪C=(A∪B)∪C=A∪(B∪C).
For this activity, the universal set is N and we will use the following four sets:
A= {1, 2, 3, 4, 5}
B= {2, 3, 4, 5, 6}
C= {3, 4, 5, 6, 7}
D= {4, 5, 6, 7, 8}
- Use the roster method to specify the sets A∪B∪C, B∪C∪D, A∩B∩C, and B∩C∩D.
- Use the roster method to specify each of the following sets. In each case, be sure to follow the order specified by the parentheses.
(a) (A∪B∪C)∪D
(b) A∪(B∪C∪D)
(c) A∪(B∪C)∪D
(d) (A∪B)∪(C∪D)
(e) (A∩B∩C)∩D
(f) A∩(B∩C∩D)
(g) A∩(B∩C)∩D
(h) (A∩B)∩(C∩D) - Based on the work in Part (2), does the placement of the parentheses matter when determining the union (or intersection) of these four sets? Does this make it possible to define A∪B∪C∪D and A∩B∩C∩D?
We have already seen that the elements of a set may themselves be sets. For example, the power set of a set T, P(T), is the set of all subsets of T. The phrase, “a set of sets” sounds confusing, and so we often use the terms collection and family when we wish to emphasize that the elements of a given set are themselves sets. We would then say that the power set of T is the family (or collection) of sets that are subsets of T.
One of the purposes of the work we have done so far in this preview activity was to show that it is possible to define the union and intersection of a family of sets.
Definition
Let C be a family of sets. The union over C is defined as the set of all elements that are in at least one of the sets in C. We write
⋃X∈CX={x∈U | x∈X for some X∈C}
The intersection over C is defined as the set of all elements that are in all of the sets in C. That is,
⋂X∈CX={x∈U | x∈X for some X∈C}
For example, consider the four sets A, B, C, and D used earlier in this preview activity and the sets
S= {5, 6, 7, 8, 9} and T= {6, 7, 8, 9, 10}
We can then consider the following families of sets: A={A,B,C,D} and B={A,B,C,D,S,T}
- Explain why
⋃X∈AX=A∪B∪C∪D and ⋂X∈AX=A∩B∩C∩D
and use your work in (1), (2), and (3) to determine ⋃X∈AX and ⋂X∈AX.
- Use the roster method to specify ⋃X∈BX and ⋂X∈BX
6. Use the roster method to specify the sets (⋃X∈AX)c and ⋂X∈AXc. Remember that the universal set is N.
Preview Activity 5.5.2: An Indexed Family of Sets
We often use subscripts to identify sets. For example, in Preview Activity 5.5.1, instead of using A, B, C, and D as the names of the sets, we could have used A1, A2, A3, and A4. When we do this, we are using the subscript as an identifying tag, or index, for each set. We can also use this idea to specify an infinite family of sets. For example, for each natural number n, we define
Cn={n,n+1,n+2,n+3,n+4}.
So if we have a family of sets C={C1,C2,C3,C4}, we use the notation ⋃4j=1Cj to mean the same thing as ⋃x∈CX.
- Determine ⋃4j=1Cj and ⋂4j=1Cj
We can see that with the use of subscripts, we do not even have to define the family of sets A. We can work with the infinite family of sets
C∗={An | n∈N}
and use the subscripts to indicate which sets to use in a union or an intersection. - Use the roster method to specify each of the following pairs of sets. The universal set is N.
(a) ⋃6j=1Cj and ⋂6j=1Cj
(b) ⋃8j=1Cj and ⋂8j=1Cj
(c) ⋃8j=4Cj and ⋂8j=4Cj
(d) (⋂4j=1Cj)c and ⋃4j=1Ccj
The Union and Intersection over an Indexed Family of Sets
One of the purposes of the preview activities was to show that we often encounter situations in which more than two sets are involved, and it is possible to define the union and intersection of more than two sets. In Preview Activity 5.5.2, we also saw that it is often convenient to “index” the sets in a family of sets. In particular, if n is a natural number and A={A1,A2,...,An} is a family of n sets, then the union of these n sets, denoted by A1∪A2∪⋅⋅⋅∪An or ⋃nj=1Aj, is defined as
n⋃j=1Aj={x∈U | x∈Aj, for some j with 1≤j≤n}.
We can also defined the intersection of these n sets, denoted by A1∩A2∩⋅⋅⋅∩An or ⋂nj=1Aj, as
n⋂j=1Aj={x∈U | x∈Aj, for some j with 1≤j≤n}.
We can also extend this idea to define the union and intersection of a family that consists of infinitely many sets. So if B={B1,B2,...,Bn,...}, then
⋃∞j=1Bj={x∈U | x∈Bj, for some j with j≥1}, and
⋂∞j=1Bj={x∈U | x∈Bj, for all j with j≥1}.
Progress Check 5.26 (An Infinite Family of Sets)
For each natural number n, let An={1,n,n2}. For example,
A1={1}, A2={1,2,4}, A3={1,3,9},
and
⋃3j=1Aj={1,2,3,4,9}, ⋂3j=1Aj={1}.
Determine each of the following sets:
- ⋃6j=1Aj
- ⋂6j=1Aj
- ⋃6j=3Aj
- ⋂6j=3Aj
- ⋃∞j=1Aj
- ⋂∞j=1Aj
- Answer
-
Add texts here. Do not delete this text first.
In all of the examples we have studied so far, we have used N or a subset of N to index or label the sets in a family of sets. We can use other sets to index or label sets in a family of sets. For example, for each real number x, we can define Bx to be the closed interval [x, x + 2]. That is,
Bx={y∈R | x≤y≤x+2}.
So we make the following definition. In this definition,∧ is the uppercase Greek letter lambda and α is the lowercase Greek letter alpha.
Definition
Let Λ be a nonempty set and suppose that for each α∈∧, there is a corresponding set Aα. The family of sets {Aα | α∈∧} is called an indexed family of sets indexed by ∧. Each α∈∧ is called an index and Λ is called an indexing set.
Progress Check 5.27 (Indexed Families of Sets)
In each of the indexed families of sets that we seen so far, if the indices were different, then the sets were different. That is, if Λ is an indexing for the family of sets A={Aα | α∈∧}, then if α,β∈∧ and α≠β, then Aα≠Aβ. (Note: The letter β is the Greek lowercase beta.)
- Let Λ={1,2,3,4}, and for each n∈Λ, let An={2n+6,16−3n}, and let A={A1,A2,A3,A4}. Determine A1, A2, A3, and A4.
- Is the following statement true or false for the indexed family A in (1)?
- Now let Λ=R. For each x∈R, define Bx={0,x2,x4}. Is the following statement true for the indexed family of set B={Bx | x∈R}?
For all x,y∈R, if x≠y, then Bx≠By.
- Answer
-
Add texts here. Do not delete this text first.
We now restate the definitions of the union and intersection of a family of sets for an indexed family of sets.
Definition
Let Λ be a nonempty indexing set and let A={Aα | α∈Λ} be an indexed family of sets. The union over A is defined as the set of all elements that are in at least one of sets Aα, where α∈∧. We write
⋃α∈ΛAα={x∈U | there exits an α∈Λ with x∈Aα}.
The intersection over (\mathcal{A}\) is the set of all elements that are in all of the sets Aα for each α∈Λ. That is,
⋂α∈∧Aα={x∈U | for all α∈∧,x∈Aα}.
Example 5.28 (A Family of Sets Indexed by the Positive Real Numbers)
For each positive real numbe α, let Aα be the interval (-1, α]. That is,
Aα={x∈R | −1<x≤α}.
If we let R+ be the set of positive real numbers, then we have a family of sets indexed by R+. We will first determine the union of this family of sets. Notice that for each α∈mathbbR+, α∈Aα, and if y is a real number with −1<y≤0, then y∈Aα. Also notice that if y∈R and y<−1, then for each α∈mathbbR+, y∉Aα. With these observations, we conclude that
⋃α∈R+Aα=(−1,∞)={x∈R | −1<x}.
To determine the intersection of this family, notice that
- if y∈R and y<−1, then for each α∈R+, y∉Aα;
- if y∈R and −1<y≤0, then y∈Aα for each α∈mathbbR+; and
- if y∈R and y>0, then of we let β=y2, y>β and y∉Aβ.
From these observations, we conclude that
⋂α∈R+Aα=(−1,0]={x∈R | −1<x≤0}.
Progress Check 5.29 (A Continuation of Example 5.28)
Using the family of sets from Example 5.28, for each α∈mathbbR+, we see that
Acα=(−∞,1]∪(α,∞).
Use the results from Example 5.28 to help determine each of the following sets. For each set, use either interval notation or set builder notation.
- (⋃α∈R+Aα)c
- (⋂α∈R+Aα)c
- ⋂α∈R+Acα
- ⋃α∈R+Acα
- Answer
-
Add texts here. Do not delete this text first.
Properties of Union and Intersection
In Theorem 5.30, we will prove some properties of set operations for indexed families of sets. Some of these properties are direct extensions of corresponding properties for two sets. For example, we have already proved De Morgan’s Laws for two sets in Theorem 5.20. The work in the preview activities and Progress Check 5.29 suggests that we should get similar results using set operations with an indexed family of sets. For example, in Preview Activity 5.5.2, we saw that
(⋂4j=1Aj)c=⋃4j=1Acj.
Theorem 5.30.
Let Λ be a nonempty indexing set and let A={Aα | α∈∧} be an indexed family of sets. Then
- For each β∈Λ, ⋂α∈ΛAα⊆Aβ
- For each β∈Λ, Aβ⊆⋃α∈ΛAα
- (⋂α∈ΛAα)c=⋃α∈ΛAcα
- (⋃α∈ΛAα)c=⋂α∈ΛAcα
Parts (3) and (4) are known as De Morgan's Laws.
- Proof
-
We will prove Parts (1) and (3). The proofs of Parts (2) and (4) are included in Exercise (4). So we let Λ be a nonempty indexing set and let mathcalA={Aα | α∈Λ} be an indexed family of sets. To prove Part (1), we let β∈Λ and note that if x∈⋂α∈ΛAα, then x∈Aα, for all α∈Λ. Since β is one element in Λ, we may conclude that x∈Aβ. This proves that ⋂α∈ΛAα⊆Aβ.
To prove Part (3), we will prove that each set is a subset of the other set. We first let x∈(⋂α∈ΛAα)c. This means that x∉(⋂α∈ΛAα), and this means that
there exists a β∈Λ such that x∉Aβ.
Hence, x∈Acβ, which implies that x∈⋃α∈ΛAcα. Therefore, we have proved that
(⋂α∈ΛAα)c⊆⋃α∈ΛAcα.
We now let y∈⋃α∈ΛAcα. This means that there exists a β∈Λ such that y∈Acβ or y∉Aβ. However, since y∉Aβ, we may conclude that y∉⋂α∈ΛAα and, hence, y∈(⋂α∈ΛAα)c. This proves that
⋃α∈ΛAcα⊆(⋂α∈ΛAα)c.
Using the results in (5.5.4) and (5.5.5), we have proved that (⋂α∈ΛAα)c=⋃α∈ΛAcα.
Many of the other properties of set operations are also true for indexed families of sets. Theorem 5.31 states the distributive laws for set operations.
Theorem 5.31.
Let Λ be a nonempty indexing set and let A={Aα | α∈Λ} be an indexed family of sets, and let B be a set. Then
- B∩(⋃α∈ΛAα)=⋃α∈Λ(B∩Aα), and
- B∪(⋂α∈ΛAα)=⋂α∈Λ(B∪Aα).
- Proof
-
The proof of Theorem 5.31 is Exercise (5).
Pairwise Disjoint Families of Sets
In Section 5.2, we defined two sets A and B to be disjoint provided that A∩B=∅. In a similar manner, if Λ is a nonempty indexing set and A={Aα | α∈Λ} is an indexed family of sets, we can say that this indexed family of sets is disjoint provided that ⋂α∈ΛAα=∅. However, we can use the concept of two disjoint sets to define a somewhat more interesting type of “disjointness” for an indexed family of sets.
Definition
Let Λ be a nonempty indexing set, and let A={Aα | α∈Λ} be an indexed family of sets. We say that A is pair wise disjoint provided that for all α and β in Λ, if Aα≠Aβ, then Aα∩Aβ=∅.
Progress Check 5.32 (Disjoint Families of Sets)
Figure 5.7 shows two families of sets,
A= {A1, A2, A3, A4} and B= {B1, B2, B3, B4}.
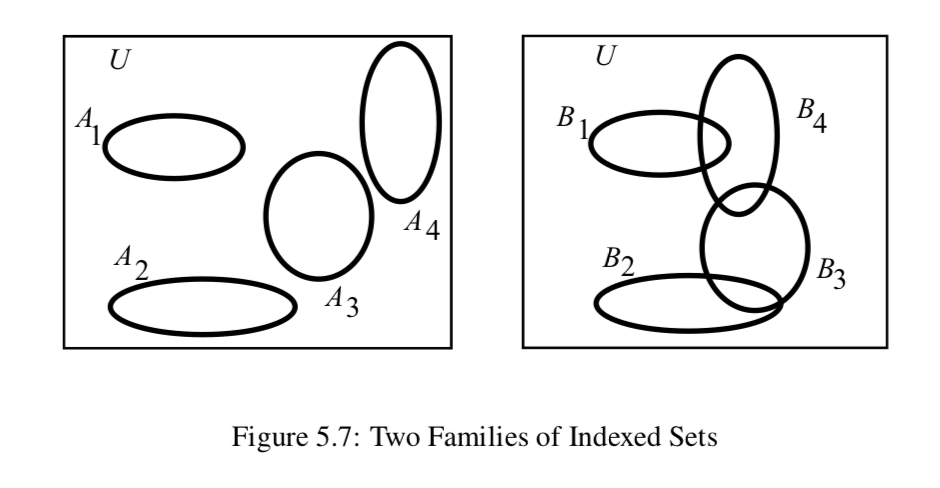
- Is the family of sets A a disjoint family of sets? A pairwise disjoint family of sets?
- Is the family of sets B a disjoint family of sets? A pairwise disjoint family of sets?
Now let the universal be R. For each n∈N, let Cn= (n,∞), and let C={Cn | n∈N}. - Is the family of sets C a disjoint family of sets? A pairwise disjoint family of sets?
- Answer
-
Add texts here. Do not delete this text first.
Exercise 5.5.1
- For each natural number n, let An={n,n+1,n+2,n+3}. Use the roster method to specify each of the following sets:
(a) ⋂3j=1Aj
(b) ⋃3j=1Aj
(c) ⋂7j=3Aj
(d) ⋃7j=3Aj
(e) A9∩(⋃7j=3Aj)
(f) ⋃7j=3(A9∩Aj) - For each natural number n, let An={k∈N | k≥n}. Use the roster method or set builder notation to specify each of the following sets:
(a) ⋂5j=1Aj
(b) (⋂5j=1Aj)c
(c) ⋂5j=1Acj
(d) ⋃5j=1Acj
(e) ⋃5j=1Aj
(f) (⋃5j=1Aj)c
(g) \(\bigcap_{j \in \mathbb{N}^{} A_j\)
(h) \(\bigcup_{j \in \mathbb{N}^{} A_j\) - For each positive real number r, define Tr to be the closed interval [−r2,r2]. That is
Tr={x∈R | −r2≤x≤r2}.
Let ∧={m∈N | 1≤m≤10}. Use either interval notation or set builder notation to specify each of the following sets:
(a) ⋃k∈∧Tk
(b) ⋂k∈∧Tk
(c) ⋃r∈R+Tk
(d) ⋂r∈R+Tk
(e) ⋃r∈NTk
(f) ⋂r∈NTk - Prove Parts (2) and (4) of Theorem 5.30. Let Λ be a nonempty indexing set and let A={Aα | α∈Λ} be an indexed family of sets.
(a) For each β∈Λ, Aβ⊆⋃α∈ΛAα.
(b) (⋃α∈ΛAα)c=⋂α∈ΛAcα - Prove Theorem 5.31. Let Λ be a nonempty indexing set, let A={Aα | α∈Λ} be an indexed family of sets, and let B be a set. Then
(a) B∩(⋃α∈ΛAα)=⋃α∈Λ(B∩Aα), and
(b) B∪(⋂α∈ΛAα)=⋂α∈Λ(B∪Aα). - Let Λ and Γ be nonempty indexing sets and let A={Aα | α∈Λ} and B={Bβ | β∈Γ} be indexed families of sets. Use the distributive laws in Exercise (5) to:
(a) Write \((\bigcup_{\alpha \in \Lambda}^{} A_{\alpha}) \cap (\bigcup_{\beta \in \Gamma}^{} B_{\beta}) as a union of intersections of two sets.
(b) Write \((\bigcap_{\alpha \in \Lambda}^{} A_{\alpha}) \cup (\bigcap_{\beta \in \Gamma}^{} B_{\beta}) as a union of intersections of two sets. - Let Λ be a nonempty indexing set and let A={Aα | α∈Λ} be an indexed family of sets. Also, assume that Γ⊆Λ and Γ≠∅. (Note: The letter Γ is the uppercase Greek letter gamma.) Prove that
(a) ⋃α∈ΓAα⊆⋃α∈ΛAα
(b) ⋂α∈ΛAα⊆⋂α∈ΓAα - Let Λ be a nonempty indexing set and let A={Aα | α∈Λ} be an indexed family of sets.
(a) Prove that if B is a set such that B⊆Aα for every α∈Λ, then B⊆⋂α∈ΛAα.
(b) Prove that if C is a set such that Aα⊆C for every α∈Λ, then ⋂α∈ΛAα⊆C. - For each natural number n, let An={x∈R | n−1<x<n}. Prove that {An | n∈N} is a pairwise disjoint family of sets and that ⋃n∈NAn=(R+−N).
- For each natural number n, let An={k∈N | k≥n}. Determine if the following statements are true or false. Justify each conclusion.
(a) For all j,k∈N, if j≠k, then Aj∩Ak≠∅.
(b) ⋂k∈NAk=∅. - Give an example of an indexed family of sets {An | n∈N} such all three of the following conditions are true:
(i) For each m∈N, Am⊆(0,1);
(ii) For each j,k∈N, if j≠k, then Aj∩Ak≠∅; and
(iii) ⋂k∈NAk=∅. - Let Λ be a nonempty indexing set, let A={Aα | α∈Λ} be an indexed family of sets, and let B be a set. Use the results of Theorem 5.30 and Theorem 5.31 to prove each of the following:
(a) (⋃α∈ΛAα)−B=⋃α∈Λ(Aα−B)
(b) (⋂α∈ΛAα)−B=⋂α∈Λ(Aα−B)
(c) B−(⋃α∈ΛAα)=⋂α∈ΛB−(Aα)
(d) B−(⋂α∈ΛAα)=⋃α∈ΛB−(Aα)
Explorations and Activities - An Indexed Family of Subsets of the Cartesian Plane. Let R∗ be the set of nonnegative real numbers, and for each r∈R∗, let
Cr={(x,y)∈R×R | x2+y2=r2}Dr={(x,y)∈R×R | x2+y2≤r2}Tr={(x,y)∈R×R | x2+y2>r2}=Dcr.If r>0, then the set Cr is the circle of radius r with center at the origin as shown in Figure 5.8, and the set Dr is the shaded disk (including the boundary) shown in Figure 5.8.
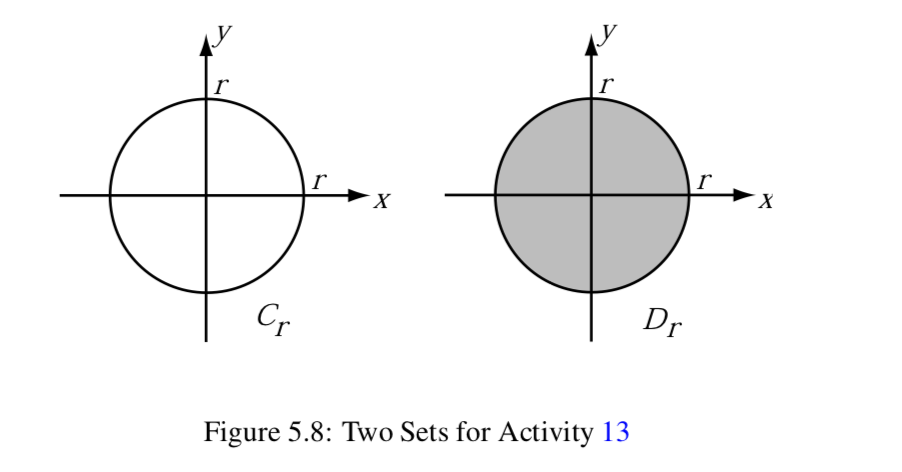
(a) Determine ⋃r∈R∗Cr and ⋂r∈R∗Cr
(b) Determine ⋃r∈R∗Dr and ⋂r∈R∗Dr
(c) Determine ⋃r∈R∗Tr and ⋂r∈R∗Tr
(d) Let C={Cr | r∈R∗}, D={Dr | r∈R∗}, and T={Tr | r∈R∗}. Are any of these indexed families of sets pairwise disjoint? Explain.
Now let I be the closed interval [0, 2] and let J be the closed interval [1, 2].
(e) Determine ⋃r∈ICr, ⋂r∈ICr, ⋃r∈JCr, and ⋂r∈JCr
(f) Determine ⋃r∈IDr, ⋂r∈IDr, ⋃r∈JDr, and ⋂r∈JDr
(g) Determine (⋃r∈IDr)c, (⋂r∈IDr)c, (⋃r∈JDr)c, and (bigcapr∈JDr)c
(h) Determine ⋃r∈ITr, ⋂r∈ITr, ⋃r∈JTr, and ⋂r∈JTr
(i) Use De Morgan's Laws to explain the relationship between your answers in Parts (13g) and (13h).
- Answer
-
Add texts here. Do not delete this text first.


