7.1: Intro, Probability and Pigeonhole Principle

Last updated
Save as PDF

Page ID: 28711

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Intro: What is Combinatorics?

Combinatorics studies the arrangements of objects according to some rules. The questions that can be asked include

Existence. Do the arrangements exist?
Classification. If the arrangements exist, how can we characterize and classify them?
Enumeration. How many arrangements are there?
Construction. Is there an algorithm for constructing all the arrangements?

Example $\PageIndex{1}\label{eg:whatiscombo-01}$

In how many ways can five people be seated at a round table? What if a certain pair of them refuses to sit next to one another? What if there are $n$ people?

Example $\PageIndex{2}\label{eg:whatiscombo-02}$

A binary string is a sequence of digits, each of which being 0 or 1. Let $a_n$ be the number of binary strings of length $n$ that do not contain consecutive 1s. It is easy to check that $a_1=2$, $a_2=3$, and $a_3=5$. What is the general formula for $a_n$?

Example $\PageIndex{3}\label{eg:whatiscombo-03}$

The complexity of an algorithm tells us how many operations it requires. By comparing the complexity of several algorithms for solving the same problem, we can determine which one is most efficient. Let $b_n$ be the number of operations required to solve a problem of size $n$. If it is known that \[b_n = 2b_{n-1}+3b_{n-2}, \qquad n\geq3,\] where $b_1=1$ and $b_2=3$, what is the general formula for $b_n$?

Consider the number of integers from 2 to 5, inclusive. You might think there 3 integers since $5-2=3$. However, if we include the 1st and last integer, our set is $\{2,3,4,5\}$ and you can see there are 4 integers.

Theorem $\PageIndex{1}$: Counting Natural Numbers

If $m,n \in \mathbb{Z} \mbox{ and }m \geq n$ then the number of integers from $n$ to $m$ is $m-n+1$.

Example $\PageIndex{4}$

How many four-digit codes exist from $1000$ to $9999$?

Solution: $9999-1000+1=9000$ so there are $9000$ four-digit codes from $1000$ to $9999$.

Probability

Definition: Sample Space

A sample space is the set of all possible outcomes. For example, the sample space for rolling a die is:

\[1 \qquad \qquad 2 \qquad \qquad 3 \qquad \qquad 4 \qquad \qquad 5 \qquad \qquad 6\] which is the set of the six possible results from tossing a die.

Definition: Event

An event is a subset of a sample space. For example, an event for rolling two dice is: the sum is 9, i.e.

\[3\,6 \qquad\qquad 6\,3\qquad\qquad 4\,5 \qquad \qquad 5\,4\]

Definition: Probability for Equally Likely outcomes

If $E$ is an event, then the probability of that event, $P(E)$ is:

\[P(E)=\frac{\mbox{the number of outcomes in E}}{\mbox{the total number of outcomes in the sample space}}.\]

For example, there are 36 outcomes for rolling two dice, so $P(\mbox{sum of 9})= \frac {4}{36}=\frac{1}{9}.$

Since an event is a subset of the sample space, the largest number of elements in an event is the number of elements in the sample space.

Thus the maximum probability of an event is $1.$ The smallest number of elements in an event is zero, so the minimum probability of an event is $0.$

$P(E_1)=1$ means event $E_1$ will always happen.

$P(E_2)=0$ means event $E_2$ will never happen.

Example $\PageIndex{1}$

Pick a card from a standard 52-card deck. What is the probability that the number of the card is

(a) a six

(b) a number less than 20

Solution: (a) $\frac{1}{13}$

(b) $1$

(c) $0$

Pigeonhole Principle

The Pigeonhole Principle says that if you have more pigeons than pigeonholes, then at least one pigeonhole will get two pigeons.

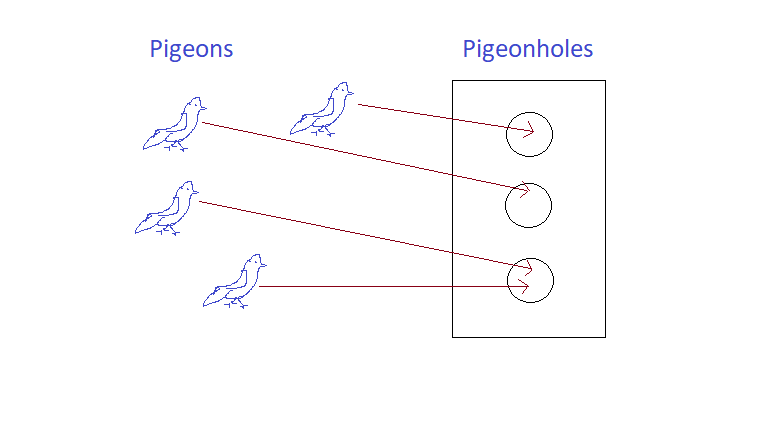
$Pigeonhole Principle.png$

If you have a function from a finite set to a smaller finite set, then the function cannot be one-to-one; in other words, there must be at least two elements in the domain with the same image in the codomain.

More formally,

Theorem $\PageIndex{2}$ Pigeonhole Principle

If $f:X \to Y$ where $X$ and $Y$ are finite sets with $|X|>|Y|$, then $f$ is not one-to-one.

Example $\PageIndex{5}$

Without looking, you pull socks out of a drawer that has just 5 blue socks and 5 white socks. How many do you need to pull to be certain you have two of the same color?

Solution: You could have two socks of different colors, but once you pull out three socks, there must be at least two of the same color.
The answer is three socks.

Example $\PageIndex{6}$

in a group of 30 people, each person picks a number from 1 to 10. What is the minimum number of people needed to be sure you have two people with the same number?

Solution: 11

Summary and Review

This chapter is about combinatorics, which is a study of arrangements of objects.
We have a theorem to find the size of a set of consecutive integers.
The probability of a event is the # of ways it can happen divided by the total # of outcomes.
Probability is a number from 0 to 1, inclusive.
The Pigeonhole Principle says if you have more pigeons than pigeonholes, at least 2 pigeons must cuddle up.

Exercises

exercise $\PageIndex{1}$

A random number is picked from 80 to 600.

(a) How many numbers are there to pick?

(b) What is the probability of picking the number 220?

Answer: (a) $600-80+1=521$ so there are 521 numbers
(b) $\frac{1}{521}$

Exercise $\PageIndex{2}$

Are you able to answer any of the 1st three examples in this section?

If so, tell your professor what you came up with. If not, look back after you have done more work in this chapter

Exercise $\PageIndex{3}$

In a group of 100 people, each person picks a number from 100 to 120. What is the minimum number of people you need to be sure two of them have the same number?

Answer: 22

Exercise $\PageIndex{4}$

In a group of 20 people, each person has one pet that is a cat, a dog or a goat. What is the minimum number of people you need to be sure two of them have the same type of pet?

Exercise $\PageIndex{5}$

How many cards do you need to pick from a standard 52-card deck to be sure to get a red card?

Answer: 27, because if you pick all of the 26 black cards, the next one must be red.

Exercise $\PageIndex{6}$

In a school of 600 students, do there have to be two students with the same birthday (month and day)? Why?

Exercise $\PageIndex{7}$

How many integers do you need to pick to be sure that at least two of them have the same remainder after dividing by 5?

Answer: 6, because there are 5 possible remainders: 0, 1, 2, 3, 4

Exercise $\PageIndex{8}$

How many cards do you need to pick from a standard 52-card deck to be sure to get two cards of the same suit?

Exercise $\PageIndex{9}$

If you pick one card from a standard 52-card deck, what is the probability it will be a diamond?

Answer: $\frac{1}{4}$

Exercise $\PageIndex{10}$

If you pick one card from a standard 52-card deck, what is the probability it will be

(a) a two or three

(b) a two and a three

Exercise $\PageIndex{11}$

If you pick one card from a standard 52-card deck, what is the probability it will be

(a) an eight or a nine or a ten?

(b) an eight and a nine?

Answer

(a) $\frac{3}{13}$

(b) $0$

Search

Text Color

Text Size

Margin Size

Font Type

Theorem \(\PageIndex{1}\): Counting Natural Numbers

Definition: Sample Space

Definition: Event

Definition: Probability for Equally Likely outcomes

Theorem \(\PageIndex{2}\) Pigeonhole Principle