0.2: Relations

Definition: Binary Relation

Let $S$ be a nonempty set. Then any subset $R$ of $S \times S$ is said to be a relation over $S$. In other words, a relation is a rule that is defined between two elements in $S$. Intuitively, if $R$ is a relation over $S$, then the statement $a R b$ is either true or false for all $a,b\in S$.

If the statement $a R b$ is false, we denote this by $a \not R b$.

Example $\PageIndex{1}$:

Let $S=\{1,2,3\}$. Define $R$ by $a R b$ if and only if $a < b$, for $a, b \in S$.

Then $1 R 2, 1 R 3, 2 R 3$ and $2 \not R 1$.

We can visualize the above binary relation as a graph, where the vertices are the elements of S, and there is an edge from $a$ to $b$ if and only if $a R b$, for $a b\in S$.

Figure $\PageIndex{1}$: Relation as a graph. (Copyright: Pamini Thangarajah)

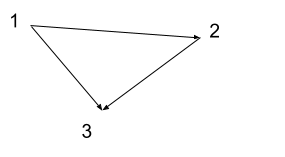
The following are some examples of relations defined on $\mathbb{Z}$.

Example $\PageIndex{2}$:

1. Define $R$ by $a R b$ if and only if $a < b$, for $a, b \in \mathbb{Z}$.
2. Define $R$ by $a R b$ if and only if $a >b$, for $a, b \in \mathbb{Z}$.
3. Define $R$ by $a R b$ if and only if $a \leq b$, for $a, b \in \mathbb{Z}$.
4. Define $R$ by $a R b$ if and only if $a \geq b$, for $a, b \in \mathbb{Z}$.
5. Define $R$ by $a R b$ if and only if $a = b$, for $a, b \in \mathbb{Z}$.

Definition: Divisor/Divides

Let $a$ and $b$ be integers. We say that $a$ divides $b$ is denoted $a\mid b$, provided we have an integer $m$ such that $b=am$. In this case we can also say the following:

• $b$ is divisible by $a$
• $a$ is a factor of $b$
• $a$ is a divisor of $b$
• $b$ is a multiple of $a$ 

If $a$  does not divide $b$, then it is  is denoted by $a \not \mid b$.

Properties of binary relation:

Definition: Reflexive

Let $S$ be a set and $R$ be a binary relation on $S$. Then $R$ is said to be reflexive if $a R a, \forall a \in S.$

 

We will follow the template below to answer the question about reflexive.

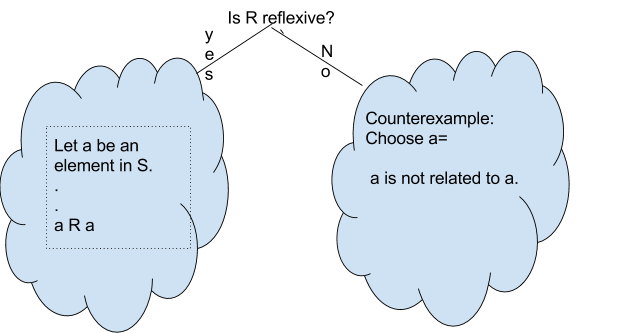
Example $\PageIndex{7}$:

Define $R$ by $a R b$ if and only if $a < b$, for $a, b \in \mathbb{Z}$. Is $R$ reflexive?

Counter Example:

Choose $a=2.$

Since $2 \not< 2$, $R$ is not reflexive.

Example $\PageIndex{8}$:

Define $R$ by $a R b$ if and only if $a \mid b$, for $a, b \in \mathbb{Z}$. Is $R$ reflexive?

Proof:

Let $a \in \mathbb{Z}$. Since $a=(1) (a)$, $a \mid a$.

Thus $R$ is reflexive. $\Box$

Definition: Symmetric

Let $S$ be a set and $R$ be a binary relation on $S$. Then $R$ is said to be symmetric if the following statement is true:

$\forall a,b \in S$, if $a R b$ then $b R a$, in other words, $\forall a,b \in S, a R b \implies b R a.$

Example $\PageIndex{8}$: Visually

$\forall a,b \in S, a R b \implies b R a.$ holds!

We will follow the template below to answer the question about symmetric.

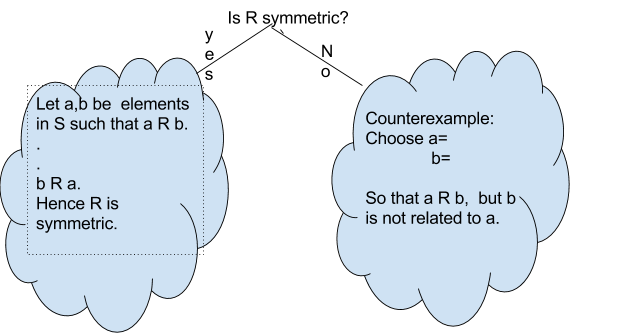
Example $\PageIndex{9}$:

Define $R$ by $a R b$ if and only if $a < b$, for $a, b \in \mathbb{Z}$. Is $R$ symmetric?

Counter Example:

$1<2$ but $2 \not < 1$.

Example $\PageIndex{10}$:

Define $R$ by $a R b$ if and only if $a \mid b$, for $a, b \in \mathbb{Z}$. Is $R$ symmetric?

Counter Example:

$2 \mid 4$ but $4 \not \mid 2$.

 

Definition: Transitive

Let $S$ be a set and $R$ be a binary relation on $S$. Then $R$ is said to be transitive if the following statement is true

$\forall a,b,c \in S,$ if $a R b$ and $b R c$, then $a R c$.

In other words, $\forall a,b,c \in S$, $a R b \wedge b R c \implies a R c$.

Example $\PageIndex{14}$: VISUALLY

$\forall a,b,c \in S$, $a R b \wedge b R c \implies a R c$ holds!

We will follow the template below to answer the question about transitive.

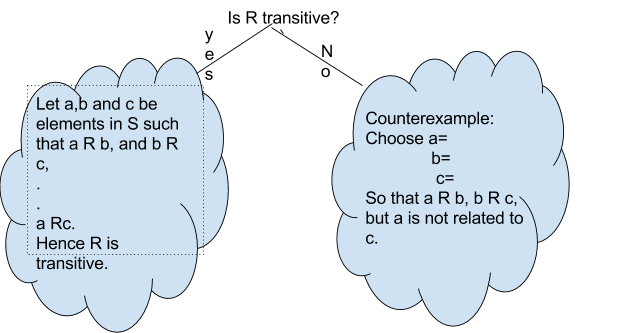
Example $\PageIndex{15}$:

Define $R$ by $a R b$ if and only if $a < b$, for $a, b \in \mathbb{Z}$. Is $R$ transitive?

Example $\PageIndex{16}$:

Define $R$ by $a R b$ if and only if $a \mid b$, for $a, b \in \mathbb{Z_+}$. Is $R$ transitive?

 

Definition: Equivalence Relation

A binary relation is an equivalence relation on a nonempty set $S$ if and only if the relation is reflexive(R), symmetric(S) and transitive(T).

Definition: Equivalence Relation

Example $\PageIndex{1}$: $=$

 

Let $S=\mathbb{R}$ and $R$ be =. Is the relation a) reflexive, b) symmetric, c) antisymmetric, d) transitive, e) an equivalence relation, f) a partial order.

Solution:

1. Yes $R$ is reflexive.

   Proof:

   Let $a \in \mathbb{R}$.

   Then $a=a$.

   Hence $R$ is reflexive. $\blacksquare$

    

   Yes $R$ is symmetric.

   Proof:

   Let $(a,b) \in \mathbb{R}$  such that $a=b.$

   Clearly $b=a$.

   Hence $R$ is symmetric. $\blacksquare$

    

Yes $R$ is antisymmetric.

Proof:

Let $a,b \in \mathbb{R}$ s.t. $a=b$ and $b=a$. Then clearly $a=b \; \forall a,b \in \mathbb{R}$. $\blacksquare$

 

Yes $R$ is transitive.

Proof:

Let $a,b,c \in \mathbb{R}$ s.t. $a=b$ and $b=c$.

We shall show that $aRc$.

Since $a=b$ and $b=c$ it follows that $a=c$

Thus $aRc$. $\blacksquare$

 

Yes $R$ is an equivalence relation.

Proof:

Since $R$ is reflexive, symmetric and transitive, it is an equivalence relation.

 

Yes $R$ is a partial order.

Proof:

Since $R$ is a partial order since $R$ is reflexive, antisymmetric and transitive.

Example $\PageIndex{2}$: Less than or equal to

Let $S=\mathbb{R}$ and $R$ be $\leq$. Is the relation a) reflexive, b) symmetric, c) antisymmetric, d) transitive, e) an equivalence relation, f) a partial order.

Solution

1. Yes, is reflexive.

Proof:

We will show that is true.

Let that is .

Since , is reflexive.◻

2. No, is not symmetric.

Counterexample:

Let and which are both .

It is true that , but it is not true that .

Thus is not symmetric.◻

3. Yes, is antisymmetric.

Proof:

We will show that given and that .

Since , s.t. .

Further, since , , .

Then .

Thus, .

Since, , thus .◻

4. Yes, is transitive.

Proof:

We will show that given and that .

Since , s.t. .

Further, since , , .

Then .

Since, , thus .◻

5. No, is not an equivalence relation on since it is not symmetric.

6. Yes, is a partial order on since it is reflexive, antisymmetric and transitive.

Definition: Equivalence Class

Given an equivalence relation $R$ over a set $S,$ for any $a \in S$ the equivalence class of a is the set $[a]_R =\{ b \in S \mid a R b \}$, that is
$[a]_R$ is the set of all elements of S that are related to $a$.

Example $\PageIndex{3}$: Equivalence relation

Define a relation that two shapes are related iff they are the same color. Is this relation an equivalence relation?

Equivalence classes are:

Example $\PageIndex{4}$:

Define a relation that two shapes are related iff they are similar. Is this relation an equivalence relation?

Equivalence classes are:

Definition: Partition

Let $A$ be a nonempty set. A partition of $A$ is a set of nonempty pairwise disjoint sets whose union is A.

 

Note

For every equivalence relation over a nonempty set $S$, $S$ has a partition.

 

Theorem $\PageIndex{1}$

If $\sim$ is an equivalence relation over a nonempty set $S$. Then the set of all equivalence classes is denoted by $\{[a]_{\sim}| a \in S\}$ forms a partition of $S$.

This means

1. Either $[a] \cap [b] = \emptyset$ or $[a]=[b]$, for all $a,b\in S$.

2. $S= \cup_{a \in S} [a]$.

Proof

Assume is an equivalence relation on a nonempty set .

Let . If , then we are done. Otherwise,

assume .

Let be the common element between them.

Let .

Then and , which means that and .

Since is an equivalence relation and .

Since and (due to transitive property), .

Thus and .

Hence .

Next, we will show that .

First we shall show that .

Let .

Then exists and .

Hence .

Thus .

Conversely, we shall show that .

Let .

Then for some .

Thus ∴ .

Thus .

Since and , then .◻

 

 

For the following examples, determine whether or not each of the following binary relations on the given set is reflexive, symmetric, antisymmetric, or transitive. If a relation has a certain property, prove this is so; otherwise, provide a counterexample to show that it does not. If is an equivalence relation, describe the equivalence classes of .

Example $\PageIndex{5}$:

Let $S = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}$. Define a relation $R$ on $A = S \times S$ by $(a, b) R (c, d)$  if and only if $10a + b \leq 10c + d.$ 

 

Solution

1. is reflexive on .

Proof:

Let .

We will show that .

Since , then .

Since is reflexive on .◻

2. is not symmetric on .

Counter Example:

Let .

Note , specifically, is true.

However, , is false.

Since , is not symmetric on .◻

3. is antisymmetric on .

Proof:

Let s.t. and .

Since and , .

We will show that and .

by definition.

Since and , thus .

Since , .

Thus is antisymmetric on .◻​​​​

5. is transitive on .

Proof:

Let s.t. and .

We will show that .

Since , .

Thus is transitive on .◻

6. is not an equivalence relation since it is not reflexive, symmetric, and transitive.

Example $\PageIndex{6}$:

Let . Define a relation on , by if and only if

Solution

1. is reflexive on .

Proof:

Let we will show that .

Clearly since and a negative integer multiplied by a negative integer is a positive integer in .

Since , is reflexive on .◻​​​​​

 

2. is symmetric on .

Proof:

We will show that if , then .

Let s.t. , that is .

Since , .

Since , is symmetric on .◻

3. is not antisymmetric on .

Counter Example:

Let and then and .

Since , is not antisymmetric on .◻

4. is transitive on .

Proof:

Let s.t and s.t. .

There are two cases to be examined:

Case 1: and .

Since , thus .

Case 2: and .

Since , thus .

Since in both possible cases is transitive on .◻

 

5. Since is reflexive, symmetric and transitive, it is an equivalence relation. Equivalence classes are and .

Let , then

.

Case 1: , then .

.

.

Case 2: , then .

.

.

Note this is a partition since or . So we have all the intersections are empty.

.

Further, we have . Note that is excluded from .

Recall:

Let $m,n \in \mathbb{Z}$.

We say that $m$ divides $n$ (written as $m|n$) if $n=mk$ for some $k\in \mathbb{Z}$.

 

Example $\PageIndex{7}$

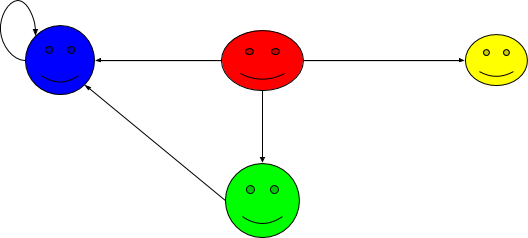
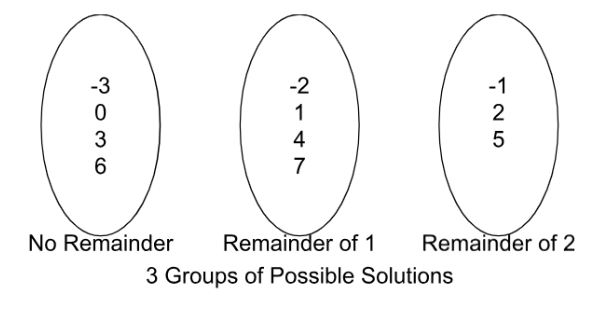
Let $S= \mathbb{Z}, m\in \mathbb{Z}_+$.  Define $aRb$ if and only if $m|(a-b), \forall a,b \in \mathbb{Z}$.

Note that $m$ is a positive integer.

Let $m=3$.  Choose $a=1$ and $b=2$.

Are 1 and 2 related? i.e. does $3|1-2$?  Does $1-2=3k, k\in \mathbb{Z}$?  Since there is no integer $k$ s.t. $-1 = 3k$, ∴ $1$ is not related to $2$.

 

However, we can see that we have three groups, as shown in the image below:

 

 

 

Definition: Modulo

Let $m$ $\in$ $\mathbb{Z_+}$.

$a$ is congruent to $b$ modulo $m$ denoted as $a \equiv b (mod \, n)$, if $a$ and $b$  have the remainder when they are divided by $n$, for  $a, b \in \mathbb{Z}$.

Properties

Let $n \in \mathbb{Z_+}$. Then

Theorem 1 :

Two integers $a$ and $b$ are said to be congruent modulo $n$, $a \equiv b (mod \, n)$, if all of the following are true:

a) $m\mid (a-b).$

b) both $a$ and $b$ have the same remainder when divided by $n.$

c) $a-b= kn$, for some $k \in \mathbb{Z}$.

NOTE: Possible remainders of $n$ are $0, ..., n-1.$

Reflexive Property

Theorem 2:

The relation " $\equiv$ " over $\mathbb{Z}$ is reflexive.

Proof: Let $a \in \mathbb{Z}$.

Then $a-a=0(n)$, and $0 \in \mathbb{Z}$.

Hence $a \equiv a (mod \, n)$.

Thus congruence modulo n is Reflexive.

Symmetric Property

Theorem 3:

The relation " $\equiv$ " over $\mathbb{Z}$ is symmetric.

Proof: Let $a, b \in \mathbb{Z}$ such that $a \equiv b$ (mod n).

Then $a-b=kn,$ for some $k \in \mathbb{Z}$.

Now $b-a= (-k)n$ and $-k \in \mathbb{Z}$.

Hence $b \equiv a(mod \, n)$.

Thus the relation is symmetric.

Antisymmetric Property

Is the relation " $\equiv$ " over $\mathbb{Z}$ antisymmetric?

Counter Example: $n$ is fixed

choose: $a= n+1, b= 2n+1$, then

$a \equiv b(mod \, n)$ and $b \equiv a (mod \, n)$

but $a \ne b.$

Thus the relation " $\equiv$ "on $\mathbb{Z}$ is not antisymmetric.

Transitive Property

Theorem 4 :

The relation " $\equiv$ " over $\mathbb{Z}$ is transitive.

Proof: Let $a, b, c \in$ $\mathbb{Z}$, such that $a \equiv b (mod n)$ and $b \equiv c (mod n).$

Then $a=b+kn, k \in$ $\mathbb{Z}$ and $b=c+hn, h \in$ $\mathbb{Z}$.

We shall show that $a \equiv c (mod \, n)$.

Consider $a=b+kn=(c+hn)+kn=c+(hn+kn)=c+(h+k)n, h+k \in$ $\mathbb{Z}$.

Hence $a \equiv c (mod \, n)$.

Thus congruence modulo $n$ is transitive.

Theorem 5:

The relation " $\equiv$ " over $\mathbb{Z}$ is an equivalence relation.

Modulo classes

Let . The relation $\equiv$ on by $a \equiv b$ if and only if , is an equivalence relation. The Classes of have the following equivalence classes:

.

 

Example of writing equivalence classes:

Example $\PageIndex{3}$:

The equivalence classes for $( mod \, 3 )$ are (need to show steps):

.

.

.

 Modulo Arithmetic

In this section, we will explore arithmetic operations in a modulo world.

Let $n \in \mathbb{Z_+}$.

Theorem 5 :

Let $a, b, c,d, \in \mathbb{Z}$ such that $a \equiv b (mod\,n)$ and $c \equiv d (mod\, n).$ Then $(a+c) \equiv (b+d)(mod\, n).$

Proof:

Let $a, b, c, d \in\mathbb{Z}$, such that $a \equiv b (mod\, n)$ and $c \equiv d (mod \,n).$

We shall show that $(a+c) \equiv (b+d) (mod\, n).$

Since $a \equiv b (mod\, n)$ and $c \equiv d (mod\, n), n \mid (a-b)$ and $n \mid (c-d)$

Thus $a= b+nk,$ and $c= d+nl,$ for $k$ and $l \in \mathbb{Z}$.

Consider$(a+c) -( b+d)= a-b+c-d=n(k+l), k+l \in \mathbb{Z}$.

Hence $(a+c)\equiv (b+d) (mod \,n).\Box$

Theorem 6:

Let $a, b, c,d, \in \mathbb{Z}$ such that $a \equiv b (mod \, n)$ and $c \equiv d (mod \,n).$ Then $(ac) \equiv (bd) (mod \,n).$

Proof:

Let $a, b, c, d \in \mathbb{Z}$, such that $a \equiv b (mod\, n)$ and $c \equiv d (mod \, n).$

We shall show that $(ac) \equiv (bd) (mod\, n).$

Since $a \equiv b (mod \,n)$ and $c \equiv d (mod\, n), n \mid (a-b)$ and $n \mid (c-d)$

Thus $a= b+nk,$ and $c= d+nl,$ for $k$ and $l \in \mathbb{Z}$.

Consider $(ac) -( bd)= ( b+nk) ( d+nl)-bd= bnl+dnk+n^2lk=n (bl+dk+nlk),$ where $(bl+dk+nlk) \in \mathbb{Z}$.

Hence $(ac) \equiv (bd) (mod \,n).\Box$

Theorem 7:

Let $a, b \in$ $\mathbb{Z}$ such that $a \equiv b (mod \, n)$. Then $a^2 \equiv b^2 (mod \, n).$

Proof:

Let $a, b \in$ $\mathbb{Z}$, and n $\in$ $\mathbb{Z_+}$, such that $a \equiv b (mod \, n).$

We shall show that $a^2 \equiv b^2 (mod \, n).$

Since $a \equiv b (mod \, n), n\mid (a-b).$

Thus $(a-b)= nx,$ where $x \in$ $\mathbb{Z}$.

Consider $(a^2 - b^2) = (a+b)(a-b)=(a+b)(nx), = n(ax+bx), ax+bx \in \mathbb{Z}$.

Hence $n \mid a^2 - b^2,$ therefore $a^2 \equiv b^2 (mod \, n).$ $\Box$

Theorem 8:

Let $a, b \in$ $\mathbb{Z}$ such that $a \equiv b (mod \, n)$. Then $a^m \equiv b^m (mod \, n)$, $\forall \in$ $\mathbb{Z}$.

Proof:

Exercise.

By using the above result, we can solve many problems. Some of them are discussed below: 

Example $\PageIndex{1}$: $mod\, 3$ Arithmetic

Let $n = 3$.

Addition

+	[0]	[1]	[2]
[0]	[0]	[1]	[2]
[1]	[1]	[2]	[0]
[2]	[2]	[0]	[1]

Multiplication

x	[0]	[1]	[2]
[0]	[0]	[0]	[0]
[1]	[0]	[1]	[2]
[2]	[0]	[2]	[1]

Example $\PageIndex{2}$: $mod\, 4$ Arithmetic

Let $n=4$.

x	[0]	[1]	[2]	[3]
[0]	[0]	[0]	[0]	[0]
[1]	[0]	[1]	[2]	[3]
[2]	[0]	[2]	[0]	[2]
[3]	[0]	[3]	[2]	[1]

Example $\PageIndex{3}$:

Find the remainder when $(101)(103)(107)(109)$ is divided by $11.$

Answer

$101 \equiv 2 (mod \, 11)$

$103 \equiv 4 (mod \, 11)$

$107 \equiv 8 (mod \, 11)$

$109 \equiv 10 (mod \,11)$.

Therefore,

$(101)(103)(107)(109) \equiv (2)(4)(8)(10) (mod \,11) \equiv 2 (mod \,11)$.

Example $\PageIndex{4}$:

Find the remainder when$7^{1453}$ is divided by $8.$

Answer

$7^0 \equiv 1 (mod \, 8)$

$7^1 \equiv 7 (mod \, 8)$

$7^2 \equiv 1 (mod \, 8)$

$7^3 \equiv 7 (mod \, 8)$,

As there is a consistent pattern emerging and we know that $1453$ is odd, then $7^{1453} \equiv 7 (mod \, 8)$. Thus the remainder is $7.$

Example $\PageIndex{5}$:

Find the remainder when $7^{2020}$ is divided by $18.$

Answer

$7^0 \equiv 1 (mod \, 18)$

$7^1 \equiv 7 (mod \, 18)$

$7^2 \equiv 13 (mod \, 18)$

$7^3 \equiv 1 (mod \, 18)$,

As there is a consistent pattern emerging and we know that $2020=(673)3+1$, $7^{2020}= 7^{(673)3+1}=\left( 7^3\right)^{673}7^1 \equiv 7 (mod \, 18).$ Thus the remainder is $7.$

Example $\PageIndex{6}$:

Find the remainder when $26^{1453}$ is divided by $3.$