3.3: Dihedral Groups (Group of Symmetries)

 Dihedral groups are an essential class of abstract algebra groups that arise naturally in geometry and other areas of mathematics.

Definition: Dihedral Groups

 Let \(n (\geq 2) \in \mathbb{Z}\) Then the Dihedral group \(D_n\) is defined by  \[ D_n=<r,s | s^2 =e, r^n=e, srs=r^{-1}>=\left\{e, r,r^2,r^3, \cdots, r^{n-1}, s, rs,\cdots, r^{n-1}s \right\}\] and, \( |D_n|= 2n.\)

Alternatively, for  \(n (\geq 3) \in \mathbb{Z}\), a dihedral group is a group of symmetries of a regular polygon with \(n\) sides. The dihedral group of order \(2n\), denoted by \(D_n\), is the group of all possible rotations and reflections of the regular \(n\) sided polygon. in this case \(r=(1,2,3,\cdots, n)\) represents a rotation of \((360/n) \) degrees clockwise about the center of the polygon, and \(s=(1,n-1)(2,n-2)(3,n-3)\cdots \) represents the rotation of 180 degrees about a line through a vertex \(n\) and the center of the figure. If \(n\) is odd, \(s\) fixes only one vertex \(n\) and if If \(n=2m\) is even, \(s\) fixes  vertices \(n\) and \(m\).

Figure \(\PageIndex{1}\): Reflections of polygons. (Copyright; Tikz Library)

Thus the group \(D_n \) consists of \(2n\) elements, which can be depicted as follows:

• \(n \) rotations, denoted by \(R_0, R_{360/n}, R_{(360)(2)/n} ..., R_{(n-1)360/n}, \) where \(R_{i (360)/n}\) represents a rotation of \((360i/n) \) degrees clockwise about the center of the polygon, for \(i=1,\cdots, n.\).
• \(n \) reflections, denoted by \(F_0, F_1, F_2, ..., F_{(n-1)},\) where \(F_i\) represents a reflection across a line passing through the center of the polygon and one of its vertices.

All rigid motions on n-gon: 

a. To replace the first vertex, we have \(n\) choices.

b. the second vertex can be replaced by \(k^{th}\) vertex by \(k+1\) or \(k-1.\)

The group operation in \(D_n,\)  is the composition of symmetries.

 

Recall from chapter 2, section 2.1 Example 11 

Example \(\PageIndex{1}\)

Consider the equilateral triangle below. What rigid motions can we make to it that will result in the triangle occupying the same space? What happens if we combine rigid motions? Keep in mind that "doing nothing" is also a rigid motion.

Symmetries of equilateral triangles: 

 

Let \(r\)  be a rotation then there are three rotations \( I, r, r^2.\) Let \(s\) be a reflection, then there are  \(s, rs, r^2s \) elements.  In this case, \( r^3=s^2=I\) and \(sr=r^2s.\) Thus \(D_3=\{I,r,r^2,s, rs, r^2s \}.\)

 

Theorem \(\PageIndex{1}\)

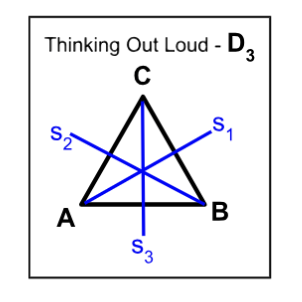Dihedral groups  \(D_n\) are non-abelian, for integers \( n ≥ 3.\)

Proof

Let \(a,b \in D_3.\)

We will show that \(ab \ne ba, \; \forall a,b \in D_n, n \ge 3.\)

\(D_3=\{e,(AB),(AC),(BC),(ABC),(ACB)\}. \)

Since \(D_3\) is isomorphic to \(S_3, D_3\)is non-abelian.

Since \(D_3 \le D_n, \forall \; n\ge 3, D_n\) is non-abelian for \(n \ge 3.\)

The Dihedral group \(D_3\) is isomorphic to \(S_3.\)

Example \(\PageIndex{2}\)

Consider the possible rotations and reflections of a  \(4\)-sided regular polygon -Square, \(D_4\).

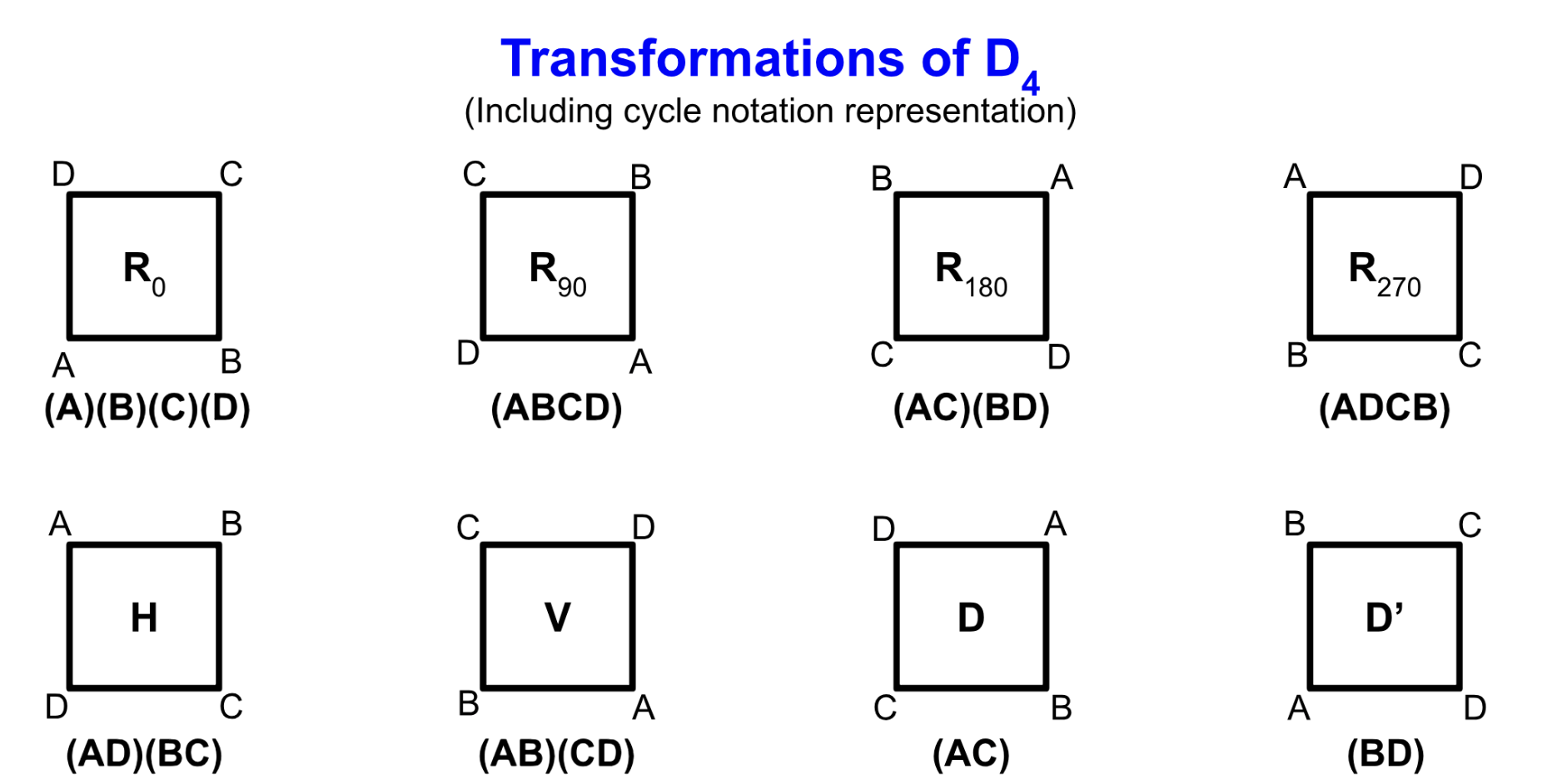
	Cayley Table for \(D_4\)
	\(R_0\)	\(R_{90}\)	\(R_{180}\)	\(R_{270}\)	H	V	D	D’
\(R_0\)	\(R_0\)	\(R_{90}\)	\(R_{180}\)	\(R_{270}\)	H	V	D	D’
\(R_{90}\)	\(R_{90}\)	\(R_{180}\)	\(R_{270}\)	\(R_0\)	D’	D	H	V
\(R_{180}\)	\(R_{180}\)	\(R_{270}\)	\(R_0\)	\(R_{90}\)	V	H	D’	D
\(R_{270}\)	\(R_{270}\)	\(R_0\)	\(R_{90}\)	\(R_{180}\)	D	D’	V	H
H	H	D	V	D’	\(R_0\)	\(R_{180}\)	\(R_{90}\)	\(R_{270}\)
V	V	D’	H	D	\(R_{180}\)	\(R_0\)	\(R_{270}\)	\(R_{90}\)
D	D	V	D’	H	\(R_{270}\)	\(R_{90}\)	\(R_0\)	\(R_{180}\)
D’	D’	H	D	V	\(R_{90}\)	\(R_{270}\)	\(R_{180}\)	\(R_0\)

 

Example \(\PageIndex{5}\)

\(D_5\) dihedral group of order \(10\), is the group of symmetries of a regular pentagon. It is composed of 10 elements, which can be represented as rotations and reflections of the pentagon.

The Cayley table for \(D_5\):

Examples abound of corporations using Dihedral groups, \(D_n,\) as their logos. Below are examples of \(D_1, D_3, \) and \(D_5.\)

 

Example \(\PageIndex{6}\)

Consider the Dihedral group \(D_4\).  \(D_4=<r,s|r^4=e, s^2=e, srs=r^{-1}>\).

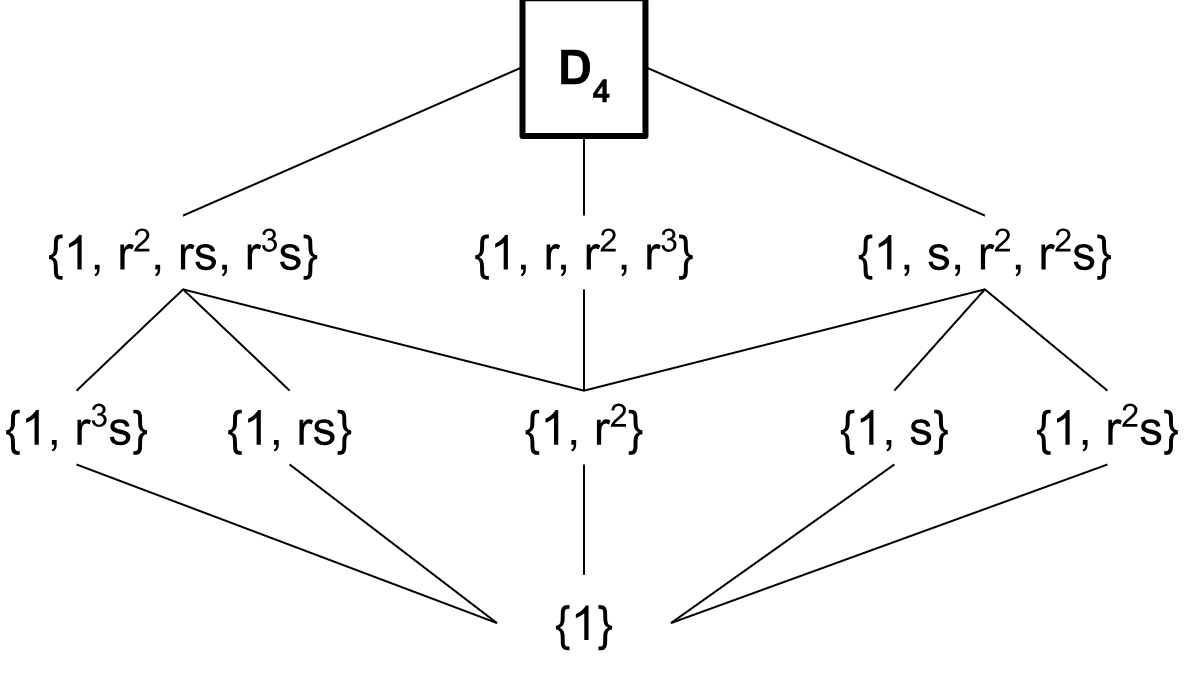
1. Find all the subgroups lattice of \(D_4\), the Dihedral group of order 8.

\(D_4=\{1,r,r^2,r^3,s,rs,r^2s,r^3s\}\). Thus, the subgroup lattice would look like this:

2. Prove that every subgroup of \(D_4\) of odd order is cyclic.

Proof:

We shall show that all odd subgroups of \(D_4\) are cyclic.

The only possible odd subgroup, which is cyclic, is \(\{e\}\).  

Thus, every subgroup of \(D_4\) of odd order is cyclic.◻

Theorem \(\PageIndex{2}\)

Let the group \(D_n=<r,s|r^n=e, s^2=e,srs=r^{-1}>\).

1. Then  \(r^ks=sr^{-k}\).

Proof

Consider \(r^ks=er^ks=s^2r^ks=ssr^ks=sr^{-k}.\)

2. The order of \(r^k\) is \(\frac{n}{\gcd(k,n)}\).

Proof

We will first show that \(r^k=e\)  if and only if \(n|k\).

Consider \(e=r^k\). 

Then by the division algorithm, \(k=na+b\) where \(0 \le b < n\).

Thus \(e=r^k=r^{na+b}=r^{na}r^b=er^b=r^b\).

Since the smallest possible integer, \(m\), such that \(r^m=e\) is \(n\), \(b=0\).

Conversely, if \(n|k\), then \(k=ns, s \in \mathbb{Z}\).

Thus \(r^k=r^{ns}=(r^n)^s=e^s=e\).

Thus \(r^k=e\) iff \(n|k\).

Let \(b=r^k, \in D_4\) since \(r\) is a generator of \(D_n\).

We shall show that the smallest integer, \(m\) s.t. \(r^k=e\) is \(\frac{n}{k}\).

Let \(d=\gcd(n,k)\).

Consider \(e=b^m=r^{km}\).

Since this is the smallest integer \(m\) such that \(n|km\).  Thus \(\frac{n}{d}|m(\frac{k}{d})\).

Since \(d\) is the greatest common divisor of \(n\) and \(k\), \(\frac{n}{d}\) and \(\frac{k}{d}\) are relatively prime.

Hence \(\frac{n}{d}|m(\frac{k}{d})\) means that \(\frac{n}{d}|m\).  The smallest such \(m\) is \(\frac{n}{d}\).

Thus \(|r^k|= \frac{n}{\gcd(n,k)}\).◻

Example \(\PageIndex{7}\)

Find the centre of \(D_n\).

Solution:

Let \(D_n=<r,s|r^n=e, s^2=e,srs=r^{-1}>\)

We shall show that,

\(Z(D_n) = \{x \in D_n \mid dx = xd, \forall d \in D_n\} = \begin{cases}
\{e\}, & \text{if } n \text{ is not divisible by } 2 \\
\{e, r^2\}, & \text{if } n \text{ is divisible by } 2
\end{cases}\)
 

Let's consider an element \(x\) in \(D_n \) that commutes with every other element in the group. Therefore, any element in \(D_n \) that commutes with every other element is either the identity element e or a rotation \(r^k \) where \(k\) is a multiple of \(n/2 \) (for even \(n\)).

• If \(x\) is the identity element \(e\), it commutes with every element and is in the center.
• If \(x \) is a rotation \(r^k,\)  where \(k\) is a multiple of \(n/2\)) (for even \(n\)), or \(x\) is the identity element e (for odd \(n\)), then it commutes with every element, and it is in the center.
• If \(x\) is a rotation \(r^k,\)  where \(k\) is not a multiple of \(n/2\)(for even \(n\)), then it commutes with all rotations but not with reflections. Therefore, it cannot commute with every element and is not in the center.

By combining these two statements, we can conclude that the center of \(D_n\) consists of the identity element e and the rotation \(r^{n/2}\) (if \(n\) is divisible by \(2\)), or just the identity element \(e\) (if \(n\) is not divisible by \(2\)) for even \(n\). For odd \(n\), the center consists only of the identity element \(e.\)