5.1: Introduction to Rings

Recall a group is a set with a binary operation; rings are algebraic structures similar to groups but with two operations instead of one.

Definition: Ring

A non-empty set $R$ with two binary operations, addition and multiplication - denoted by $+$ and $\cdot$, is called a ring if:

1. $(R,+)$ is an abelian group .

2.  $(R,\cdot)$ is a semigroup: $a \cdot b \in R, \;\forall a,b \in R$ and $a \cdot (b \cdot c)=(a \cdot b) \cdot c, \; \forall a,b,c \in R$.  $R$ in this context is a ring.

3.  Multiplication distributes over addition: $a \cdot (b+c)=a \cdot b+a \cdot c$ and $(b+c)\cdot a=b \cdot a+c \cdot a$, $\forall a,b,c \in R$.  (Distributive property).

Note

We call the additive identity $0$ is zero. The additive inverse is called the negative element.

$\{0\}$ is a ring called zero ring.

In this chapter, we will  denote $a \cdot b$ as $ab$ (skipping the $\cdot$ notation).

 

Definition: Commutative Ring 

A ring $(R, +, \cdot)$ is called a commutative ring if $ab=ba, \; \forall a,b \in R$.

Definition: Unity

A ring $(R, +, \cdot)$ has a unity(identity) $e \in R$ if $ae=ea=a, \; \forall a \in R$.  Note unity is always a unique, single element.

Definition: Unit 

An element $a\in R$ is called a unit if there exists an $a^{-1}\in R$ s.t. $aa^{-1}=e$.

Example $\PageIndex{1}$

1. $(\mathbb{Z},+, \cdot)$ is a commutative ring with unity $1$.

2. $(\mathbb{Z}_n,\bigoplus, \bigodot)$ (modulo n addition and multiplication) is a commutative ring with unity $1$ and units of $U(n)$ since they must be all the elements relatively prime to n.

3. $(\mathbb{Z}_{[x]}, +, \cdot)$ where $\mathbb{Z}_{[x]}$ is the set of all integer polynomials in variable $x$, is a commutative ring with unity of $1$ and units of $\pm 1$.

4. $(M_{22}(\mathbb{Z}), +, \cdot)$ is a ring, from the set of all $2 \times 2$ matrices with integer entries, that has unity $I$.  It is a non-commutative ring.  The units are the set of all $2 \times 2$ matrices with a non zero determinant  $(GL_2(\mathbb{Z}))$.

5.  $(\mathbb{Q}, +, \cdot)$ is  a field.It is a commutative ring with unity $1$ and  each $a \in \mathbb{Q} \setminus \{0\}$ is a unit.

6. $(\mathbb{R}, +, \cdot)$ is  a field.  It is a commutative ring, and inverses exist for all elements except 0.

7. $(\mathbb{C}, +, \cdot)$ is also a field, and inverses exist for all elements except 0.

8. A polynomial ring $R[x]$  over a ring $R$ is defined as $\{(p(x)=a_0+a_1x+\cdots+a_nx^n \mid n \in \mathbb{Z}, n\geq 0, a_i \in R, \forall i=1, \cdots, n\}$. Where $a_i$  is the coefficient of $x^i$, also called the coefficients of the polynomial, and the non-negative integer $n$ is called the degree of the polynomial.

The coefficients $a_i$ can be elements from any ring, such as integers, rational numbers, real numbers, complex numbers, or even other polynomials. The addition and multiplication  of $R[x]$ are the addition and multiplication $R.$

 

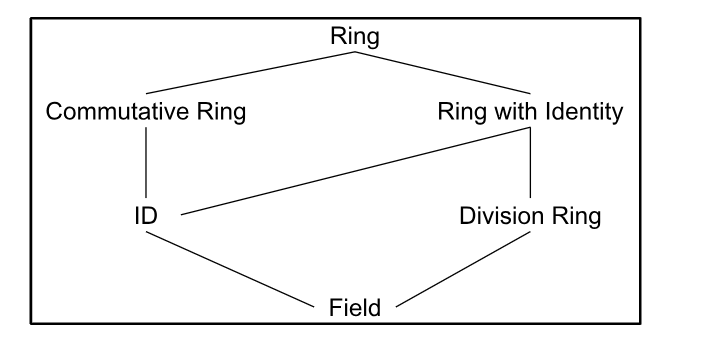
Integral Domain (ID)

 Recall: $(R,+,\cdot)$ is a non-empty set with closed binary operations.

$(R,+)$ is abelian.

$(R,\cdot)$ is a semigroup.  Recall that this is a set with an associative operation and no identity.

$(R,+,\cdot)$ is distributive, has unity (aka identity) of $1$ and unit of $aa^{-1}=e$

If $ab=ba$, the ring is commutative on $\cdot$.

Definition:  Integral Domain

A commutative ring with unity (aka identity), $R$, is called an integral domain if for every $a,b \in R$, $ab=0$ implies $a=0$ or $b=0$.

 

Example $\PageIndex{2}$

Examples of non-integral domains:

1. In the ring $\mathbb{Z}_6$ (integers modulo 6), $2 \cdot 3 = 6 \equiv 0 \pmod{6}$, but neither 2 nor 3 is zero in $\mathbb{Z}_6$.

2.  In the ring $(M_{22}(\mathbb{Z}), +, \cdot)$;

$\begin{bmatrix} 1 & 0 \\0 & 0 \end{bmatrix} \begin{bmatrix} 0 & 0 \\0 & 1 \end{bmatrix}=\begin{bmatrix} 0 & 0 \\0 & 0 \end{bmatrix}$, but neither $\begin{bmatrix} 1 & 0 \\0 & 0 \end{bmatrix}$ nor $\begin{bmatrix} 0 & 0 \\0 & 1 \end{bmatrix}$ equal zero.

Definition: Division Ring

A division ring is a ring, (R), with an identity in which for every non-zero $a \in R$, there exists $b \in R$ s.t. $ab=1=ba$.

 

Example $\PageIndex{3}$

Examples of division rings:

$(\mathbb{Q},+,\cdot)$, $(\mathbb{R},+,\cdot)$, and $(\mathbb{C},+,\cdot)$,  $\mathbb{Z}_p$, where $p$ is  prime.

 

Definition: Field

A field is a commutative division ring.

 

Example $\PageIndex{4}$

Examples of fields are:  $(\mathbb{Q},+,\cdot)$, $(\mathbb{R},+,\cdot)$, $\mathbb{Z}_p$, where $p$ is  prime,

and $(\mathbb{C},+,\cdot)$, with the later being algebraically closed.

Definition: Zero divisor

A non-zero element of $a \in R$ is called a zero divisor if there exists $ab \in R$ s.t. $ab=0$.

Example $\PageIndex{5}$

$(\mathbb{Z},+,\cdot)$.

Since there are no zero divisors, it is an integral domain.   It is a commutative ring.  Not every non-zero element is a unit. Thus, it is not a field.

Example $\PageIndex{6}$

$(\mathbb{Z}_n,\oplus,\odot)$.

There are two cases. 

This is a finite field if $n$ is prime.

If $n$ is not prime, it is not an integral domain since it will have a zero divisor.

Example $\PageIndex{7}$

The set of all real-valued differentiable functions on $[a,b]$ is a commutative ring with a unit.  This area of study is called differential algebra.

Example $\PageIndex{8}$

$M_{22}(\mathbb{R},+,\cdot))$.

The addition is abelian.  It is not commutative.  It has an identity. It's not an integral domain.

This area of study is called matrix algebra.

 

Example $\PageIndex{9}$

 Let 

$1=\begin{bmatrix} 1 & 0 \\0 & 1 \end{bmatrix}, I= \begin{bmatrix} 0 & 1 \\-1 & 0 \end{bmatrix}, J= \begin{bmatrix} 0 & i \\i & 0 \end{bmatrix}, K= \begin{bmatrix} i & 0 \\0 & -i \end{bmatrix}$. 

In other words, $I^2=J^2=K^2=IJK=-1.$

Define 

$\mathbb{H}= \{ a+bI+cJ+dK  \mid a,b,c,d \in \mathbb{R} \}.$ Then $\mathbb{H}$ is Ring of Quaternions which is a division ring but not a field.

* discovered by Hamilton in 1843.

Example $\PageIndex{10}$

Let 

$\mathbb{H}= \left \{ \begin{bmatrix} a & b \\- \bar{b} & \bar{a} \end{bmatrix}  \mid a, b \in \mathbb{C} \right\}.$ 

 

 Then  $\mathbb{H}$ is a division ring with matrix addition and multiplication, but not an integral domain.

Properties of Rings

Theorem $\PageIndex{1}$: Cancellation Law

Let $D$ be a commutative ring with identity. Then $D$ is an integral domain if and only if $ab=bc$ implies $b=c\; \forall a,b,c \in D$. 

Theorem $\PageIndex{2}$

Let $(R,+, \cdot)$ be a ring and $a,b \in R$.

1. $a0=0=0a$.

2. $a(-b)=(-a)b=-ab$.

3. $(-a)(-b)=(ab)$.

Answer

 

1. Let $a \in R.$ Then $0 a=(0+0) a=0a+0a. \implies 0a+0=0a+0a.$ By cancellation law of $+$, we get $0a=0.$ Similarly, we can show that $a 0=0.$

2. Let $a, b \in R.$ Then $ab+(-a)b=(a+(-a))b=0 b=0. \implies (-a)b=-(ab).$ Similarly, $ab+a(-b)=a(b+(-b))=a 0=0. \implies a(-b)=-(ab).$ 

 

Subring:

Let $(R,+,\cdot)$ be a ring.

Let $S(\ne 0) \subseteq R$.

Then $S$ is a subring of $R$ if $(S,+,\cdot)$ is a ring with the same operations.

Theorem $\PageIndex{3}$

Subring Test

Let $(R,+,\cdot)$ be a ring.

$S \subseteq R$ is a subring if and only if the following conditions are satisfied:

1. $S \ne \{\}$.  At least $0\in S$.

2. $a-b\in S$. 

3. $ab \in S, \; \forall a,b \in S$.

Example $\PageIndex{11}$

Let $(R,+,\cdot)$ be a ring then $\{0\}$ and $R$ are subrings of $R$ and are called the trivial subrings of $R$.

Example $\PageIndex{12}$

Let $(\mathbb{Q},+, \cdot)$ is a subring of $(\mathbb{R},+, \cdot)$ and $(\mathbb{R},+,\cdot)$ is a subring of $(\mathbb{C},+,\cdot)$.

 

Example $\PageIndex{13}$

$(\mathbb{Z}_6,\oplus, \odot)$ is a ring.

1.  Let $S=\{0, 3 \}$.

Clearly, $S$ is non-empty.

Since $0\oplus 3$, $0 \oplus0$, and $3 \oplus3$, $a-b \in S$.

Since $0\odot3$, $0 \odot 0$, and $3 \odot 3$, then $ab \in S$ .

Thus $S$ is a subring of $(\mathbb{Z}_6,\oplus, \odot)$.

2. 

Let $T =\{0, 2, 4 \}$.

Clearly, $T$ is non-empty.

Since $0 \oplus 0$, $0 \oplus 2$, $0 \oplus 4$, $2 \oplus 2$,$2 \oplus 4$ and $4 \oplus 4\in T$ then $a-b \in T$

Since $0 \odot 0$,  $0 \odot 2$,  $0 \odot 4$,  $2 \odot 2$,  $2 \odot 4$, and  $4 \odot 4 \in T$, then $ab \in T$.

Thus $T$ is a subring of  $(\mathbb{Z}_6,\oplus, \odot)$.

Example $\PageIndex{14}$

Define $\mathbb{Z}[i]=\{ m+ni|m.n \in \mathbb{Z}\},$ where $i^2=-1.$

This is a ring called Gaussian integers. The units of this ring are $\pm1$ and $\pm i$. Hence  The ring of Gaussian integers is not a field.This is a subring of $(\mathbb{C},+,\cdot ).$

 

Theorem $\PageIndex{4}$: Wedderburn's Theorem

Every finite integral domain is a field.

Answer

Let $D$ be a finite integral domain.

Let $D^{*} = D \backslash \{0\}$.

We shall show that every element in $D^*$ is a unit (i.e., $aa^{-1}=e,\; \forall a \in D^*$).

Let $a\in D^*$.

Define $\lambda_a : D^* \rightarrow D^*$ by $\lambda_a(x)=ax, \; x\in D^*$.

We shall show that $\lambda_a$ is injective.

Let $x_1, x_2 \in D^*$ s.t. $\lambda_a(x_1)=\lambda_a(x_2)$.

Consider $ax_1=ax_2$.

Thus $ax_1-ax_2=0$.

So $a(x_1-x_2)=0$.

Since $D$ is an integral domain, either $a=0$ or $(x_1-x_2)$=0\).\)

Since $D^*$ excludes zero, $a \ne 0$.

Thus $x_1-x_2=0$.

Hence $x_1=x_2$ and $\lambda_a$ is injective.

 

Since $D$ and $D^*$ are finite, $\lambda_a$ is surjective.

Since $1 \in D^*, \; \exists x \in D^*$ s.t. $\lambda_a(x)=1$.

Thus, $a$ is a unit, and therefore, it is a field

Characteristic of a ring R

Definition: Characteristic

Let $r \in R$, then $r+r=2r, r+r+r=3r, \cdots, r+ \cdots+ r =nr.$

The characteristic of a ring $R$  is the least positive integer $n$ such that $nr=0, \forall r \in R.$ If no such $n$ exists, we say that the characteristic of ring $R$ is $0.$

Example $\PageIndex{15}$

1. $( \mathbb{Z}, + \cdot),  ( \mathbb{Q}, + \cdot),  ( \mathbb{R}, + \cdot),  ( \mathbb{C}, + \cdot)$ are rings of characteristic $0.$

2. $(\mathbb{Z}_6,\oplus, \odot)$ is a ring of characteristic $6.$

Theorem $\PageIndex{5}$

1. Let $R$ be ring with identity $1.$ If $n$ is the least positive integer such that $n1=0,$ then the characteristic of ring R is $0.$

2. The characteristic of an integral domain is  either prime or $0.$