Assignment 6

Exercise \(\PageIndex{1}\)

1. Find subgroups \( H \) and \( K \) of \( D_4 \) such that \( K \) is normal to \( H \) and \(H\) is normal to \(D_4\) but  \( K \) is not normal to \(D_4\). 
2. Find subgroups \( H \) and \( K \) of \( S_4 \) such that \( K \) is normal to \( H \) and \(H\) is normal to \(S_4\) but  \( K \) is not normal to \(S_4.\)
3. Prove or disprove: If all the subgroups of a group \(G\) are normal subgroups of \(G\), then \(G\) is abelian.

Answer

1.  Let \(G= D_4 = \{e, r, r^2, r^3, s, sr, sr^2, sr^3\}\) with \(r^4=4, s^2=e\) and \(srs=r^{-1}\). Since \(|D_4|=8\), possible order of subgroups are \(1,2,4\) and \(8\). Let \(H=\{1,r^2,s, sr^2\}.\) We shall show that \(H\) is normal to \(D_4.\) Consider the following Cayley table for \(H\),

Table \(\PageIndex{1}\): Cayley Table

	\(e\)	\(r^2\)	\(s\)	\(sr^2\)
\(e\)	\(e\)	\(r^2\)	\(s\)	\(sr^2\)
\(r^2\)	\(r^2\)	\(e\)	\(sr^2\)	\(s\)
\(s\)	\(s\)	\(sr^2\)	\(e\)	\(r^2\)
\(sr^2\)	\(sr^2\)	\(s\)	\(r^2\)	\(e\)

Hence, \(H \leq G.\)  By Lagranges Theorem, \([G:H] = \frac{|G|}{|H|} = 2, gH = Hg, \forall\ g\in G\). Thus, \(H \trianglelefteq G\).

Choose \(K= \{e,s\}. \) We shall show that \( K \) is normal to \( H \) and \(K\) is not normal to \(D_4.\)  Consider the following Cayley table for \(H\),

Table \(\PageIndex{2}\): Cayley Table

	\(e\)	\(s\)
\(e\)	\(e\)	\(s\)
\(s\)	\(s\)	\(e\)

Clearly  \(K\leq G\) and \(K\le H.\) \(\text{Since }[H:K] = 2 \text{, then } hK = Kh, \forall\ h\in H\). Therefore \( K \trianglelefteq H \). Let  \(k = s \in K \) and \(g = r  \in G\). Consider \(gkg^{-1} = rsr^{-1} = sr^{-1}r^{-1} = sr^{-2} = sr^2 \notin K\). Thus \(K\ntrianglelefteq G.\)

2. Let \(G = S_4, H= K_4 = \{e,(12)(34), (13)(24), (14)(23)\}\) and \(K=\{e, (12)(34)\}.\) Consider the Cayley table for \(H\) and \(K\),

 

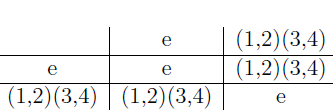
Then clearly, \(H\leq G \text{, } K\leq G.\) We shall show that \(H \trianglelefteq G\) and \(K \trianglelefteq H\).

By Lagrange's Theorem, \([H:K] = \frac{|H|}{|K|} = 2, gK = Kg, \forall\ g\in H\). Thus, \(K \trianglelefteq H\).   

Now, by Lagrange's Theorem, \([G:H] = \frac{|G|}{|H|} = \dfrac{24}{4}=6\), Hence \(H\) has \(6\) cosets in \(G\).

 Now, consider the left cosets of \( H\) in \(G\):\[ eH = \{ ee, e(12)(34), e(13)(24), e(14)(23) \}  = \{ e, (12)(34), (13)(24), (14)(23) \} \] \[ = ((1, 2)(3, 4))H = ((1, 3)(2, 4))H  = ((1, 4)(2, 3))H. \] \[ (1, 2, 3)H = \{ (1, 2, 3)e, (1, 2, 3)(12)(34), (1, 2, 3)(13)(24), (1, 2, 3)(14)(23) \} = \{ (1, 2, 3), (1, 3, 4), (2, 4, 3), (4, 2, 1) \} = (1, 3, 4)H  = (2, 4, 3)H  = (4, 2, 1)H .\] \[ (3, 2, 1)H= \{ (3, 2, 1)e, (3, 2, 1)(12)(34), (3, 2, 1)(13)(24), (3, 2, 1)(14)(23) \}  = \{ (3, 2, 1), (2, 3, 4), (1, 2, 4), (1, 4, 3) \} = (2, 3, 4)H = (1, 2, 4)H = (1, 4, 3)H. \] \[ (12)H= \{ (12), (34), (1324), (1243) \}. \] \[ (13)H = \{ (13), (24), (1423), (1234) \}. \]\[ (14)H = \{ (14), (23), (1342), (1432) \}. \]

And the right cosets of \( H \) are: \[ He = \{ ee, (12)(34)e, (13)(24)e, (14)(23)e \}  = \{ e, (12)(34), (13)(24), (14)(23) \}  = H((1, 2)(3, 4))  = H((1, 3)(2, 4)) = H((1, 4)(2, 3)) \] \[ H(1, 2, 3) = \{ e(1, 2, 3), (12)(34)(1, 2, 3), (13)(24)(1, 2, 3), (14)(23)(1, 2, 3) \}  = \{ (1, 2, 3), (2, 4, 3), (1, 4, 2), (1, 3, 4) \} = H(1, 3, 4)= H(2, 4, 3)= H(1, 4, 2) \] \[ H(3, 2, 1) = \{ e(3, 2, 1), (12)(34)(3, 2, 1), (13)(24)(3, 2, 1), (14)(23)(3, 2, 1) \}  = \{ (3, 2, 1), (1, 4, 3), (2, 3, 4), (1, 2, 4) \} = H(2, 3, 4)  = H(1, 2, 4)  = H(1, 4, 3) \]\[ H(12)= \{ (12), (34), (1324), (1243) \}. \] \[H (13)= \{ (13), (24), (1423), (1234) \}. \]\[H (14)= \{ (14), (23), (1342), (1432) \}. \]

Since the right cosets are the same as the left cosets, we know that \( H \) is normal in \( G \).

We shall show that \(K\) is not a normal subgroup of \(S_4.\) Since \((1, 2, 3)(12)(34)(3,2,1)=(1,3)(2,4)\notin K\), \(K\) is not a normal subgroup of \(S_4.\)

3. Consider \(G=Q_8=\{1, -1, i, -i, j, -j, k, -k\}\). Then, by Lagrange's theorem, possible orders of subgroups of \(Q_8\) are \(1, 2, 4\) and \(8\). The trivial subgroups  \(Q_8\) and \(\{e\}\) of order \(8\) and \(1\) are normal subgroups of \(G\). Let \(H\) be a subgroup of order \(4\). Then, by Lagrange's Theorem, \([G:H] = \frac{|G|}{|H|} = \dfrac{8}{4}=2.\) Hence the subgroups of order \(4\) (namely \(H_1 =\{1, -1, i, -i\}, H_2=\{1, -1, j, -j\}, H_3 =\{1, -1, k, -k\}\)) are normal subgroups of \(G\). Consider the subgroups of order \(2\), \(\langle -1\rangle= Z(Q_8)\). Hence, the subgroup of order \(4\) is a normal subgroup of \(G\). Therefore, all subgroups of \(G\) are abelian. However, since \(ij =k \ne -k= ji\),  \(G\) is not abelian.

Exercise \(\PageIndex{2}\)

1.  Let \(G=<a>\) where   \(|a|=12,\) and let \(H=<a^4>.\) Find all cosets in \(G/H\) and  write down the Cayley table. Is \(G/H\) cyclic? Why or why not?
     Find the cosets in \(D_6/Z(D_6),\) write down the Cayley table of  \(D_6/Z(D_6).\)  Is \(D_6/Z(D_6)\) cyclic, why or why not?

Answer

1. Let \(G = \langle a\rangle\) and let \(H = \langle a^4\rangle\). Then, \(|H|=\dfrac{12}{gcd(12,4)}=\dfrac{12}{4}=3.\) Hence, by Lagrange's Theorem. \([G:H] = \frac{|G|}{|H|} = \dfrac{12}{3}=4\), Hence \(H\) has \(4\) cosets in \(G\).

First, let's find all elements in \(G/H\).

\begin{align*}G &= \{a, a^2, \dots\ a^{10}, a^{11}, e\}\\H &= \{a^4, a^8, e\}\\&eH = \{a^4, a^8, e\} = a^4H = a^8H\\&aH = \{a, a^5, a^9\} = a^5H = a^9H\\&a^2H = \{a^2, a^6, a^{10}\} = a^6H = a^{10}H\\&a^3H = \{a^3, a^7, a^{11}\} = a^7H = a^{11}H\\G/H &= \{H, aH, a^2H, a^3H\}\end{align*}

From the table, \(G/H = \langle aH \rangle\). Hence \(G/H\) is a cyclic group.

2. Find the cosets in \(D_6/Z(D_6),\) write down the Cayley table of \(D_6/Z(D_6).\) Is \(D_6/Z(D_6)\) cyclic, why or why not?

Answer

Find all the cosets in \(D_6/Z(D_6):\) 

Let \( G = D_6 = \{e, r, r^2, r^3, r^4, r^5, s, sr, sr^2, sr^3, sr^4, sr^5\} \) and let \( H = Z(D_6) = \{e, r^3\}.\) Then \( D_6 / Z(D_6) = \{gZ(D_6)| g\in G\}\).

Index of \( Z(D_6) \) in \( D_6 \)} The index of \( Z(D_6) \) in \( D_6 \) is calculated as follows: \[ [D_6 : Z(D_6)] = \frac{|D_6|}{|Z(D_6)|} = \frac{12}{2} = 6. \] Therefore, the factor group \( D_6 / Z(D_6) \) has 6 elements. 

\begin{align*}&er^3 = r^3, && r^3r^3 = r^6 = e, &&\{e, r^3\} = eH = r^3H\\&rr^3 = r^4, && r^4r^3 = r^7 = r, &&\{r, r^4\} = rH = r^4H\\&r^2r^3 = r^5, && r^5r^3 = r^8 = r^2, &&\{r^2, r^5\} = r^2H = r^5H\\&sr^3 = sr^3, && sr^3r^3 = sr^6 = s, &&\{s, sr^3\} = sH = sr^3H\\&srr^3 = sr^4, && sr^4r^3 = sr^7 = sr, &&\{sr, sr^4\} = srH = sr^4H\\&sr^2r^3 = sr^5,&& sr^5r^3 = sr^8 = sr^2, &&\{sr^2, sr^5\} = sr^2H = sr^5H\\ \end{align*}

Is \( D_6 / Z(D_6) \) Cyclic?

 We analyze the orders of the elements of \( D_6 / Z(D_6) \): \[ | \langle eZ(D_6) \rangle | = 1, \quad | \langle rZ(D_6) \rangle | = 3, \quad | \langle r^2Z(D_6) \rangle | = 3, \] \[ | \langle sZ(D_6) \rangle | = 2, \quad | \langle rsZ(D_6) \rangle | = 2, \quad | \langle r^2sZ(D_6) \rangle | = 2. \] Thus, \( D_6 / Z(D_6) \) has no elements of order 6, and therefore, it has no possible generators. Hence, \( D_6 / Z(D_6) \) is not a cyclic group.

 

3. Prove or disprove the following statements:  If \(H \) is a normal subgroup of \(G\) such that \(H\) and \(G/H\) are abelian, then 
\(G\) is abelian.

Answer

Counterexample:  Let \( G = S_3 \) and \( H = A_3 \). Then \[ |G / H| = [G : H] = 2. \] Thus, \( H \) is a normal subgroup of \( G \), and \( G / H \) is cyclic. Clearly, \( A_3 \) is also cyclic. Therefore, both \( G / H \) and \( H \) are abelian. However, \( S_3 \) is not abelian.

Exercise \(\PageIndex{3}\)

1. Let \(G\) be a group. Show that the center of the group \(Z(G)\) is a normal subgroup of \(G.\)
2. If \(G/Z(G)\)  is cyclic , then \(G\) is abelian.
3. Let \(G\) be a non-ablian group of order \(pq\), where \(p\) and \(q\) are prime. Then the center of \(G\), \(Z(G)=\{e\}.\)

Answer

1. First we shall show that \(Z(G)\) is a subgroup of \(G.\) Since \(e\in G\) and \(eg=ge\), \(\forall g \in G.\) Thus \(e \in Z(G).\) Let \(g_1,g_2\in Z(G)\). Then \(g_1g=gg_1, g_2g=gg_2\) for all \(g\in G.\)

Let \(g\in G.\) Consider \( g(g_1g_2)=( gg_1)g_2= (g_1g)g_2= g_1(gg_2)= g_1(g_2g)= (g_1g_2)g.\) Thus \( (g_1g_2\in Z(G).\)

Since \(g_1g=gg_1\), \(g_1^{-1}( g_1g)=g_1^{-1}(gg_1) \implies g g_1^{-1}=g_1^{-1}g. \) Thus \( g_1^{-1}\in Z(G).\) Thus \(Z(G)\) is a subgroup of \(G.\)

Since \(g_1 \in Z(G),\) \(g^{-1} g_1g= g_1 \in Z(G).\) Thus \(g^{-1} Z(G) g \subset Z(G).\) Hence \(Z(G)\) is a normal subgroup of \(G.\)

2. Suppose \( G / Z(G) \) is cyclic. Then \( G / Z(G) =\langle (gZ(G))\rangle, \) for some \(g \in G.\) Let \(g_1,g_2 \in G\) Then \(g_1 Z(G)= g^m Z(G), \quad g_2 Z(G)= (gZ(G))^n = g^n Z(G), \) for  some \( m, n \in \mathbb{Z} \). Thus \( g_1 = g^m f_1, \quad g_2 = g^n f_2, \) for some \( f_1, f_2 \in Z(G) \). Now consider: \[ g_1 g_2 = g^m f_1 g^n f_2, \] \[ = g^m g^n f_1 f_2, \] \[ = g^{m+n} f_1 f_2, \] \[ = g^{n+m} f_1 f_2, \] \[ = g^n f_2 g^m f_1, \] \[ = g_2 g_1. \] Thus, \( g_1 g_2 = g_2 g_1 \), which shows that \( G \) is abelian.

3. Let \(H := Z(G)\). Since \(H \leq G\), by Lagrange's Theorem (Theorem 4.1.4), we know that \(|H|\mid |G| \). Hence the potential values of \(|H|\) are \( 1, p, q, pq\). Let's consider each.

Case 1:\(|H| = pq\),  If \(|H| = pq\) then \(|H| = |G|\), and \(H = G\). This would mean that \(G = Z(G)\), but since \(G\) is non-abelian, this is a contradiction. Therefore, \(|H| \neq pq\).

Case 2:\(|H| = p\) or \(|H| = q\). This means that \(H\) is of prime order, and by the previous problem, this implies that \(G\) is abelian. Again, this is a contradiction. Therefore \(|H| \neq p\) and \(|H| \neq q\). 

Therefore, if \(G\) is a non-abelian group of order \(pq\), then \(Z(G) = \{ e\}\).

Exercise \(\PageIndex{4}\)

1.  Let  \(h: G\to G_1\) be a group homomorphism. If  \(K\) is normal to subgroup of \(G,\) then show that \(h(K)\) is a normal subgroup of \(h(G).\)
2.  If \(h_1: G\to G_1\) is  a group homomorphism and \(G=\langle X\rangle\) is generated by a subset \(X\), then  show that \(h=h_1\) if and only if   \(h(x)=h_1(x), \forall x\in X.\)
3.   Show that there are almost six  homomorphisms from \(S_3\) to a cyclic group of order \(6\), \(\mathbb{Z}_6\).

Answer

1. Let \(k_1, k_2 \in K\), then since \(K\) is a subgroup of \(G\),  then \(h(k_1k_2) = h(k_1)h(k_2) \in h(K)\). The identity element \(e \in K\) maps to \(h(e) = e_{G_1}\) (the identity in \(G_1\)), so \(e_{G_1} \in h(K)\). If \(k \in K\), then \(k^{-1} \in K\) and hence \(h(k^{-1}) = h(k)^{-1} \in h(K)\). Thus, \(h(K)\) is a subgroup of \(h(G)\). To show \(h(K) \trianglelefteq h(G)\), we need to show that for every \(h(g) \in h(G)\) and \(h(k) \in h(K)\), \[ h(g) h(k) h(g)^{-1} \in h(K). \] Given \(h(g) \in h(G)\), there exists some \(g \in G\) such that \(h(g) = h(g)\). Similarly, for \(h(k) \in h(K)\), there exists some \(k \in K\). Consider the element \(gkg^{-1}\) in \(G\). Since \(K \trianglelefteq G\), we have: \[ gkg^{-1} \in K. \] Consider, \[ h(gkg^{-1}) = h(g)h(k)h(g^{-1}) = h(g)h(k)h(g)^{-1}. \] Since \(gkg^{-1} \in K\) and \(K\) is mapped into \(h(K)\), we get: \[ h(gkg^{-1}) \in h(K). \]

But \(h(gkg^{-1}) = h(g)h(k)h(g)^{-1}\), hence: \[ h(g)h(k)h(g)^{-1} \in h(K). \] This shows that \(h(K)\) is normal in \(h(G)\). Hence, \[ K \trianglelefteq G \implies h(K) \trianglelefteq h(G). \]

2. Discussed in Tutorial.

3.  Discussed in Tutorial.

Exercise \(\PageIndex{5}\)

 1. Let \(G\) be a group and let \(a \in G\) then show that \(\sigma_a :G \to G\) defined by \(\sigma_a(g)=aga^{-1}\)is an isormorphism.
2. Prove or disprove the following statements: 

a. \(U(5)\) is isormorphic to \( \mathbb{Z}_4\) .

b. \(\mathbb{Z}\) under addition is isormorphic to \(\mathbb{Q}\) under addition.

Answer

a. Let \(\phi: \; \mathbb{Z}_4 \rightarrow U(5)\) be defined by:  \(\phi(n)=2^n \pmod 5.\) That is 

\(\phi(0)=1\),  \(\phi(1)=2\),  \(\phi(3)=8 \equiv 3 \pmod{5}\), and \(\phi(2)=4\).

We will show \(\phi(a+b)=\phi(a)\phi(b), \; \forall a,b\in \mathbb{Z}_4\).

We will proceed by proof by exhaustion.  

There are 10 cases to consider since addition and multiplication are both commutative.

\(\phi(0+0)=\phi(0)=1=(1)(1)=\phi(0)\times \phi(0)\).

\(\phi(0+1)=\phi(1)=2=(1)(2)=\phi(0)\times \phi(1)\).

\(\phi(0+2)=\phi(2)=4=(1)(4)=\phi(0)\times \phi(2)\).

\(\phi(0+3)=\phi(3)=3=(1)(4)=\phi(0)\times \phi(3)\).

\(\phi(1+1)=\phi(2)=4=(2)(2)=\phi(1)\times \phi(1)\).

\(\phi(1+2)=\phi(3)=3=(1)(3)=\phi(1)\times \phi(3)\).

\(\phi(1+3)= \phi(0)=1\equiv (2)(3)=\phi(1)\times \phi(3)\).

\(\phi(2+2) = \phi(0)=1=(1)(1)=\phi(0)\times \phi(0)\).

\(\phi(2+3)= \phi(1)=2\equiv (4)(3)=\phi(2)\times \phi(3)\).

\(\phi(3+3)= \phi(2)=4 \equiv(3)(3)=\phi(3)\times \phi(3)\).

Having examined all the possible cases, \(\phi(ab)=\phi(a)\phi(b), \; \forall a,b\in \mathbb{Z}_4\).

b. Counterexample:

We know that \((\mathbb{Z},+)\) is a cyclic group generated by \(\langle -1\rangle\) and \(\langle +1 \rangle\).

Assume that \((\mathbb{Q}, +)\) is cyclic. We will show that \((\mathbb{Q}, +)\) is not cyclic.

Since \(\mathbb{Q}\) is cyclic, it can be generated by some \(\frac{p}{q}, p,q(\ne 0) \in \mathbb{Z}\). 

Thus \(\frac{p}{2q} = n \frac{p}{q}\) for some \(n \in \mathbb{Z}\). That is \(\frac{p}{2q} =  \frac{np}{q} \implies n=\frac{1}{2}.\)

This is a contradiction, and therefore \((\mathbb{Q}, +)\) is not cyclic.

 

 

Exercise \(\PageIndex{6}\)

 List or characterize all of the following rings' units. Justify your answer.

1.   \(\mathbb{Z}_{12}\)
2. \(M_{22}(\mathbb{Z}_2)\)
3. \(\mathbb{Z}(i)\)

Answer

1. Let \(a \in \mathbb{Z}_{12}\) be a unit. Then there exists \( x \in \mathbb{Z}_{12} \) such that \(ax \equiv 1\pmod{12}.\) Thus \( 12 \mid (ax-1) \implies (ax-1)=12y,\) for some \(y \in \mathbb{Z}.\) Therefore, \(ax-12y=1\). Hence \(gcd(a,12)=1.\) Therefore the units are \(1, 5, 7, 11.\)

2. Let \(A \in M_{22}(\mathbb{Z}_2)\) be a unit. . Then there exists \( X \in M_{22}(\mathbb{Z}_2)\) such that \begin{align*}AX= \begin{bmatrix}1 & 0 \\0 & 1\end{bmatrix}\end{align*}, and \(det(A) \ne 0.\) The determinant of a \( 2 \times 2 \) matrix \( A \) is:
\[
A = 
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix},
\quad \text{and} \quad
\det(A) = ad - bc \pmod{2}.
\]

We now list all matrices in \( M_2(\mathbb{Z}_2) \) with \( \det(A) \equiv 1 \pmod{2} \). These matrices are:
\[
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}, \quad
\begin{pmatrix}
1 & 1 \\
0 & 1
\end{pmatrix}, \quad
\begin{pmatrix}
1 & 0 \\
1 & 1
\end{pmatrix}, \quad
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}, \quad
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}, \quad
\begin{pmatrix}
0 & 1 \\
1 & 1
\end{pmatrix}.
\]

Thus, the units in \( M_2(\mathbb{Z}_2) \) are these six matrices. Each of these has an inverse in \( M_2(\mathbb{Z}_2) \), confirming that they are units.

 3. Let \(z = a + bi \in \mathbb{Z}[i]\) where \(a, b \in \mathbb{Z}\) be a unit. Then multiplicative inverse of \(z\) is given by $z^{-1}$. Then \( z  z^{-1} = 1 \implies |z || z^{-1}| = 1 \). Since \(|z|\) is a nonnegative integer, \(|z|=1.\) Thus \(a^2+b^2=1.) Hence \(a=\pm1\) or \(b=\pm 1\).

 Therefore the units of \(\mathbb{Z}[i]\) are \(\{-1, 1, -i, i\}\).

 

Exercise \(\PageIndex{7}\)

An element \(e\) of a ring \(R\) is said to be idempotent if \(e^2=e.\)

1.   If \(e\) is an idempotent of a ring \(R\), then show that \(1-2e\) is a unit.
2.  Find all idempotents in \(\mathbb{Z}_{12}\).
3.   Find all the idempotents in an integral domain \(R\).

Answer

1. Let \(e \in R\) be an idempotent of a ring\(R\). We shall show that \(1-2e\) is a unit of \(R. \)

Consider,\begin{eqnarray}(1-2e)(1-2e) &=& 1 - 2e - 2e + 4e^2 \nonumber \\&=& 1 - 4e + 4e \nonumber \\&=& 1. \nonumber\end{eqnarray}

Since \((1-2e)(1-2e) = 1\), \((1-2e)\) is a unit of \(R\).

2. Let \(x\) be an idempotent in \(\mathbb{Z}_{12}\), Then \(x^2 = 1 \pmod{12}\). Let's find these by exhaustion. 

\begin{align}\textbf{Idempotents} && \textbf{Non-Idempotents} \nonumber \\0^2 = 0 \equiv 0\pmod{12} && 2^2 = 4 \equiv 4\pmod{12}\nonumber \\1^2 = 1 \equiv 1\pmod{12} && 3^2 = 9 \equiv 9\pmod{12}\nonumber \\4^2 = 16 \equiv 4\pmod{12} && 5^2 = 25 \equiv 1\pmod{12} \nonumber \\9^2 = 81 \equiv 9\pmod{12} && 6^2 = 36 \equiv 0\pmod{12} \nonumber \\&& 7^2 = 49 \equiv 1\pmod{12} \nonumber \\&& 8^2 = 64 \equiv 4\pmod{12} \nonumber \\&& 10^2 = 100 \equiv 4\pmod{12} \nonumber \\&& 11^2 = 121 \equiv 1\pmod{12} \nonumber\end{align}

Therefore, the idempotents of \(\mathbb{Z}_{12}\) are \(\{0, 1, 4, 9\}.\)

3. Let \(e\) be an  idempotent in an integral domain \(R\). Then \(e^2 = e \implies e^2 - e = 0 \implies e(e-1) = 0.\)

Since the integral domain \(R\) contains no zero divisors,  \(e=0\) or \(e-1 = 0\). Therefore, the idempotents of \(R\) are \(0,\) and \(1\).