0E: Exercises

The real number system

Exercise \(\PageIndex{1}\)

Answer True or False for each of the statements below. If the statement is false, try to provide an example to demonstrate this.

1. The sum of any two integers is an integer.

2. The sum of any natural numbers is a natural number.

3. The difference between any two natural numbers is a natural number.

4. The sum of any two rational number is a rational number.

5. The sum of any two irrational number is an irrational number.

6. If the sum of the digits of an integer is divisible by \(3\), then the integer is divisible by \(3\).

7. If an integer has units digit \(0\) or \(5\) ( ends in either \(0\) or \(5\) ), then the integer is divisible by \(5\).

8. If \(n\) is an integer then

a. \(2n-1\) and \(2n+1\) are both odd integers.

b. \(2n\) is an even integer.

c. \(3n\) is an odd integer.

9. For any real number \(x\), \(|x| \leq 0.\)

10. For any real number \(x\), \(|x| \geq 0.\)

11. For any real number \(x\), and \(y\), \(|x| +|y|=|x+y|.\)

12. For any real number \(x\), and \(y\), \(|x| +|y| \geq |x+y|.\)

13. For any real number \(x\), it follows that \(\sqrt{x}\) is again real number.

a. \(\sqrt{x^2}=x.\)

b. \(\sqrt{x^2}=- x \mbox{ if } x<0.\)

Answer

1. True.

2. True.

3. False. \( 5-7=-2 \) is not a natural number.

4. True. (Note: The rational numbers include the integers.)

5. False. \( \sqrt{2} + -\sqrt{2} = 0 \).

6. True.

7. True.

8. a. True.

b. True.

c. False. \( 3 \times 2 = 6\) is even.

9. False. \( |3| = 3 > 0 \).

10. True.

11. False. \( |2| + |-2| = 2 + 2 = 4\) but \(|2 - 2| = 0 \).

12. False. Use same example as above.

Note: The correct statement is \( |x+y| \leq |x|+|y| \).

13. a. False. \( \sqrt{(-2)^2} = \sqrt{4} = 2 \neq -2 \).

b. True.

Exercise \(\PageIndex{2}\)

For each of the following terms, identify (a) its coefficient and (b) its degree in the variables which occur.

1. \(-2x^5\)

2. \(7x^3y\)

3. \(5\)

4. \(-4x^2y^3z^4\)

Answer

1. Coefficient: \( -2 \) ; degree \( 5 \).

2. Coefficient: \( 7 \); degree \( 4 \).

3. Coefficient: \( 5 \); degree \( 0 \).

4. Coefficient: \( -4\); degree \( 9 \).

Exercise \(\PageIndex{3}\)

Classify each of the expressions below as polynomial expression, rational expression or neither. If the expression is a polynomial, determine the coefficients of each of its terms.

1. \(2x^4-3x^3+7x^2-14x-19\)

2. \(3x^7-13x^3-x^{3/2}-21\)

3. \( \displaystyle \frac{1}{x^2}-5x+31\)

4. \(\displaystyle \frac{-2}{8x-1}\)

5. \( \displaystyle \frac{5x^2+3x-1}{7}\)

6. \(2x-\frac{1}{x}-1\)

7. \( \displaystyle \frac{3x+1}{3\sqrt{x}}\)

8. \(17\)

9. \(0\)

10. \( \displaystyle \frac{-4}{2x^2-x+1}\)

11. \( \displaystyle \frac{x^2-5x+1}{1-2x-3x^2}\)

12. \((x-3)(x+5)(2x-1)\)

13. \(\displaystyle \frac{\frac{1}{x}-3}{2-\frac{1}{x}}\)

14. \(\displaystyle \frac{\sqrt{(3x+1)}}{x^2-x-2}\)

15. \(\displaystyle \frac{1-x}{3+5x}\)

16. \(|x|\)

17. \(\left\{\begin{array}{cc}
\frac{2x-1}{x}, & x>0\\
&\\
x-1, & x \leq 0
\end{array}
\right.\)

18. \(\displaystyle \frac{3x+2}{\frac{1}{x}}\)

19. \( \displaystyle\frac{\frac{7x^2}{3 \sqrt{x}}}{x^{2/3}},\, x \ne 0.\)

20. \(x-2 \sqrt{x}-1\)

Answer

1. Polynomial; degree \( 4 \); coefficients \( 2 \), \( -3 \), \( 7 \), \( -14 \), \( 19 \).

2. Neither.

3. Neither.

4. Neither.

5. Polynomial; degree \( 2 \); coefficient \( \displaystyle \frac {5} {7} \), \( \displaystyle \frac {3} {7} \), \( \displaystyle \frac {-1} {7} \).

6. Neither.

7. Neither.

8. Polynomial; degree \( 0 \); coefficient \( 17 \).

9. Polynomial; degree \( 0 \); coefficient \( 0 \).

10. Rational Expression.

11. Rational Expression.

12. Neither.

13. Neither.

14. Neither.

15. Rational Expression.

16. Neither.

17. Neither.

18. Neither.

19. Neither.

20. Neither.

Exercise \(\PageIndex{4}\)

Identify each of the following numbers as natural numbers, integers, whole numbers, rational numbers, or irrational numbers.
\[\frac{-3}{4},\,-15,\,89,\,\frac{-4}{-23},\,-\sqrt{9},\,\sqrt{13},\,\frac{3}{10},\,-\sqrt{2}\]

Answer

\( \displaystyle \frac{-3}{4} \): rational number.

\( -15 \): integer, rational number.

\( 89 \): natural number, whole number, integer, rational number.

\( \displaystyle \frac{-4}{-23} \): rational number.

\( -\sqrt{9} = -3\): integer, rational number.

\( \sqrt{13} \): irrational number.

\( \displaystyle \frac{3}{10} \): rational number.

\( -\sqrt{2} \): irrational number.

Exercise \(\PageIndex{5}\)

A collection of real numbers is represented geometrically in each diagram below. In each case, give the interval representation.

1.

2.

3.

4.

5.

6.

7.

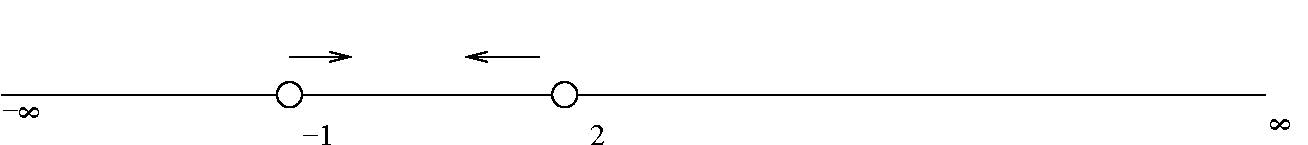
8.

9.

10.

11.

12.

13.

14.

15.

Answer

1. \( [4, \infty) \)

2. \( (-\infty, -7) \)

3. \( (-\infty, 1] \)

4. \( (-2, 7] \)

5. \( (-\infty, 8) \cup [15, \infty) \)

6. \( (-\infty, 7) \cup (7, \infty) \)

7. \( (-1, 2) \)

8. \( [-1, 2] \)

9. \( [-10,-3) \cup [1,5] \)

10. \( [1,2) \cup (2,3] \)

11. \( (-\infty,-1) \cup (-1,3) \cup [5, \infty) \)

12. \( {1, 3, 5} \)

13. \( (-\infty,-1) \cup (-1,2) \cup (2, \infty) \)

14. \( (-2,1] \cup (10,\infty) \)

15. \( [1,5) \cup (5,\infty) \)

Exercise \(\PageIndex{6}\)

Use long division (not calculators) to obtain a decimal representation of the following fractions.

1. \(\displaystyle \frac{3}{8}\)

2. \(\displaystyle \frac{2}{7}\)

3. \(\displaystyle \frac{2}{3}\)

4. \(\displaystyle \frac{1}{7}\)

5. \(\displaystyle \frac{2}{9}\)

6. \(\displaystyle \frac{3}{7}\)

7. \(\displaystyle \frac{3}{4}\)

8. \(\displaystyle \frac{4}{5}\)

9. \(\displaystyle \frac{4}{7}\)

10. \(\displaystyle \frac{5}{7}\)

11. \(\displaystyle \frac{6}{7}\)

12. \(\displaystyle \frac{5}{9}\)

13. \(\displaystyle \frac{8}{9}\)

14. \(\displaystyle \frac{7}{9}\)

Answer

1. \( \displaystyle \frac{3}{8} = 0.375 \)

2. \( \displaystyle \frac{2}{7} = 0.\overline{285714} \)

3. \( \displaystyle \frac{2}{3} = 0.\overline{6} \)

4. \( \displaystyle \frac{1}{7} = 0.\overline{142857} \)

5. \( \displaystyle \frac{2}{9} = 0.\overline{2} \)

6. \( \displaystyle \frac{3}{7} = 0.\overline{428571} \)

7. \( \displaystyle \frac{3}{4} = 0.75 \)

8. \( \displaystyle \frac{4}{5} = 0.2 \)

9. \( \displaystyle \frac{4}{7} = 0.\overline{571428}\)

10. \( \displaystyle \frac{5}{7} = 0.\overline{714285} \)

11. \( \displaystyle \frac{6}{7} = 0.\overline{857142} \)

12. \( \displaystyle \frac{5}{9} = 0.\overline{5} \)

13. \( \displaystyle \frac{8}{9} = 0.\overline{8} \)

14. \( \displaystyle \frac{7}{9} = 0.\overline{7} \)

Exercise \(\PageIndex{7}\)

Express each number given below as a product of its prime factors (in exponential form):

1. \(81\)

2. \(24\)

3. \(1080\)

Answer

1. \( 3^4 \)

2. \( 2^2 \cdot 3 \)

3. \( 2^3 \cdot 3^3 \cdot 5 \)

Exercise \(\PageIndex{8}\)

Evaluate each of the following using exponential laws:

1. \(2^6\)

2. \((-3)^5\)

3. \(\frac{1}{7^{-3}}\)

4. \(9^{-3}\)

5. \(\displaystyle \frac{2^5}{2^{-2}}\)

6. \(\displaystyle \frac{3^{-2}}{3^{-1}}\)

7. \(\left(\displaystyle \frac{-2}{-3}\right)^4\)

8. \(\left(\displaystyle \frac{2x}{5y}\right)^3\)

9. \((2^3)^2\)

10. \((5^{-2})^{-1}\)

11. \(\displaystyle \frac{5^{10}}{5^{7}}\)

12. \(\left(\displaystyle \frac{3}{4}\right)^{-2}\)

13. \(\left(\displaystyle \frac{51}{67}\right)^0\)

Answer

1. \( 2^6 = 64 \)

2. \( (-3)^5 = -243 \)

3. \( \displaystyle{\displaystyle \frac{1}{7^{-3}} = 7^3 = 343} \)

4. \( \displaystyle{9^{-3} = \displaystyle \frac{1}{9^3} = \displaystyle \frac{1}{729}} \)

5. \( \displaystyle{\displaystyle \frac{2^5}{2^{-2}} = 2^{5-(-2)} = 2^7 = 128} \)

6. \( \displaystyle{\displaystyle \frac{3^{-2}}{3^{-1}} = 3^{-2-(-1)} = 3^{-1} = \displaystyle \frac{1}{3} } \)

7. \( \displaystyle{\left (\displaystyle \frac{-2}{3} \right ) ^4 = \displaystyle \frac{(-2)^4}{3^4} = \displaystyle \frac{16}{81}} \)

8. \( \displaystyle{\left (\displaystyle \frac{2x}{5y} \right ) ^3 = \displaystyle \frac{(2x)^3}{(5y)^3} = \displaystyle \frac{8x^3}{125y^3}} \)

9. \( \displaystyle{\left (2^3 \right ) ^2 = 2 ^ {3 \cdot 2} = 2^6 = 64 } \)

10. \( \displaystyle{\left (5^{-2} \right ) ^{-1} = 5 ^ {(-2) \cdot (-1)} = 5^2 = 25 } \)

11. \( \displaystyle{\displaystyle \frac{5^{10}}{5^7} = 5^{10-7} = 5^3 = 125} \)

12. \( \displaystyle{\left (\displaystyle \frac{3}{4} \right ) ^{-2} = \displaystyle \frac{4^2}{3^2} = \displaystyle \frac{16}{9}} \)

13. \( \displaystyle{\left ( \displaystyle \frac{51}{67} \right ) ^{0} = 1} \)

Exercise \(\PageIndex{9}\)

Express each of the following in radical form:

1. \(x^{1/3}\)

2. \(\displaystyle \frac{1}{x^{1/2}}\)

3. \(x^{-2/5}\)

4. \(\displaystyle \frac{1}{x^{-3/4}}\)

5. \(x^{-1/9}\)

Answer

1. \( x^{1/3} = \sqrt[3] {x} \)

2. \( \displaystyle{\displaystyle \frac{1}{x^{1/2}} = \displaystyle \frac{1}{\sqrt{x}} = \displaystyle \frac{\sqrt{x}}{x}} \)

3. \( \displaystyle{x^{-2/5} = \displaystyle \frac{1}{x^{2/5}} = \displaystyle \frac{1}{\sqrt[5]{x^2}} = \displaystyle \frac{\sqrt[5]{x^3}}{x}} \)

4. \( \displaystyle{\displaystyle \frac{1}{x^{-3/4}} = x^{3/4} = \sqrt[4]{x^3}} \)

5. \( \displaystyle{x^{-1/9} = \displaystyle \frac{1}{x^{1/9}} = \displaystyle \frac{1}{\sqrt[9]{x}} = \displaystyle \frac{\sqrt[9]{x^8}}{x}} \)

Exercise \(\PageIndex{10}\)

Write the following radical expressions in exponent form:

1. \(\sqrt[4]{x}\)

2. \(\sqrt[3]{x^7}\)

3. \(\displaystyle \frac{1}{\sqrt[4]{x^3}}\)

4. \(\displaystyle \frac{\sqrt{x}}{\sqrt[3]{x}}\)

5. \(\displaystyle \frac{\sqrt[3]{x}\sqrt[5]{x}}{\sqrt{x}},\, x>0\)

6. \(\displaystyle \frac{1}{\sqrt[3]{x^{-2}}}\)

Answer

1. \( \sqrt[4]{x} = x^{1/4} \)

2. \( \sqrt[3]{x^7} = x^{7/3} \)

3. \( \displaystyle{\displaystyle \frac{1}{\sqrt[4]{x^3}} = x^{-3/4}} \)

4. \( \displaystyle{\displaystyle \frac{\sqrt x}{\sqrt[3]{x}} = x^{1/2 - 1/3} = x^{1/6}} \)

5. \( \displaystyle{\displaystyle \frac{\sqrt[3] {x} \sqrt[5] {x}}{\sqrt{x}} = x^{(1/3+1/5)-1/2} = x^{1/30}} \)

6. \( \displaystyle{\displaystyle \frac{1}{\sqrt[3]{x^{-2}}} = x^{2/3}} \)

Exercise \(\PageIndex{11}\)

Determine a real number value of each of the following if one exists. If one does not exist, explain why.

1. \(\sqrt[3]{-64}\)

2. \(\sqrt[3]{2^{15}}\)

3. \(\displaystyle \frac{1}{\sqrt{2^{6}}}\)

4. \(\sqrt{-400}\)

5. \(\sqrt[3]{(-2)^3}\)

6. \(\sqrt[4]{-16}\)

Answer

1. \( \sqrt[3]{-64} = -4 \)

2. \( \sqrt[3]{2^{15}} = 2 ^ {15/3} = 2^5 = 32 \)

3. \( \displaystyle{\displaystyle \frac{1}{\sqrt{2^6}} = \displaystyle \frac{1}{2^{6/2}} = \displaystyle \frac{1}{2^3} = \displaystyle \frac{1}{8} } \)

4. \( \sqrt{-400} \) is undefined because the square root of a negative number is undefined.

5. \( \sqrt[3] {(-2)^3} = -2 \)

6. \( \sqrt[4]{-16} \) is undefined because the fourth root of a negative number is undefined.

Exercise \(\PageIndex{12}\)

Simplify each of the following:

1. \(-3\sqrt{98}+5 \sqrt{12}-3\sqrt{24}+\sqrt{27}-2\sqrt{54}+4\sqrt{50}\)

2. \((2\sqrt{5}-3 \sqrt{2})(2\sqrt{5}+3 \sqrt{2})\)

3. \((2- \sqrt{3})(7+2\sqrt{3})\)

4. \((3\sqrt{5}-2 \sqrt{7})^2-(2\sqrt{5}+\sqrt{7})(\sqrt{5}-\sqrt{7})\)

5. \(\displaystyle \frac{\frac{5}{\sqrt{3}}}{\frac{-10}{3 \sqrt{3}}}\)

6. \(\displaystyle \frac{\sqrt{128}}{\sqrt{8}}\)

7. \( \sqrt{72}\,\sqrt{8}\)

Answer

1. \begin{eqnarray*}
-3\sqrt{98} + 5\sqrt{12} -3 \sqrt{24} + \sqrt{27} - 2\sqrt{54} + 4\sqrt{50} &=&
-21\sqrt{2} + 10\sqrt{3} -6 \sqrt{6} \\ & & + 3\sqrt{3} - 6\sqrt{6} + 20\sqrt{2} \\
&=& -\sqrt{2} + 13\sqrt{3} - 12\sqrt{6}
\end{eqnarray*}

2. \(
(2\sqrt{5} - 3\sqrt{2})(2\sqrt{5} + 3\sqrt{2}) =
(2\sqrt{5})^2 - (3 \sqrt{2})^2 = 4\cdot 5 - 9 \cdot 2 = 2
\)

3. \( (2 - \sqrt{3})(7 + 2\sqrt{3}) = 14 + 4\sqrt{3} - 7 \sqrt{3} - 2(3) = 8 - 3 \sqrt{3} \)

4. \begin{eqnarray*}(3\sqrt{5} - 2\sqrt{7})^2 - (2\sqrt{5} + \sqrt{7})(\sqrt{5} - \sqrt{7})
&=& 9\cdot 5 - 2(3\sqrt{5})(2\sqrt{7}) + 4 \cdot 7 \\
& &- 2\cdot 5 + 2 \sqrt{35} - \sqrt{35} + 7 \\
&=& 70-11\sqrt{35}
\end{eqnarray*}

5. \( \displaystyle \frac{\displaystyle \frac{5}{\sqrt{3}}}{\displaystyle \frac{-10}{3\sqrt{3}}} = \displaystyle \frac{5\cdot 3\sqrt{3}}{\sqrt{3}(-10)}
= -\displaystyle \frac{3}{2}\)

6. \(\displaystyle \frac{\sqrt{128}}{\sqrt{8}} = \displaystyle \frac{8\sqrt{2}}{2\sqrt{2}} = 4\)

7. \(\sqrt{72} \cdot \sqrt{8} = 3 \sqrt{8} \cdot \sqrt{8} = 3 \cdot 8 = 24 \)

Exercise \(\PageIndex{13}\)

Use order of operations to evaluate each of the following:

1. \(-31+35/7-(2)(24)+70\)

2. \(\displaystyle \frac{3^2-(-4)^2}{1-5^2}+\displaystyle \frac{7}{24}\)

Answer

1. \( -4 \)

2. \( \displaystyle \frac {7} {12} \)

Basic algebra

Exercise \(\PageIndex{1}\)

Simplify each of the following expressions:

1. \( 5x^3y^2-21xy+17x^3y^2-19xy+6\)

2. \(\frac{-3}{2}xz+\frac{5}{3}xz^2+\frac{7}{2}xz-\frac{19}{3}xz^2+4xz-19\)

3. \((3x^3y^2-7x^2y+5y^3-2)+(-5x^3y^2+4x^2y+11)\)

4. \(2x^2y^2\left((y^{-2}+24x^{-2}y-11x)-(2xy^{-2}-4x^{-2}y-11x+1)\right)\)

5. \(3xy(5x-7y)\)

6. \(3x^2y^4(2x^{-1}+9y^{-2}+4xy)\)

7. \((3x-2y)(4x^2-y^2)\)

8. \((x+y-2z)(x-y+2z)\)

9. \(\left( \displaystyle \frac{3}{x}-\displaystyle \frac{1}{y}\right)\left( \displaystyle \frac{5}{x}-\displaystyle \frac{2}{y}\right)\)

10. \(\displaystyle \frac{\displaystyle \frac{2}{x}-\displaystyle \frac{3}{y}}{\displaystyle \frac{-12}{x}+\displaystyle \frac{18}{y}}\)

Answer

1. \( 22x^3y^2 - 40 xy +6 \)

2. \( \displaystyle{6xz - \displaystyle \frac{14}{3} xz^2 - 19} \)

3. \( -2x^3y^2 -3x^2y + 5y^3 +9 \)

4. \( 2x^2+ 56y^3-4x^3 - 2x^2y^2 \)

5. \( 15x^2y - 21xy^2 \)

6. \( 6xy^4 + 27x^2y^2 + 12x^3y^5 \)

7. \( 12x^3-3xy^2-8x^2y + 2y^3 \)

8. \( x^2 - y^2 + 4yz - 4z^2 \)

9. \begin{eqnarray*}
\left ( \displaystyle \frac{3}{x} - \displaystyle \frac{1}{y} \right ) \left ( \displaystyle \frac{5}{x} - \displaystyle \frac{2}{y} \right )
& = & \left ( \displaystyle \frac{3y - x}{xy} \right ) \left ( \displaystyle \frac{5y +2x}{xy} \right ) \\
& = & \displaystyle \frac{(5y+2x)(3-x)}{(xy) ^2}
\end{eqnarray*}

10. \begin{eqnarray*}
\displaystyle \frac{\displaystyle \frac{2}{x} - \displaystyle \frac{3}{y}}{-\displaystyle \frac{12}{x} + \displaystyle \frac{18}{y}}
& = & \displaystyle \frac{\displaystyle \frac{2y - 3x}{xy}}{\displaystyle \frac{-12y + 18x}{xy}} \\
& = & \displaystyle \frac{(2y - 3x)(xy)}{(-12y + 18 x)(xy)} \\
& = & \displaystyle \frac{2y - 3x}{-6(2y-3x)} \\
& = & -\displaystyle \frac{1}{6}, 2y \neq 3x, xy \neq 0
\end{eqnarray*}

Factoring polynomials with some applications

Exercise \(\PageIndex{1}\)

Factor each of the expressions given. It may be necessary to apply the Factorization theorem.

1. \( 15x^3y^2-45xy^4\)

2. \( 12xz-4x^2z^2+36x\)

3. \( 2x^2-50\)

4. \( 7y^3-56\)

5. \( (3x-2)^2-(4y+3)^2\)

6. \( x^2-x-56\)

7. \( x^4-8x^2-9\)

8. \( x^4-10x^2+9\)

9. \( x^6+8y^6\)

10. \( z^2+64\)

11. \( 6x^2+19x+15\)

12. \( x^3+x^2-4x-4\)

13. \( yz-2ty+z^2-2tz\)

14. \( 2ac-4ad+3bc-6bd\)

15. \( 4x^3+500y^3\)

16. \( (x-2y)^2-2(x-2y)-8\)

17. \( 48-6t^3\)

18. \( x^8-256\)

19. \( y^2-4xy-45x^2\)

20. \( 2x^2-11x-21\)

21. \( 24x^2-98x-45\)

22. \( 24x^2-13x-45\)

23. \( x^6+19x^3-216\)

24. \( x^5-9x^3+8x^2-72\)

25. \( 3(x-2)^2(x+4)^5+5(x+4)^4(x-2)^3\)

26. \( x^4+x^2+1\)

27. \( x^4-12x^2+16\)

Answer

1. \( 15x^3y^2- 45xy^4 = 15xy^2(x^2-y^2) = 15xy^2(x-y)(x+y) \)

2. \( 12xz-4x^2z^2+36x = 4x(3z-xz^2 +9) \)

3. \( 2x^2-50 = 2(x^2- 25) = 2(x-5)(x+5) \)

4. \( 7y^3- 56 = 7(y^3 - 8) = 7 (y-2)(y^2+2y+4) \)

5. \begin{eqnarray*}
(3x-2)^2 - (4y+3)^2 &=& ((3x-2) - (4y+3))((3x-2)+(4y+3))
\\ &=& (3x -4y -5)(3x+4y +1)
\end{eqnarray*}

6. \( x^2-x-56 = (x-8)(x+7) \)

7. \( x^4 - 8x^2- 9 = (x^2 -9)(x^2+1) = (x-3)(x+3)(x^2+1) \)

8. \( x^4-10x^2+9 = (x^2-9)(x^2-1) = (x-3)(x+3)(x-1)(x+1) \)

9. \( x^6 + 8 y^6 = (x^2)^3 + (2y)^3 = (x^2 + 2y^2) (x^4 -2x^2y^2 + y^4) \)

10. \( z^2 + 64 \) does not factor.

11. \( 6x^2+19x+15 = (3x+5)(2x+3) \)

12. \begin{eqnarray*}
x^3+x^2-4x-4 &=& x^2(x+1) - 4(x+ 1) \\
&=& (x+1)(x^2-4)\\
&=& (x+1)(x-2)(x+2)
\end{eqnarray*}

13. \( yz-2ty+z^2-2tz = (y+z) (z-2t) \)

14. \( 2ac-4ad+3bc-6bd = (c-2d)(2a+3b) \)

15. \( 4x^3+ 500y^3 = 4(x+5y)(x^2-5xy+25y^2) \)

16. \( (x-2y)^2-2(x-2y)-8 = ((x-2y)-4)((x-2y)+2) \)

17. \( 48-6t^3 = 6(8-t^3) = 6(2-t)(4+2t+t^2) \)

18. \begin{eqnarray*}
x^8-256 &=& (x^4 - 16)(x^4+16) \\ &=& (x^2-4)(x^2+4)(x^4+16) \\ &=& (x-2)(x+2)(x^2+4)(x^4+16)
\end{eqnarray*}

19. \( y^2-4xy-45 x^2 = (y-9x)(y+5x) \)

20. \( 2x^2-11x-21 = (2x+3)(x-7) \)

21. \( 24x^2-98x-45 = (2x-9)(12x+5) \)

22. \( 24x^2-13x-45 = (3x-5)(8x+9) \)

23. \begin{eqnarray*}
x^6+ 19x^3-216 &=& (x^3 - 8) (x^3 + 27) \\ &=& (x - 2)(x^2+2x+4)(x+3)(x^2-3x+9)
\end{eqnarray*}

24. \begin{eqnarray*}
x^5-9x^3 + 8x^2-72 &=& x^3(x^2-9) + 8(x^2-9) \\ &=& (x^3+8)(x^2-9) \\ &=& (x-2)(x^2+2x+4)(x-3)(x+3)
\end{eqnarray*}

25. \begin{eqnarray*}
3(x-2)^2(x+4)^5 +5(x+4)^4(x-2)^3 &=& (x-2)^2(x+4)^4(3(x+4)+5(x-2)) \\ &=& 2(x-2)^2(x+4)^4(4x+1)
\end{eqnarray*}

26. \begin{eqnarray*}
x^4+x^2+1 &=& x^4 + 2x^2+1 -x^2 \\ &=& (x^2+1)^2 - x^2 \\ &=& (x^2+x+1)(x^2-x+1)
\end{eqnarray*}

27. \begin{eqnarray*}
x^4-12x^2+16 &=& x^4 -8x^2+16-4x^2 \\ &=& (x^2-4)^2 - 4x^2\\ &=& (x^2-2x-4)(x^2+2x-4)
\end{eqnarray*}

Exercise \(\PageIndex{2}\)

Evaluate each of the following:

1. \( \displaystyle{ \frac{2}{5}+\frac{4}{14}-\frac{7}{10}}\)

2. \( 6 \cdot \left(\displaystyle{ \frac{-2}{3}}\right)\)

3. \( \displaystyle{ \frac{17}{36}-\frac{1}{24}+\frac{5}{18}}\)

4. \( \displaystyle{ \frac{2}{19}\div \frac{5}{38}}\)

5. \( \displaystyle{ \frac{2}{9}-5+\frac{1}{2}}\)

6. \( \displaystyle{ \left(\frac{17}{52}\right)\,\left(\frac{26}{34}\right)}\)

7. \( \displaystyle{ \frac{\displaystyle\frac{-24}{7}}{\displaystyle\frac{-8}{49}}}\)

Answer

1. \( \displaystyle{\displaystyle \frac{-1}{70}} \)

2. \( -4 \)

3. \( \displaystyle{\displaystyle \frac{17}{24}} \)

4. \( \displaystyle{\displaystyle \frac{4}{5}} \)

5. \( \displaystyle{\displaystyle \frac{-77}{18}} \)

6. \( \displaystyle{\displaystyle \frac{1}{4}} \)

7. \( 21 \)

Exercise \(\PageIndex{3}\)

Simplify each of the expressions below:

1. \( \displaystyle{ \frac{x^2-4}{x^2-2x-8}-\frac{1}{x-4}}\)

2. \( \displaystyle{ \left(\frac{x^3-27}{x^2-6x+9}\right)\,\left(\frac{x^2-7x+6}{(x^2+3x+9)(x-6)}\right)}\)

3. \( \displaystyle{ \frac{2x^2-8}{2x^2+3x+1}-\frac{x^2-2x-35}{2x-6}\div\frac{2x^2-13x-7}{2x^2-4x-6}}\)

4. \( \displaystyle{ \frac{3}{(x-3)^2}-\frac{x}{x^2-9}}\)

5. \( \displaystyle{ \frac{\displaystyle{\frac{-1}{x}-\frac{3}{x-1}}}{\displaystyle\frac{2x-5}{x^2+3x-10}}}\)

6. \( \displaystyle{ \frac{\displaystyle{\frac{1}{x-1}+\frac{3}{(x+2)^2}-\frac{x}{x+3}}}{\displaystyle{\frac{4}{x-5}+\frac{2}{x+2}}}}\)

7. \( \displaystyle{ \frac{\displaystyle{\frac{2(x+h)-1}{3(x+h)+1}-\frac{2x-1}{3x+1}}}{h}}\)

Answer

1. \begin{eqnarray*}
\displaystyle \frac{x^2-4}{x^2-2x-8} - \displaystyle \frac{1}{x-4} &=& \displaystyle \frac{(x-2)(x+2)}{(x-4)(x+2)} -\displaystyle \frac{1}{x-4} \\
&=& \displaystyle \frac{x-2 + 1}{x-4} \\ &=& \displaystyle \frac{x-1}{x-4} \mbox{, $x \neq -2$}
\end{eqnarray*}

2. \begin{eqnarray*}
\displaystyle \frac{x^3-27}{x^2-6x+9} \cdot \displaystyle \frac{x^2-7x+6}{(x^2+3x+9)(x-6)}
&=& \displaystyle \frac{(x-3)(x^2+3x+9)(x-6)(x-1)}{(x-3)^2(x^2+3x+9)(x-6)} \\
&=&\displaystyle \frac{x-1}{x-3}, x \neq 6
\end{eqnarray*}

3. \begin{eqnarray*}
\displaystyle \frac{2x^2-8}{2x^2+3x+1} - \displaystyle \frac{x^2-x-35}{2x-6} \div \displaystyle \frac{2x^2-13x-7}{2x^2-4x-6}
&=& \displaystyle \frac{2x^2-8}{(2x+1)(x+1)} \\
& &-\displaystyle \frac{(x-7)(x+5)}{2(x-3)} \times \displaystyle \frac{2(x-3)(x+1)}{(2x+1)(x-7)}\\
&=& \displaystyle \frac{2x^2-8}{(2x+1)(x+1)} - \displaystyle \frac{(x+5)(x+1)}{2x+1} \\
&=& \displaystyle \frac{(2x^2-8) - (x+5)(x+1)^2}{(2x+1)(x+1)} \\
&=& \displaystyle \frac{2x^2-8 - (x^3+7x^2+11x-5)}{(2x+1)(x+1)} \\
&=& \displaystyle \frac{-x^3-5x^2-11x-3}{(2x+1)(x+1)}
\end{eqnarray*}

This cannot be reduced any further as \(2x+1\) and \(x+1\) are not factors of the numerator. We can use the remainder theorem to check:

Let \(p(x) = -x^3-5x^2-11x-3\). \(p(-1/2) = 19/8\) and \(p(-1) = 4\). Since neither of them are zero, then \(x = -1/2, -1\) are not zeros of \(p(x)\) and therefore \(2x+1\) and \(x+1\) are not factors of \(p(x)\).

4. \(\displaystyle \frac{3}{(x-3)^2} - \displaystyle \frac{x}{x^2-9} = \displaystyle \frac{3(x+3) - x(x-3)}{(x-3)^2(x+3)} = \displaystyle \frac{9+6x-x^2}{(x-3)^2(x+3)}\)

5. \begin{eqnarray*}
\displaystyle \frac{\displaystyle \frac{1}{x} - \displaystyle \frac{3}{x-1}}{\displaystyle \frac{2x-5}{x^2+3x-10}} &=& \displaystyle \frac{\displaystyle \frac{(x-1)-(3x)}{x(x-1)}}{\displaystyle \frac{2x-5}{(x+5)(x-2)}} \\
&=& \displaystyle \frac{-(2x+1)(x+5)(x-2)}{x(x-1)(2x-5)}
\end{eqnarray*}

6. \begin{eqnarray*}
\displaystyle \frac{\displaystyle \frac{1}{x-1} + \displaystyle \frac{3}{(x+2)^2} - \displaystyle \frac{x}{x+3} }{\displaystyle \frac{4}{x-5} + \displaystyle \frac{2}{x+2} }
&=& \displaystyle \frac{\displaystyle \frac{(x+2)^2(x+3) +3(x-1)(x+3) - x(x-1)(x+2)^2}{(x-1)(x+2)^2(x+3)}}{\displaystyle \frac{4(x+2)+2(x-5)}{(x-5)(x+2)}}\\
&=& \displaystyle \frac{-x^4-2x^3+10x^2+26x+3}{(x-1)(x+2)^2(x+3)} \cdot \displaystyle \frac{(x+2)(x-5)}{6x-2} \\
&=& \displaystyle \frac{(-x^4-2x^3+10x^2+26x+3)(x-5)}{(x-1)(x+2)(x+3)(6x-2)}, x \neq -2
\end{eqnarray*}

7. \begin{eqnarray*}
\displaystyle \frac{\displaystyle \frac{2(x+h)-1}{3(x+h)+1} - \displaystyle \frac{2x-1}{3x+1}}{h}
&=& \displaystyle \frac{1}{h} \left ( \displaystyle \frac{(2x+2h-1)(3x+1) - (2x-1)(3x+3h+1)}{(3x+3h+1)(3x+1)} \right )\\
&=& \displaystyle \frac{(6x^2+6xh-3x+2x+2h-1) - (6x^2+6xh+2x-3x-3h-1)}{h(3x+3h+1)(3x+1)} \\
&=& \displaystyle \frac{5h}{h(3x+3h+1)(3x+1)} \\
&=& \displaystyle \frac{5}{(3x+3h+1)(3x+1)}, h \neq 0
\end{eqnarray*}

Exercise \(\PageIndex{4}\)

Simplify each of the expressions below:

1. \( \displaystyle{ \frac{x^2-4}{x^2-2x-8}-\frac{1}{x-4}}\)

2. \( \displaystyle{ \left(\frac{x^3-27}{x^2-6x+9}\right)\,\left(\frac{x^2-7x+6}{(x^2+3x+9)(x-6)}\right)}\)

3. \( \displaystyle{ \frac{2x^2-8}{2x^2+3x+1}-\frac{x^2-2x-35}{2x-6}\div\frac{2x^2-13x-7}{2x^2-4x-6}}\)

4. \( \displaystyle{ \frac{3}{(x-3)^2}-\frac{x}{x^2-9}}\)

5. \( \displaystyle{ \frac{\displaystyle{\frac{-1}{x}-\frac{3}{x-1}}}{\displaystyle\frac{2x-5}{x^2+3x-10}}}\)

6.\(\displaystyle{\frac{\displaystyle{\frac{1}{x-1}+\frac{3}{(x+2)^2}-\frac{x}{x+3}}}{\displaystyle{\frac{4}{x-5}+\frac{2}{x+2}}}}\)

7. \( \displaystyle{ \frac{\displaystyle{\frac{2(x+h)-1}{3(x+h)+1}-\frac{2x-1}{3x+1}}}{h}}\)

Answer

Under construction.

Exercise \(\PageIndex{5}\)

Express your answer in its simplest form.

1. \( \displaystyle{ \frac{\sqrt{(2x+3)}-1}{x^2-x-2}}\)

2. \( \displaystyle{ \frac{\displaystyle \frac{1}{\sqrt{(x+1)}}-1}{x^2+2x}}\)

3. \( \displaystyle{ \frac{\sqrt{(2x^2+6x-7)}-1}{3x^2+2x-5}}\)

4. \( \displaystyle{ \frac{\sqrt{(3x+13)}-\sqrt{(17-x)}}{1-x^2}}\)

5. \( \displaystyle{ \frac{\displaystyle {\frac{1}{\sqrt{x}}-\frac{1}{\sqrt{2}}}}{x^2+2x-8}}\)

6. \( \displaystyle{ \frac{\displaystyle {\frac{1}{x+1}-\frac{1}{x}}}{\sqrt{(4x^2+3)}-2}}\)

7. \( \displaystyle{ \frac{\sqrt{(2x+2h+3)}-\sqrt{(2x+3)}}{h}}\)

8. \( \displaystyle{ \frac{\displaystyle {\frac{1}{\sqrt{(4-h)}}-\frac{1}{2}}}{h}}\)

Answer

1. \begin{eqnarray*}
\displaystyle \frac{\sqrt{2x+3} -1}{x^2-x-2}
&=& \displaystyle \frac{\sqrt{2x+3} -1}{(x-2)(x+1)} \cdot \displaystyle \frac{\sqrt{2x+3} +1}{\sqrt{2x+3} +1} \\
&=& \displaystyle \frac{(\sqrt{2x+3})^2-(1)^2}{(x-2)(x+1)(\sqrt{2x+3} +1)} \\
&=& \displaystyle \frac{2x+2}{(x-2)(x+1)(\sqrt{2x+3} +1)}\\
&=& \displaystyle \frac{2}{(x-2)(\sqrt{2x+3} +1)}
\end{eqnarray*}

2. \begin{eqnarray*}
\displaystyle \frac{\displaystyle \frac{1}{\sqrt{x+1}} -1}{x^2+2x}
&=& \displaystyle \frac{\sqrt{x+1} - (x+1)}{\sqrt{x+1}x(x+2)} \cdot \displaystyle \frac{\sqrt{x+1} +1)}{\sqrt{x+1} +1)}\\
&=& \displaystyle \frac{(\sqrt{x+1})^2 - (1)^2}{x(x+2)\sqrt{x+1}(\sqrt{x+1}+ 1))} \\
&=& \displaystyle \frac{x}{x(x+2)\sqrt{x+1}(\sqrt{x+1} +1)} \\
&=& \displaystyle \frac{-1}{(x+2)\sqrt{x+1}(\sqrt{x+1} +1)}, x \neq 0
\end{eqnarray*}

3. \begin{eqnarray*}
\displaystyle \frac{\sqrt{2x^2+6x-7} -1}{3x^2+2x-5}
&=& \displaystyle \frac{\sqrt{2x^2+6x-7} -1}{3x^2+2x-5} \cdot \displaystyle \frac{\sqrt{2x^2+6x-7} +1}{\sqrt{2x^2+6x-7} +1}\\
&=& \displaystyle \frac{2x^2+6x-7-1}{(3x+5)(x-1)(\sqrt{2x^2+6x-7} +1)}\\
&=& \displaystyle \frac{2(x+4)(x-1)}{(3x+5)(x-1)(\sqrt{2x^2+6x-7} +1)}\\
&=& \displaystyle \frac{2(x+4}{(3x+5)(\sqrt{2x^2+6x-7} +1)}, x \neq 1
\end{eqnarray*}

4. \begin{eqnarray*}
\displaystyle \frac{\sqrt{3x+13} - \sqrt{17-x}}{1-x^2}
&=& \displaystyle \frac{\sqrt{3x+13} - \sqrt{17-x}}{1-x^2} \cdot \displaystyle \frac{\sqrt{3x+13} + \sqrt{17-x}}{\sqrt{3x+13} + \sqrt{17-x}} \\
&=& \displaystyle \frac{(3x+13) - (17-x)}{(1-x)(1+x)(\sqrt{3x+13} + \sqrt{17-x})} \\
&=& \displaystyle \frac{4(x-1)}{(1-x)(1+x)(\sqrt{3x+13} + \sqrt{17-x})} \\
&=& -\displaystyle \frac{4}{(1+x)(\sqrt{3x+13} + \sqrt{17-x})}, x \neq 1
\end{eqnarray*}

5. \begin{eqnarray*}
\displaystyle \frac{\displaystyle \frac{1}{\sqrt{x}} - \displaystyle \frac{1}{\sqrt{2}}}{x^2+2x-8}
&=& \displaystyle \frac{\displaystyle \frac{\sqrt{x}}{x} - \displaystyle \frac{\sqrt{2}}{2}} {(x+4)(x-2)} \\
&=& \displaystyle \frac{2\sqrt{x} - \sqrt{2}x}{2x(x+4)(x-2)} \\
&=& \displaystyle \frac{2\sqrt{x} - \sqrt{2}x}{2x(x+4)(x-2)} \cdot \displaystyle \frac{2\sqrt{x} + \sqrt{2}x}{2\sqrt{x} + \sqrt{2}x}\\
&=& \displaystyle \frac{4x-2x^2}{2x(x+4)(x-2)(2\sqrt{x} + \sqrt{2}x)}\\
&=& -\displaystyle \frac{1}{(x+4)(2\sqrt{x} + \sqrt{2}x)}, x \neq 0, 2
\end{eqnarray*}

6. \begin{eqnarray*}
\displaystyle \frac{\displaystyle \frac{1}{x+1} + \displaystyle \frac{1}{x}}{\sqrt{4x^2+3}-2}
&=& \displaystyle \frac{2x+1}{x(x+1)(\sqrt{4x^2+3}-2)} \\
&=& \displaystyle \frac{2x+1}{x(x+1)(\sqrt{4x^2+3}-2)} \cdot \displaystyle \frac{\sqrt{4x^2+3}+2}{\sqrt{4x^2+3}+2}\\
&=& \displaystyle \frac{(2x+1)(\sqrt{4x^2+3}+2)}{x(x+1)(4x^2+3 -4)} \\
&=& \displaystyle \frac{(2x+1)(\sqrt{4x^2+3}+2)}{x(x+1)(2x-1)(2x+1)} \\
&=& \displaystyle \frac{\sqrt{4x^2+3}+2}{x(x+1)(2x-1)}, x \neq -1/2
\end{eqnarray*}

7. \begin{eqnarray*}
\displaystyle \frac{\sqrt{2x+2h+3}-\sqrt{2x+3}}{h}
&=& \displaystyle \frac{\sqrt{2x+2h+3}-\sqrt{2x+3}}{h} \cdot \displaystyle \frac{\sqrt{2x+2h+3}+\sqrt{2x+3}}{\sqrt{2x+2h+3}+\sqrt{2x+3}}\\
&=& \displaystyle \frac{(2x+2h+3)-(2x+3)}{h(\sqrt{2x+2h+3}+\sqrt{2x+3})} \\
&=& \displaystyle \frac{2h}{h(\sqrt{2x+2h+3}+\sqrt{2x+3})}\\
&=& \displaystyle \frac{2}{\sqrt{2x+2h+3}+\sqrt{2x+3}}, h \neq 0
\end{eqnarray*}

8. \begin{eqnarray*}
\displaystyle \frac{\displaystyle \frac{1}{\sqrt{4-h}} - \displaystyle \frac{1}{2}}{h}
&=& \displaystyle \frac{2 - \sqrt{4-h}}{2h\sqrt{4-h}} \\
&=& \displaystyle \frac{2 - \sqrt{4-h}}{2h\sqrt{4-h}} \cdot \displaystyle \frac{2 + \sqrt{4-h}}{2 + \sqrt{4-h}} \\
&=& \displaystyle \frac{4-(4-h)}{2h\sqrt{4-h}(2 + \sqrt{4-h})}\\
&=& \displaystyle \frac{1}{2\sqrt{4-h}(2 + \sqrt{4-h})}, h \neq 0
\end{eqnarray*}

Solving equations

Exercise \(\PageIndex{1}\)

Solve the following equations:

1. \(3x-17=0\)

2. \(-14z+21=0\)

3. \(\displaystyle \frac{-1}{2}x=\displaystyle \frac{7}{6}\)

4. \(3x-\displaystyle \frac{18}{7}=0\)

5. \(-5x=0\)

6. \(\displaystyle \frac{-2}{3}x=\displaystyle \frac{7}{5}\)

Answer

1. \( x = \displaystyle \frac {17} {3} \)

2. \( z = \displaystyle \frac {3} {2} \)

3. \( x = \displaystyle \frac {-7} {3} \)

4. \( x = \displaystyle \frac {6} {7} \)

5. \( x = 0 \)

6. \( x = \displaystyle \frac {-21} {10} \)

Exercise \(\PageIndex{2}\)

Solve each of the folwing quadratic equations by (a)factoring, (b)using the method of completing the square, (c) using the quadratic formula.

1. \(x^2-x-20=0\)

2. \(x^2-12x+36=0\)

3. \(4x^2+3x=0\)

4. \(10x^2+x-3=0\)

5. \(4x^2-4x+1=0\)

6. \(2x^2-5x-3=0\)

Answer

1. \( x = 5, -4 \)

2. \( x = 6 \)

3. \( x = 0, \displaystyle \frac {-3} {4} \)

4. \( x = \displaystyle \frac {1} {2} , \displaystyle \frac {-3} {5} \)

5. \( x = \displaystyle \frac {1} {2} \)

6. \( x = 3, \displaystyle \frac {-1} {2} \)

Exercise \(\PageIndex{3}\)

Use any method to solve the equations given below.

1. \(3t^2-14t=0\)

2. \(x^2+1=0\)

3. \(x^2+x+1=0\)

4. \(2x^2+x+5=0\)

5. \(36x^2-25=0\)

6. \(6x^2-31x+18=0\)

Answer

1. \( t= 0, 14/3 \)

2. There are no solutions: \(x^2 = -1\) only has complex solutions.

3. There are no solutions: Using the quadratic formula, we get \( \displaystyle{x = \displaystyle \frac{-1\pm\sqrt{-3}}{2}} \), which is a complex number.

4. There are no solutions: Using the quadratic formula, we get \( \displaystyle{x = \displaystyle \frac{-1\pm\sqrt{-39}}{4}} \), which is a complex number.

5. \( x = \pm \displaystyle \frac {5} {6} \)

6. \( x= \displaystyle \frac {9}{2}, \displaystyle \frac {2}{3} \)

Exercise \(\PageIndex{4}\)

Solve each of the following equations given for \(x.\)

1. \( \sqrt{(3x+1)}=2\)

2. \( \sqrt{(2x-3)}-\sqrt{(4x+1)}=-2\)

3. \( \displaystyle \sqrt{\frac{5x-2}{7x+4}}= \displaystyle \frac{2}{3}\)

4. \( \sqrt{(3x-5)}-4x+9=0\)

5. \( \sqrt{(2x-7)}=x-5\)

6. \( x^3-8=0\)

7. \(8 x^3+27=0\)

8. \( 6x^4-5x^2-6=0\)

9. \( x^{2/3}-5x^{1/3}-6=0\)

10. \( x- \sqrt{x}-12=0\)

11. \( 4x^{2/5}-4x^{1/5}+1=0\)

12. \( x^{3/2}-x^{3/4}-6=0\)

13. \(t^4-9t^2+8=0\)

14. \(y^4-2y^2-8=0\)

15. \(x^4-10x^2+9=0\)

16. \(x^6-26x^23-27=0\)

17. \(x-\sqrt{x}-2=0\)

18. \(x^3-17x^2+30x=0\)

19. \(t^{2/3}-t^{1/3}-6=0\)

20. \((x-1)(x+5)(2x+3)=0\)

21. \( \displaystyle \frac{x+10}{x+13}- \displaystyle \frac{2x}{3x-1}=0\)

22. \( \displaystyle \frac{2x^2+7x-15}{x^2+1}=0\)

23. \( \displaystyle \frac{x^2+1}{x^2+31}= \displaystyle \frac{1}{4}\)

24. \( \displaystyle \frac{2}{x-2}- \displaystyle \frac{9}{x+2}=0\)

25. \( \sqrt{(3x+15)}-x=5\)

26. \( \sqrt{(2x+14)}-5x=-1\)

27. \( \sqrt{(x+8)}+3=0\)

28. \( \sqrt{(x+4)}=\sqrt{(2x+1)}+1\)

29. \(|4x-3|=5\)

30. \(|x-1|=|7-x|\)

31. \(|2x+3|-3x+5=0\)

Answer

1.

2. \begin{eqnarray*}
\sqrt{2x-3} - \sqrt{4x+1} &=& -2 \\
\sqrt{2x-3} &=& \sqrt{4x+1} -2 \\
2x-3 &=& (4x+1) - 4\sqrt{4x+1} +4 \\
2x-3 &=& 4x + 5 - 4\sqrt{4x+1} \\
4\sqrt{4x+1} &=& 2x+8 \\
16(4x+1) &=& 4x^2 + 32x + 64 \\
x^2 - 8x +12 &=& 0 \\
x &=& 6, 2
\end{eqnarray*}

Check answers:
\(x = 6: \sqrt{9} - \sqrt{25} = -2 \,\surd\)
\(x = 2: \sqrt{1} - \sqrt{9} = -2 \,\surd\)

3. \begin{eqnarray*}
\sqrt{\displaystyle \frac{5x-2}{7x+4}} &=& \displaystyle \frac{2}{3} \\
\displaystyle \frac{5x-2}{7x+4} & =& \displaystyle \frac{4}{9} \\
9(5x-2) &=& 4(7x+4) \\
17x &=& 34 \\
x &=& 2
\end{eqnarray*}

Check answer:
\(\displaystyle{\sqrt{\displaystyle \frac{8}{18}} = \sqrt{\displaystyle \frac{4}{9}} = \displaystyle \frac{2}{3} \,\surd}\)

4. \begin{eqnarray*}
\sqrt{3x-5} -4x+9 &=&0 \\
\sqrt{3x-5} &=& 4x - 9 \\
3x-5 &= &16x^2 -72x + 81 \\
16x^2 -75x + 86 &=& 0 \\
(16x-43)(x-2) &=& 0 \\
x&=& 2, 43/16
\end{eqnarray*}

Check answer:
\(x=2: \sqrt{1} - 8+ 9 = 2 \rightarrow \) Not a solution
\(x = 43/16: \sqrt{49/16} - 43/4 +9 = -36/4+9 = 0 \,\surd\)

5. \begin{eqnarray*}
\sqrt{2x-7} &=& x-5 \\
2x-7 &=& x^2-10x+25 \\
x^2 -12x + 32 &=& \\
(x-8)(x-4) &=& 0 \\
x & =& 8, 4
\end{eqnarray*}

Check answers:
\(x = 8: \mbox{LHS} = \sqrt{9} = 3, \mbox{RHS} = 8-5 = 3 \,\surd \)
\(x = 4: \mbox{LHS} = \sqrt{1} = 1, \mbox{RHS} =4-5 = -1 \rightarrow\) Not a solution.

6. \(x^3-8 = (x-2)(x^2+2x+4) = 0\)
\(\displaystyle{x= 2}\).

7. \(8x^3 + 27 = (2x+3)(2x^2-6x+9) = 0\)
\(\displaystyle{x = - 3/2}\)

8. \(6x^4 - 5x^2 - 6 = (3x^2+2)(2x^2-3) = (3x^2+2)(\sqrt{2}x-\sqrt{3})(\sqrt{2}x+\sqrt{3}) = 0\)
\(\displaystyle{x = \pm\sqrt{\displaystyle \frac{3}{2}}}\)

9. Let \(u = x^{1/3}\)
\(u^2 - 5u - 6 = (u-6)(u+1) = 0\).
Therefore, \(x^{1/3} = u = -1, 6 \rightarrow x = -1, 216\).

10. Let \(u = \sqrt{x}\).
\(u^2- u -12 = (u-4)(u+3) = 0\).
Therefore, \(\sqrt{x} = u = 4, -3 \rightarrow x = 2\).

11. Let \(u = x^{1/5}\).
\(4u^2-4u +1 = (2u-1)^2 = 0\)
Therefore, \(x^{1/5} = u = 1/2 \rightarrow x = (1/2)^5 = 1/32\).

12. Let \(u= x^{3/4}\). Then \(u^2 = (x^{3/4})^2= x^{(3/4)*2} = x^{3/2}\).
\(u^2 -u - 6 = (u-3)(u+2) = 0\).
Therefore, \(x^{3/4} = u = 3, -2 \rightarrow x = 3^{4/3}\).
Note: \(x^{3/4} = -2\) is not a solution since \(x^{3/4} \geq 0\).

13. \(t^4-9t^2+8 = (t^2-8)(t^2-1) = (t-2\sqrt{2})(t+2\sqrt{2})(t-1)(t+1) = 0\)
\(t = \pm 2\sqrt{2}, \pm 1\)

14. \(y^4-2y^2-8 = (y^2-4)(y^2+2) = (y-2)(y+2)(y^2+2) = 0\)
\(y = \pm 2\)

15. \(x^4-10x^2+9 = (x^2-9)(x^2-1) = (x-3)(x+3)(x-1)(x+1) = 0\)
\(x = \pm 1, \pm 3\)

16. \(x^6-26x^3 -27 (x^3-27)(x^3+1) = (x-3)(x^2+3x+9)(x+1)(x^2+x+1)=0\)
\(x = 3, -1\)

17. Let \(u = \sqrt{x}\).
\(u^2-u - 2= (u-2)(u+1) = 0 \rightarrow \sqrt{x} = u = 2, -1 \rightarrow x = 4\)

18. \(x^3-17x^2+30x = x(x^2-17x+30) = x(x-15)(x-2) = 0 \rightarrow x= 0, 15, 2\)

19. Let \(u = t^{1/3}\).
\(u^2-u-6 = (u-3)(u+2) = 0 \rightarrow t^{1/3} = u = 3, -2 \rightarrow t = 27, -8\)

20. \(x = 1, -5, -3/2\)

21. Note: \(x \neq -13, 1/3\)
\begin{eqnarray*}
\displaystyle \frac{x+10}{x+13} - \displaystyle \frac{2x}{3x-1} &=& 0 \\
\displaystyle \frac{x+10}{x+13} &=& \displaystyle \frac{2x}{3x-1} \\
(x+10)(3x-1) &=& 2x(x+13) \\
3x^2+29x -10 &=& 2x^2 + 26x \\
x^2+3x-10 &=& 0 \\
(x+5)(x-2) &=& 0 \\
x &=& -5, 2
\end{eqnarray*}

22. \begin{eqnarray*}
\displaystyle \frac{2x^2+7x-15}{x^2 + 1} &=& 0 \\
2x^2+7x-15&=& 0 \\
(2x -3)(x+5) &=& 0 \\
x &=& 3/2, -5
\end{eqnarray*}

23. \begin{eqnarray*}
\displaystyle \frac{x^2+1}{x^2+31} &=& \displaystyle \frac{1}{4} \\
4(x^2+1) &=& x^2+31 \\
3x^2 -27 &=& 0 \\
3(x-3)(x+3) &=& 0 \\
x &=& \pm 3
\end{eqnarray*}

24. Note: \(x \neq 2, -2\)
\begin{eqnarray*}
\displaystyle \frac{2}{x-2} - \displaystyle \frac{9}{x+2} &=& 0 \\
\displaystyle \frac{2}{x-2} &=& \displaystyle \frac{9}{x+2} \\
2(x+2) &=& 9(x-2) \\
x &=& 22/7
\end{eqnarray*}

25. \begin{eqnarray*}
\sqrt{3x+15} -x &=& 5 \\
\sqrt{3x+15} &=& x+5 \\
3x+15 &=& x^2+10x+25 \\
x^2 + 7x +10 &=& 0\\
(x+5)(x+2) &=& 0 \\
x &=& -5, -2
\end{eqnarray*}

Check answers:
\(x=-5: \sqrt{0} + 5 = 5 \,\surd\)
\(x=-2: \sqrt{9} +2 = 3+2 = 5 \,\surd\)

26. \begin{eqnarray*}
\sqrt{2x+14} -5x &=& -1\\
\sqrt{2x+14} &=& 5x-1\\
2x+14 &=& 25x^2 - 10x +1 \\
25x^2 - 12x -13 &=& 0 \\
(25x + 13) (x-1) &=& 0 \\
x&=& -13/25, 1
\end{eqnarray*}

Check answers:
\(x= -13/25: \sqrt{324/25} + 13/5 = 18/25 + 13/5 = 31/5 \neq -1\).
Therefore, \(x= -13/25\) is not a solution.
\(x=1: \sqrt{16} - 5 = 4-5 = -1 \,\surd\).

27. \begin{eqnarray*}
\sqrt{x+8} +3 &=& 0 \\
\sqrt{x+8} &=& -3
\end{eqnarray*}

No solutions because \(\sqrt{x+8} > 0.\)

28. \begin{eqnarray*}
\sqrt{x+4} &=& \sqrt{2x+1} + 1 \\
x+4 &=& (2x+1) +2 \sqrt{2x+1} +1 \\
2\sqrt{2x+1} &=& 2-x \\
4(2x+1) &=& 4-4x + x^2 \\
x^2 -12x &=& 0 \\
x(x-12) &=& 0 \\
x &=& 0, 12
\end{eqnarray*}

Check answers:
\(x = 0: \mbox{LHS} = \sqrt{4} = 2; \mbox{RHS} = \sqrt{1} + 1 = 2 \,\surd\)
\(x = 12: \mbox{LHS} = \sqrt{16} = 4; \mbox{RHS} = \sqrt{25} + 1 = 6 \rightarrow \mbox{LHS} \neq
\mbox{RHS}, x= 12\) is not a solution.

29. Note: Use \(|a|^2 = a^2 = |a^2|\).

\begin{eqnarray*}
|4x-3| &=& 5 \\
(4x-3)^2 &=& 25 \\
16x^2-24x -16 &=& 0 \\
2x^2 - 3x - 2 &= & 0 \\
(2x+1)(x-2) &=& 0 \\
x&=& -1/2, 2
\end{eqnarray*}

30. \begin{eqnarray*}
|x-1| &=& |7-x| \\
x^2-2x+1 &=& 49 - 14x + x^2 \\
12x -48 &=& 0 \\
x &=& 4
\end{eqnarray*}

31. \begin{eqnarray*}
|2x+3| - 3x+5 &=& 0 \\
|2x+3| &=& 3x- 5 \mbox{ (Note: $3x-5 \geq 0 \rightarrow x \geq 5/3$)} \\
4x^2+ 12x+9 &=& 9x^2 -30x +25 \\
5x^2-42x+16 &=& 0 \\
(x-8)(5x-2) &=& 0 \\
x &=& 8, 2/5
\end{eqnarray*}

\(x = 2/5 < 5/3\). Therefore, it is not a solution. The solution set is \(x= 8\).

Exercise \(\PageIndex{5}\)

Solve each of the following systems of equations given below.

1. \begin{eqnarray*}
3x-4y&=-5\\
2x+5y&=12
\end{eqnarray*}

2. \begin{eqnarray*}
2x+y&=1\\
x+2y&=-4
\end{eqnarray*}

3. \begin{eqnarray*}
\displaystyle \frac{1}{2}x-\displaystyle \frac{2}{3}y&=1\\
-2x+y&=2
\end{eqnarray*}

4. \begin{eqnarray*}
x+\displaystyle \frac{3}{4}y&=\displaystyle \frac{1}{2}\\
4x-y&=1
\end{eqnarray*}

5. \begin{eqnarray*}
xy&=1\\
x^2+y^2&=4
\end{eqnarray*}
Leave your answer in radical form.

6. \begin{eqnarray*}
x^2-y^2&=9\\
x^2+y^2&=21
\end{eqnarray*}
Leave your answer in radical form

7. \begin{eqnarray*}
2x+y&=3\\
(x-3y)^2-(x-3y)-8&=0
\end{eqnarray*}

Answer

1. Solve for \(y\) (or \(x\), it doesn't matter) in one equation and substitute it
into the other equation. This creates an equation with one unknown. Solve for
the unknown.

If we solve for \(y\) in the first equation, we get =\(\displaystyle{y = \left ( \displaystyle \frac{1}{4} \right )(3x+5)}\). Substitute \(y\)
into the second equation \(\displaystyle{2x+ 5 \left ( \displaystyle \frac{1}{4} \right )(3x+5)) = 12}\). Simplify to \((23/4)x = 23/4\). Therefore,
\(x = 1\) and \(y = 1/4(3\cdot 1+5) = 8/4=2\).

2. Solve for \(y\) in equation 1 and substitute it into equation 2. Solve for \(x\).

\begin{eqnarray*}
y &=& 1-2x \\
x + 2(1-2x) &=& -4 \\
-3x +2 &=& -4 \\
x &=& 2 \\
y &=& -3
\end{eqnarray*}

3. Solve for \(y\) in equation 2 and substitute it into equation 1. Solve for \(x\).

\begin{eqnarray*}
y &=& 2 + 2x \\
\displaystyle \frac{1}{2}x - \displaystyle \frac{2}{3} \left (2+2x \right) &=& 1 \\
x &=& -\displaystyle \frac{14}{5} \\
y &=& -\displaystyle \frac{18}{5}
\end{eqnarray*}

4. Solve for \(x\) in equation 1 and substitute it into equation 2. Solve for \(y\).

\begin{eqnarray*}
x &=& \displaystyle \frac{1}{2} - \displaystyle \frac{3}{4}y \\
4 \left (\displaystyle \frac{1}{2} - \displaystyle \frac{3}{4}y \right ) -y &=& 1 \\
y &=& \displaystyle \frac{1}{4} \\
x &=& \displaystyle \frac{5}{16}
\end{eqnarray*}

5. Solve for \(y\) in equation 1 and substitute it into equation 2. Solve for \(x\).

\begin{eqnarray*}
y &=& \displaystyle \frac{1}{x} \\
x^2 + \left ( \displaystyle \frac{1}{x} \right ) ^2 &=& 4 \\
\displaystyle \frac{x^4+1}{x^2} &=& 4 \\
x^4+1 &=& 4x^2\\
x^4-4x^2+1 &=& 0 \\
x^2 &=& \displaystyle \frac{4 \pm \sqrt{12}}{2} \\
x^2 &=& 2 \pm \sqrt{3}
\end{eqnarray*}

Case 1: \(x^2 = 2 + \sqrt{3}\)
\(x = \pm \sqrt{2+ \sqrt{3}}, y = \pm \displaystyle \frac{1}{\sqrt{2+ \sqrt{3}}}\)
Case 2: \(x^2 = 2 - \sqrt{3}\)
\(x = \pm \sqrt{2-\sqrt{3}}, y = \pm \displaystyle \frac{1}{\pm \sqrt{2-\sqrt{3}}}\)

6. Equation 2 - Equation 1 yields \(2y^2 = 12.\)
Solve for \(y\): \(y = \pm \sqrt{6}.\)
Since \(x^2 = 21 - y^2 = 21 - 6 = 15\), \(x = \pm \sqrt{15}\).

7. Solve for \(y\) in the first equation: \(y = 3 - 2x\).
Substitute \(y\) into the second equation: \((x-3(3-2x))^2 - 2(x- 3(3-2x)) - 8 = (7x-9)^2 - 2(7x-9) - 8 = 0\).
Let \(u = 7x-9\): \(u^2 -2u-8 = (u-4)(u+2) = 0\).
Therefore, \(7x-9 = u = 4,-2\). \\
In conclusion, \(x = 1, y = 1\) or \(x = 13/7, y = -5/7\).

Inequalities

Exercise \(\PageIndex{1}\)

Answer true or false in each of the following statements. If the conclusion of the statement is not correct, make the correct conclusion.

1. \(a<b\) and \(c<b\) implies that \(a<c.\)

2. \(a<c\) and \(c<0\) implies that \(a<0.\)

3. \(a<b\) implies that \(\displaystyle \frac{1}{a}<\displaystyle \frac{1}{b}.\)

4. \(a<b\) implies that \(-a<-b\)

5. \(a<b\) implies that \(a^2<b^2\)

6. If \(a<b\) and both \(a\) and \(b\) are positive real numbers, then \(a^2<b^2\)

Answer

1. False. \(a<b\) and \(b<c\) implies that \(a<c\).

2. True.

3. False. \(a<b\) implies that \(\displaystyle{ \displaystyle \frac{1}{b} < \displaystyle \frac{1}{a} }\).

4. False. \(a<b\) implies that \(-a>-b\).

5. False. No correct conclusion.

6. True.

Exercise \(\PageIndex{2}\)

For each of the following, write without absolute value:

1. \(|-29|\)

2. \(|45|\)

3. \(|2x+5|^2\)

4. \((5x-1)^2-|1-5x|^2\)

5. \(\displaystyle \frac{|x|-x}{x} \mbox{ if } x<0\)

6. \(\displaystyle \frac{|x-2|-x+2}{x-2} \mbox{ if } x>2\)

Answer

1. \( 29 \)

2. \( 45 \)

3. \( |2y+5|^2 = (2y + 5)^2 = 4y^2 +20y +25 \)

4. \( (5x-1)^2 - |1-5x|^2 = (5x-1)^2 - (1-5x)^2 = 0 \)

5. \( \displaystyle{\displaystyle \frac{|x| - x}{x} = \displaystyle \frac{-x-x}{x} = -2, x \neq 0} \)

6. \( \displaystyle{\displaystyle \frac{|x-2| - x+2}{x-2} = \displaystyle \frac{x-2-x+2}{x-2} = 0} \)

Exercise \(\PageIndex{3}\)

Solve each of the following inequalities:

1. \(x^2-3x \leq 4\)

2. \(2x^2-5x+2 >0\)

3. \(4-3x \geq 0\)

4. \(4x^2-28x +49\leq 0\)

5. \((x-3)(x^2+1) <0\)

6. \(x^2+24 <0\)

7. \(\displaystyle \frac{x^2-x-20}{x^3(x+1)} \leq 0\)

8. \(\displaystyle \frac{2x^2-x-1}{x^2-16} < 0\)

9. \(\displaystyle \frac{x^2+1}{(x-1)^2(2-x)} < 0\)

10. \(\displaystyle \frac{(2x-1)^2(x^2+1)(3x-2)}{(x-2)(x^2-x+4)} \leq 0\)

11. \(|2x+5| >2\)

12. \(|1-x| \leq |x+1|\)

13. \(|2x-1| \leq|5x-1|\)

14. \(\displaystyle \frac {|2+x|}{|2-x|} >1\)

15. \(|4x-1| <x\)

16. \(|2x-3| \geq x\)

Answer

1. Isolate all of the terms on one side of the inequality: \(x^2-3x-4 \leq 0\).

Factor: \((x-4)(x+1) \leq 0\).

Make a sign chart:

Solution: \(x \in [-1,4]\).

2. Factor: \((2x-1)(x-2)\).

Make a sign chart:

Solution: \(x \in (-\infty,1/2) \cup (2, \infty)\).

3. Since \(4-3x\) is linear, solve for \(x\): \(x \leq 4/3\)

4. Factor: \((4x-7)^2\).

Anything squared is always positive. Therefore, \(4x^2-28x+49\) is never negative but it is zero.

Solution: \(x = 7/4\)

5. Make a sign chart:

Solution: \(x \in (-\infty,3) \).

6. \(x^2+24\) is always positive. Therefore, there is no solution.

7. Note: \(x \neq 0, -1\)

Factor: \(\displaystyle{\displaystyle \frac{(x-5)(x+4)}{x^3(x+1)}}\).

Make a sign chart:

Solution: \(x \in [-4, -1) \cup (0,5] \).

8. Note: \(x \neq \pm 4\)

Factor: \(\displaystyle{\displaystyle \frac{(2x+1)(x-1)}{(x-4)(x+4)}}\).

Make a sign chart:

Solution: \(x \in (-4, -1/2) \cup (1,4) \).

9. Note: \(x \neq 1,2\)

Make a sign chart:

Solution: \(x \in (2, \infty)\).

10. Note: \(x \neq 2\) and \(x^2-x+4\) is not factorable.

Make a sign chart:

Solution: \(x \in [2/3, 2) \).

11. Case 1: If \(2x+5 \geq 0\), then \(|2x+5| = 2x + 5\)

\(2x+5 >2 \rightarrow x > -3/2\)

Case 2: If \(2x + 5 < 0\), then \(|2x+5| = -(2x+5)\)

\(-2x-5 > 2 \rightarrow x < -7/2\)

Solution: \(x \in (-\infty, -7/2) \cup (-3/2, \infty)\)

12. \begin{eqnarray*}
|1-x| &\leq & |x+1| \\
1-2x+x^2 &\leq & x^2 + 2x + 1 \\
0&\leq & 4x \\
0 &\leq & x
\end{eqnarray*}

13. \begin{eqnarray*}
|2x-1| & \leq & |5x-1| \\
4x^2-4x+1 & \leq& 25x^2 -10x + 1 \\
0 & \leq & 16x^2 +6x = 2x(8x+3)
\end{eqnarray*}

Make a sign chart to get the solution \(x \in (-\infty, -3/8] \cup [0, \infty)\).

14. Note: \(x \neq 2\) and \((2-x)^2>0\), therefore we can multiply both sides of the inequality by it.

\begin{eqnarray*}
\left | \displaystyle \frac{2+x}{2-x} \right | & >& 1 \mbox{ Square both sides} \\
\displaystyle \frac{4+4x+x^2}{4 - 4x + x^2} &>& 1 \mbox{ Since $(2-x)^2$ is positive we can cross multiply}\\
4+4x+x^2 &>& 4-4x+x^2 \\
8x & > & 0
\end{eqnarray*}

Solution: \(x >0\)

15. Note: \(x \geq 0\)

\begin{eqnarray*}
0 \leq |4x-1| &<& x \\
16x^2 -8x + 1 & < & x^2\\
15x^2-8x+1 &<& 0 \\
(3x-1)(5x-1) &<& 0
\end{eqnarray*}

Make a sign chart to get the solution \(x \in (1/5, 1/3)\).

16. \begin{eqnarray*}
|2x-3| &\geq& x \\
4x^2 -12x + 9 & \geq & x^2\\
3x^2-12x+9 &\geq& 0 \\
3(x-1)(x-3) &\geq& 0
\end{eqnarray*}

Make a sign chart to get the solution \(x \in (-\infty, 1) \cup (3, \infty)\).

Analytic geometry

Exercise \(\PageIndex{1}\)

In each cases, Given points \(P\) and \(Q,\) determine

a)the slope of the line segment \(PQ\),

b) the midpoint, \(M\), of the line segment \(PQ\) and

c) the lengh of the line segment \(PQ\).

1. \(P=(-2,9),\, Q=(2,6)\)

2. \(P=(0,0),\, Q=(-6,8)\)

3. \(P=(5,-3),\, Q=(7,-3)\)

4. \(P=(7,-2),\, Q=(7,-9)\)

5. \(P=(11,0),\, Q=(0,-60)\)

6. \(P=(6,-5),\, Q=(-6,0)\)

7. \(P=(13,-2),\, Q=(5,13)\)

Answer

1. a) \(\displaystyle{-\displaystyle \frac{3}{4}}\), b) \(\displaystyle{\left ( 0, \displaystyle \frac{15}{2} \right )}\), c) \(5\)

2. a) \(\displaystyle{-\displaystyle \frac{4}{3}}\), b) \(\displaystyle{(-3, 4)}\), c) \(10\)

3. a) \(0\), b) \(( 6, -3)\), c) \(2\)

4. a) undefined, b) \(\displaystyle{\left ( 7, -\displaystyle \frac{11}{2} \right )}\), c) \(7\)

5. a) \(\displaystyle{\displaystyle \frac{60}{11}}\), b) \(\displaystyle{\left ( \displaystyle \frac{11}{2}, -30 \right )}\), c) \(61\)

6. a) \(\displaystyle{-\displaystyle \frac{5}{12}}\), b) \(\displaystyle{\left ( 0, -\displaystyle \frac{5}{2} \right )}\), c) \(13\)

7. a) \(\displaystyle{-\displaystyle \frac{15}{8}}\), b) \(\displaystyle{\left (9, \displaystyle \frac{11}{2} \right )}\), c) \(17\)

Exercise \(\PageIndex{2}\)

1. Find the equation of the straight line passing through \((1,-2)\) and which has a slope of \(-2\).

2. Find the equation of the straight line passing through \((2,-3)\) that is

a) parallel to the line \(2x-5y+3=0\).

b) perpendicular to the line \(2x-5y+3=0.\)

Answer

1. \(y = -2x\)

2. a) \(\displaystyle{y = \displaystyle \frac{2}{5}x - \displaystyle \frac{19}{5}}\)

b) \(\displaystyle{y = -\displaystyle \frac{5}{2}x +2}\)

Exercise \(\PageIndex{3}\)

1. Find the equation of the straight line passing through the midpoint of the line segment \(PQ\) and perpendicular to \(PQ\) given that \(P=(-1,3),\) and \(Q=(5,-7).\)

2. Find the equation of the straight line which contains both of the points \(A=(4,-2),\) and \(B=(7,-2).\)

3. Find the equation of the straight line which contains the point \((-1,5)\) and is parallel to the \(x-\)axis.

4. Find the equation of the straight line which contains the point \((10,-1)\) and is parallel to the \(y-\)axis.

Answer

1. \(\displaystyle{y = \displaystyle \frac{3}{5}x - \displaystyle \frac{16}{5}}\)

2. \(y = -2\)

3. \(y= 5\)

4. \(x = 10\)

Exercise \(\PageIndex{4}\)

Which of the following pairs of lines is parallel?, perpendicular?, neither parallel nor perpendicular?

1. \begin{eqnarray*}
4x+3y-2 &= 0\\
2x &= 7y-1
\end{eqnarray*}

2. \begin{eqnarray*}
\displaystyle \frac{1}{2}x- \displaystyle \frac{3}{4}y+1&=0\\
9y-6x+3&=0
\end{eqnarray*}

3. \begin{eqnarray*}
x+11&=0\\
2y-7&=0
\end{eqnarray*}

4. \begin{eqnarray*}
3x+7y+1&=0\\
35x-15y-2&=0
\end{eqnarray*}

Answer

1. Neither parallel nor perpendicular.

2. Parallel.

3. Perpendicular.

4. Perpendicular.

Exercise \(\PageIndex{5}\)

Sketch the graph of each of the following straight lines:

1. \(3x-6y-2=0\)

2. \(7x+5y-35=0\)

3. \(2x-y=0\)

4. \(3x+4y=0\)

5. \(2y-11=0\)

6. \(3x+2=0\)

Answer

1.

2.

3.

4.

5.

6.

Exercise \(\PageIndex{6}\)

Determine the point of intersection of each of the following pairs of lines, if they exists.

1. \(2x+5y=-11 \mbox{ and } 7x-4y=26 \)

2. \(2x+-3y=1 \mbox{ and } \displaystyle \frac{1}{2}x-\displaystyle \frac{3}{4}y=\displaystyle \frac{-1}{4}\)

Answer

1. \(x=2, y = -3\)

2. The lines are parallel. Therefore, there is no point of intersection.

Exercise \(\PageIndex{7}\)

1. Given that \(A=(3,4),\, B=(-2,3),\) and \(C=(2,-1),\) show that the triangle \(ABC\) is isoceles. (An isoceles triangle is a triangle in which two of the sides have the same length.)

2. Given that \(A=(5,3),\, B=(-2,2),\) and \(C=(2,-1),\) show that the triangle \(ABC\) has a right angle at \(C.\) (Hint: Recall Theorem of Pythagoras'.)

3. Show that the points \(P=(1,-1),\, Q=(0,2)\) and \(R=(-1,5)\) are collinear (lie on the same line).

4. Use the distance formula to show that the triangle \(ABC\) is an equilateral triangle, given that \(A=(1,0),\, B=(5,0),\) and \(C=(3,2/3).\) (An equilateral triangle is triangle in which all sides are of equal length).

5. If \(ABCD\) is parallelogram with \(A=(7,-3),\,B=(8,3),\) and \(C=(3,5),\) determine the coordinates of the vertex \(D.\)

Answer

1. \(\overline{AB} = (-5, -1)\) and \(|\overline{AB}| = \sqrt{(-5)^2 + (-1)^2} = \sqrt{26}\)
\(\overline{AC} = (-1, -5)\) and \(|\overline{AC}| = \sqrt{(-1)^2 + (-5)^2} = \sqrt{26}\)

Since two of the lines of the triangle have equal length, the three points form an isoceles triangle.

2. \(\overline{AB} = (-7,-1)\) and \(|\overline{AB}| = \sqrt{(-7)^2 + (-1)^2} = 5\sqrt{2}\)
\(\overline{AC} = (-3,-4)\) and \(|\overline{AC}| = \sqrt{(-3)^2 + (-4)^2} = 5\)
\(\overline{BC} = (4,-3)\) and \(|\overline{BC}| = \sqrt{(4)^2 + (-3)^2} = 5\)

Pythagoras' theorem is only true for right angled triangles:

\(|\overline{AC}|^2 + |\overline{BC}|^2 = (5)^2 + (5)^2 = 50\). If the triangle is right angled, we would expect that \(\sqrt{50} = 5\sqrt{2}\) would equal \(|\overline{AB}|\). It does!

3. Find the equation of the line containing the points \(P\) and \(Q\).

Slope = =\(-3\).

Line: \(y = -3x +2\).

Check if \(R\) lies on the line: If \(x = -1\), \(y = -3(-1) + 2 = 5\).
Therefore, the point \(R = (-1,5)\) is on the line and the three points are collinear.

4. \(\overline{AB} = (4, 0)\) and \(|\overline{AB}| = \sqrt{(4)^2} = 4\)
\(\overline{AC} = (2, 2\sqrt{3}\) and \(|\overline{AB}| = \sqrt{(2)^2 + (2\sqrt{3})^2} = 4\)
\(\overline{BC} = (2, 2\sqrt{3})\) and \(|\overline{AB}| = \sqrt{(-2)^2 + (2\sqrt{3})^2} = 4\)

Since \(|\overline{AB}| = |\overline{AC}| = |\overline{BC}|\), it is an equilateral triangle.

5. Let \(D= (h,k)\) so that \(ABCD\) is a parallelogram.

\begin{eqnarray*}
m_{\overline{AD}} = m_{\overline{BC}} \Rightarrow \displaystyle \frac{k+3}{h-7} &=& \displaystyle \frac{5-3}{3-8} \\
-5(k+3) &=& 2(h-7) \\
2h + 5k &=& -1 \hspace{5mm} (1)
\end{eqnarray*}

\begin{eqnarray*}
m_{\overline{AB}} = m_{\overline{CD}} \Rightarrow \displaystyle \frac{k-5}{h-3} &=& \displaystyle \frac{6}{8-7} \\
k-5 &=& 6(h-3) \\
6h -k &=& 13 \hspace{5mm} (2)
\end{eqnarray*}

To determine \(h\) and \(k\) solve (1) and (2) simultaneously to obtain \(h = 2\) and \(k = -1\).
Thus, \(D = (2, -1)\).

Exercise \(\PageIndex{8}\)

Find an equation of the circle with center and radius as indicated:

1. Center \((4,3)\), radius \(=9.\)

2. Center \((-1,2)\), radius \(=\sqrt{5}.\)

3. Center \((2,0)\), radius \(=1.\)

4. Center \((0,0)\), radius \(=1.\)

5. Center \((-7,-3)\), radius \(=\displaystyle \frac{\sqrt{17}}{2}.\)

6. Center \((0,-4)\), radius \(=3.\)

Answer

1. \((x-4)^2 + (y - 3)^2 = 81\)

2. \((x+1)^2 + (y - 2)^2 = 5\)

3. \((x-2)^2 + y^2 = 1\)

4. \(x^2 + y^2 = 1\)

5. \((x+7)^2 + (y + 3)^2 = 17/4\)

6. \(x^2+(y+4)^2 = 9\)

Exercise \(\PageIndex{9}\)

Find the center and radius of the following circles:

1. \((x-1)^2+(y+3)^2=16\)

2. \((x+2)^2+(y+1)^2=24\)

3. \(x^2+y^2=3\)

4. \((x-7)^2+y^2=64\)

5. \(x^2+(y+2)^2=1\)

6. \(x^2+y^2-2x+2y+1=0\)

7. \(x^2+y^2+8x-6y+17=0\)

8. \(x^2+y^2-4y+1=0\)

9. \(4x^2+4y^2-4x+16y+13=0\)

10. \(9x^2+9y^2+18x+8=0\)

Answer

1. Centre at \((1, -3)\), radius = \(4\).

2. Centre at \((-2, -1)\), radius = \(2\sqrt{6}\).

3. Centre at \((0, 0)\), radius = \(\sqrt{3}\).

4. Centre at \((7, 0)\), radius = \(8\).

5. Centre at \((0, -2)\), radius = \(1\).

6. Complete the square to find the centre and radius.
\((x-1)^2+ (y+1)^2 = 1\)
Centre at \((1, -1)\), radius = \(1\).

7. \((x+4)^2+ (y-3)^2 = 8\)
Centre at \((-4, 3)\), radius = \(2\sqrt{2}\).

8. \(x^2+ (y-2)^2 = 3\)
Centre at \((0, 2)\), radius = \(\sqrt{3}\).

9. \((x-1/2)^2+ (y+2)^2 = 1\)
Centre at \((1/2, -2)\), radius = \(1\).

10. \((x+1)^2+ y^2 = 1/9\)
Centre at \((-1,0)\), radius = \(\displaystyle \frac {1}{3} \).

Exercise \(\PageIndex{10}\)

1. Find an equation of the circle centered at \((1,5)\) passing through the point \((7,-1).\)

2. Determine the equation of the circle with diameter \(PQ,\) where \(P=(-1,1)\) and \(Q=(2,0).\)

3. Determine the equation of the circle with center \(C=(-3,5)\) and tangent to

a) the \(x-\)axis

b) the \(y-\)axis

4. Determine the equation of the circle with center \(C=(3,-5)\) and tangent to

a) the \(x-\)axis

b) the \(y-\)axis

Answer

1. We know that the equation will be \((x+1)^2 + (y-5)^2 = r^2\), where \(r\) is the radius.
Substitute \((7, -1)\) into the equation and solve for \(r\).
\[8^2 + (-6)^2 = 64+36 =100 = r^2 \rightarrow r = 10\]
Therefore, the equation of the circle is \((x+1)^2 + (y - 5)^2 = 100\).

2. The radius is half the distance between the two points: \(\sqrt{10}/2\).
The centre will be the midpoint between the two points: \(\displaystyle{\left ( \displaystyle \frac{1}{2},-\displaystyle \frac{1}{2} \right ) }\).
\[(x-1/2)^2 +(y + 1/2)^2 = 5/2\]

3. a) \((x+3)^2+ (y -5)^2 = 25\)

b) \((x+3)^2+ (y -5)^2 = 9\)

4. a) \((x-3)^2+ (y +5)^2 = 25\)

b) \((x-3)^2+ (y +5)^2 = 9\)

Exercise \(\PageIndex{11}\)

1. Find an equation of the circle with center at \((2,-3)\) and radius of length \(4\) units.

2. Find an equation of the circle which has center at the point \((4,-7)\) and which contains the point \((2,1).\)

3. Find an equation of the circle which has diameter \(AB\), where \(A=(2,3)\) and \(B=(6,-1).\)

4. Find an equation of the circle which is tangent to the \(x-\)axis at the point \((-2,0),\) and is tangent to the \(y-\)axis at the point \((0,2).\)

Answer

1. \((x-2)^2 + (y +3)^2 = 4\)

2. \((x-4)^2 + (y +7)^2 = 68\)

3. \((x-4)^2 + (y -1)^2 = 32\)

4. \((x+2)^2 + (y -2)^2 = 4\)

Exercise \(\PageIndex{12}\)

Classify each equation given as being an equation of a parabola, an ellipse, a circle, a hyperbola or none of these.

1. \( 4x^2-y^2+8x+4y+3=0\)

2. \( 4x^2+5y^2-8x+15y=1\)

3. \( x^2+y^2+12x-8y=0\)

4. \( 4x^2+y-3=0\)

5. \( 4x+y^2-2y+4=0\)

6. \( 4x^2+y^2+3y-4=0\)

7. \( 2x^2-3y^2-6x+12y=1\)

8. \( 3x+2y-5=0\)

9. \( x^2+5y^3-3x+2y-1=0\)

10. \( x^3+y^3=1\)

11. \( (x-1)^2+(y+3)^2=22\)

12. \( (x-1)^2-(y+3)^2=22\)

Answer

The general form of a conic is \(Ax^2 + By^2 + Cxy + Dx + Ey + F = 0\).
If the conic is not degenerate, then we can use the general form to classify the conic.
If \(A = B\), then the conic is a circle.
If \(A \neq B\), then the conic is an ellipse if \(A\) and \(B\) are both positive, the conic is a hyperbola if \(A\) and \(B\) are opposite signs, and the conic is a parabola if \(A\) or \(B\) is zero.

1. Hyperbola.

2. Ellipse.

3. Circle.

4. Parabola.

5. Parabola.

6. Parabola.

7. Hyperbola.

8. Degenerate conic.

9. Not a conic.

10. Not a conic.

11. Circle.

12. Hyperbola.

Trignometry

Exercise \(\PageIndex{1}\)

1. In each of the triangle, determine the values of \( \sin (\alpha), \cos(\alpha), \tan (\alpha), \sec (\alpha),
\csc (\alpha), \) and \(\cot (\alpha).\)

a)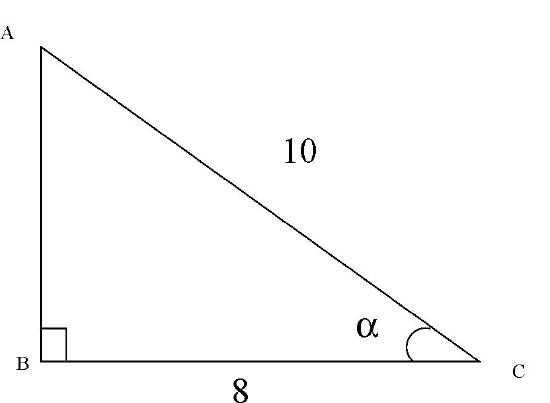

b)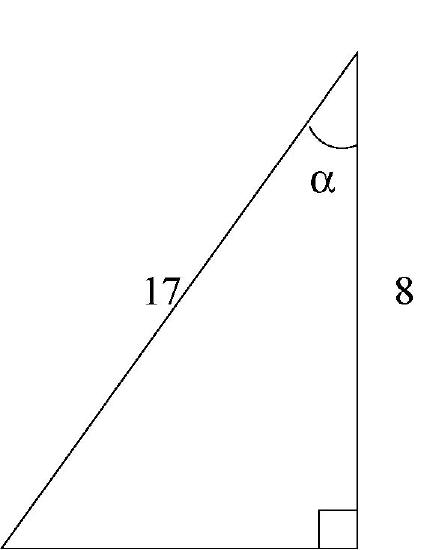

2. Use the information provided in the diagram to determine \(\cot (t), \sin (t), \sec (t).\)

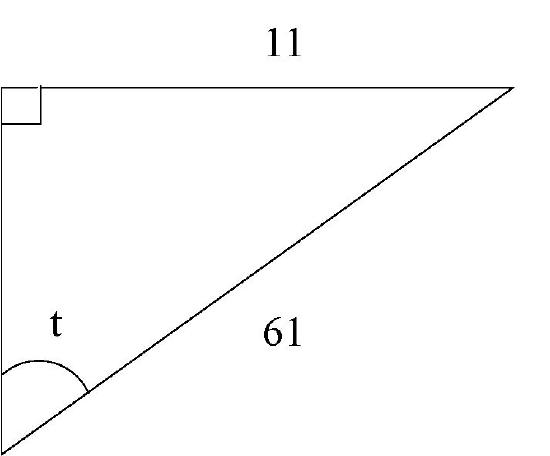
Answer

1. a) The unknown side is 6.
\(\sin \alpha = 3/5, \cos \alpha = 4/5, \tan \alpha = 3/4, \sec \alpha = 5/4, \csc \alpha = 5/3, \cot \alpha = 4/3\).

b) The unknown side is 15.
\(\sin \alpha = 15/17, \cos \alpha = 8/17, \tan \alpha = 15/8, \sec \alpha = 17/8, \csc \alpha = 17/15, \cot \alpha = 8/15\).

2. The unknown side is 60.
\(\cot t = 60/11, \sin t = 11/61, \sec t = 61/60\).

Exercise \(\PageIndex{2}\)

1. If \(\cos (\alpha)=\frac{3}{5}, \) and if \(\alpha +\beta= 90^{\circ},\) find \(\cot(\beta).\)

2. If \(\sec (\alpha)=2, \) and if \(\alpha +\beta= 90^{\circ},\) find \(\sin(\alpha),\, \csc(\beta)\) and \( \tan (\beta).\)

Answer

1. Since \(\alpha + \beta = 90^{\circ}\), \(\beta\) is the third angle of the triangle.
\(\cot \beta = 4/3\).

2. \(\displaystyle{\sin \alpha = \sqrt{3}, \csc \beta = 2, \tan \beta = \displaystyle \frac{\sqrt{3}}{3}}\)

Exercise \(\PageIndex{3}\)

Convert each of the angles given in degree measure to radian measure:

1. \(225^{\circ}\)

2. \(450^{\circ}\)

3. \(-210^{\circ}\)

4. \(175^{\circ}\)

5. \(1^{\circ}\)

Answer

1. \(\displaystyle{\displaystyle \frac{5\pi}{4}}\)

2. \(\displaystyle{\displaystyle \frac{5\pi}{2}}\)

3. \(\displaystyle{-\displaystyle \frac{7\pi}{6}}\)

4. \(\displaystyle{\displaystyle \frac{35\pi}{36}}\)

5. \(\displaystyle{\displaystyle \frac{\pi}{180}}\)

Exercise \(\PageIndex{4}\)

Convert each of the angles given in radian measure to degree measure:

1. \(2\)

2. \(\displaystyle \frac{\pi}{5}\)

3. \(\displaystyle \frac{-\pi}{12}\)

4. \(\displaystyle \frac{7\pi}{24}\)

5. \(\displaystyle \frac{11\pi}{6}\)

6. \(\displaystyle \frac{15\pi}{8}\)

Answer

1. \(\displaystyle{\displaystyle \frac{360^{\circ}}{\pi}}\)

2. \(36^{\circ}\)

3. \(-15^{\circ}\)

4. \(52.5^{\circ}\)

5. \(330^{\circ}\)

6. \(\displaystyle{337.5^{\circ}}\)

Exercise \(\PageIndex{5}\)

Find the reference angle for each of the following angles.

1. \(60^{\circ}\)

2. \(225^{\circ}\)

3. \(120^{\circ}\)

4. \(-120^{\circ}\)

5. \(\displaystyle \frac{\pi}{4}\)

6. \(\displaystyle \frac{4\pi}{3}\)

7. \(\displaystyle \frac{7\pi}{6}\)

8. \(\displaystyle \frac{5\pi}{6}\)

9. \(\displaystyle \frac{11\pi}{6}\)

10. \(3000^{\circ}\)

Answer

1. \(60^{\circ}\)

2. \(45^{\circ}\)

3. \(60^{\circ}\)

4. \(60^{\circ}\)

5. \(\displaystyle{\displaystyle \frac{\pi}{4}}\)

6. \(\displaystyle{\displaystyle \frac{\pi}{3}}\)

7. \(\displaystyle{\displaystyle \frac{\pi}{6}}\)

8. \(\displaystyle{\displaystyle \frac{\pi}{6}}\)

9. \(\displaystyle{\displaystyle \frac{\pi}{6}}\)

10. \(60^{\circ}\)

Exercise \(\PageIndex{6}\)

Complete the table below:

Answer

Exercise \(\PageIndex{7}\)

Determine the exact values of each of the following:

1. \(\sin \left(\displaystyle \frac{3 \pi}{2}\right)\)

2. \(\cos \left(\displaystyle \frac{11 \pi}{6}\right)\)

3. \(\sec(420^{\circ})\)

4. \(\tan(225^{\circ})\)

5. \(\tan \left(\displaystyle \frac{29\pi}{3}\right)\)

6. \(\sin \left(\displaystyle \frac{7 \pi}{6}\right)\)

7. \(\csc(-120^{\circ})\)

8. \(\sin \left(\displaystyle \frac{11 \pi}{3}\right)\)

Answer

1. \(-1\)

2. \(\displaystyle{\displaystyle \frac{\sqrt{3}}{2}}\)

3. \(2\)

4. \(1\)

5. \(-\sqrt{3}\)

6. \(\displaystyle{-\displaystyle \frac{2\sqrt{3}}{3}}\)

7. \(\displaystyle{-\displaystyle \frac{2\sqrt{3}}{3}}\)

8. \(\displaystyle{-\displaystyle \frac{\sqrt{3}}{2}}\)

Exercise \(\PageIndex{8}\)

1. If \(\sin (\alpha)=\displaystyle \frac{-3}{5},\, \) and \(\alpha \) is an angle in the third quadrant, then find

a) \( \cos (\alpha)\)

b) \( \tan (\alpha)\)

2. If \(\sec (\alpha)=\displaystyle \frac{17}{5},\) and \(270^{\circ}<\alpha < 360^{\circ} \(, then find

a) \( \cos (\alpha)\)

b) \( \sin (\alpha)\)

c) \( \tan (\alpha)\)

3.If \(\cos (t)=\displaystyle \frac{-12}{13},\) and \( \tan(t)>0,\) find

a) \( \sin(t)\)

b) \( \tan (t)\)

4.If \(\cot (\beta)=\displaystyle \frac{4}{3},\) and \( \sin(\beta)>0,\) find

a) \( \cos(\beta)\)

b) \( \csc (\beta)\)

5. If \(\tan (t)=\displaystyle \frac{1}{\sqrt{3}},\) and \( \cos(t)<0,\) find

a) \( \sin(t)\)

b) \( \cos (t)\)

6. If \(\csc (t)=2,\) and \( \cos(t)>0,\) find

a) \( \sin(t)\)

b) \( \tan (t)\)

c) \( \cos(t)\)

Answer

1. a) \(\cos \alpha = -4/5\), b) \(\tan \alpha = 3/4\).

2. a) \(\cos \alpha = 15/17\), b) \(\sin \alpha = -8/17\), c) \(\tan \alpha = -8/15\).

3. a) \(\sin t = -5/13\), b) \(\tan t = 5/12\).

4. a) \(\cos \beta = 4/5\), b) \(\csc \beta = 5/3\).

5. a) \(\sin t = -1/2\), b) \(\cos t = -\sqrt{3}/2\).

6. a) \(sin t = 1/2\), c) \(\tan t = -\sqrt{3}/3\), c) \(\cos t = -\sqrt{3}/2\).

Exercise \(\PageIndex{9}\)

Use the sum of difference formulas to determine the exact values of each of the following:

1. \(\sec(15^{\circ})\)

2. \(\sin(75^{\circ})\)

3. \(\tan(75^{\circ})\)

4. \(\csc \left(\displaystyle \frac{5 \pi}{12}\right)\)

5. \(\cos(105^{\circ})\)

6. \(\sin(165^{\circ})\)

7. \(\sin \left(\displaystyle \frac{ \pi}{12}\right)\)

Answer

1. \begin{eqnarray*}
\cos(15^{\circ}) &=& \cos(45^{\circ} - 30^{\circ}) \\
&=& \cos(45^{\circ})\cos(30^{\circ}) + \sin(45^{\circ})\sin(30^{\circ}) \\
&=& \left ( \displaystyle \frac{\sqrt{2}}{2} \right ) \left ( \displaystyle \frac{\sqrt{3}}{2} \right ) + \left ( \displaystyle \frac{\sqrt{2}}{2} \right ) \left ( \displaystyle \frac{1}{2} \right ) \\
&=& \displaystyle \frac{\sqrt{2}(\sqrt{3} + 1)}{4}
\end{eqnarray*}

Therefore, \(\displaystyle{\sec (15^{\circ}) = \displaystyle \frac{4}{\sqrt{2}(\sqrt{3} + 1)}}\).

2. \(\displaystyle{\sin (75^{\circ}) = \sin (45^{\circ} + 30^{\circ}) = \displaystyle \frac{\sqrt{2}(\sqrt{3} + 1)}{4}}\)

3. \(\displaystyle{\tan (75^{\circ}) = \displaystyle \frac{\sqrt{6}+2}{2\sqrt{3}-\sqrt{2}}}\)

4. \(\displaystyle{\sin \left ( \displaystyle \frac{5\pi}{12} \right ) = \sin \left ( \displaystyle \frac{3\pi}{12} + \displaystyle \frac{2\pi}{12} \right ) = \sin \left ( \displaystyle \frac{\pi}{4} + \displaystyle \frac{\pi}{6} \right ) = \displaystyle \frac{\sqrt{2}(\sqrt{3} + 1)}{4}}\)

Therefore, \(\displaystyle{\csc \left ( \displaystyle \frac{5\pi}{12} \right ) = \displaystyle \frac{4}{\sqrt{2}(\sqrt{3} + 1)}}\).

5. \(\displaystyle{\cos(105^{\circ}) = \displaystyle \frac{\sqrt{2}(\sqrt{3} - 1)}{4}}\)

6. \begin{eqnarray*}
\sin (165^{\circ}) &=& \sin (180^{\circ} - 15^{\circ}) \\
&=& \sin (180^{\circ}) \cos (15^{\circ}) - \cos (180^{circ}) \sin (15^{\circ}) \\
&=& \sin(15^{\circ}) \\
&=& \displaystyle \frac{\sqrt{2}(\sqrt{3}-1)}{4}
\end{eqnarray*}

7. \(\displaystyle{\sin \left ( \displaystyle \frac{\pi}{12} \right ) = \displaystyle \frac{\sqrt{2}(\sqrt{3} -1)}{4} }\)

Exercise \(\PageIndex{10}\)

1. If \(\sin (\alpha)=\displaystyle \frac{-3}{5},\) and \( \alpha \) is in the third quadrant, then determine \(\cos(2 \alpha), \sin(2 \alpha),\) and \(\tan(2 \alpha).\)

2. If \(\sec (\alpha)=\displaystyle \frac{17}{5},\) and \( 270^{\circ} < \alpha < 360^{\circ} \), then find \(\tan(2 \alpha).\)

3. If \(\tan (\beta)=\displaystyle \frac{1}{\sqrt{3}},\) and \( \cos(\beta)<0,\) find \(\sin(2 \beta)\) and \(\cos(2 \beta).\)

4. If \(\csc (t)=2,\) and if \(\displaystyle \frac{\pi}{2} < t < \pi,\) find \(\sin(2t), \csc(2t),\sec(2t)\) and \( \tan(2t).\)

5. If \(\sin (\alpha)=\displaystyle \frac{-4}{5},\) and \( \alpha \) is in the third quadrant, then find \(\cos( \alpha/2), \sin( \alpha/2),\) and \(\tan( \alpha/2).\)

6. If \(\tan (t)=\displaystyle \frac{1}{\sqrt{3}},\) and \( \cos(t)<0,\) find \(\sin(t/2),\cos(t/2)\) and \(\tan(t/2).\)

7. If \(\csc (t)=-2,\) and if \(\displaystyle \frac{3\pi}{2} < t < 2\pi,\) find \(\cos(t/2),\) and \( \tan(t/2).\)

8. If \(\cot (\alpha)=-1,\) and if \( \sin(\alpha) >0 \), then find \(\cos( \alpha/2), \sin( \alpha/2),\) and \(\tan( \alpha/2).\)

9. If \(\sin (\alpha)=\frac{11}{61},\) and \( \alpha \) is in the first quadrant, then find \(\csc( \alpha/2),\) and \(\sec( \alpha/2).\)

Answer

1. \(\cos (2\alpha) = \cos^2 \alpha - \sin^2 \alpha = 7/25\)
\(\sin (2\alpha) = 2\sin \alpha \cos \alpha = 24/25\)
\(\displaystyle{\tan (2\alpha) = \displaystyle \frac{2\tan \alpha}{1-\tan^2 \alpha}} = 24/7\)

2. \(\tan (2\alpha) = -240/161\)

3. \(\sin (2\beta) = \sqrt{3}/2\)
\(\cos (2\beta) = 1/2\)

4. \(\sin (2t) = -\sqrt{3}/2\)
\(\cos (2t) = 1/2\)
\(\sec (2t) = 2\)
\(\tan (2t) = - \sqrt{3}\)

5. \(\displaystyle{\cos (\alpha /2) = \pm \sqrt{\displaystyle \frac{1+\cos \alpha}{2}} = -\displaystyle \frac{2\sqrt{5}}{5}}\), `-' because the angle is in the third quadrant.
\(\displaystyle{\sin (\alpha /2) = \pm \sqrt{\displaystyle \frac{1-\cos \alpha}{2}} = - \displaystyle \frac{4\sqrt{5}}{5} }\)
\(\displaystyle{\tan (\alpha /2) = \displaystyle \frac{1-\cos \alpha}{\sin \alpha} = -2}\)

6. \(\displaystyle{\sin (t/2) = -\sqrt{\displaystyle \frac{2 + \sqrt{3}}{4}}}\)
\(\displaystyle{\cos (t/2) = -\sqrt{\displaystyle \frac{2 - \sqrt{3}}{4}}}\)
\(\displaystyle{\tan (t/2) = -2- \sqrt{3}}\)

7. \(\displaystyle{\cos (t/2) = \sqrt{\displaystyle \frac{2 + \sqrt{3}}{4}}}\)
\(\displaystyle{\tan (t/2) = -2 + \sqrt{3}}\)

8. \(\displaystyle{\sin (\alpha/2) = \sqrt{\displaystyle \frac{2 + \sqrt{2}}{4}}}\)
\(\displaystyle{\cos (\alpha/2) = -\sqrt{\displaystyle \frac{2 - \sqrt{2}}{4}}}\)
\(\displaystyle{\tan (\alpha/2) = 1 + \sqrt{2}}\)

9. \(\displaystyle{\csc (\alpha/2) = \sqrt{122}}\)
\(\displaystyle{\sec (\alpha/2) = \sqrt{\displaystyle \frac{122}{121}}}\)

Exercise \(\PageIndex{11}\)

For each of the following, determine the amplitude, phase shift and period. Use this information to sketch the graph.

1. \(y=4\sin(2x+\pi/3)\)

2. \(y=\displaystyle \frac{1}{2}\cos(5x-\pi/4)\)

3. \(y=-2\cos(x/3)\)

4. \(y=2\tan(3x+\pi/2)\)

5. \(y=-3\sin(4x)\)

6. \(y=\displaystyle \frac{4}{3}\cos(2x)\)

Answer

1. Amplitude: \(4\); Phase shift: \(\displaystyle\frac{\pi}{3}\); Period: \(\pi\).

2. Amplitude: \(\displaystyle\frac{1}{2}\); Phase shift: \(\displaystyle\frac{\pi}{4}\); Period: \(\displaystyle\frac{2\pi}{5}\).

3. Amplitude: \(2\); Phase shift: none; Period: \(6\pi\).

4. Amplitude: none; Phase shift: \(\displaystyle\frac{\pi}{2}\); Period: \(\displaystyle\frac{\pi}{3}\).

5. Amplitude: \(3\); Phase shift: none; Period: \(\displaystyle\frac{\pi}{4}\).

6. Amplitude: \(\displaystyle\frac{4}{3}\); Phase shift: none; Period: \(\displaystyle\frac{\pi}{2}\).

Exercise \(\PageIndex{12}\)

Solve each of the following trigonometric equations in the interval indicated.

1. \( 2 \cos (x) +1=0, \,\, [0^{\circ},360^{\circ})\)

2. \( 2 \tan(x) \sin(x)+ 2 \sin(x)-\tan(x)-1=0,\,\, [0,\pi]\)

3. \( \csc^2 (t) -4=0, \,\, [0^{\circ},180^{\circ}]\)

4. \( \sin^2 (t) -3=0, \,\, [0^{\circ},360^{\circ})\)

5. \( 2 \cos^2(x)-3 \cos(x)+1=0,\,\, [0, 2 \pi)\)

6. \( 2\sin^2 (x) +3 \sin(x)+1=0, \,\, [0^{\circ},360^{\circ})\)

7. \( (2\sin (x) -1)(\tan(x)+1)=0, \,\, [0^{\circ},360^{\circ})\)

8. \( \sin(x) (2\cos (x) +\sqrt{3})(\tan(x)-\sqrt{3})=0, \,\, [0^{\circ},360^{\circ})\)

9. \( \sin(2x)=0,\, \cos(2x)=0,\, [0,2 \pi)\)

Answer

1. \(x = 120^{\circ}, 240^{\circ}\)

2. Factor by grouping to get \(\tan x + 1 = 0 \) or \(2\sin x -1 = 0\).
\(\tan x + 1 = 0\) yields the solution \(x = 3\pi/4\) and \(2\sin x -1 = 0\) yields the solutions \(x = \pi/6, 5\pi /6\).

3. Need to solve \(\csc t = \pm 2\).
The solutions are \(t = 60^{\circ}, 150^{\circ}\).

4. Need to solve \(\sin t = \pm\sqrt{3}/2\).
The solutions are \(t = 60^{\circ}, 120^{\circ}, 240^{\circ}, 300^{\circ}\).

5. Need to solve \(\cos x = 1, 1/2\).
The solutions are \(x = 0, \pi/3, 5\pi/3\).

6. Need to solve \(\sin x = -1, -1/2\).
The solutions are \(x = 270^{\circ}, 210^{\circ}, 330^{\circ}\).

7. Need to solve \(\sin x = 1/2\) and \(\tan x = -1\).
The solutions are \(x = 30^{\circ}, 150^{\circ}, 135^{\circ}, 315^{\circ}\).

8. Need to solve \(\sin x = 0, \cos x = -\sqrt{3}/2, \tan x = \sqrt{3}\).
The solutions are \(x = 0^{\circ}, 180^{\circ}, 150^{\circ}, 210^{\circ}, 60^{\circ}, 240^{\circ}\).

9. The solutions are \(x = 0, \pi/2, \pi, 3\pi/2, \pi/4, 3\pi/4, 5\pi/4, 7\pi/4\).

Exercise \(\PageIndex{13}\)

Given that \(\tan(\alpha/2)=t,\) express each of the following in terms of \(t\):

1. \(\sin( \alpha/2)\)

2. \(\cos( \alpha/2)\)

3. \(\tan( \alpha/2)\)

4. \(\sin( \alpha)\)

5. \(\cos( \alpha)\)

6. \(\tan( \alpha)\)

Answer

Construct a right-angled triangle with \(\alpha/2\) as one of the angles.
Then the opposite side it \(t\) and the adjacent side is \(1\). Using Pythagoras' theorem, we obtain a hypotenuse of \(\sqrt{t^2+1}\).

Therefore, \(\displaystyle{\sin (\alpha/2) = \displaystyle \frac{t}{\sqrt{t^2+1}}}\) and \(\displaystyle{\cos (\alpha/2) = \displaystyle \frac{1}{\sqrt{t^2+1}}}\).

Using \(\sin (\alpha) = 2\sin(\alpha/2) \cos (\alpha/2)\), we obtain \(\displaystyle{\sin (\alpha) = \displaystyle \frac{2t}{t^2+1}}\).

Using \(\cos (\alpha) = 2\cos^2 x -1\), we obtain \(\displaystyle{\cos (\alpha) = \displaystyle \frac{-t^2+2t-1}{t^2+1}}\).

Therefore, \(\displaystyle{\tan(\alpha) = \displaystyle \frac{2t}{-t^2+2t-1}}\).

Note: This solution assumes \(0 \leq t <\pi/2\). If \(t\) was in another quadrant, how does this effect the solution?

Exercise \(\PageIndex{14}\)

In each of the following, find other information about the triangle \(ABC\), using the information provided:

1. \(A=130^{\circ},\, B=20^{\circ}, \, b=10\)

2. \(B=120^{\circ},\, C=30^{\circ}, \, a=16\)

3. \(C=30^{\circ},\, a=24, \, b=34\)

4. \(C=108^{\circ},\, a=10, \, b=15\)

5. \(a=12,\,b=17,\,c=19\)

6. \(A=40^{\circ},\, a=7, \, c=10\)

7. \(A=40^{\circ},\, a=12, \, c=10\)

Answer

1. \( C = 108^{\circ} - 130^{\circ} - 20^{\circ} = 30^{\circ} \)

\( a = \displaystyle \frac {b\sin(130^{\circ})}{\sin(20^{\circ})} = 22.398 \)

\( c = \displaystyle \frac {b\sin(30^{\circ})}{\sin(20^{\circ})} = 14.619 \)

2. \( A = 180 ^{\circ} - 120 ^{\circ} - 30 ^{\circ} = 30 ^{\circ} \)

\( b = \displaystyle \frac {a\sin(120^{\circ})}{\sin30^{\circ})} = 27.713 \)

\( c = \displaystyle \frac {a\sin(30^{\circ})}{sin(30^{\circ})} = 16 \)

3. \( c = \sqrt{a^2 + b^2 - 2ab\cos(30^{\circ})} = 17.851 \)

\( A = \arccos\left(\displaystyle \frac {c^2 + b^2 - a^2}{2cb}\right) = 107.76^{\circ} \)

\( B = \arccos\left(\displaystyle \frac {c^2 + a^2 - b^2}{2ca}\right) = 42.24^{\circ} \)

4. \( c = \sqrt{a^2 + b^2 - 2ab\cos(108^{\circ})} = 20.438^{\circ} \)

\( A = \arccos\left(\displaystyle \frac {c^2 + b^2 - a^2}{2cb}\right) = 27.73^{\circ} \)

\( B = \arccos\left(\displaystyle \frac {c^2 + a^2 - b^2}{2ca}\right) = 44.27^{\circ} \)

5. \( A = \arccos\left(\displaystyle \frac {c^2 + b^2 - a^2}{2cb}\right) = 38.44^{\circ} \)

\( B = \arccos\left(\displaystyle \frac {c^2 + a^2 - b^2}{2ca}\right) = 61.73^{\circ} \)

\( C = \arccos\left(\displaystyle \frac {a^2 + b^2 - c^2}{2ab}\right) = 79.84^{\circ} \)

6. \( C = \arcsin\left(\displaystyle \frac {c\sin(40^{\circ})}{a}\right) = 66.67^{\circ} \)

\( B = 180^{\circ} - 40^{\circ} - 66.67^{\circ} = 73.33^{\circ} \)

\( b = \displaystyle \frac {a\sin(73.33^{\circ})}{\sin(40^{\circ})} = 10.432 \)

7. \( C = \arcsin\left(\displaystyle \frac {c\sin(40^{\circ})}{a}\right) = 32.39^{\circ} \)

\( B = 180^{\circ} - 40^{\circ} - 32.39^{\circ} = 107.61^{\circ} \)

\( b = \displaystyle \frac {a\sin(107.61^{\circ})}{\sin(40^{\circ})} = 17.794 \)

Exercise \(\PageIndex{15}\)

1. A ladder \(10\) meters long is leaning against the side of a building. It makes an angle of \(75^{\circ}\) with the ground. How far up the side of the building does the ladder reach?

2. A man \(6\) ft tall on the ground \(12\) ft away from a lamp-post. The light come from the lamp casts a shadow which is \(8\) ft long. Determine the height of the lamp-post.

3. From the top of a light house, \(40\) metres above sea-level, the angle of depression to a boat is observed to be \(25^{\circ}.\) Find the horizontal distance between the boat and the light house.

Answer

1. The ladder reaches up \(10 \sin (75^{\circ})\) m up the wall.

2. Using similar triangles, the lamppost is \(15\) ft high.

3. The horizontal distance is \(40 \tan (25^{\circ})\) m.

Logarithms and Exponents

Exercise \(\PageIndex{1}\)

Which of the following functions are exponential functions? If the function is exponential, determine its base.

1. \(f(x)=6^x\)

2. \(f(x)=x^6\)

3. \(f(x)=2^{-3x}\)

4. \(f(x)=\sqrt{(5^{3x})}\)

Answer

1. The function is exponential and its base is \(6\).

2. The function is not exponential.

3. The function is exponential and its base is \(2\).

4. The function is exponential and its base is \(5\).

Exercise \(\PageIndex{2}\)

Sketch the graphs of each of the following:

1. \(y=3^x\)

2. \(y=3^{-2x}\)

3. \(y=5^x-7\)

4. \(y=2^{x-4}+1\)

Answer

1.

2.

3.

4.

Exercise \(\PageIndex{3}\)

Solve each of the following exponential equations:

1. \(3^{(2x-1)}=27^{7/3}\)

2. \(8^{-2x}=\displaystyle \frac{1}{64}\)

3. \(81^{x}=21^{2-x}\)

4. \(7^{x-2}=\displaystyle \frac{1}{343}\)

5. \(2^{7x}=\displaystyle \frac{1}{\sqrt{2}}\)

6. \(10^{2x-1}=5\)

7. \(3^{x}=17\)

8. \(4^{x-2}=2^{1-x}\)

9. \(2^{x}=21\)

10. \((2^{3x}-8)(2^{5x}-4)=0\)

11. \(3^{x}+3^{-x}=2\)

12. \(3^{x}+3^{-x}=\displaystyle \frac{10}{3}\)

Answer

1. Write each side of the equation as a same base (in this case 3).
\[3^{2x-1} = 3^{3(7/3)} = 3 ^ 7\]
\[ x = 4 \]

2. Since we have \(8^{-2x} = 8^{-2}\), then \(x = 1\)

3. Since we have \(3^{4x} = 3^{6-3x}\), then \(x = 6/7\).

4. Since we have \(7^{x-2} = 7^{-3}\), then \(x = -1\).

5. Since we have \(2^{7x} = 2^{-1/2}\), then \(x = -1/14\).

6. Since \(10\) and \(5\) cannot be neatly written in terms of the same base, we will use logarithms to solve.
\begin{eqnarray*}
10^{2x-1} &=& 5 \\
\log (10^{2x-1}) &=& \log (5)\\
2x - 1 &=& \log (5) \\
x &=& (\log (5) +1)/2
\end{eqnarray*}

7. \(x= \log_3 (17)\)

8. Since \(2^{2x+4} = 2^{1-x}\), then \(x = 1\).

9. \(x = \log_{2} (21)\)

10. Since \(2^{3x} = 8\) or \(2^{5x} = 4\), then \(x = 1\) or \(\displaystyle \frac{2}{5}\).

11. Multiply both sides by \(3^{x}\) to obtain \(3^{2x} + 1 = 2\cdot 3^{x}\). Bring all the terms to one side and recognize that this is a hidden quadratic.

Therefore, let \(3^x = 1\) and \(x = 0\).

12. \(x = -1, 1\)

Exercise \(\PageIndex{4}\)

Express each of the following in logarithmic form:

1. \(2^{x}=y\)

2. \(5^{-3}=\displaystyle \frac{1}{125}\)

3. \(4^{x+y}=15\)

4. \(29^{0}=1\)

5. \(x^{3}=2y\)

6. \(4^{1}=4\)

Answer

1. \(x = \log_2 (y)\)

2. \(\displaystyle{-3 = \log_5 (\displaystyle \frac{1}{125})}\)

3. \(x+y = \log_4(15)\)

4. \(0 = \log_{29} (1)\)

5. \(3 = \log_{x} (2y)\)

6. \(1 = \log_4 (4)\)

Exercise \(\PageIndex{5}\)

Express each of the following in exponential form:

1. \(x= \log_2(y)\)

2. \(y= \log_x(4)\)

3. \(\log_5(\displaystyle \frac{1}{125})=-3\)

4. \(\log_7(7)=1\)

5. \(\log_3(1)=0\)

6. \(\log(y)=2\)

7. \(\log(.001)=-3\)

8. \(\log_{1/3}(81)=-4\)

9. \(\log_3(y+z)=x+y\)

10. \(\log(x-5)=2\)

Answer

1. \(2^x = y\)

2. \(4 = x^y\)

3. \(\displaystyle{\displaystyle \frac{1}{125} = 5^{-3}}\)

4. \(7 = 7^1\)

5. \(1 = 3^{0}\)

6. \(y = 10^2\)

7. \(0.001 = 10^{-3}\)

8. \(81 = (1/3)^{-4}\)

9. \(y+z = 3^{x+y}\)

10. \(x-5 = 10^2\)

Exercise \(\PageIndex{6}\)

Sketch each of the following graphs and compare them to the graphs of the exponential function given.

1. \(y= \log_4(x)\) compare with \(y=4^x.\)

2. \(y= \log(x)\) compare with \(y=10^x.\)

Answer

1. \(y= \log_4(x)\)

\(\textcolor{red}{y=4^x}\)

2. \(\textcolor{blue}{y= \log(x)}\)

\(\textcolor{green}{y=10^x}\)

Exercise \(\PageIndex{7}\)

Express as a single logarithm:

1. \(2 \log_2(x)-5 \log_2(x-2)+\displaystyle \frac{1}{2} \log_2(x^2+1)\)

2. \(\displaystyle \frac{1}{3} \log(2x-1)-52\log(x)-7 \log (1+x)+\displaystyle \frac{2}{3} \log(5x+12)\)

Answer

1. \(\displaystyle{\log_2 \left ( \displaystyle \frac{x^2\sqrt{x^2+1}}{(x-2)^5} \right )}\)

2. \(\displaystyle{\log \left ( \displaystyle \frac{\sqrt[3]{(2x-1)(5x+12)^2}}{x^2(1+x)^7}\right )}\)

Exercise \(\PageIndex{8}\)

Express as a sum or difference of logarithms:

1. \( \log_2 \displaystyle \frac {x^2 \sqrt{(x^2+1)}}{(x-2)^5}\)

2. \( \log \displaystyle \frac {\sqrt[3]{(2x-1)}\, \sqrt[3]{(5x+12)^2}}{x^2(1+x)^7}\)

3. \( \log_5\displaystyle \frac {x(1-x)^2}{(2-x)^4}\)

4. \( \log_{1/2}\displaystyle \frac {x^2(1+x)^{2/7}}{4(x-2)^3}\)

Answer

1. \(\displaystyle{2\log_2 (x) + \displaystyle \frac{1}{2}\log_2 (x^2+1) - 5\log_2(x-2)}\)

2. \(\displaystyle{\displaystyle \frac{1}{3}\log (2x-1) + \displaystyle \frac{2}{3} \log (5x+12) - 2\log (x) - 7\log (1+x)}\)

3. \(\displaystyle{\log_5 x + 2\log_5 (1-x) - 4\log_5 (2-x)}\)

4. \(\displaystyle{2\log_{1/2}x + \displaystyle \frac{2}{7}\log_{1/2}(1+x) -2 - 3\log_{1/2}(x-2)}\)

Exercise \(\PageIndex{9}\)

Simplify each of the following:

1. \(\log_232\)

2. \(\log (0.001)\)

3. \(\log_x x^3\)

4. \(\log_2 4-\log_4 16\)

Answer

1. \(\log_2(32) = \log _2(2^5) = 5\)

2. \(\log(0.001) = \log (10^{-3}) = -3\)

3. \(\log_x (x^3) = 3\)

4. \(\log_2 (4) - \log_4(16) = \log_2(2^2) - \log_4(4^2) = 0\)

Exercise \(\PageIndex{10}\)

Solve each of the following equations:

1. \(\log_3 x=-2\)

2. \(\log 1000=x\)

3. \(\log_x 16=4\)

4. \(\log (0,1)=2x\)

5. \(\log_2 (3 x+1)- \log_2(x-8)=-1\)

6. \(\log_x 4=-1\)

7. \(\log x- \log(2x-1)=0\)

8. \(\log_5 x- \log_5(x+7)=\log_5 2- \log_5(x-3)\)

9. \(2\log_2 x- \log_2 \left(x-\displaystyle\frac{1}{3}\right)=\log_2 3 -1\)

10. \(\log_{3 \sqrt{2}} x+ \log_{3 \sqrt{2}} (x-3)=2\)

11. \(\log_{3 \sqrt{2}} x+ \log_{3 \sqrt{2}} (x+3)=2\)

Answer

1. \(x= 3^{-2} = \displaystyle \frac {1}{9}\)

2. \(x=-3\)

3. \(x = 2\), since \(2^4 = 16\)

4. \(x=\displaystyle \frac{-1}{2}\)

5. \begin{eqnarray*}
\log_2(3x+1) - \log_2(x-8) &=& -1 \\
\log_2 \left ( \displaystyle \frac{3x+1}{x-8} \right )&=& -1 \\
\displaystyle \frac{3x+1}{x-8} &=& 2^{-1} \\
6x+2 &=& x-8 \\
x &=& -2
\end{eqnarray*}

But \(x = -2\) is extraneous because if we \(x=-1\) in the original equation, we get the logarithm of a negative number which is undefined. Therefore, the equation has no solution.

6. \(x=\displaystyle \frac {1}{4}\)

7. \begin{eqnarray*}
\log x - \log (2x-1) &=& 0 \\
\log x &=& \log (2x-1) \\
x &=& 2x-1 \\
x &=& 1
\end{eqnarray*}

8. \begin{eqnarray*}
\log_5(x) - \log_5(x+7) &=& \log_5 (2) - \log_5 (x-3) \\
\log_5 \left ( \displaystyle \frac{x}{x+7} \right ) &=& \left ( \displaystyle \frac{2}{x-3} \right ) \\
\displaystyle \frac{x}{x+7} &=& \displaystyle \frac{2}{x-3} \\
x(x-3) &=& 2(x+7) \\
x &=& 7, -2
\end{eqnarray*}

\(x= -2\) is an extraneous solution.
Solution: \(x = 7\).

9. \begin{eqnarray*}
2\log_2 (x) - \log_2(x-1/3) &=& \log_2 (3) -1 \\
2\log_2 (x) - \log_2(x-\displaystyle \frac{1}{3}) -\log_2 (3) &=& -1 \\
\log_2 \left ( \displaystyle \frac{x^2}{3(x-\displaystyle \frac{1}{3})} \right ) &=& -1 \\
\displaystyle \frac{x^2}{3x-1} &=& \displaystyle \frac{1}{2} \\
x &=& 1, 1/2
\end{eqnarray*}

10.

\begin{eqnarray*}
\log_{3\sqrt{2}} (x) + \log_{3\sqrt{2}} (x-3) &=& 2 \\
\log_{3\sqrt{2}} (x(x-3)) &=& 2 \\
x(x-3) &=& 18 \\
x &=& -3, 6
\end{eqnarray*}

\(x = -3\) is an extraneous solution.
Solution: \(x = 6\).

11. \begin{eqnarray*}
\log_{3\sqrt{2}} (x) + \log_{3\sqrt{2}} (x+3) &=& 2 \\
\log_{3\sqrt{2}} (x(x+3)) &=& 2 \\
x(x+3) &=& 18 \\
x &=& 3, -6
\end{eqnarray*}

\(x = -6\) is an extraneous solution.
Solution: \(x = 3\).