Common Mistakes

The purpose of this page is to alert the reader to the common mistakes which might be made in simple calculations. The reader should care fully analyze each statement, making sure that they can justify the correct statement.

Answer true or false for each of the statements given below. If the statement is false, write the correct version.

Exercise \(\PageIndex{1}\)

1. \(\sqrt{(a+b)}=\sqrt{a}+\sqrt{b}\)

Answer

False. Leave \(\sqrt{a+b}\) as is. It cannot be simplified any further. 

Exercise \(\PageIndex{2}\)

2. \( a^{-1/2}=\displaystyle \frac{1}{a^2}\)

Answer

False. \(\displaystyle{a^{-1/2} = \displaystyle \frac{1}{\sqrt{a}}}\)

Exercise \(\PageIndex{3}\)

3. \((a+b)^2=a^2+b^2\)

Answer

False. \((a+b)^2 = a^2 + 2ab+b^2\)

Exercise \(\PageIndex{4}\)

4. \(-(-2)^2=4\)

Answer

False. \(-(-2)^2 = -4\)

Exercise \(\PageIndex{5}\)

5. \(-3^4=81\)

Answer

False. \(-3^4 = -(3^4) =-81\)

Exercise \(\PageIndex{6}\)

6. \(2^3=6\)

Answer

False. \(2^3 = 8\)

Exercise \(\PageIndex{7}\)

7. \(\displaystyle \frac{a+b}{c}=\displaystyle {\frac{a}{c}+\frac{b}{c}}\)

Answer

True.

Exercise \(\PageIndex{8}\)

8. \(\displaystyle \frac{c}{a+b}=\displaystyle {\frac{c}{a}+\frac{c}{b}}\)

Answer

False. \(\displaystyle{\displaystyle \frac{c}{a+b}}\) cannot be simplified any further.

Exercise \(\PageIndex{9}\)

9. \(\displaystyle \frac{5h}{h(h+2)}=\displaystyle \frac{4h}{h+2}\)

Answer

False. \(\displaystyle{\displaystyle \frac{5h}{h(h+2)} = \displaystyle \frac{5}{h+2}}\)

Exercise \(\PageIndex{10}\)

10.\(\displaystyle \frac{0}{3}\) is not defined.

Answer

False. \(\displaystyle{\displaystyle \frac{0}{3} = 0}\)

Exercise \(\PageIndex{11}\)

11. \(\displaystyle \frac{5}{0}=0\)

Answer

False. \(\displaystyle{\displaystyle \frac{5}{0}}\) is undefined.

Exercise \(\PageIndex{12}\)

12. \(\displaystyle \frac{xy}{2}=\displaystyle \frac{x}{2}\frac{y}{2}\)

Answer

False. \(\displaystyle \frac{xy}{2}\) cannot be simplified any further.

Exercise \(\PageIndex{13}\)

13. \(-2x=0 \Rightarrow x=2\)

Answer

False. \(x= 0\)

Exercise \(\PageIndex{14}\)

14. \(-3x=2 \Rightarrow x=2+3=5\)

Answer

False. \(x= \displaystyle \frac {-2}{3}\)

Exercise \(\PageIndex{15}\)

15.  \(x^2+1=0 \Rightarrow x=\pm 1\)

Answer

False. \(x^2+1 = 0\) does not have any real solutions. It does have complex solutions \(x = \pm i\). 

Exercise \(\PageIndex{16}\)

16. \((x-2)^2=0 \Rightarrow x=\pm 2\)

Answer

False. \(x = 2\)

Exercise \(\PageIndex{17}\)

17. The solutions of the quadratic equation \(c^2+5c+6=0\) are given by \(c=\pm \sqrt{(5c-6)}\).

Answer

False. Factor the quadratic \((c-5)(c+1) = 0\). Then \(c= 5, -1\). 

Exercise \(\PageIndex{18}\)

18. \((c-1)(c-3)=1 \Rightarrow c-1= 1,\) or \(c-3=1\)

Answer

False. This is true if \((c-1)(c-3) = 0\) (not \(1\)). 

Exercise \(\PageIndex{19}\)

19. \(\displaystyle  2\left(\frac{4}{3}\right)=\frac{8}{6}\)

Answer

False. \(\displaystyle{2 \cdot \displaystyle \frac{4}{3} = \displaystyle \frac{8}{3}}\)

Exercise \(\PageIndex{20}\)

20. \(\displaystyle \frac{\displaystyle\frac{1}{2}}{3}=\frac{3}{2}\)

Answer

False. \(\displaystyle{ \displaystyle \frac{\displaystyle \frac{1}{2}}{3} = \displaystyle \frac{1}{6}}\)

Exercise \(\PageIndex{21}\)

21. The only solution of the quadratic equation \(x^2-2x=0\) is \(x=2\).

Answer

False. \(x=0\) is also a solution. 

Exercise \(\PageIndex{22}\)

22. \(\displaystyle \frac{x-1}{x+5}=0 \Rightarrow x-1=0,\) or \(x+5=0\)

Answer

False. Only \(x-1=0\) (if \(x+5=0\), this would cause division by zero).

Exercise \(\PageIndex{23}\)

23. \(\displaystyle \frac{3x}{2}=\displaystyle \frac{3}{2} \,x\)

Answer

True.

Exercise \(\PageIndex{24}\)

24. By factoring an expression such as \(x^2-4,\) we mean: Solve \(x^2-4=0\) which yields \(x^2=4 \Rightarrow x=\pm 2\)

Answer

False. By factoring an expression such as \(x^2-4\), we mean: \(x^2-4 = (x-2)(x+2)\). 

Exercise \(\PageIndex{25}\)

25. The conjugate of \(\sqrt{(x+1)}+2\) is \(\sqrt{(x-1)}-2\). 

Answer

False. The conjugate is \(\sqrt{x+1} -2\).

Exercise \(\PageIndex{26}\)

26. \(\left(\sqrt{(x+1)}\right)^2=(x+1)^2\)

Answer

False. \((\sqrt{x+1})^2 = x+1\)

Exercise \(\PageIndex{27}\)

27. \(x-1\) is the same as \(1-x\)

Answer

False. \(x-1\) is the same as \(-(1-x)\).

Exercise \(\PageIndex{28}\)

28. \(\displaystyle \frac {(x-1)(x-3)}{(3-x)}=x-1\)

Answer

False. \(\displaystyle{\displaystyle \frac{(x-1)(x-3)}{3-x} =-(x-1), x \neq 3}\)

Exercise \(\PageIndex{29}\)

29. \(-x-1=-(x-1)\)

Answer

False. \(-x-1 = -(x+1)\)

Exercise \(\PageIndex{30}\)

30. \(\displaystyle \frac{4x+4}{x+8}=\frac{4+4}{9}=\displaystyle \frac{8}{9}\)

Answer

False. \(\displaystyle{ \displaystyle \frac{4x+4}{x+8} = \displaystyle \frac{4(x+1)}{x+8} }\), which cannot be simplified any further. 

Exercise \(\PageIndex{31}\)

31. \(\displaystyle \frac{3h}{h}=2h\)

Answer

False. \(\displaystyle{\displaystyle \frac{3h}{h} = 3, h\neq 0 }\)

Exercise \(\PageIndex{32}\)

32. \(-(x^2-5x+1)=-x^2-5x+1\)

Answer

False. \(-(x^2-5x+1) = -x^2+5x-1\)

Exercise \(\PageIndex{33}\)

33. \(\displaystyle \frac{1}{3x}+ \displaystyle \frac{3}{7x}=\displaystyle \frac{4}{7x}\)

Answer

False. \(\displaystyle{\displaystyle \frac{1}{3x} + \displaystyle \frac{3}{7x} = \displaystyle \frac{16}{21x}    }\)

Exercise \(\PageIndex{34}\)

34. If \(f(x)=x^2,\) then \(f(2+h)=4+h\)

Answer

False. \(f(2+h) = (2+h)^2 = 4+4h+h^2\)

Exercise \(\PageIndex{35}\)

35. The slope of the straight line which is perpendicular to the straight line \(2x-3y+11=0\) is \(3/2\).

Answer

False. The slope would be \(\displaystyle \frac {-3}{2}\).

Exercise \(\PageIndex{36}\)

36. Given that \(A=(1,5)\) and \(B=(7,3),\) the midpoint of the line segment \(AB\) is the point \(M\) is given by 
$$M=\left( \displaystyle \frac{1-7}{2},\displaystyle \frac{5-3}{2} \right)$$

Answer

False. The midpoint would be \(M = \left ( \displaystyle \frac{1+7}{2}, \displaystyle \frac{5+3}{2} \right )\).

Exercise \(\PageIndex{37}\)

37. \(\sqrt{(4x^2+1)}=2x+1\)

Answer

False. \(\sqrt{4x^2+1}\) cannot be simplified any further. 

Exercise \(\PageIndex{38}\)

38. \(\sin (\cos(x))= \sin (x) \cos (x)\)

Answer

False. \(\sin (\cos x)\) cannot be simplified any further. 

Exercise \(\PageIndex{39}\)

39. \begin{eqnarray*} 
x( \cos (x) + \sin (x)) &= & \cos (x^2)+ \sin(x^2)\\
&=& x^2 \cos + x^2 \sin\\
\end{eqnarray*}

Answer

False. \(x(\cos x + \sin x) = x\cos x + x \sin x$\) 

Exercise \(\PageIndex{40}\)

40. \(1- \cos (8x)=2 \sin^2 (8x)\)

Answer

False. \(1-\cos (8x)\) cannot be simplified any further. 

Exercise \(\PageIndex{41}\)

41. \(\tan (x^2)= \tan\,\, x^2\)

Answer

False. \(\tan (x^2)\) cannot be simplified any further. Furthermore, \(\tan (x^2)\) is the composition of \(\tan (x)\) with \(x^2\). It is not the same as multiplication. 

Exercise \(\PageIndex{42}\)

42. \(\sqrt{\sqrt{a}}=a\)

Answer

False. \(\sqrt{\sqrt{a}} = a^{1/4}\)

Exercise \(\PageIndex{43}\)

43. \(\sqrt[3]{8^2}=\left(\sqrt[3]{8} \right)^2\)

Answer

True.

Exercise \(\PageIndex{44}\)

44. \(\displaystyle \frac{\sqrt{27}}{9}=\sqrt{9}=3\)

Answer

False. \(\displaystyle{ \displaystyle \frac{\sqrt{27}}{9} = \displaystyle \frac{3\sqrt{3}}{9} = \displaystyle \frac{\sqrt{3}}{3}   }\)

Exercise \(\PageIndex{45}\)

45. \(a^2-1=-a\)

Answer

False. This is an equation that can be solved for \(a\) but it is not true in general.

Exercise \(\PageIndex{46}\)

46. \(a^{-3/4}=\displaystyle \frac{1}{a^{4/3}}\)

Answer

False. \(\displaystyle{a^{-3/4} = \displaystyle \frac{1}{a^{3/4}}}\)

Exercise \(\PageIndex{47}\)

47. \(\log ^2 x= 2 \log x\)

Answer

False. \(\log_2\hspace{3mm}^2 (x) = (\log_2 x)^2\)

Exercise \(\PageIndex{48}\)

48. \(\cos^3 x=\cos x^3\)

Answer

False. \(\cos^3 (x) = (\cos x)^3\)

Exercise \(\PageIndex{49}\)

49. Recall that \(\log 1=0.\) Then, \(\log(-1)=- \log 1=0.\)

Answer

False. \(\log_a (b)\) where \(b\) is a negative number is always undefined. Therefore, \(\log (-1)\) is undefined. 

Exercise \(\PageIndex{50}\)

50. \((x-1)^2-(y+1)^2=4\) represents a circle centered at \((1,-1)\) and having radius \(2\).

Answer

False. The equation represents a hyperbola centered at \((1,-1)\). 

Exercise \(\PageIndex{51}\)

51. \(y^2-3x+1=0\) is an equation of a straight line with slope \(3.\)

Answer

False. \(y-3x+1=0\) is an equation of a straight line with slope equal to \(3\).

Exercise \(\PageIndex{52}\)

52. In the triangle given  \(\sin \alpha =\displaystyle \frac{a}{c}\)

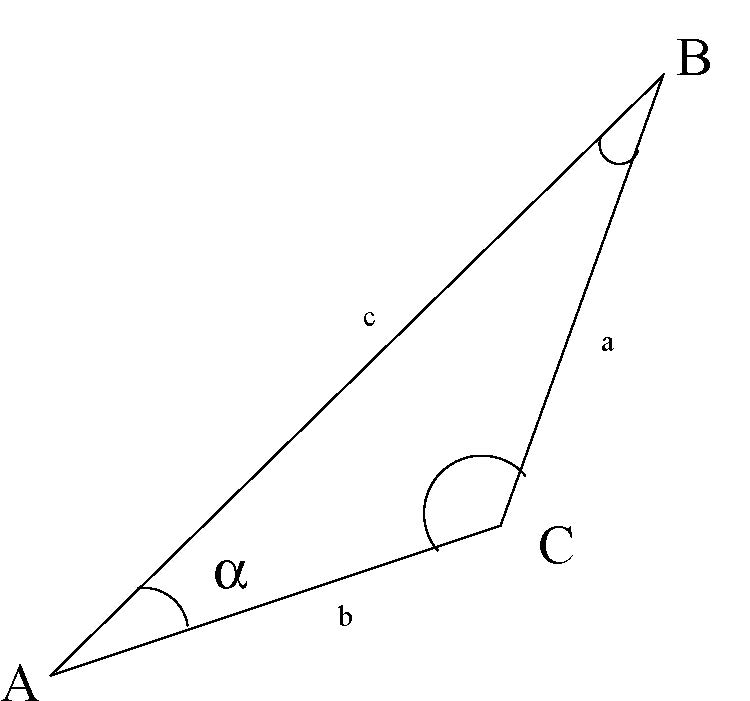
Answer

False. \(\sin \alpha\) is defined for right angled triangles.

Exercise \(\PageIndex{53}\)

53. The area of the triangle is \(1/2 ab.\)

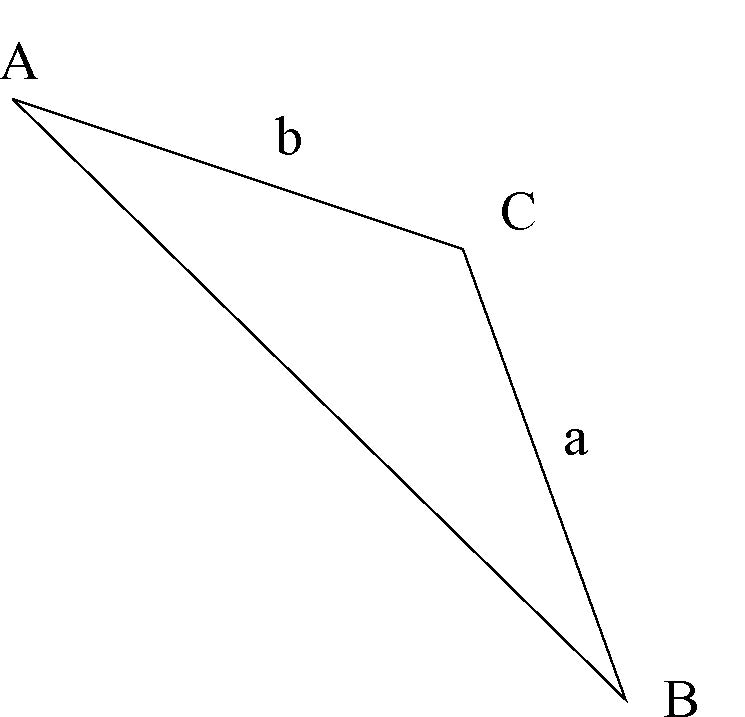
Answer

False. The area of a triangle is \(\displaystyle{\displaystyle \frac{1}{2} bh}\), where \(b\) is the base and \(h\) is the height of the triangle. 

Exercise \(\PageIndex{54}\)

54. Two triangles are said to be similar if and only if they have the same area.

Answer

False. Two triangles are said to be similar if and only if their angles are equal. 

Exercise \(\PageIndex{55}\)

55. Two triangles are said to be similar if and only if they have sides of the same length.

Answer

False. See question above. 

Exercise \(\PageIndex{56}\)

56. Two triangles are said to be similar if and only if their angles are equal.

Answer

True. 

Exercise \(\PageIndex{57}\)

57. An isoceles triangle is a triangle in which all the sides have the same length.

Answer

False. An isosceles triangle is a triangle in which two sides have the same length. 

Exercise \(\PageIndex{58}\)

58. An equilateral triangle must also be right angled.

Answer

False. The angles of equilateral triangle are all \(60^{\circ}\). 

Exercise \(\PageIndex{59}\)

59. The centre of the circle \((x-1)^2+(y+3)^2=5\) is \(c=(-1,3).\)

Answer

False. The centre of the circle is \((1,-3)\). 

Exercise \(\PageIndex{60}\)

60. To solve the inequality, $$\displaystyle \frac{x-1}{x} >0,$$ we proceed as follows:

Multiply both sides by \(x\) to get \(x-1>0 \Rightarrow x>1\) .

Answer

False. To solve use a sign chart. The process described does not work because we don't know if \(x\) is positive or negative. If \(x\) is negative, then multiplication by \(x\) causes a change in the inequality.

Exercise \(\PageIndex{61}\)

61. \( \sin{\pi}=180^{\circ}\)

Answer

False. \(\sin (\pi) = 0\)

Exercise \(\PageIndex{62}\)

62. If \(x=1\) then \(\sin x=\sin 1=0.17452406\).

Answer

False. \(\sin (1) = 0.841470985\)

Exercise \(\PageIndex{63}\)

63. If \( \sin x= \displaystyle \frac{1}{2}\) then \( \sin x= 30^{\circ}\).

Answer

True. 

Exercise \(\PageIndex{64}\)

64. \(\cos(-x)= \cos x\)

Answer

False. \(\cos (-x) = \cos (x)\)

Exercise \(\PageIndex{65}\)

65. On the number line shown below, the collection of real numbers represented is \([ - \infty,2).\)

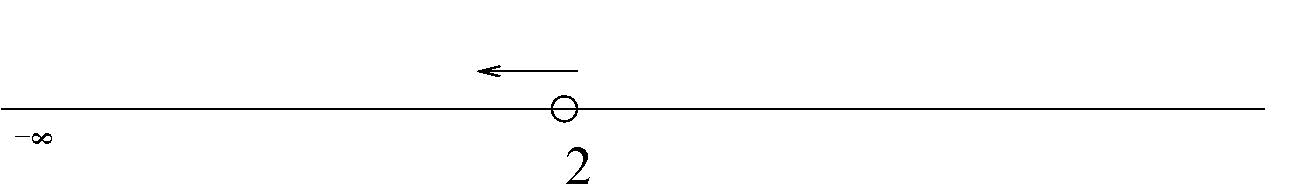
Answer

False. The collection is \((-\infty, 2)\). 

Exercise \(\PageIndex{66}\)

66. On the number line shown above, the collection of real numbers represented is \((2, - \infty).\)

Answer

False. See question above.

Exercise \(\PageIndex{67}\)

67. The interval \((-5,4]\) can be represented on the real number line as shown below.

Answer

False. The interval is \([-5,4)\).

Exercise \(\PageIndex{68}\)

68. \( \sqrt[4]{x^3}=x^{4/3}\)

Answer

False. \(\sqrt[4]{x^3} = x^{3/4}\)

Exercise \(\PageIndex{69}\)

69. \(\sqrt{64}= \pm 8\)

Answer

False. \(\sqrt{64} = 8\)

Exercise \(\PageIndex{70}\)

70. \(\sqrt{-1}= -1\)

Answer

False. \(\sqrt{-1} = i\)

Exercise \(\PageIndex{71}\)

71. \(\sqrt[3]{x^2}= x^{2/3}\)

Answer

True.

Exercise \(\PageIndex{72}\)

72. The pair of straight lines \(2x+y-1=0\) and \(2y+x-1=0\) are parallel.

Answer

False. The lines are neither parallel nor perpendicular. 

Exercise \(\PageIndex{73}\)

73. The point of intersection of the parallel lines \( 3x+2y-1=0,\) and \(6x+4y+17=0\) is \((-1,4).\)

Answer

False. There is no point of intersection of parallel lines. 

Exercise \(\PageIndex{74}\)

74. The graphs of \(y=-2\) and \(x=5\) are as shown below.

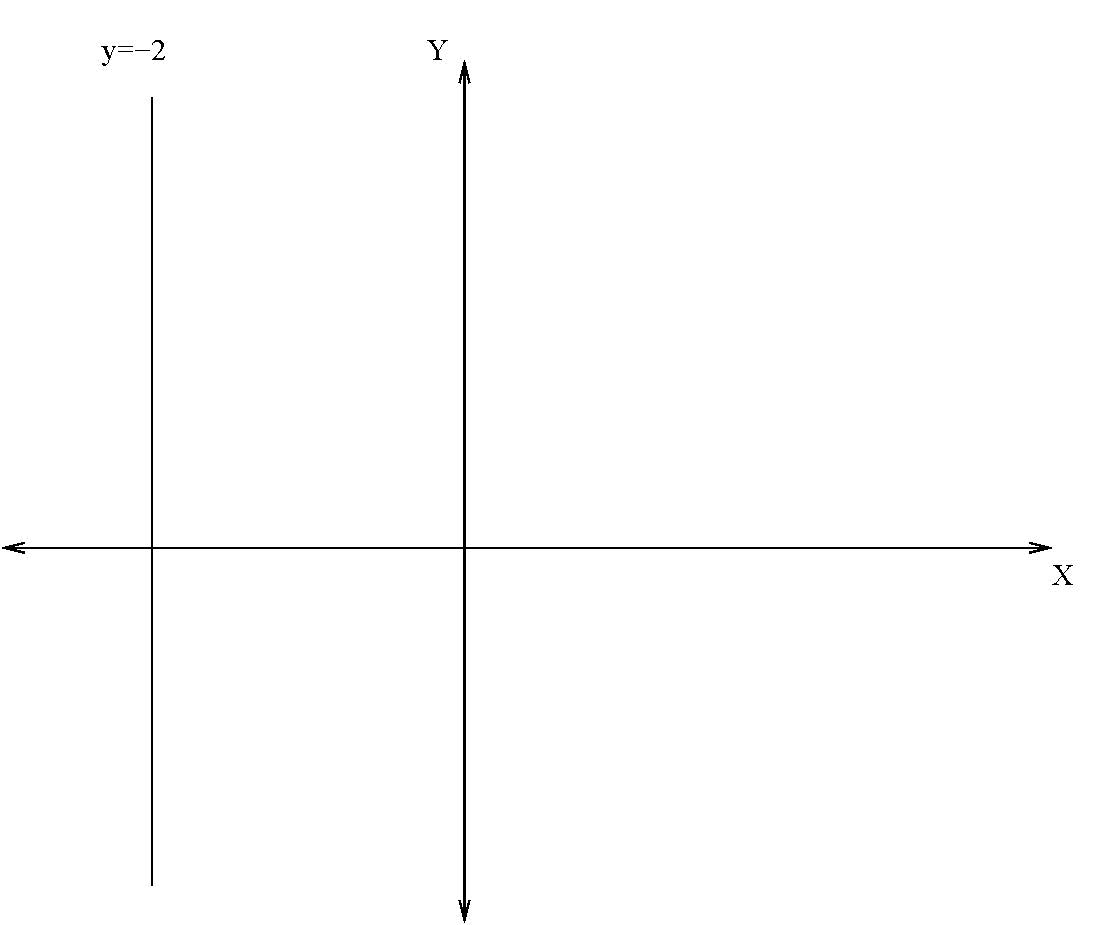
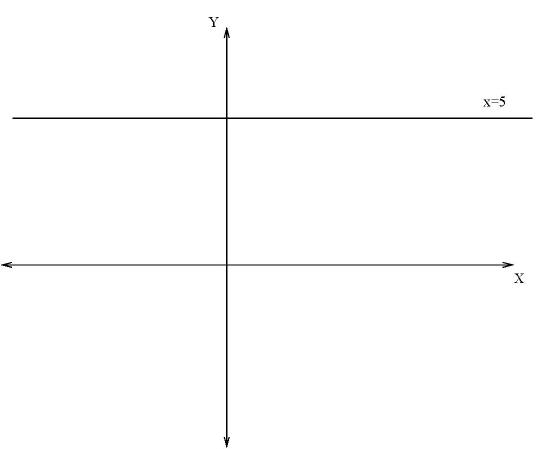
Answer

False. The graphs of \(x = -2\) and \(y = 5\) are shown. 

Exercise \(\PageIndex{75}\)

75. The straight line \(2x+3y=12\) has an \(x-\)intercept of \(6\) and \(y-\)intercept of \(4.\) Therefore, the line must contain the point \((6,4).\)

Answer

False. The intercepts are correct but the line would contain the points \((6,0)\) and \((0,4)\). 

Exercise \(\PageIndex{76}\)

76. If \(\sin x= \displaystyle \frac{3}{5},\) then \(\sec x= \displaystyle \frac{5}{3}.\) 

Answer

False. If \(\sin (x) = 3/5\), then \(\csc (x) = 5/3\).

Exercise \(\PageIndex{77}\)

77. \(|x^2|=-x^2\) if \(x<0.\)

Answer

False. \(|x^2| = x^2\) for all \(x\). 

Exercise \(\PageIndex{78}\)

78. \(|-x|=x\) if \(x<0.\)

Answer

False. \(|-x| = x\) if \(x>0\).

Exercise \(\PageIndex{79}\)

79. \(|-3x|=-3x\) if \(x<0.\)

Answer

True.

Exercise \(\PageIndex{80}\)

80. \(x^2y=xy^2.\)

Answer

False. There is no way of fixing this.

Exercise \(\PageIndex{81}\)

81. \(\sqrt[3]{-x}\) is not defined for any real number values of \(x.\)

Answer

False. \(\sqrt[3]{-x}\) is defined for all real numbers. 

Exercise \(\PageIndex{82}\)

82. If \(x^3=2,\) then \(x=2^3=8.\)

Answer

False. If \(x^3 = 2\), then \(x = \sqrt[3]{2}\).

Exercise \(\PageIndex{83}\)

83. If \(\sqrt[3]{x}=8,\) then \(x=\sqrt[3]{8}=2.\)

Answer

False. If \(\sqrt[3]{x} = 8\), then \(x = 8^3=512\).

Exercise \(\PageIndex{84}\)

84. The equation \(\sqrt[3]{x}=-1\) has no real number solutions.

Answer

False. The solution is \(x = -1\). 

Exercise \(\PageIndex{85}\)

85. The graph of \(y= \cos x\) is the one shown below:

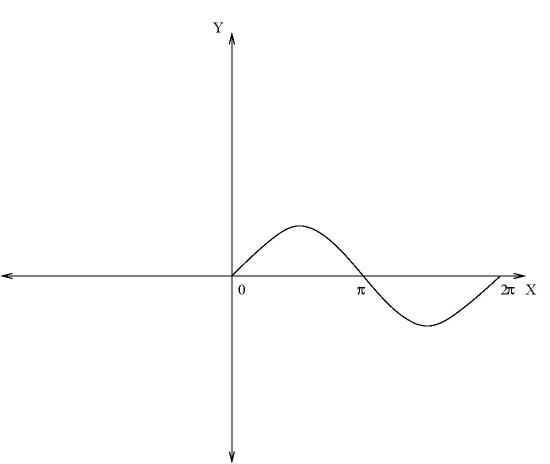
Answer

False. The graph of \(y = \sin (x)\) is shown. 

Exercise \(\PageIndex{86}\)

86. The inequality \(-1 \leq x \geq 2\) is valid.

Answer

True. It is redundant as it is equivalent to \(x \geq -1\). 

Exercise \(\PageIndex{87}\)

87. The inequality \(-1 \geq x \geq 2\) is valid.

Answer

True. 

Exercise \(\PageIndex{88}\)

88. The radius of the circle \(4x^2+4y^2=81\) is equal to \(9\) units.

Answer

False. The radius is \(9/2\). 

Exercise \(\PageIndex{89}\)

89. Every pair of straight lines is either parallel or perpendicular.

Answer

False. For example, \(y = x\) and \(y = 2x\) are neither parallel nor perpendicular.

Exercise \(\PageIndex{90}\)

90. The equation of the \(x-\)axis is \(x=0.\)

Answer

False. The equation of the \(x-\)axis is \(y=0\). 

Exercise \(\PageIndex{91}\)

91. The equation of the \(y-\)axis is \(x=0.\)

Answer

True. 

Exercise \(\PageIndex{92}\)

92. \(x^2+1=(x+1)(x+1).\)

Answer

False. \(x^2+1\) is not factorable. 

Exercise \(\PageIndex{93}\)

93. \(x^3+1=(x^2+1)(x+1).\)

Answer

False. \(x^3+1 = (x+1)(x^2-x+1)\)

Exercise \(\PageIndex{94}\)

94. \(x^4-1=(x-1)(x-1)(x-1)(x-1).\)

Answer

False. \(x^4-1 = (x-1)(x+1)(x^2+1)\)

Exercise \(\PageIndex{95}\)

95. The slope of the straight line \(3y=5x-2\) is \(5.\)

Answer

False. The slope is \(5/3\). 

Exercise \(\PageIndex{96}\)

96. The distance between the points \((0,0)\) and \((5,5)\) is \(5\) units.

Answer

False. The distance is \(5\sqrt{2}\) units.

Exercise \(\PageIndex{97}\)

97. The distance between the points \((-5,0)\) and \((5,5)\) is \(0\) units.

Answer

False. The distance is \(10\) units.

Exercise \(\PageIndex{98}\)

98. The point-slope formula for the equation of a straight line may be expressed as \( x-x_1=m(y-y_1)\) where \(m\) is the slope of the straight line and the line contains the point \((x_1,y_1).\)

Answer

False. The equation is \(y-y_1 - m(x-x_1)\).

Exercise \(\PageIndex{99}\)

99. \(x^2-10x-24=(x-4)(x-6)\)

Answer

False. \(x^2-10x+24 = (x-4)(x-6)\)

Exercise \(\PageIndex{100}\)

100. \(x^2-10x+24=(x-12)(x+2)\)

Answer

False. \(x^2-10x-24 = (x-12)(x+2)\)

Exercise \(\PageIndex{101}\)

101. If \(ax^2+bx+c=0\) then

a. \( \displaystyle x=\displaystyle \frac {\pm \sqrt{(b^2-4ac)}}{2a}\)

b. \( \displaystyle x=\displaystyle \frac {-b \pm \sqrt{(4ac-b^2)}}{2a}\)

Answer

Both are false. \(\displaystyle{x = \displaystyle \frac{-b\pm\sqrt{b^2-4ac}}{2a}}\)

Exercise \(\PageIndex{102}\)

102. Question: Simplify \(\displaystyle \frac{x+1}{x-1}=\frac{x+2}{x-4}\)

Answer: by cross multiplying we get,

\begin{eqnarray*}
(x+1)(x-4) &=& (x+2)(x-1)\\
\Rightarrow x^2-3x-4 &=& x^2+x-2\\
\Rightarrow -4x &=& 2\\
\Rightarrow  x=\displaystyle \frac{-1}{2}
\end{eqnarray*}

Answer

False. We are asked to simplify an expression not an equation. Therefore are solution should be a fraction and not \(x =\) something. The answer is obtained by making the expression into a single expression: \(\displaystyle{\displaystyle \frac{(x+1)(x+2)}{(x-1)(x-4)}}\).

Exercise \(\PageIndex{103}\)

103. If \(\displaystyle \frac{x+1}{x-1}=0\) then \((x-1)=0(x^2+3)\Rightarrow x-1=x^2+3\) 

Answer

False. If we have \(x-1 = 0 \cdot (x^2+3)\), then \(x-1 = 0\). 

Exercise \(\PageIndex{104}\)

104. If \(\log_2x=5\) then one of the following is true:

a. \(x=5^2\)

b. \(x^2=5\)

c. \(5^x=2\)

d. \(x=2^5\)

e. \(2^x=5\)

f. None of the above.

Answer

d. is true. 

Exercise \(\PageIndex{105}\)

105. If \(f(x)=\displaystyle \frac{x^2-4}{x-2}\) then \(f(2)=\displaystyle \frac{4-4}{2-2}=\displaystyle \frac{0}{0}=1.\)

Answer

False. \(f(2)\) is undefined because of division by zero. 

Exercise \(\PageIndex{106}\)

106. \(\displaystyle \frac{2}{x}+\displaystyle \frac{5}{y}=\displaystyle \frac{2y+5x}{x+y}\)

Answer

True.

Exercise \(\PageIndex{107}\)

107. To sketch a straight line, you need at least three points which lie on the straight line.

Answer

False. To sketch a straight line you need two points. 

Exercise \(\PageIndex{108}\)

108. A circle is completely determined if its centre and radius are known.

Answer

True.

Exercise \(\PageIndex{109}\)

109. \( \sqrt{-x}\) is undefined because of the negative sign.

Answer

False. \(\sqrt{-x}\) is defined if \(x<0\). 

Exercise \(\PageIndex{110}\)

110. \(\log (xy)= (\log x) (\log y)\)

Answer

False. \(\log(xy) = \log (x) + \log (y)\)

Exercise \(\PageIndex{111}\)

111. \(3^0=0\)

Answer

False. \(3^0 = 1\)