0.1: Sets

Sets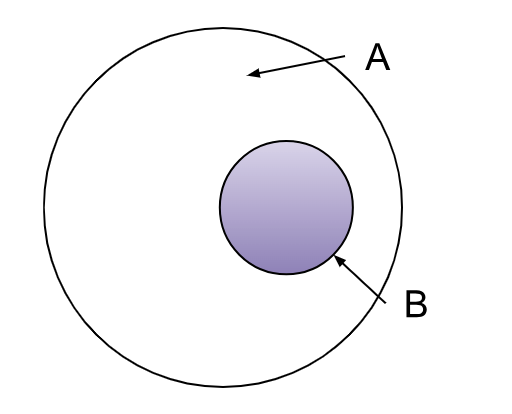

• Sets are collections of objects,

• Sets are normally denoted by capital letters.

• Elements are denoted by lower-case letters.

• Subsets:  

  • Every element of B is an element of A, written as $B\subset A.$

  • $B=\{a \in A:$ …..condition on okay!. 

  • Trivial subsets of $A$ are $A$ and $\emptyset$ (empty set).

• How do we test if an element belongs to a set?

Example $\PageIndex{1}$

$M_{22}(\mathbb{R}):=$ set of all 2 x 2 matrices with real numbers, where $\mathbb{R}:=$ set of all real numbers.

Let  $A=\big{\{}\begin{bmatrix}x\end{bmatrix} \in M_{22}(\mathbb{R})|\begin{bmatrix}x\end{bmatrix}\begin{bmatrix}1 &1\\ 0 &1\end{bmatrix}=\begin{bmatrix}1 &1\\ 0 &1\end{bmatrix}\begin{bmatrix}x\end{bmatrix}\big{\}}$.

 

Determine whether the following entries belong to $A$.

 

1. $\begin{bmatrix}1 & 0\\ 0 & 0\end{bmatrix}$ does not belong to $A$.

Answer

$\begin{bmatrix}1 & 0\\ 0 & 0\end{bmatrix} \cdot \begin{bmatrix}1 &1\\ 0 &1\end{bmatrix}=\begin{bmatrix}1 &1\\ 0 &0\end{bmatrix}$ and

$\begin{bmatrix}1 &1\\ 0 &1\end{bmatrix} \cdot \begin{bmatrix}1 & 0\\ 0 & 0\end{bmatrix}=\begin{bmatrix}1 &0\\ 0 &0\end{bmatrix}$

Since $\begin{bmatrix}1 &1\\ 0 &0\end{bmatrix} \ne \begin{bmatrix}1 &0\\ 0 &0\end{bmatrix}$, $\begin{bmatrix}1 & 0\\ 0 & 0\end{bmatrix} \notin A$.◻

 

2. $\begin{bmatrix}0 & 1\\ 0 & 0\end{bmatrix}$ does belong to $A$.

Answer

$\begin{bmatrix}0 & 1\\ 0 & 0\end{bmatrix} \cdot \begin{bmatrix}1 &1\\ 0 &1\end{bmatrix}=\begin{bmatrix}0 &1 0 &0\end{bmatrix}$

$\begin{bmatrix}1 &1\\ 0 &1\end{bmatrix} \cdot \begin{bmatrix}0 & 1\\ 0 & 0\end{bmatrix}=\begin{bmatrix}0 &1\\ 0 &0\end{bmatrix}$

Since $\begin{bmatrix}0 &1\\ 0 &0\end{bmatrix} = \begin{bmatrix}0 &1\\ 0 &0\end{bmatrix}$, $\begin{bmatrix}1 & 0\\ 0 & 0\end{bmatrix} \in A$.◻

3. $\begin{bmatrix}0 & 0\\ 1 & 0\end{bmatrix}$ does not belong to $A$.

Answer

$\begin{bmatrix}0 & 0\\ 1 & 0\end{bmatrix} \cdot \begin{bmatrix}1 &1\\ 0 &1\end{bmatrix}=\begin{bmatrix}0 &0\\ 1 &1\end{bmatrix}$

$\begin{bmatrix}1 &1\\ 0 &1\end{bmatrix} \cdot \begin{bmatrix}0 & 0\\ 1 & 0\end{bmatrix}=\begin{bmatrix}1 &0\\ 1 &0\end{bmatrix}$

Since $\begin{bmatrix}0 &0\\ 1 &1\end{bmatrix} \ne \begin{bmatrix}1 &0\\ 1 &0\end{bmatrix}$, $\begin{bmatrix}0 & 0\\ 1 & 0\end{bmatrix} \notin A$.◻

4. $\begin{bmatrix}0 & 0\\ 0 & 1\end{bmatrix}$ does not belong to $A$.

Answer

$\begin{bmatrix}0 & 0\\ 0 & 1\end{bmatrix} \cdot \begin{bmatrix}1 &1\\ 0 &1\end{bmatrix}=\begin{bmatrix}0 &0\\ 0 &1\end{bmatrix}$

$\begin{bmatrix}1 &1\\ 0 &1\end{bmatrix} \cdot \begin{bmatrix}0 & 0\\ 0 & 1\end{bmatrix}=\begin{bmatrix}0 &1\\ 0 &1\end{bmatrix}$

Since $\begin{bmatrix}0 &0\\ 0 &1\end{bmatrix} \ne \begin{bmatrix}0 &1\\ 0 &1\end{bmatrix}$, $\begin{bmatrix}0 & 0\\ 0 & 1\end{bmatrix} \notin A$.◻

5. $\begin{bmatrix}0 & 0\\ 0 & 0\end{bmatrix}$.  does belong to $A$.

Solution

This one is obviously true, thus $\begin{bmatrix}0 & 0\\ 0 & 0\end{bmatrix} \in A$.

Notations:

• $\cup$ or / union

• $\cap$ and / intersection

• $\{\}^c$ complement of a set (aka $\{\}^{'}$).

• $A \backslash B$ is equivalent to $A \cap B^{'}$.

• $\mathbb{Z}:=$ set of all integers $=\{\ldots,-2,-1,0,1,2,\ldots\}$.  A countable set.

• $\mathbb{Q}:=$ set of all rational numbers $=\{\frac{a}{b}: a,b \in \mathbb{Z}, b \ne 0 \}$.   A countable set.

• $\mathbb{Q}^c:=$  set of all irrational numbers $=\{\pm e, \pm \pi, \pm \sqrt{2}, \ldots\}$.   Not a countable set.

• $\mathbb{R}:=$ set of all real numbers $=\mathbb{Q} \cup \mathbb{Q}^c$.  Note $\mathbb{Q} \cap \mathbb{Q}^c=\emptyset$.  Not a countable set.

• $\mathbb{C}:=$ set of all complex numbers.

• $M_{mn}(\mathbb{R}):=$ set of all $m \times n$ matrices over real numbers.

• $M_{mn}(\mathbb{C}):=$ set of all $m \times n$ matrices over complex numbers.

• The cardinality of a set $A$ is written as $|A|$.



•  

Example $\PageIndex{2}$

$\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} \subseteq \mathbb{R} \subseteq \mathbb{C}$.

Example $\PageIndex{3}$

Let $A=\{1,2,3,5\}$.  Therefore $|A|=4$. In this case, $A$ is called a finite set.