4.3 : Homomorphisms

Last updated
Save as PDF

Page ID: 132495

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Definition: Homomorphism

Let $(G_1,\star_1)$, $(G_2, \star_2)$ be groups.

Then a function $h:G_1 \rightarrow G_2$ s.t. $h(g_1)=g_2, g_1 \in G_1 \text{and } g_2 \in G_2$ is called a homomorphism from the group $G_1$ to the group $G_2$ if $h(g_1 \star_1g_1^{\shortmid})=h(g_1)\star_2 h(g_1^{\shortmid}), \;g_1,g_1^{\shortmid} \in G_1$.

Further, if $h$ is a bijection and also a homomorphism, then $h$ is called an isomorphism. In this case, we say $G_1 \cong G_2$, which means that $G_1$ is congruent to $G_2$.

Example $\PageIndex{1}$

Let $C_n=<a,a^n=e>$ be a cyclic group.

Define: $h: C_n \rightarrow \mathbb{Z}_n $ by $h(a^k)=k \pmod{n}$. Then

Is $h$ a homomorphism?
Is $h$ injective (1-1)?
Is $h$ surjective (onto)?

If all three are true, then $h$ is an isomorphism.

Proof:

We will show a finite cyclic group is always isomorphic to $(\mathbb{Z}_n, + \pmod{n})$.

Proof of Homomorphism:

Let $g_1,g_2 \in C_n$.

We shall show that $h(g_1\star_1 g_2)=h(g_1)\star_2h(g_2)$.

Consider $g_1=a^{k_1}$ and $g_2=a^{k_2}$.

Then $h(g_1)=k_1 \pmod{n}$ and $h(g_2)=k_2 \pmod{n}$.

$g_1\star_1 g_2=a^{k_1} \star_1 a^{k_2}=a^{k_1+k_2}$.

Thus $h(g_1\star_1g_2)=k_1+k_2 \pmod{n}$.

Now consider $h(g_1)\star_2 h(g_2)=k_1 \pmod{n} +k_2 \pmod{n}$

$=k_1+k_2 \pmod{n}$.

Hence $h(g_1\star_1 g_2)=h(g_1)\star_2h(g_2)$.

Hence $h$ is a homomorphism.◻

Proof of Injection (1-1):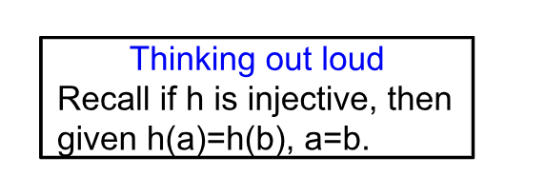 $Screen Shot 2023-07-06 at 4.34.19 PM.png$

Let $g_1, g_2 \in G$ s.t. $h(g_1)=h(g_2)$.

Since $g_1, g_2 \in C_n$, $g_1=a^{k_1}$ and $g_2=a^{k_2}, \; k_1,k_2 \in \mathbb{Z}$.

Now, $h(g_1)=k_1 \pmod{n}=k_2 \pmod{n}=h(g_2)$.
Therefore, $k_1=k_2 \in \mathbb{Z}_n$.

Hence $h$ is injective (1-1).◻

Proof of Surjective (onto):

Let $k \in \mathbb{Z}_n$. $Screen Shot 2023-07-06 at 4.35.09 PM.png$

Since $a^k \in C_n$ by definition $h(a^k)=k \pmod{n}$.

Hence $h$ is surjective.◻

Since a finite cyclic group is homomorphic, injective and surjective to $(\mathbb{Z}_n, + \pmod{n})$, it is isomorphic to $(\mathbb{Z}_n, + \pmod{n})$. ◻

Example $\PageIndex{2}$

Define $ h: (\mathbb{Z}, +) \to ( \mathbb{Z}_n, \cdot (mod n) $ defined by

$ h(k)= a^k, $ where $ \mathbb{Z}_n = <a>, k \in \mathbb{Z}. $ Then

For $ k, m \in \mathbb{Z}, h(k+m)= a^{k+m}= a^k a^m= h(k)h(m). $ Thus $h$ is a homomorphism.

Notice that

$ 0 $

$ \pm n $

$ \pm 2n $

$ \pm 3n $

$ 1 $

$ 1 \pm n $

$ 1 \pm 2n $

$ 1 \pm 3n $

$ \cdots$

$ n-1 $

$n-1 \pm n $

$ n-1 \pm 2n $

$ n-1 \pm 3n $

$\mathbb{Z} $

$ \downarrow$

$ a^0$

$a^1$

$a^{n-1}$

$\mathbb{Z}_n $

Hence $ h $ is onto but not one to one.

Properties of homomorphisms:

Theorem $\PageIndex{1}$

Let $h: G_1 \rightarrow G_2$ be a homomorphism. Then:

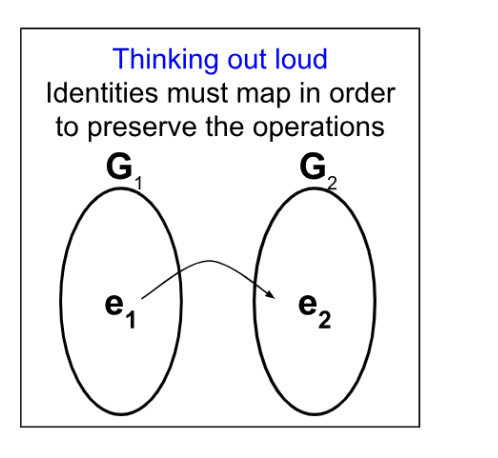
$ h(e_1)=e_2 $, where $ e_1, e_2 $ are identities of $ G_1, G_2 $ respectively. $Screen Shot 2023-07-06 at 4.39.50 PM.png$
$h(g_1^{-1})=h(g_1)^{-1}, g_1 \in G_1$.
$h(g^n)=h(g)^n$, $ n \in \mathbb{Z} $

Proof:

Since $ e_1 $ is the identity of $ G_1 $, $ e_1 e_1=e_1. $

Since $ h $ is a homomorphism, $ h(e_1e_1)= h(e_1) h(e_1)=h(e_1)=e_2 h(e_1). $

By cancellation law, $e_2 = h(e_1). $

Let $ g_1 \in G_1.$ Then $ g_1g_1^{-1}=e_1.$

Since $ h $ is a homomorphism, $ h(g_1g_1^{-1})=h(g_1) h(g_1^{-1}) = h(e_1)=e_2.$

Hence $ (h(g_1))^{-1} = h(g_1^{-1}). $

Use induction on $ \mathbb{Z}_+ $.

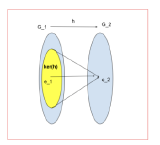
$Screen Shot 2023-07-06 at 4.41.46 PM.png$ Definition:

Let $ h: G_1 \to G_2$ be a homomorphism. Then

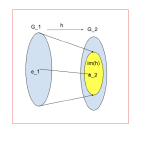
$Screen Shot 2023-07-06 at 4.43.00 PM.png$ The kernel of $h$ is defined as $ ker(h)=\{g_1 \in G_1| h(g_1)=e_2 \}. $
The image of $h$ is defined as $ im(h)= \{ g_2 \in G_2| h(g_1)=g_2, g_1 \in G_1\}.$

Theorem $\PageIndex{1}$

Let $ h: G_1 \to G_2$ be a homomorphism. Then $ ker(h) \leq G_1 $ and $ im(h) \leq G_2. $ Also, $\ker (h) $ is a normal subgroup of $G _1$.

Proof:

Let $ h: G_1 \to G_2$ be a homomorphism.

Since $ h(e_1)=e_2, e_1 \in ker(h).$ Let $ g_1, g_1^{'} \in ker(h).$ Then $ h(g_1)=e_2 $ and $ h( g_1^{'}) =e_2. $

Similarly, we can show that $ im(h) \leq G_2. $

We shall show that $ g_1^{-1} g_1^{'} \in ker(h).$

Consider $ h(g_1^{-1} g_1^{'})= h(g_1^{-1})h( g_1^{'}) = h(g_1)^{-1} h( g_1^{'}) = e_2^{-1} e_2=e_2. $ Hence $ g_1^{-1} g_1^{'} \in ker(h).$ Thus $ ker(h) \leq G_1. $

We shall show that $\ker (h) $ is a normal subgroup of $G_1 $.

Let $h \in \ker(h) $ s.t. $h(h)=e_H $.

We will show $ghg^{-1}\in \ker(h), \forall \; g \in G_1 $.

Consider $h(ghg^{-1})=h(g) h(h) h(g^{-1}) $

$= h(g) h(h) (h(g))^{-1} $

$=h(g) e_H (h(g))^{-1} $

$=h(g) (h(g))^{-1} $

$=e_H $.

So $\ker(h) $ is a normal subgroup of $G_1 $.

Definition: Homomorphism

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Theorem \(\PageIndex{1}\)

Definition:

Theorem \(\PageIndex{1}\)

$Screen Shot 2023-07-06 at 4.41.46 PM.png$ Definition: