6.1: Introduction to Rings
- Page ID
- 132508
Recall a group is a set with a binary operation; rings are algebraic structures similar to groups but with two operations instead of one.
A non-empty set \(R\) with two binary operations, addition and multiplication - denoted by \(+\) and \(\bullet\), is called a ring if:
-
\((R,+)\) is an abelian group .
-
\(a(bc)=(ab)c, \; \forall a,b,c \in R\). \(R\) in this context is a ring. Note \((R,\bullet)\) is a semigroup.
-
\(a \bullet (b+c)=ab+ac\) and \((b+c)a=ba+ca\), \(\forall a,b,c \in R\). Distributive property.
A ring \((R, +, \bullet)\) is called a commutative ring if \(ab=ba, \; \forall a,b \in R\).
A ring \((R, +, \bullet)\) has a unity(identity) \(e \in R\) if \(ae=ea=a, \; \forall a \in R\). Note unity is always a unique, single element.
An element \(a\in R\) is called a unit if there exists an \(a^{-1}\in R\) s.t. \(aa^{-1}=e\).
- \((\mathbb{Z},+, \bullet)\) is a commutative ring with unity \(1\), and each \( a \in \mathbb{Z} \setminus \{0\}\) is a unit.
-
\((\mathbb{Z}_n,\bigoplus, \bigodot)\) (modulo n addition and multiplication) is a commutative ring with unity 1 and units of \(U(n)\) since they must be all the elements relatively prime to n.
-
\((\mathbb{Z}_{[x]}, +, \bullet)\) where \(\mathbb{Z}_{[x]}\) is the set of all integer polynomials in variable \(x\), is a commutative ring with unity of 1 and units of \(\pm 1\).
-
\((M_{22}(\mathbb{Z}), +, \bullet)\) is a ring, from the set of all \(2 \times 2\) matrices with integer entries, that has unity \(I\). It is a non-commutative ring. The units are the set of all \(2 \times 2\) matrices with a non zero determinant \((GL_2(\mathbb{R}))\).
-
\((\mathbb{R},+, \bullet)\) is called a field. It is a commutative ring, and inverses exist for all elements except 0.
-
\((\mathbb{C},+, \bullet)\) is also a field, and inverses exist for all elements except 0.
-
A polynomial ring \(R[x]\) over a ring \(R\) is defined as \(\{(p(x)=a_0+a_1x+\cdots+a_nx^n| n \in \mathbb{Z}, n\geq 0, a_i \in R, \forall i=1, \cdots, n\}\). Where \(a_i\) is the coefficient of \(x^i\), also called the coefficients of the polynomial, and the non-negative integer \(n\) is called the degree of the polynomial.
The coefficients \(a_i\) can be elements from any ring, such as integers, rational numbers, real numbers, complex numbers, or even other polynomials. The addition and multiplication of \( R[x] \) are the addition and multiplication \(R.\)
Integral Domain (ID)
Recall: \((R,+,\bullet)\) is a non-empty set with closed binary operations.
\((R,+)\) is abelian.
\((R,\bullet)\) is a semigroup. Recall this is a set with an associative operation, no identity.
\((R,+,\bullet)\) is distributive, has unity (aka identity) of 1 and unit of \(aa^{-1}=e\)
If \(ab=ba\), the ring is commutative on \(\bullet\).
A commutative ring with unity (aka identity), \(R\), is called an integral domain if for every \(a,b \in R\), \(ab=0\) implies \(a=0\) or \(b=0\).
An example of a non-integral domain is
\(\begin{bmatrix} 1 & 0 \\0 & 0 \end{bmatrix} \begin{bmatrix} 0 & 0 \\0 & 1 \end{bmatrix}=\begin{bmatrix} 0 & 0 \\0 & 0 \end{bmatrix}\), but neither \(\begin{bmatrix} 1 & 0 \\0 & 0 \end{bmatrix}\) nor \( \begin{bmatrix} 0 & 0 \\0 & 1 \end{bmatrix}\) equal zero.
A division ring is a ring, (R), with an identity in which for every non-zero \(a \in R\), there exists \( b \in R\) s.t. \(ab=1=ba\).
A field is a commutative division ring.
Examples of fields are: \((\mathbb{Q},+,\bullet)\), \((\mathbb{R},+,\bullet)\), and \((\mathbb{C},+,\bullet)\), with the later being algebraically closed.
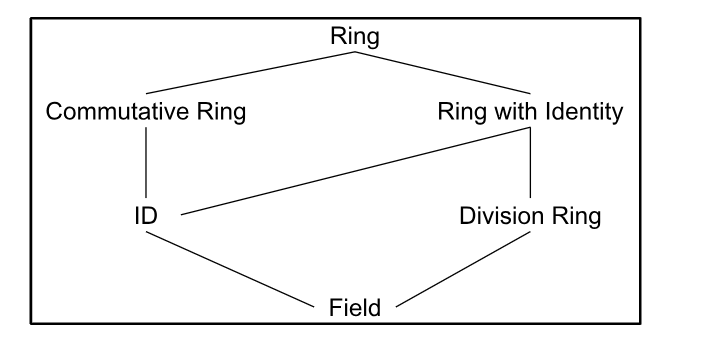
A non-zero element of \(a \in R\) is called a zero divisor if there exists \(ab \in R\) s.t. \(ab=0\).
\((\mathbb{Z},+,\bullet)\).
Since there are no zero divisors, it is an integral domain. It is a commutative ring. Since zero does not have an inverse, not every element has an inverse. Thus, it is not a field.
\((\mathbb{Z}_n,\oplus,\odot)\).
There are two cases.
This is a finite field if \(n\) is prime.
If \(n\) is not prime, then it is not an integral domain since it will have a zero divisor.
The set of all real-valued differentiable functions on \([a,b]\) is a commutative ring with a unit. This area of study is called differential algebra.
\(M_{22}(\mathbb{R},+,\bullet))\).
The addition is abelian. It is not commutative. It has an identity. Not an integral domain.
This area of study is called matrix algebra.
Let
\(1=\begin{bmatrix} 1 & 0 \\0 & 1 \end{bmatrix}, I= \begin{bmatrix} 0 & 1 \\-1 & 0 \end{bmatrix}, J= \begin{bmatrix} 0 & i \\i & 0 \end{bmatrix}, K= \begin{bmatrix} i & 0 \\0 & -i \end{bmatrix} \).
Define
\( R= \{ a+bI+cJ+dK |a,b,c,d \in \mathbb{R} \}.\) Then \( R \) is Ring of Quaternions.
Let
\( \mathbb{H}= \left \{ \begin{bmatrix} a & b \\- \bar{b} & \bar{a} \end{bmatrix} | a, b \in \mathbb{C} \right\}.\)
Then \( \mathbb{H} \) is a division ring with matrix addition and multiplication, but not an integral domain.
Properties of Rings
 Let \(D\) be a commutative ring with identity. Then \(D\) is an integral domain if and only if \(ab=bc\) implies \(b=c\; \forall a,b,c \in D\).
Let \(D\) be a commutative ring with identity. Then \(D\) is an integral domain if and only if \(ab=bc\) implies \(b=c\; \forall a,b,c \in D\).
Let \((R,+, \bullet)\) be a ring and \(a,b \in R\).
-
\(a0=0=0a\).
-
\(a(-b)=(-a)b=-ab\).
-
\((-a)(-b)=(ab)\).
- Answer
-
1. Let \( a \in R. \) Then \( 0 a=(0+0) a=0a+0a. \implies 0a+0=0a+0a.\) By cancellation law of \( + \), we get \( 0a=0. \) Similarly, we can show that \( a 0=0. \)
2. Let \( a, b \in R. \) Then \( ab+(-a)b=(a+(-a))b=0 b=0. \implies (-a)b=-(ab).\) Similarly, \( ab+a(-b)=a(b+(-b))=a 0=0. \implies a(-b)=-(ab).\)
Subring:
Let \((R,+,\bullet)\) be a ring.
Let \(S(\ne 0) \subseteq R\).
Then \(S\) is a subring of \(R\) if \((S,+,\bullet)\) is a ring with the same operations.
Subring Test
Let \((R,+,\bullet)\) be a ring.
\(S \subseteq R\) is a subring if and only if the following conditions are satisfied:
-
\(S \ne \{\}\). At least \(0\in S\).
-
\(a-b\in S\).
-
\(ab \in S, \; \forall a,b \in A\).
Let \((R,+,\bullet)\) be a ring then \(\{0\}\) and \(R\) are subrings of \(R\) and are called the trivial subrings of \(R\).
Let \((\mathbb{Q},+, \bullet)\) is a subring of \((\mathbb{R},+, \bullet)\) and \((\mathbb{R},+,\bullet)\) is a subring of \((\mathbb{C},+,\bullet)\).
\((\mathbb{Z}_6,\oplus, \odot)\) is a ring.
1. Let \( S=\{0, 3 \} \).
Clearly, \(S\) is non-empty.
Since \(0\oplus 3\), \(0 \oplus0\), and \(3 \oplus3\), \(a-b \in S\).
Since \(0\odot3\), \(0 \odot 0\), and \(3 \odot 3\), then \(ab \in S\) .
Thus \(S\) is a subring of \((\mathbb{Z}_6,\oplus, \odot)\).
2.
Let \( T =\{0, 2, 4 \} \).
Clearly, \(T\) is non-empty.
Since \(0 \oplus 0\), \(0 \oplus 2\), \(0 \oplus 4\), \(2 \oplus 2\),\(2 \oplus 4\) and \(4 \oplus 4\in T\) then \(a-b \in T\)
Since \(0 \odot 0\), \(0 \odot 2\), \(0 \odot 4\), \(2 \odot 2\), \(2 \odot 4\), and \(4 \odot 4 \in T\), then \(ab \in T\).
Thus \(T\) is a subring of \((\mathbb{Z}_6,\oplus, \odot)\).
Define \( \mathbb{Z}[i]=\{ m+ni|m.n \in \mathbb{Z}\}, \) where \( i^2=-1. \)
This is a ring called Gaussian integers. The units of this ring are \( \pm1\) and \( \pm i\). Hence The ring of Gaussian integers is not a field.This is a subring of \( (\mathbb{C},+,\cdot ). \)
Every finite integral domain is a field.
- Answer
-
Let \(D\) be a finite integral domain.
Let \(D^{*} = D \backslash \{0\}\).
We shall show that every element in \(D^*\) is a unit (i.e., \(aa^{-1}=e,\; \forall a \in D^*\)).
Let \(a\in D^*\).
Define \(\lambda_a : D^* \rightarrow D\) by \(\lambda_a(x)=ax, \; x\in D^*\).
We shall show that \(\lambda_a\) is injective.
Let \(x_1, x_2 \in D^*\) s.t. \(\lambda_a(x_1)=\lambda_a(x_2)\).
Consider \(ax_1=ax_2\).
Thus \(ax_1-ax_2=0\).
So \(a(x_1-x_2)=0\).
Since \(D\) is an integral domain, either \(a=0\) or \((x_1-x_2)\)=0\).\)
Since \(D^*\) excludes zero, \(a \ne 0\).

Thus \(x_1-x_2=0\).
Hence \(x_1=x_2\) and \(\lambda_a\) is injective.
Since \(D\) and \(D^*\) are finite, \(\lambda_a\) is surjective.
Since \(1 \in D^*, \; \exists x \in D^*\) s.t. \(\lambda_a(x)=1\).
Thus \(a\) is a unit, and therefore it is a field
Characteristic of a ring R
Let \( r \in R \), then \( r+r=2r, r+r+r=3r, \cdots, r+ \cdots+ r =nr.\)
The characteristic of a ring \( R\) is the least positive integer \( n \) such that \( nr=0, \forall r \in R. \) If no such \( n \) exists, we say that the characteristic of ring \(R\) is \( 0. \)
-
\( ( \mathbb{Z}, + \cdot), ( \mathbb{Q}, + \cdot), ( \mathbb{R}, + \cdot), ( \mathbb{C}, + \cdot) \) are rings of characteristic \( 0. \)
-
\((\mathbb{Z}_6,\oplus, \odot)\) is a ring of characteristic \( 6. \)
-
Let \( R \) be ring with identity \( 1. \) If \( n \) is the least positive integer such that \( n1=0,\) then the characteristic of ring R is \( 0. \)
-
The characteristic of an integral domain is either prime or \( 0. \)


