2.E: Chapter Review Exercises

Last updated
Save as PDF

Page ID: 10271

This page is a draft and is under active development.

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Exercise $\PageIndex{1}$

$\int 2 x \ln(x) dx$

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{2}$

$\int 3 \sin^3(x) \cos^3(x) dx$

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{3}$

$\int \frac{(4x^2+x+4}{x^3+x} \, dx $

Answer: Add texts here. Do not delete this text first.

For the following exercises, determine whether the statement is true or false. Justify your answer with a proof or a counterexample.

Exercise $\PageIndex{4}$

$\displaystyle ∫e^xsin(x)dx$ cannot be integrated by parts.

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{5}$

$\displaystyle ∫\frac{1}{x^4+1}dx$ cannot be integrated using partial fractions.

Answer: False

Exercise $\PageIndex{6}$

In numerical integration, increasing the number of points decreases the error.

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{7}$

Integration by parts can always yield the integral.

Answer: False

For the following exercises, evaluate the integral using the specified method.

Exercise $\PageIndex{8}$

$\displaystyle ∫x^2sin(4x)dx$ using integration by parts

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{9}$

$\displaystyle ∫\frac{1}{x^2\sqrt{x^2+16}}dx$ using trigonometric substitution

Answer: $\displaystyle −\frac{\sqrt{x^2+16}}{16x}+C$

Exercise $\PageIndex{10}$

$∫\sqrt{x}ln(x)dx$ using integration by parts

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{11}$

$\displaystyle ∫\frac{3x}{x^3+2x^2−5x−6}dx$ using partial fractions

Answer: $\displaystyle \frac{1}{10}(4ln(2−x)+5ln(x+1)−9ln(x+3))+C$

Exercise $\PageIndex{12}$

$\displaystyle ∫\frac{x^5}{(4x^2+4)^{5/2}}dx$ using trigonometric substitution

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{13}$

$\displaystyle ∫\frac{\sqrt{4−sin^2(x)}}{sin^2(x)}cos(x)dx$ using a table of integrals or a CAS

Answer: $\displaystyle −\frac{\sqrt{4−sin^2(x)}}{sin(x)}−\frac{x}{2}+C$

For the following exercises, integrate using whatever method you choose.

Exercise $\PageIndex{14}$

$\displaystyle ∫sin^2(x)cos^2(x)dx$

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{15}$

$\displaystyle ∫x^3\sqrt{x^2+2}dx$

Answer: $\displaystyle \frac{1}{15}(x^2+2)^{3/2}(3x^2−4)+C$

Exercise $\PageIndex{16}$

$\displaystyle ∫\frac{3x^2+1}{x^4−2x^3−x^2+2x}dx$

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{17}$

$\displaystyle ∫\frac{1}{x^4+4}dx$

Answer: $\displaystyle \frac{1}{16}ln(\frac{x^2+2x+2}{x^2−2x+2})−\frac{1}{8}tan^{−1}(1−x)+\frac{1}{8}tan^{−1}(x+1)+C$

Exercise $\PageIndex{18}$

$\displaystyle ∫\frac{\sqrt{3+16x^4}}{x^4}dx$

Answer: Add texts here. Do not delete this text first.

For the following exercises, approximate the integrals using the midpoint rule, trapezoidal rule, and Simpson’s rule using four subintervals, rounding to three decimals.

Exercise $\PageIndex{19}$

$\displaystyle ∫^2_1\sqrt{x^5+2}dx$

Answer: $\displaystyle M_4=3.312,T_4=3.354,S_4=3.326$

Exercise $\PageIndex{20}$

$\displaystyle ∫^{\sqrt{π}}_0e^{−sin(x^2)}dx$

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{21}$

$\displaystyle ∫^4_1\frac{ln(1/x)}{x}dx$

Answer: $\displaystyle M_4=−0.982,T_4=−0.917,S_4=−0.952$

For the following exercises, evaluate the integrals, if possible.

Exercise $\PageIndex{22}$

$\displaystyle ∫^∞_1\frac{1}{x^n}dx,$ for what values of $\displaystyle n$ does this integral converge or diverge?

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{23}$

$\displaystyle ∫^∞_1\frac{e^{−x}}{x}dx$

Answer: approximately 0.2194

For the following exercises, consider the gamma function given by $\displaystyle Γ(a)=∫^∞_0e^{−y}y^{a−1}dy.$

Exercise $\PageIndex{24}$

Show that $\displaystyle Γ(a)=(a−1)Γ(a−1).$

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{25}$

Extend to show that $\displaystyle Γ(a)=(a−1)!,$ assuming $\displaystyle a$ is a positive integer.

Answer: Add texts here. Do not delete this text first.

The fastest car in the world, the Bugati Veyron, can reach a top speed of 408 km/h. The graph represents its velocity.

$alt$

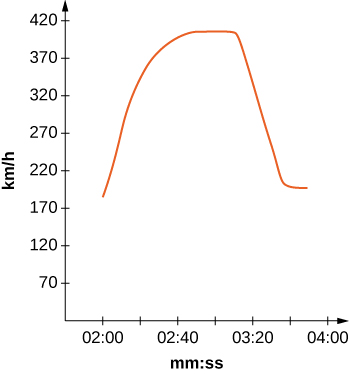
Exercise $\PageIndex{26}$

Use the graph to estimate the velocity every 20 sec and fit to a graph of the form $\displaystyle v(t)=aexp^{bx}sin(cx)+d.$ (Hint: Consider the time units.)

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{27}$

Using your function from the previous problem, find exactly how far the Bugati Veyron traveled in the 1 min 40 sec included in the graph.

Answer: Answers may vary. Ex: $\displaystyle 9.405$ km

Search

Text Color

Text Size

Margin Size

Font Type

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)

Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

Exercise \(\PageIndex{16}\)

Exercise \(\PageIndex{17}\)

Exercise \(\PageIndex{18}\)

Exercise \(\PageIndex{19}\)

Exercise \(\PageIndex{20}\)

Exercise \(\PageIndex{21}\)

Exercise \(\PageIndex{22}\)

Exercise \(\PageIndex{23}\)

Exercise \(\PageIndex{24}\)

Exercise \(\PageIndex{25}\)

Exercise \(\PageIndex{26}\)

Exercise \(\PageIndex{27}\)