5E: Chapter Review Exercises
- Page ID
- 25935
Exercise \(\PageIndex{1}\)
For the following exercises, determine whether the statement is true or false. Justify the answer with a proof or a counterexample.
1) For vectors \(\displaystyle a\) and \(\displaystyle b\) and any given scalar \(\displaystyle c, c(a⋅b)=(ca)⋅b.\)
- Answer
-
True.
2) For vectors \(\displaystyle a\) and \(\displaystyle b\) and any given scalar \(\displaystyle c, c(a×b)=(ca)×b\).
3) The symmetric equation for the line of intersection between two planes \(\displaystyle x+y+z=2\) and \(\displaystyle x+2y−4z=5\) is given by \(\displaystyle −\frac{x−1}{6}=\frac{y−1}{5}=z.\)
- Answer
-
False.
4) If \(\displaystyle a⋅b=0,\) then \(\displaystyle a\) is perpendicular to \(\displaystyle b\).
Exercise \(\PageIndex{2}\)
For the following exercises, use the given vectors to find the quantities.
5) \(\displaystyle a=9i−2j,b=−3i+j\)
a. \(\displaystyle 3a+b\)
b. \(\displaystyle |a|\)
c. \(\displaystyle a×|b×|a\)
d. \(\displaystyle b×|a\)
- Answer
-
a. \(\displaystyle ⟨24,−5⟩;\) b. \(\displaystyle \sqrt{85}\); c. Can’t dot a vector with a scalar; d. \(\displaystyle −29\)
6) \(\displaystyle a=2i+j−9k,b=−i+2k,c=4i−2j+k\)
a. \(\displaystyle 2a−b\)
b. \(\displaystyle |b×c|\)
c. \(\displaystyle b×|b×c|\)
d. \(\displaystyle c×|b×a|\)
e. \(\displaystyle proj_ab\)
7) Find the values of \(\displaystyle a\) such that vectors \(\displaystyle ⟨2,4,a⟩\) and \(\displaystyle ⟨0,−1,a⟩\) are orthogonal.
- Answer
-
\(\displaystyle a=±2\)
Exercise \(\PageIndex{3}\)
For the following exercises, find the unit vectors.
8) Find the unit vector that has the same direction as vector \(\displaystyle v\) that begins at \(\displaystyle (0,−3)\) and ends at \(\displaystyle (4,10).\)
9) Find the unit vector that has the same direction as vector \(\displaystyle v\) that begins at \(\displaystyle (1,4,10)\) and ends at \(\displaystyle (3,0,4).\)
- Answer
-
\(\displaystyle ⟨\frac{1}{\sqrt{14}},−\frac{2}{\sqrt{14}},−\frac{3}{\sqrt{14}}⟩\)
Exercise \(\PageIndex{4}\)
For the following exercises, find the area or volume of the given shapes.
10) The parallelogram spanned by vectors \(\displaystyle a=⟨1,13⟩\) and \(\displaystyle b=⟨3,21⟩\)
11) The parallelepiped formed by \(\displaystyle a=⟨1,4,1⟩\) and \(\displaystyle b=⟨3,6,2⟩,\) and \(\displaystyle c=⟨−2,1,−5⟩\)
- Answer
-
\(\displaystyle 27\)
Exercise \(\PageIndex{5}\)
For the following exercises, find the vector and parametric equations of the line with the given properties.
12) The line that passes through point \(\displaystyle (2,−3,7)\) that is parallel to vector \(\displaystyle ⟨1,3,−2⟩\)
13) The line that passes through points \(\displaystyle (1,3,5)\) and \(\displaystyle (−2,6,−3)\)
- Answer
-
\(\displaystyle x=1−3t,y=3+3t,z=5−8t,r(t)=(1−3t)i+3(1+t)j+(5−8t)k\)
Exercise \(\PageIndex{6}\)
For the following exercises, find the equation of the plane with the given properties.
14) The plane that passes through point \(\displaystyle (4,7,−1)\) and has normal vector \(\displaystyle n=⟨3,4,2⟩\)
15) The plane that passes through points \(\displaystyle (0,1,5),(2,−1,6),\) and \(\displaystyle (3,2,5).\)
- Answer
-
\(\displaystyle −x+3y+8z=43\)
Exercise \(\PageIndex{7}\)
For the following exercises, find the traces for the surfaces in planes \(\displaystyle x=k,y=k\), and \(\displaystyle z=k.\) Then, describe and draw the surfaces.
16) \(\displaystyle 9x^2+4y^2−16y+36z^2=20\)
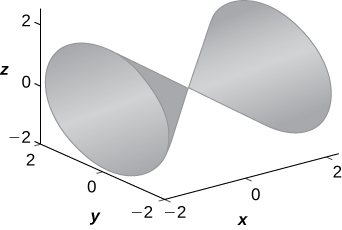
17) \(\displaystyle x^2=y^2+z^2\)
- Answer
-
\(\displaystyle x=k\) trace: \(\displaystyle k^2=y^2+z^2\) is a circle, \(\displaystyle y=k\) trace: \(\displaystyle x^2−z^2=k^2\) is a hyperbola (or a pair of lines if \(\displaystyle k=0), z=k\) trace: \(\displaystyle x^2−y^2=k^2\) is a hyperbola (or a pair of lines if \(\displaystyle k=0\)). The surface is a cone.
Exercise \(\PageIndex{8}\)
For the following exercises, write the given equation in cylindrical coordinates and spherical coordinates.
18) \(\displaystyle x^2+y^2+z^2=144\)
19) \(\displaystyle z=x^2+y^2−1\)
- Answer
-
Cylindrical: \(\displaystyle z=r^2−1,\) spherical: \(\displaystyle cosφ=ρsin^2φ−\frac{1}{ρ}\)
Exercise \(\PageIndex{9}\)
For the following exercises, convert the given equations from cylindrical or spherical coordinates to rectangular coordinates. Identify the given surface.
20) \(\displaystyle ρ^2(sin^2(φ)−cos^2(φ))=1\)
21) \(\displaystyle r^2−2rcos(θ)+z^2=1\)
- Answer
-
\(\displaystyle x^2−2x+y^2+z^2=1\), sphere
Exercise \(\PageIndex{10}\)
For the following exercises, consider a small boat crossing a river.
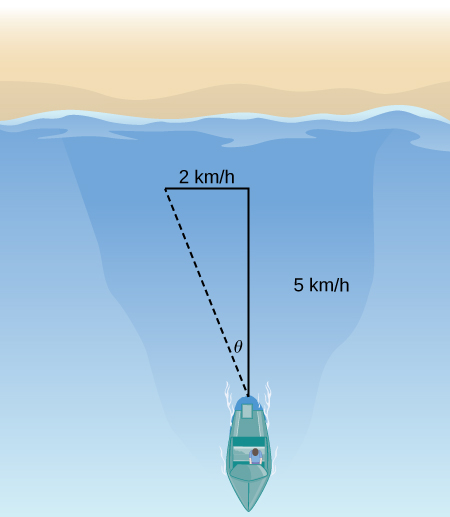
22) If the boat velocity is \(\displaystyle 5\)km/h due north in still water and the water has a current of \(\displaystyle 2\) km/h due west (see the following figure), what is the velocity of the boat relative to shore? What is the angle \(\displaystyle θ\) that the boat is actually traveling?
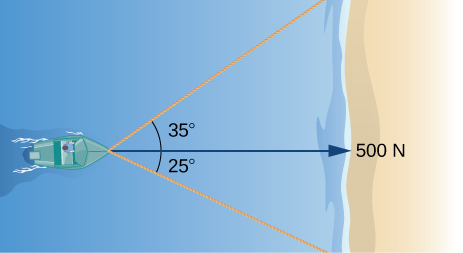
23) When the boat reaches the shore, two ropes are thrown to people to help pull the boat ashore. One rope is at an angle of \(\displaystyle 25°\) and the other is at \(\displaystyle 35°\). If the boat must be pulled straight and at a force of \(\displaystyle 500N\), find the magnitude of force for each rope (see the following figure).
- Answer
-
331 N, and 244 N
24) An airplane is flying in the direction of 52° east of north with a speed of 450 mph. A strong wind has a bearing 33° east of north with a speed of 50 mph. What is the resultant ground speed and bearing of the airplane?
25) Calculate the work done by moving a particle from position \(\displaystyle (1,2,0)\) to \(\displaystyle (8,4,5)\) along a straight line with a force \(\displaystyle F=2i+3j−k.\)
- Answer
-
\(\displaystyle 15J\)
Exercise \(\PageIndex{11}\)
The following problems consider your unsuccessful attempt to take the tire off your car using a wrench to loosen the bolts. Assume the wrench is \(\displaystyle 0.3\)m long and you are able to apply a 200-N force.
26) Because your tire is flat, you are only able to apply your force at a \(\displaystyle 60°\) angle. What is the torque at the center of the bolt? Assume this force is not enough to loosen the bolt.
27) Someone lends you a tire jack and you are now able to apply a 200-N force at an \(\displaystyle 80°\) angle. Is your resulting torque going to be more or less? What is the new resulting torque at the center of the bolt? Assume this force is not enough to loosen the bolt.
- Answer
-
More, \(\displaystyle 59.09 J\)

