6.1E: Exercises
- Page ID
- 25937
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Exercise \(\PageIndex{1}\) functional value
For the following exercises, evaluate each function at the indicated values.
1) \(\displaystyle W(x,y)=4x^2+y^2.\) Find \(\displaystyle W(2,−1), W(−3,6).\)
- Answer
-
Solution:\(\displaystyle 17,72\)
2) \(\displaystyle W(x,y)=4x^2+y^2\). Find \(\displaystyle W(2+h,3+h).\)
3) The volume of a right circular cylinder is calculated by a function of two variables, \(\displaystyle V(x,y)=πx^2y,\) where \(\displaystyle x\) is the radius of the right circular cylinder and \(\displaystyle y\) represents the height of the cylinder. Evaluate \(\displaystyle V(2,5)\) and explain what this means.
- Answer
-
Solution:\(\displaystyle 20π.\) This is the volume when the radius is \(\displaystyle 2\) and the height is \(\displaystyle 5\).
4) An oxygen tank is constructed of a right cylinder of height \(\displaystyle y\) and radius \(\displaystyle x\) with two hemispheres of radius \(\displaystyle x\) mounted on the top and bottom of the cylinder. Express the volume of the cylinder as a function of two variables, \(\displaystyle x\) and \(\displaystyle y\), find \(\displaystyle V(10,2)\), and explain what this means.
Exercise \(\PageIndex{2}\) Domain
For the following exercises, find the domain of the function.
1) \(\displaystyle V(x,y)=4x^2+y^2\)
- Answer
-
Solution:All points in the \(\displaystyle xy-plane\)
2) \(\displaystyle f(x,y)=\sqrt{x^2+y^2−4}\)
3) \(\displaystyle f(x,y)=4ln(y^2−x)\)
- Answer
-
Solution:\(\displaystyle x<y^2\)
4) \(\displaystyle g(x,y)=\sqrt{16−4x^2−y^2}\)
5) \(\displaystyle z(x,y)=y^2−x^2\)
- Answer
-
Solution:All real ordered pairs in the \(\displaystyle xy-plane\) of the form \(\displaystyle (a,b)\)
6) \(\displaystyle f(x,y)=\frac{y+2}{x^2}\)
Exercise \(\PageIndex{3}\) range
Find the range of the functions.
1) \(\displaystyle g(x,y)=\sqrt{16−4x^2−y^2}\)
- Answer
-
Solution:\(\displaystyle \{z|0≤z≤4 \}\)
2) \(\displaystyle V(x,y)=4x^2+y^2\)
3) \(\displaystyle z=y^2−x^2\)
- Answer
-
Solution:The set \(\displaystyle R\).
Exercise \(\PageIndex{4}\) Level Curves
For the following exercises, find the level curves of each function at the indicated value of \(\displaystyle c\) to visualize the given function.
1) \(\displaystyle z(x,y)=y^2−x^2, c=1\)
2) \(\displaystyle z(x,y)=y^2−x^2, c=4\)
- Answer
-
Solution:\(\displaystyle y^2−x^2=4,\) a hyperbola
3) \(\displaystyle g(x,y)=x^2+y^2;c=4,c=9\)
4) \(\displaystyle g(x,y)=4−x−y;c=0,4\)
- Answer
-
Solution:\(\displaystyle 4=x+y,\) a line; \(\displaystyle x+y=0,\) line through the origin
5) \(\displaystyle h(x,y)=2x−y;c=0,−2,2\)
- Answer
-
Solution:\(\displaystyle 2x−y=0,2x−y=−2,2x−y=2;\) three lines
6) \(\displaystyle f(x,y)=x^2−y;c=1,2\)
7) \(\displaystyle g(x,y)=\frac{x}{x+y};c=−1,0,2\)
- Answer
-
Solution:\(\displaystyle \frac{x}{x+y}=−1,\frac{x}{x+y}=0,\frac{x}{x+y}=2\)
8) \(\displaystyle g(x,y)=x^3−y;c=−1,0,2\)
9) \(\displaystyle g(x,y)=e^{xy};c=\frac{1}{2},3\)
- Answer
-
Solution:\(\displaystyle e^{xy}=\frac{1}{2},e^{xy}=3\)
10) \(\displaystyle f(x,y)=x^2;c=4,9\)
12) \(\displaystyle f(x,y)=xy−x;c=−2,0,2\)
- Answer
-
Solution:\(\displaystyle xy−x=−2,xy−x=0,xy−x=2\)
13) \(\displaystyle h(x,y)=ln(x^2+y^2);c=−1,0,1\)
14) \(\displaystyle g(x,y)=ln(\frac{y}{x^2});c=−2,0,2\)
- Answer
-
Solution:\(\displaystyle e^{−2}x^2=y,y=x^2,y=e^2x^2\)
15) \(\displaystyle z=f(x,y)=\sqrt{x^2+y^2}, c=3\)
16) \(\displaystyle f(x,y)=\frac{y+2}{x^2}, c=\)any constant
- Answer
-
Solution:The level curves are parabolas of the form \(\displaystyle y=cx^2−2.\)
Exercise \(\PageIndex{5}\) Vertical Traces
For the following exercises, find the vertical traces of the functions at the indicated values of \(\displaystyle x\) and \(\displaystyle y\), and plot the traces.
1) \(\displaystyle z=4−x−y;x=2\)
2) \(\displaystyle f(x,y)=3x+y^3,x=1\)
- Answer
-
Solution:\(\displaystyle z=3+y^3,\) a curve in the zy-plane with rulings parallel to the \(\displaystyle x-axis\)
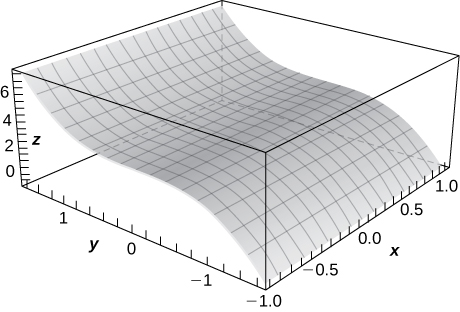
3) \(\displaystyle z=cos\sqrt{x^2+y^2} x=1\)
Exercise \(\PageIndex{6}\) Domain
Find the domain of the following functions.
1) \(\displaystyle z=\sqrt{100−4x^2−25y^2}\)
- Answer
-
Solution:\(\displaystyle \frac{x^2}{25}+\frac{y^2}{4}≤1\)
2) \(\displaystyle z=ln(x−y^2)\)
3) \(\displaystyle f(x,y,z)=\frac{1}{\sqrt{36−4x^2−9y^2−z^2}}\)
- Answer
-
Solution:\(\displaystyle \frac{x^2}{9}+\frac{y^2}{4}+\frac{z^2}{36}<1\)
4) \(\displaystyle f(x,y,z)=\sqrt{49−x^2−y^2−z^2}\)
5) \(\displaystyle f(x,y,z)=\sqrt[3]{16−x^2−y^2−z^2}\)
- Answer
-
Solution:All points in \(\displaystyle xyz-space\)
6) \(\displaystyle f(x,y)=cos\sqrt{x^2+y^2}\)
Exercise \(\PageIndex{7}\) Graph
For the following exercises, plot a graph of the function.
1) \(\displaystyle z=f(x,y)=\sqrt{x^2+y^2}\)
- Answer
-
Solution:
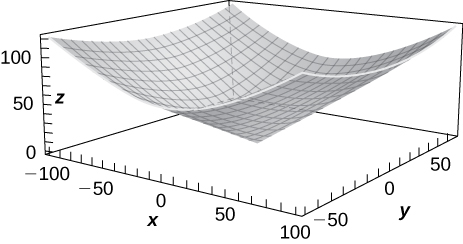
2) \(\displaystyle z=x^2+y^2\)
3) Use technology to graph \(\displaystyle z=x^2y.\)
- Answer
-
Solution:
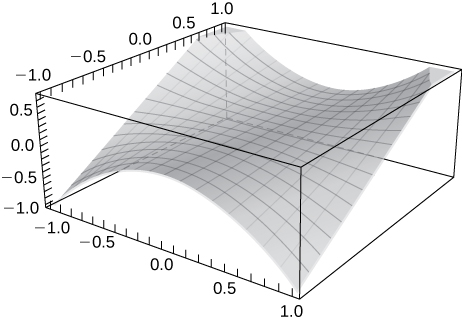
Exercise \(\PageIndex{8}\) Level curves
Sketch the following by finding the level curves. Verify the graph using technology.
1) \(\displaystyle f(x,y)=\sqrt{4−x^2−y^2}\)
2) \(\displaystyle f(x,y)=2−\sqrt{x^2+y^2}\)
- Answer
-
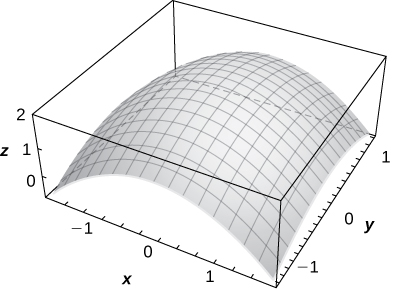
3) \(\displaystyle z=1+e^{−x^2−y^2}\)
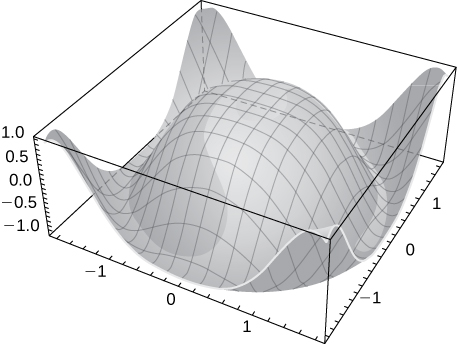
4) \(\displaystyle z=cos\sqrt{x^2+y^2}\)
- Answer
-
Solution:
5) \(\displaystyle z=y^2−x^2\)
Exercise \(\PageIndex{9}\) Contour lines
1) Describe the contour lines for several values of \(\displaystyle c\) for \(\displaystyle z=x^2+y^2−2x−2y.\)
- Answer
-
Solution:The contour lines are circles.
Exercise \(\PageIndex{10}\) level surface
Find the level surface for the functions of three variables and describe it.
1) \(\displaystyle w(x,y,z)=x−2y+z,c=4\)
2) \(\displaystyle w(x,y,z)=x^2+y^2+z^2,c=9\)
- Answer
-
Solution:\(\displaystyle x^2+y^2+z^2=9\), a sphere of radius \(\displaystyle 3\)
3) \(\displaystyle w(x,y,z)=x^2+y^2−z^2,c=−4\)
4) \(\displaystyle w(x,y,z)=x^2+y^2−z^2,c=4\)
- Answer
-
Solution:\(\displaystyle x^2+y^2−z^2=4,\) a hyperboloid of one sheet
5) \(\displaystyle w(x,y,z)=9x^2−4y^2+36z^2,c=0\)
Exercise \(\PageIndex{11}\) level curve at a given point
For the following exercises, find an equation of the level curve of \(\displaystyle f\) that contains the point \(\displaystyle P\).
1) \(\displaystyle f(x,y)=1−4x^2−y^2,P(0,1)\)
- Answer
-
Solution:\(\displaystyle 4x^2+y^2=1,\)
2) \(\displaystyle g(x,y)=y^2arctanx,P(1,2)\)
3) \(\displaystyle g(x,y)=e^{xy}(x^2+y^2),P(1,0)\)
- Answer
-
Solution:\(\displaystyle 1=e^{xy}(x^2+y^2)\)
Exercise \(\PageIndex{12}\) Applications
1) The strength \(\displaystyle E\) of an electric field at point \(\displaystyle (x,y,z)\) resulting from an infinitely long charged wire lying along the \(\displaystyle y-axis\) is given by \(\displaystyle E(x,y,z)=k/\sqrt{x^2+y^2}\), where \(\displaystyle k\) is a positive constant. For simplicity, let \(\displaystyle k=1\) and find the equations of the level surfaces for \(\displaystyle E=10\) and \(\displaystyle E=100.\)
2) A thin plate made of iron is located in the \(\displaystyle xy-plane.\) The temperature \(\displaystyle T\) in degrees Celsius at a point \(\displaystyle P(x,y)\) is inversely proportional to the square of its distance from the origin. Express \(\displaystyle T\) as a function of \(\displaystyle x\) and \(\displaystyle y\).
- Answer
-
Solution:\(\displaystyle T(x,y)=\frac{k}{x^2+y^2}\)
3) Refer to the preceding problem. Using the temperature function found there, determine the proportionality constant if the temperature at point \(\displaystyle P(1,2)\) is \(\displaystyle 50°C.\) Use this constant to determine the temperature at point \(\displaystyle Q(3,4).\)
4) Refer to the preceding problem. Find the level curves for \(\displaystyle T=40°C\) and \(\displaystyle T=100°C,\) and describe what the level curves represent.
- Answer
-
Solution:\(\displaystyle x^2+y^2=\frac{k}{40}, x^2+y^2=\frac{k}{100}\). The level curves represent circles of radii \(\displaystyle \sqrt{10k}/20\) and \(\displaystyle \sqrt{k}/10\)

