7.6: Calculating Centers of Mass and Moments of Inertia

We have already discussed a few applications of multiple integrals, such as finding areas, volumes, and the average value of a function over a bounded region. In this section we develop computational techniques for finding the center of mass and moments of inertia of several types of physical objects, using double integrals for a lamina (flat plate) and triple integrals for a three-dimensional object with variable density. The density is usually considered to be a constant number when the lamina or the object is homogeneous; that is, the object has uniform density.

Center of Mass in Two Dimensions

The center of mass is also known as the center of gravity if the object is in a uniform gravitational field. If the object has uniform density, the center of mass is the geometric center of the object, which is called the centroid. Figure $\PageIndex{1}$ shows a point $P$ as the center of mass of a lamina. The lamina is perfectly balanced about its center of mass.

Figure $\PageIndex{1}$: A lamina is perfectly balanced on a spindle if the lamina’s center of mass sits on the spindle.

To find the coordinates of the center of mass $P(\bar{x},\bar{y})$ of a lamina, we need to find the moment $M_x$ of the lamina about the $x$-axis and the moment $M_y$ about the $y$-axis. We also need to find the mass $m$ of the lamina. Then

$$\bar{x} = \dfrac{M_y}{m}$$

and

$$\bar{y} = \dfrac{M_x}{m}.$$

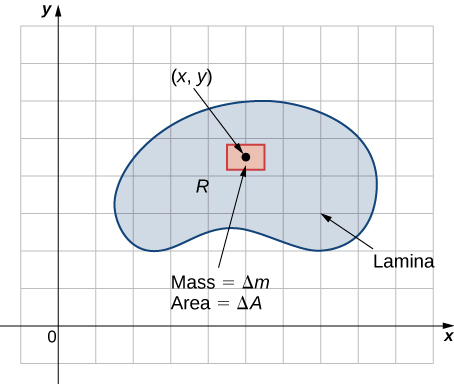
Refer to Moments and Centers of Mass for the definitions and the methods of single integration to find the center of mass of a one-dimensional object (for example, a thin rod). We are going to use a similar idea here except that the object is a two-dimensional lamina and we use a double integral.

If we allow a constant density function, then $\bar{x} = \dfrac{M_y}{m}$ and $\bar{y} = \dfrac{M_x}{m}$ give the centroid of the lamina.

Suppose that the lamina occupies a region $R$ in the $xy$-plane and let $\rho (x,y)$ be its density (in units of mass per unit area) at any point $(x,y)$. Hence,

$$\rho(x,y) = \lim_{\Delta A \rightarrow 0} \dfrac{\Delta m}{\Delta A}$$

where $\Delta m$ and $\Delta A$ are the mass and area of a small rectangle containing the point $(x,y)$ and the limit is taken as the dimensions of the rectangle go to $0$ (see the following figure).

Figure $\PageIndex{2}$: The density of a lamina at a point is the limit of its mass per area in a small rectangle about the point as the area goes to zero.

Just as before, we divide the region $R$ into tiny rectangles $R_{ij}$ with area $\Delta A$ and choose $(x_{ij}^*, y_{ij}^*)$ as sample points. Then the mass $m_{ij}$ of each $R_{ij}$ is equal to $\rho (x_{ij}^*, y_{ij}^*) \Delta A$ (Figure $\PageIndex{2}$). Let $k$ and $l$ be the number of subintervals in $x$ and $y$ respectively. Also, note that the shape might not always be rectangular but the limit works anyway, as seen in previous sections.

Figure $\PageIndex{3}$: Subdividing the lamina into tiny rectangles $R_{ij}$ each containing a sample point $(x_{ij}^*,y_{ij}^*)$.

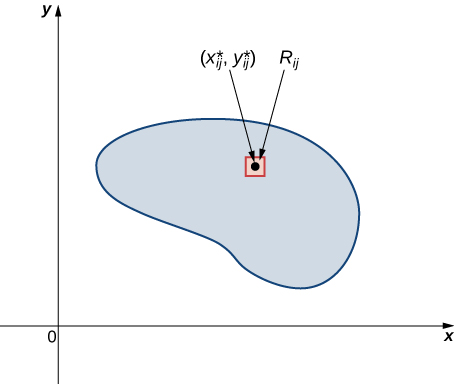
Hence, the mass of the lamina is

$$m =\lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l m_{ij} = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l \rho(x_{ij}^*,y_{ij}^*) \Delta A = \iint_R \rho(x,y) dA.$$

Let’s see an example now of finding the total mass of a triangular lamina.

Example $\PageIndex{1}$: Finding the Total Mass of a Lamina

Consider a triangular lamina $R$ with vertices $(0,0), \, (0,3), \, (3,0)$ and with density $\rho(x,y) = xy \, kg/m^2$. Find the total mass.

Solution

A sketch of the region $R$ is always helpful, as shown in the following figure.

Figure $\PageIndex{4}$: A lamina in the $xy$-plane with density $\rho (x,y) = xy$.

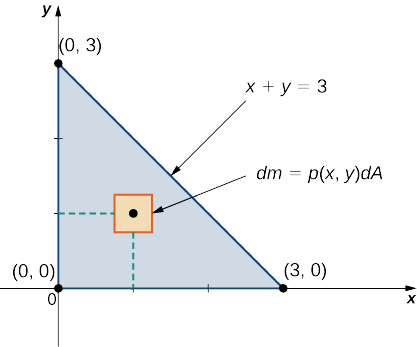
Using the expression developed for mass, we see that

$$m = \iint_R \, dm = \iint_R \rho (x,y) dA = \int_{x=0}^{x=3} \int_{y=0}^{y=3-x} xy \, dy \, dx = \int_{x=0}^{x=3} \left[ \left. x \dfrac{y^2}{2} \right|_{y=0}^{y=3} \right] \, dx = \int_{x=0}^{x=3} \dfrac{1}{2} x (3 - x)^2 dx = \left.\left[ \dfrac{9x^2}{4} - x^3 + \dfrac{x^4}{8} \right]\right|_{x=0}^{x=3} = \dfrac{27}{8}.$$

The computation is straightforward, giving the answer $m = \dfrac{27}{8} \, kg$.

Exercise $\PageIndex{1}$

Consider the same region $R$ as in the previous example, and use the density function $\rho (x,y) = \sqrt{xy}$. Find the total mass.

Answer

$\dfrac{9\pi}{8} \, kg$

Now that we have established the expression for mass, we have the tools we need for calculating moments and centers of mass. The moment $M_z$ about the $x$-axis for $R$ is the limit of the sums of moments of the regions $R_{ij}$ about the $x$-axis. Hence

$$M_x = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*)m_{ij} = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*) \rho(x_{ij}^*,y_{ij}^*) \Delta A = \iint_R y\rho (x,y) dA$$

Similarly, the moment $M_y$ about the $y$-axis for $R$ is the limit of the sums of moments of the regions $R_{ij}$ about the $y$-axis. Hence

$$M_x = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*)m_{ij} = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*) \rho(x_{ij}^*,y_{ij}^*) \Delta A = \iint_R x\rho (x,y) dA$$

Example $\PageIndex{2}$: Finding Moments

Consider the same triangular lamina $R$ with vertices $(0,0), \, (0,3), \, (3,0)$ and with density $\rho (x,y) = xy$. Find the moments $M_x$ and $M_y$.

Solution

Use double integrals for each moment and compute their values:

$$M_x = \iint_R y\rho (x,y) dA = \int_{x=0}^{x=3} \int_{y=0}^{y=3-x} x y^2 \, dy \, dx = \dfrac{81}{20},$$

$$M_y = \iint_R x\rho (x,y) dA = \int_{x=0}^{x=3} \int_{y=0}^{y=3-x} x^2 y \, dy \, dx = \dfrac{81}{20},$$

The computation is quite straightforward.

Exercise $\PageIndex{2}$

Consider the same lamina $R$ as above and use the density function $\rho (x,y) = \sqrt{xy}$. Find the moments $M_x$ and $M_y$.

Answer

$M_x = \dfrac{81\pi}{64}$ and $M_y = \dfrac{81\pi}{64}$

Finally we are ready to restate the expressions for the center of mass in terms of integrals. We denote the x-coordinate of the center of mass by $\bar{x}$ and the y-coordinate by $\bar{y}$. Specifically,

$$\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x\rho (x,y) dA}{\iint_R \rho (x,y)dA}$$

and

$$\bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y\rho (x,y) dA}{\iint_R \rho (x,y)dA}$$

Example $\PageIndex{3}$: center of mass

Again consider the same triangular region $R$ with vertices $(0,0), \, (0,3), \, (3,0)$ and with density function $\rho (x,y) = xy$. Find the center of mass.

Solution

Using the formulas we developed, we have

$$\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x\rho (x,y) dA}{\iint_R \rho (x,y)dA} = \dfrac{81/20}{27/8} = \dfrac{6}{5},$$

$$\bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y\rho (x,y) dA}{\iint_R \rho (x,y)dA} = \dfrac{81/20}{27/8} = \dfrac{6}{5}.$$

Therefore, the center of mass is the point $\left(\dfrac{6}{5},\dfrac{6}{5}\right).$

Analysis

If we choose the density $\rho(x,y)$ instead to be uniform throughout the region (i.e., constant), such as the value 1 (any constant will do), then we can compute the centroid,

$$x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R dA} = \dfrac{9/2}{9/2} = 1,$$

$$y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R dA} = \dfrac{9/2}{9/2} = 1.$$

Notice that the center of mass $\left(\dfrac{6}{5},\dfrac{6}{5}\right)$ is not exactly the same as the centroid $(1,1)$ of the triangular region. This is due to the variable density of $R$ If the density is constant, then we just use $\rho(x,y) = c$ (constant). This value cancels out from the formulas, so for a constant density, the center of mass coincides with the centroid of the lamina.

Exercise $\PageIndex{3}$

Again use the same region $R$ as above and use the density function $\rho (x,y) = \sqrt{xy}$. Find the center of mass.

Answer

$\bar{x} = \dfrac{M_y}{m} = \dfrac{81\pi/64}{9\pi/8} = \dfrac{9}{8}$ and $\bar{y} = \dfrac{M_x}{m} = \dfrac{81\pi}{9\pi/8} = \dfrac{0}{8}$.

Once again, based on the comments at the end of Example $\PageIndex{3}$, we have expressions for the centroid of a region on the plane:

$$x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R dA} \, \text{and} \, y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R dA}.$$

We should use these formulas and verify the centroid of the triangular region R referred to in the last three examples.

Example $\PageIndex{4}$: Finding Mass, Moments, and Center of Mass

Find the mass, moments, and the center of mass of the lamina of density $\rho(x,y) = x + y$ occupying the region $R$ under the curve $y = x^2$ in the interval $0 \leq x \leq 2$ (see the following figure).

Figure $\PageIndex{5}$: Locating the center of mass of a lamina $R$ with density $\rho(x,y) = x+y$.

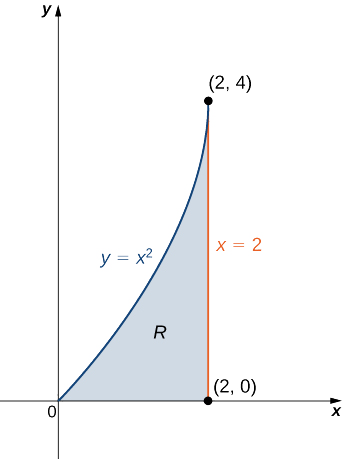
Solution

First we compute the mass $m$. We need to describe the region between the graph of $y = x^2$ and the vertical lines $x = 0$ and $x = 2$:

$$m = \iint_R dm = \iint_R \rho (x,y) dA = \int_{x=0}{x=2} \int_{y=0}^{y=x^2} (x + y) dy \, dx = \int_{x=0}^{x=2} \left[\left. xy + \dfrac{y^2}{2}\right|_{y=0}^{y=x^2} \right] dx$$

$$= \int_{x=0}^{x=2} \left[ x^3 + \dfrac{x^4}{2} \right] dx = \left.\left[ \dfrac{x^4}{4} + \dfrac{x^5}{10}\right] \right|_{x=0}^{x=2} = \dfrac{36}{5}.$$

Now compute the moments $M_x$ and $M_y$:

$$M_x = \iint_R y \rho (x,y) dA = \int_{x=0}^{x=2} \int_{y=0}^{y=x^2} y(x + y) dy \, dx = \dfrac{80}{7},$$

$$M_y = \iint_R x \rho (x,y) dA = \int_{x=0}^{x=2} \int_{y=0}^{y=x^2} x(x + y) dy \, dx = \dfrac{176}{15}.$$

Finally, evaluate the center of mass,

$$\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x \rho (x,y) dA}{\iint_R \rho (x,y)dA} = \dfrac{176/15}{36/5} = \dfrac{44}{27},$$

$$\bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y \rho (x,y) dA}{\iint_R \rho (x,y)dA} = \dfrac{80/7}{36/5} = \dfrac{100}{63}.$$

Hence the center of mass is $(\bar{x},\bar{y}) = \left(\dfrac{44}{27}, \dfrac{100}{63} \right)$.

Exercise $\PageIndex{4}$

Calculate the mass, moments, and the center of mass of the region between the curves $y = x$ and $y = x^2$ with the density function $\rho(x,y) = x$ in the interval $0 \leq x \leq 1$.

Answer

$\bar{x} = \dfrac{M_y}{m} = \dfrac{1/20}{1/12} = \dfrac{3}{5}$ and $\bar{y} = \dfrac{M_x}{m} = \dfrac{1/24}{1/12} = \dfrac{1}{2}$

Example $\PageIndex{5}$: Finding a Centroid

Find the centroid of the region under the curve $y = e^x$ over the interval $1 \leq x \leq 3$ (Figure $\PageIndex{6}$).

Figure $\PageIndex{6}$: Finding a centroid of a region below the curve $y = e^x$.

Solution

To compute the centroid, we assume that the density function is constant and hence it cancels out:

$$x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R dA} \, and \, y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R dA},$$

$$x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R dA} = \dfrac{\int_{x=1}^{x=3} \int_{y=0}^{y=e^x} x \, dy \, dx}{\int_{x=1}^{x=3} \int_{y=0}^{y=e^x} dy \, dx} = \dfrac{\int_{x=1}^{x=3} xe^x dx}{\int_{x=1}^{x=3} e^x dx} = \dfrac{2e^3}{e^3 - e} = \dfrac{2e^2}{e^2 - 1},$$

$$y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R dA} = \dfrac{\int_{x=1}^{x=3} \int_{y=0}^{y=e^x} y \, dy \, dx}{\int_{x=1}^{x=3} \int_{y=0}^{y=e^x} dy \, dx} = \dfrac{\int_{x=1}^{x=3} \dfrac{e^{2x}}{2} dx}{\int_{x=1}^{x=3} e^x dx} =\dfrac{\dfrac{1}{4} e^2 (e^4 - 1)}{e(e^2 - 1)} = \dfrac{1}{4} e(e^2 + 1).$$

Thus the centroid of the region is

$$(x_c,y_c) = \left( \dfrac{2e^2}{e^2 - 1}, \dfrac{1}{4} e(e^2 + 1)\right).$$

Exercise $\PageIndex{5}$

Calculate the centroid of the region between the curves $y = x$ and $y = \sqrt{x}$ with uniform density in the interval $0 \leq x \leq 1$.

Answer

$x_c = \dfrac{M_y}{m} = \dfrac{1/15}{1/6} = \dfrac{2}{5}$ and $y_c = \dfrac{M_x}{m} = \dfrac{1/12}{1/6} = \dfrac{1}{2}$

Moments of Inertia

For a clear understanding of how to calculate moments of inertia using double integrals, we need to go back to the general definition in Section $6.6$. The moment of inertia of a particle of mass $m$ about an axis is $mr^2$ where $r$ is the distance of the particle from the axis. We can see from Figure $PageIndex{3}$ that the moment of inertia of the subrectangle $R_{ij}$ about the $x$-axis is $(y_{ij}^*)^2 \rho(x_{ij}^*,y_{ij}^*) \Delta A$. Similarly, the moment of inertia of the subrectangle $R_{ij}$ about the $y$-axis is $(x_{ij}^*)^2 \rho(x_{ij}^*,y_{ij}^*) \Delta A$. The moment of inertia is related to the rotation of the mass; specifically, it measures the tendency of the mass to resist a change in rotational motion about an axis.

The moment of inertia $I_x$ about the $x$-axis for the region $R$ is the limit of the sum of moments of inertia of the regions $R_{ij}$ about the $x$-axis. Hence

$$I_x = \lim_{k,l\rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*)^2 m_{ij} = \lim_{k,l\rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*)^2 \rho (x_{ij}^*, y_{ij}^*) \Delta A = \iint_R y^2 \rho(x,y)dA.$$

Similarly, the moment of inertia $I_y$ about the $y$-axis for $R$ is the limit of the sum of moments of inertia of the regions $R_{ij}$ about the $y$-axis. Hence

$$I_y = \lim_{k,l\rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*)^2 m_{ij} = \lim_{k,l\rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*)^2 \rho (x_{ij}^*, y_{ij}^*) \Delta A = \iint_R x^2 \rho(x,y)dA.$$

Sometimes, we need to find the moment of inertia of an object about the origin, which is known as the polar moment of inertia. We denote this by $I_0$ and obtain it by adding the moments of inertia $I_x$ and $I_y$. Hence

$$I_0 = I_x + I_y = \iint_R (x^2 + y^2) \rho (x,y) dA.$$

All these expressions can be written in polar coordinates by substituting $x = r \, \cos \, \theta, \, y = r \, \sin \, \theta$, and $dA = r \, dr \, d\theta$. For example, $I_0 = \iint_R r^2 \rho (r \, \cos \, \theta, \, r \, \sin \, \theta)dA$.

Example $\PageIndex{6}$: Finding Moments of Inertia for a Triangular Lamina

Use the triangular region $R$ with vertices $(0,0), \, (2,2)$, and $(2,0)$ and with density $\rho (x,y) = xy$ as in previous examples. Find the moments of inertia.

Solution

Using the expressions established above for the moments of inertia, we have

$$I_x = \iint_R y^2 \rho(x,y) dA = \int_{x=0}^{x=2} \int_{y=0}^{y=x} xy^3 dy \, dx = \dfrac{8}{3},$$

$$I_y = \iint_R x^2 \rho(x,y) dA = \int_{x=0}^{x=2} \int_{y=0}^{y=x} x^3y dy \, dx = \dfrac{16}{3},$$

$$I_0 = \iint_R (x^2 + y^2) \rho(x,y) dA = \int_0^2 \int_0^x (x^2 + y^2) xy \, dy \, dx = I_x + I_y = 8$$

Exercise $\PageIndex{6}$

Again use the same region $R$ as above and the density function $\rho (x,y) = \sqrt{xy}$. Find the moments of inertia.

Answer

$$I_x = \int_{x=0}^{x=2} \int_{y=0}^{y=x} y^2 \sqrt{xy} \, dy \, dx = \dfrac{64}{35}$$ and

$$I_y = \int_{x=0}^{x=2} \int_{y=0}^{y=x} x^2 \sqrt{xy} \, dy \, dx = \dfrac{64}{35}.$$ Also,

$$I_0 = \int_{x=0}^{x=2} \int_{y=0}^{y=x} (x^2 + y^2) \sqrt{xy} \, dy \, dx = \dfrac{128}{21}$$

As mentioned earlier, the moment of inertia of a particle of mass $m$ about an axis is $mr^2$ where $r$ is the distance of the particle from the axis, also known as the radius of gyration.

Hence the radii of gyration with respect to the $x$-axis, the $y$-axis and the origin are

$$R_x = \sqrt{\dfrac{I_x}{m}}, \, R_y = \sqrt{\dfrac{I_y}{m}}, \, and \, R_0 = \sqrt{\dfrac{I_0}{m}},$$

respectively. In each case, the radius of gyration tells us how far (perpendicular distance) from the axis of rotation the entire mass of an object might be concentrated. The moments of an object are useful for finding information on the balance and torque of the object about an axis, but radii of gyration are used to describe the distribution of mass around its centroidal axis. There are many applications in engineering and physics. Sometimes it is necessary to find the radius of gyration, as in the next example.

Example $\PageIndex{7}$: Finding the Radius of Gyration for a Triangular Lamina

Consider the same triangular lamina $R$ with vertices $(0,0), \, (2,2)$, and $(2,0)$ and with density $\rho(x,y) = xy$ as in previous examples. Find the radii of gyration with respect to the $x$-axis the $y$-axis and the origin.

Solution

If we compute the mass of this region we find that $m = 2$. We found the moments of inertia of this lamina in Example $\PageIndex{4}$. From these data, the radii of gyration with respect to the $x$-axis, $y$-axis and the origin are, respectively,

$$\begin{align} R_x &= \sqrt{\dfrac{I_x}{m}} = \sqrt{\dfrac{8/3}{2}} = \sqrt{\dfrac{8}{6}} = \dfrac{2\sqrt{3}}{3},\\R_y &= \sqrt{\dfrac{I_y}{m}} = \sqrt{\dfrac{16/3}{2}} = \sqrt{\dfrac{8}{3}} = \dfrac{2\sqrt{6}}{3}, \\R_0 &= \sqrt{\dfrac{I_0}{m}} = \sqrt{\dfrac{8}{2}} = \sqrt{4} = 2.\end{align}$$

Exercise $\PageIndex{7}$

Use the same region $R$ from Example $\PageIndex{7}$ and the density function $\rho (x,y) = \sqrt{xy}$. Find the radii of gyration with respect to the $x$-axis, the $y$-axis, and the origin.

Hint

Follow the steps shown in the previous example.

Answer

$R_x = \dfrac{6\sqrt{35}}{35}, \, R_y = \dfrac{6\sqrt{15}}{15},$ and $R_0 = \dfrac{4\sqrt{42}}{7}$.

Center of Mass and Moments of Inertia in Three Dimensions

All the expressions of double integrals discussed so far can be modified to become triple integrals.

Definition

If we have a solid object $Q$ with a density function $\rho(x,y,z)$ at any point $(x,y,z)$ in space, then its mass is

$$m = \iiint_Q \rho(x,y,z) dV.$$

Its moments about the $xy$-plane the $xz$-plane and the $yz$-plane are

$$M_{xy} = \iiint_Q z\rho (x,y,z) dV, \, M_{xz} = \iiint_Q y\rho(x,y,z) dV, \, M_{yz} = \iiint_Q x\rho(x,y,z) dV.$$

If the center of mass of the object is the point $(\bar{x}, \bar{y}, \bar{z})$, then

$$\bar{x} = \dfrac{M_{yz}}{m}, \, \bar{y} = \dfrac{M_{xz}}{m}, \, \bar{z} = \dfrac{M_{xy}}{m}.$$

Also, if the solid object is homogeneous (with constant density), then the center of mass becomes the centroid of the solid. Finally, the moments of inertia about the $yz$-plane, $xz$-plane, and the $xy$-plane are

$$I_x = \iiint_Q (y^2 + z^2) \, \rho (x,y,z) \, dV,$$

$$I_y = \iiint_Q (x^2 + z^2) \, \rho (x,y,z) \, dV,$$

$$I_z = \iiint_Q (x^2 + y^2) \, \rho (x,y,z) \, dV.$$

Example $\PageIndex{8}$: Finding the Mass of a Solid

Suppose that $Q$ is a solid region bounded by $x + 2y + 3z = 6$ and the coordinate planes and has density $\rho (x,y,z) = x^2 yz$. Find the total mass.

Solution

The region $Q$ is a tetrahedron (Figure $\PageIndex{7}$) meeting the axes at the points $(6,0,0), \, (0,3,0),$ and $(0,0,2)$. To find the limits of integration, let $z = 0$ in the slanted plane $z = \dfrac{1}{3} (6 - x - 2y)$. Then for $x$ and $y$ find the projection of $Q$ onto the $xy$-plane, which is bounded by the axes and the line $x + 2y = 6$. Hence the mass is

$$m = \iiint_Q \rho (x,y,z) dV = \int_{x=0}^{x=6} \int_{y=0}^{y=1/2(6-x)} \int_{z=0}^{z=1/3(6-x-2y)} x^2 yz \, dz \, dy \, dx = \dfrac{108}{35}$$

Figure $\PageIndex{7}$: Finding the mass of a three-dimensional solid $Q$.

Exercise $\PageIndex{8}$

Consider the same region $Q$ (Figure $\PageIndex{7}$), and use the density function $\rho (x,y,z) = xy^2z$. Find the mass.

Hint

Follow the steps in the previous example.

Answer

$\dfrac{54}{35} = 1.543$

Example $\PageIndex{9}$: Finding the Center of Mass of a Solid

Suppose $Q$ is a solid region bounded by the plane $x + 2y + 3z = 6$ and the coordinate planes with density $\rho (x,y,z) = x^2yz$ (see Figure $\PageIndex{7}$). Find the center of mass using decimal approximation.

Solution

We have used this tetrahedron before and know the limits of integration, so we can proceed to the computations right away. First, we need to find the moments about the $xy$-plane, the $xz$-plane, and the $yz$-plane:

$$M_{xy} = \iiint_Q z\rho (x,y,z) dV = \int_{x=0}^{x=6} \int_{y=0}^{y=1/2(6-x)} \int_{z=0}^{z=1/3(6-x-2y)} x^2 yz^2 dz \, dy \, dx = \dfrac{54}{35} \approx 1.543,$$

$$M_{xz} = \iiint_Q y\rho (x,y,z) dV = \int_{x=0}^{x=6} \int_{y=0}^{y=1/2(6-x)} \int_{z=0}^{z=1/3(6-x-2y)} x^2 y^2z \, dz \, dy \, dx = \dfrac{81}{35} \approx 2.314,$$

$$M_{yz} = \iiint_Q x\rho (x,y,z) dV = \int_{x=0}^{x=6} \int_{y=0}^{y=1/2(6-x)} \int_{z=0}^{z=1/3(6-x-2y)} x^3 yz \, dz \, dy \, dx = \dfrac{243}{35} \approx 6.943.$$

Hence the center of mass is

$$\bar{x} = \dfrac{M_{yz}}{m}, \, \bar{y} = \dfrac{M_{xz}}{m}, \, \bar{z} = \dfrac{M_{xy}}{m},$$

$$\bar{x} = \dfrac{M_{yz}}{m} = \dfrac{243/35}{108/35} = \dfrac{243}{108} = 2.25,$$

$$\bar{y} = \dfrac{M_{xz}}{m} = \dfrac{81/35}{108/35} = \dfrac{81}{108} = 0.75,$$

$$\bar{z} = \dfrac{M_{xy}}{m} = \dfrac{54/35}{108/35} = \dfrac{54}{108} = 0.5$$

The center of mass for the tetrahedron $Q$ is the point $(2.25, 0.75, 0.5)$.

Exercise $\PageIndex{9}$

Consider the same region $Q$ (Figure $\PageIndex{7}$) and use the density function $\rho (x,y,z) = xy^2z$. Find the center of mass.

Hint

Check that $M_{xy} = \dfrac{27}{35}, \, M_{xz} = \dfrac{243}{140},$ and $M_{yz} = \dfrac{81}{35}$. Then use $m$ from a previous checkpoint question.

Answer

$\left(\dfrac{3}{2}, \dfrac{9}{8}, \dfrac{1}{2}\right)$

We conclude this section with an example of finding moments of inertia $I_x, \, I_y$, and $I_z$.

Example $\PageIndex{10}$: Finding the Moments of Inertia of a Solid

Suppose that $Q$ is a solid region and is bounded by $x + 2y + 3z = 6$ and the coordinate planes with density $\rho (x,y,z) = x^2 yz$ (see Figure $\PageIndex{7}$). Find the moments of inertia of the tetrahedron $Q$ about the $yz$-plane, the $xz$-plane, and the $xy$-plane.

Solution

Once again, we can almost immediately write the limits of integration and hence we can quickly proceed to evaluating the moments of inertia. Using the formula stated before, the moments of inertia of the tetrahedron $Q$ about the $yz$-plane, the $xz$-plane, and the $xy$-plane are

$$I_x = \iiint_Q (y^2 + z^2) \rho(x,y,z) dV,$$

$$I_y = \iiint_Q (x^2 + z^2) \rho(x,y,z) dV,$$ and

$$I_z = \iiint_Q (x^2 + y^2) \rho(x,y,z) dV \, with \, \rho(x,y,z) = x^2yz.$$

Proceeding with the computations, we have

$$\begin{align*} I_x &= \iiint_Q (y^2 + z^2) x^2 \rho(x,y,z) dV \\[5pt] &= \int_{x=0}^{x=6} \int_{y=0}^{y=\dfrac{1}{2}(6-x)} \int_{z=0}^{z=\dfrac{1}{3}(6-x-2y)} (y^2 + z^2) x^2 yz \, dz \, dy \, dx = \dfrac{117}{35} \approx 3.343,\end{align*}$$

$$\begin{align*} I_y &= \iiint_Q (x^2 + z^2) x^2 \rho(x,y,z) dV \\[5pt] &= \int_{x=0}^{x=6} \int_{y=0}^{y=\dfrac{1}{2}(6-x)} \int_{z=0}^{z=\dfrac{1}{3}(6-x-2y)} (x^2 + z^2) x^2 yz \, dz \, dy \, dx = \dfrac{684}{35} \approx 19.543, \end{align*}$$

$$\begin{align*} I_z &= \iiint_Q (x^2 + y^2) x^2 \rho(x,y,z) dV \\[5pt] &= \int_{x=0}^{x=6} \int_{y=0}^{y=\dfrac{1}{2}(6-x)} \int_{z=0}^{z=\dfrac{1}{3}(6-x-2y)} (x^2 + y^2) x^2 yz \, dz \, dy \, dx = \dfrac{729}{35} \approx 20.829. \end{align*}$$

Thus, the moments of inertia of the tetrahedron $Q$ about the $yz$-plane, the $xz$-plane, and the $xy$-plane are $117/35, \, 684/35$, and $729/35$, respectively.

Exercise $\PageIndex{10}$

Consider the same region $Q$ (Figure $\PageIndex{7}$), and use the density function $\rho(x,y,z) = xy^2z$. Find the moments of inertia about the three coordinate planes.

Answer

The moments of inertia of the tetrahedron $Q$ about the $yz$-plane, the $xz$-plane, and the $xy$-plane are $99/35, \, 36/7$ and $243/35$, respectively.

Key Concepts

Finding the mass, center of mass, moments, and moments of inertia in double integrals:

• For a lamina $R$ with a density function $\rho (x,y)$ at any point $(x,y)$ in the plane, the mass is $$m = \iint_R \rho (x,y)dA.$$
• The moments about the $x$-axis and $y$-axis are $$M_x = \iint_R y\rho(x,y) dA \, and \, M_y = \iint_R x\rho(x,y)dA.$$
• The center of mass is given by $\bar{x} = \dfrac{M_y}{m}, \, \bar{y} = \dfrac{M_x}{m}$.
• The center of mass becomes the centroid of the plane when the density is constant.
• The moments of inertia about the $x$-axis, $y$-axis, and the origin are $$I_x = \iint_R y^2 \rho(x,y) dA, \, I_y = \iint_R x^2 \rho(x,y) dA, \, and \, I_0 = I_x + I_y = \iint_R (x^2 + y^2) \rho(x,y) dA.$$

Finding the mass, center of mass, moments, and moments of inertia in triple integrals:

• For a solid object $Q$ with a density function $\rho(x,y,z)$ at any point $(x,y,z)$ in space, the mass is $$m = \iiint_Q \rho (x,y,z) dV.$$
• The moments about the $xy$-plane, the $xz$-plane, and the $yz$-plane are $$M_{xy} = \iiint_Q z\rho (x,y,z)dV, \, M_{xz} = \iiint_Q y\rho (x,y,z)dV, \, M_{yz} = \iiint_Q x\rho (x,y,z)dV$$
• The center of mass is given by $\bar{x} = \dfrac{M_{yz}}{m}, \, \bar{y} = \dfrac{M_{xz}}{m}, \, \bar{z} = \dfrac{M_{xy}}{m}.$
• The center of mass becomes the centroid of the solid when the density is constant.
• The moments of inertia about the $yz$-plane, the $xz$-plane, and the $xy$-plane are $$I_x = \iiint_Q (y^2 + z^2) \, \rho (x,y,z) \, dV, \, I_y = \iiint_Q (x^2 + z^2) \, \rho (x,y,z) \, dV, \, I_z = \iiint_Q (x^2 + y^2) \, \rho (x,y,z) \, dV.$$

Key Equations

• Mass of a lamina $$m = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l m_{ij} = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l \rho (x_{ij}^8, y_{ij}^*) \Delta A = \iint_R \rho(x,y) dA$$
• Moment about the x-axis $$M_x = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*) m_{ij} = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*) \rho (x_{ij}^8, y_{ij}^*) \Delta A = \iint_R y\rho(x,y)dA$$
• Moment about the y-axis $$M_y = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*) m_{ij} = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*) \rho (x_{ij}^8, y_{ij}^*) \Delta A = \iint_R x\rho(x,y)dA$$
• Center of mass of a lamina $$\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x\rho (x,y) dA}{\iint_R \rho (x,y) dA} \, and \, \bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y\rho (x,y) dA}{\iint_R \rho (x,y) dA}$$

Glossary

radius of gyration

the distance from an object’s center of mass to its axis of rotation

Contributors and Attributions

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.