9.6: Surface Integrals
( \newcommand{\kernel}{\mathrm{null}\,}\)
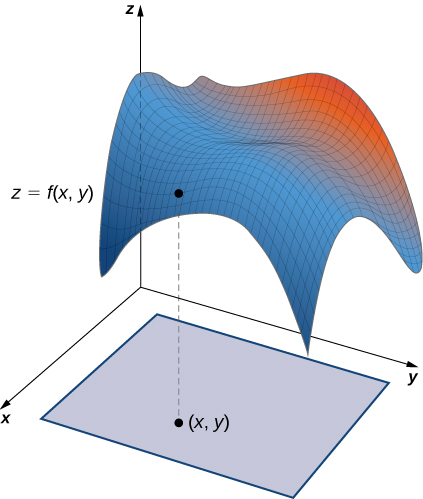
We have seen that a line integral is an integral over a path in a plane or in space. However, if we wish to integrate over a surface (a two-dimensional object) rather than a path (a one-dimensional object) in space, then we need a new kind of integral that can handle integration over objects in higher dimensions. We can extend the concept of a line integral to a surface integral to allow us to perform this integration.
Surface integrals are important for the same reasons that line integrals are important. They have many applications to physics and engineering, and they allow us to develop higher dimensional versions of the Fundamental Theorem of Calculus. In particular, surface integrals allow us to generalize Green’s theorem to higher dimensions, and they appear in some important theorems we discuss in later sections.
Parametric Surfaces
A surface integral is similar to a line integral, except the integration is done over a surface rather than a path. In this sense, surface integrals expand on our study of line integrals. Just as with line integrals, there are two kinds of surface integrals: a surface integral of a scalar-valued function and a surface integral of a vector field.
However, before we can integrate over a surface, we need to consider the surface itself. Recall that to calculate a scalar or vector line integral over curve
A parameterized surface is given by a description of the form
Notice that this parameterization involves two parameters,
Definition: Parameter Domain
Given a parameterization of surface
the parameter domain of the parameterization is the set of points in the
Example
Describe surface
Solution
To get an idea of the shape of the surface, we first plot some points. Since the parameter domain is all of
Although plotting points may give us an idea of the shape of the surface, we usually need quite a few points to see the shape. Since it is time-consuming to plot dozens or hundreds of points, we use another strategy. To visualize
- Suppose that
- Suppose that
If
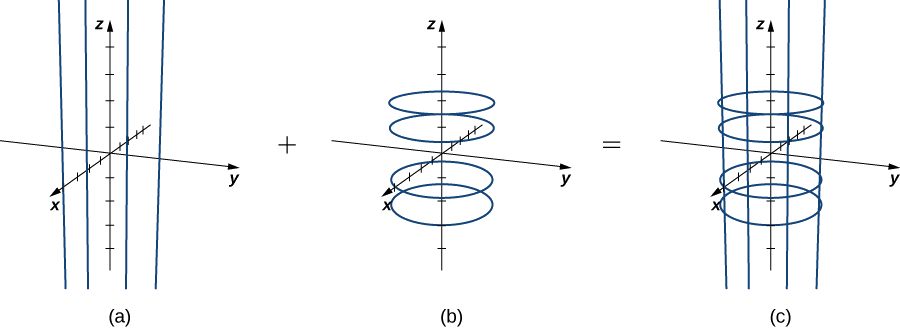
Notice that if
Analysis
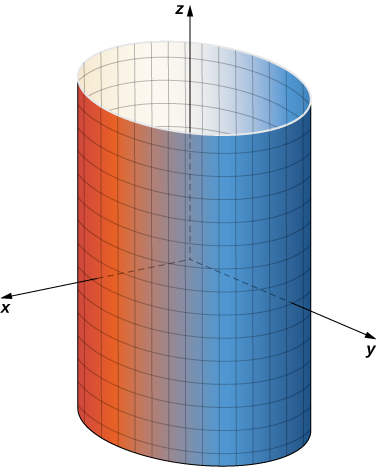
Notice that if we change the parameter domain, we could get a different surface. For example, if we restricted the domain to
Exercise
Describe the surface with parameterization
- Hint
-
Hold
- Answer
-
Cylinder
Example
Give a parameterization of the cone
Solution
The horizontal cross-section of the cone at height
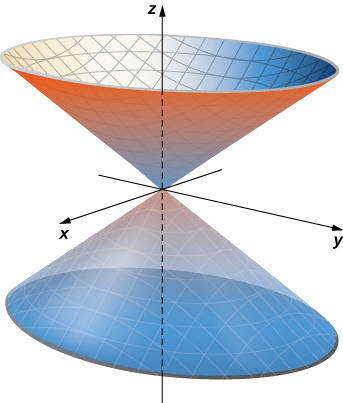
Exercise
Give a parameterization for the portion of cone
- Hint
-
Consider the parameter domain for this surface.
- Answer
-
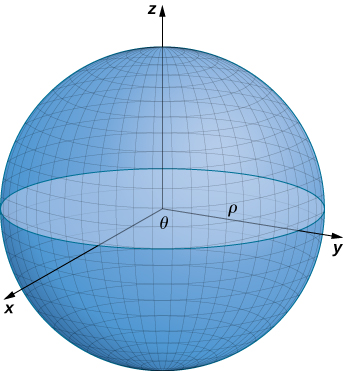
We have discussed parameterizations of various surfaces, but two important types of surfaces need a separate discussion: spheres and graphs of two-variable functions. To parameterize a sphere, it is easiest to use spherical coordinates. The sphere of radius
The idea of this parameterization is that as
This results in the desired circle (Figure
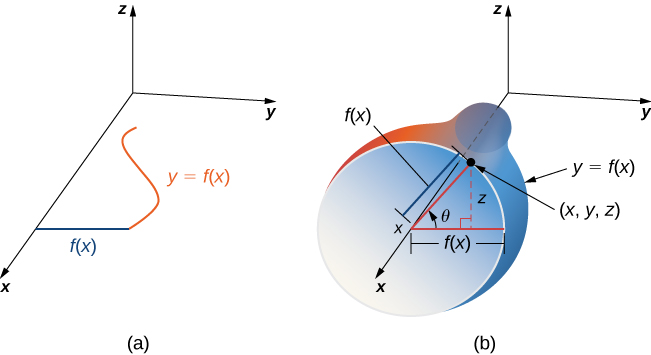
Finally, to parameterize the graph of a two-variable function, we first let
Similarly, if
Let’s now generalize the notions of smoothness and regularity to a parametric surface. Recall that curve parameterization
Analogously, we would like a notion of regularity (or smoothness) for surfaces so that a surface parameterization really does trace out a surface. To motivate the definition of regularity of a surface parameterization, consider the parameterization
Although this parameterization appears to be the parameterization of a surface, notice that the image is actually a line (Figure

DEFINITION: regular parameterization
Parameterization
If parameterization
Recall that curve parameterization
DEFINITION: Smooth Surfaces
A surface parameterization
A surface may also be piecewise smooth if it has smooth faces but also has locations where the directional derivatives do not exist.
Example
Which of the figures in Figure

Solution
The surface in Figure
(we can use technology to verify). Notice that vectors
and
exist for any choice of
The
In the pyramid in Figure
Exercise
Is the surface parameterization
- Hint
-
Investigate the cross product
- Answer
-
Yes
Surface Area of a Parametric Surface
Our goal is to define a surface integral, and as a first step we have examined how to parameterize a surface. The second step is to define the surface area of a parametric surface. The notation needed to develop this definition is used throughout the rest of this chapter.
Let
Note that we can form a grid with lines that are parallel to the
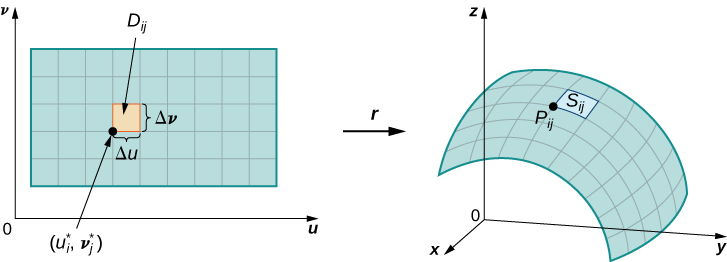
Now consider the vectors that are tangent to these grid curves. For grid curve
For grid curve
If vector
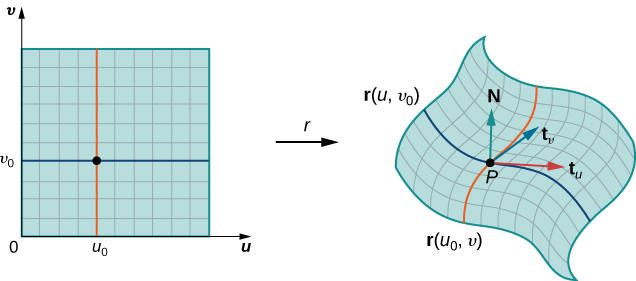
The tangent plane at
Varying point
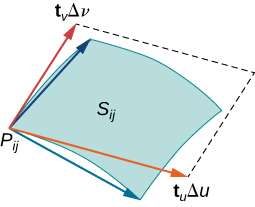
definition: smooth parameterization of surface
Let
where
and
Example
Calculate the lateral surface area (the area of the “side,” not including the base) of the right circular cone with height h and radius r.
Solution
Before calculating the surface area of this cone using Equation
The idea behind this parameterization is that for a fixed
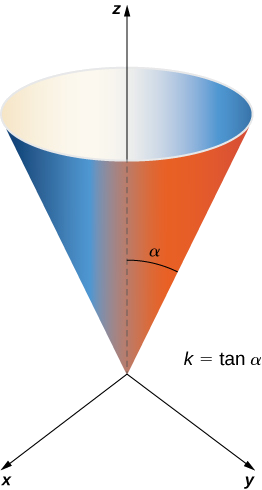
With a parameterization in hand, we can calculate the surface area of the cone using Equation
The magnitude of this vector is
By Equation
Since
Therefore, the lateral surface area of the cone is
The surface area of a right circular cone with radius
Exercise
Find the surface area of the surface with parameterization
- Hint
-
Use Equation
- Answer
-
Example
Show that the surface area of the sphere
Solution
The sphere has parameterization
The tangent vectors are
and
Therefore,
Now,
Notice that
We have derived the familiar formula for the surface area of a sphere using surface integrals.
Exercise
Show that the surface area of cylinder
- Hint
-
Use the standard parameterization of a cylinder and follow the previous example.
- Answer
-
With the standard parameterization of a cylinder, Equation
In addition to parameterizing surfaces given by equations or standard geometric shapes such as cones and spheres, we can also parameterize surfaces of revolution. Therefore, we can calculate the surface area of a surface of revolution by using the same techniques. Let
Example
Find the area of the surface of revolution obtained by rotating
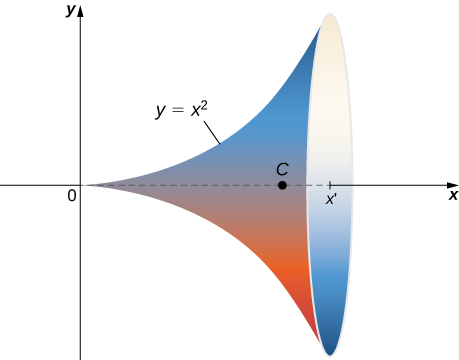
Solution
This surface has parameterizationThe tangent vectors are
Therefore,
and
The area of the surface of revolution is
Exercise
Use Equation
- Hint
-
Use the parameterization of surfaces of revolution given before Example
- Answer
-
Surface Integral of a Scalar-Valued Function
Now that we can parameterize surfaces and we can calculate their surface areas, we are able to define surface integrals. First, let’s look at the surface integral of a scalar-valued function. Informally, the surface integral of a scalar-valued function is an analog of a scalar line integral in one higher dimension. The domain of integration of a scalar line integral is a parameterized curve (a one-dimensional object); the domain of integration of a scalar surface integral is a parameterized surface (a two-dimensional object). Therefore, the definition of a surface integral follows the definition of a line integral quite closely. For scalar line integrals, we chopped the domain curve into tiny pieces, chose a point in each piece, computed the function at that point, and took a limit of the corresponding Riemann sum. For scalar surface integrals, we chop the domain region (no longer a curve) into tiny pieces and proceed in the same fashion.
Let
To define a surface integral of a scalar-valued function, we let the areas of the pieces of
DEFINITION: surface integral of a scalar-valued function
The surface integral of a scalar-valued function of
Again, notice the similarities between this definition and the definition of a scalar line integral. In the definition of a line integral we chop a curve into pieces, evaluate a function at a point in each piece, and let the length of the pieces shrink to zero by taking the limit of the corresponding Riemann sum. In the definition of a surface integral, we chop a surface into pieces, evaluate a function at a point in each piece, and let the area of the pieces shrink to zero by taking the limit of the corresponding Riemann sum. Thus, a surface integral is similar to a line integral but in one higher dimension.
The definition of a scalar line integral can be extended to parameter domains that are not rectangles by using the same logic used earlier. The basic idea is to chop the parameter domain into small pieces, choose a sample point in each piece, and so on. The exact shape of each piece in the sample domain becomes irrelevant as the areas of the pieces shrink to zero.
Scalar surface integrals are difficult to compute from the definition, just as scalar line integrals are. To develop a method that makes surface integrals easier to compute, we approximate surface areas
From the material we have already studied, we know that
Therefore,
This approximation becomes arbitrarily close to
Equation
In this case, vector
Example
Calculate surface integral
Solution
Notice that this parameter domain
To use Equation to calculate the surface integral, we first find vectors
By Equation,
Example
Calculate surface integral
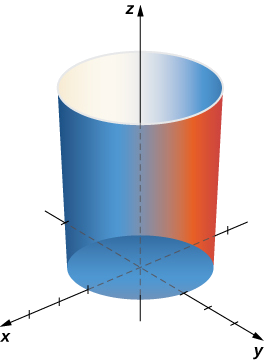
Solution
To calculate the surface integral, we first need a parameterization of the cylinder. Following Example, a parameterization is
The tangent vectors are
and
Example
Calculate surface integral
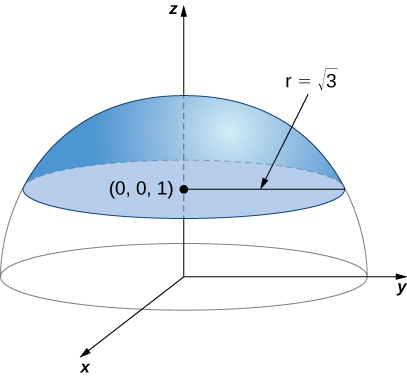
Solution
Notice that
First, we calculate
Therefore, the radius of the disk is
The magnitude of this vector is
Now we calculate
Since we are only taking the piece of the sphere on or above plane
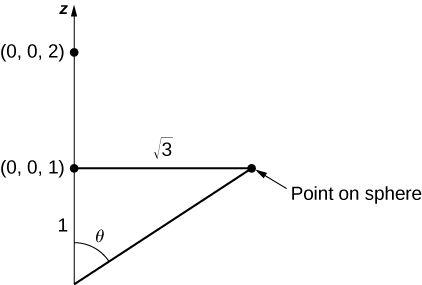
The tangent vectors are
The magnitude of this vector is
Therefore,
Since
Analysis
In this example we broke a surface integral over a piecewise surface into the addition of surface integrals over smooth subsurfaces. There were only two smooth subsurfaces in this example, but this technique extends to finitely many smooth subsurfaces.
Exercise
Calculate line integral
- Hint
-
Break the integral into three separate surface integrals.
- Answer
-
0
Scalar surface integrals have several real-world applications. Recall that scalar line integrals can be used to compute the mass of a wire given its density function. In a similar fashion, we can use scalar surface integrals to compute the mass of a sheet given its density function. If a thin sheet of metal has the shape of surface S and the density of the sheet at point
Example
A flat sheet of metal has the shape of surface
Solution
Let
The tangent vectors are
By the definition of the line integral (Section 16.2),
Exercise
A piece of metal has a shape that is modeled by paraboloid
- Hint
-
The mass of a sheet is given by
- Answer
-
Orientation of a Surface
Recall that when we defined a scalar line integral, we did not need to worry about an orientation of the curve of integration. The same was true for scalar surface integrals: we did not need to worry about an “orientation” of the surface of integration.
On the other hand, when we defined vector line integrals, the curve of integration needed an orientation. That is, we needed the notion of an oriented curve to define a vector line integral without ambiguity. Similarly, when we define a surface integral of a vector field, we need the notion of an oriented surface. An oriented surface is given an “upward” or “downward” orientation or, in the case of surfaces such as a sphere or cylinder, an “outward” or “inward” orientation.
Let S be a smooth surface. For any point
Closed surfaces such as spheres are orientable: if we choose the outward normal vector at each point on the surface of the sphere, then the unit normal vectors vary continuously. This is called the positive orientation of the closed surface (Figure). We also could choose the inward normal vector at each point to give an “inward” orientation, which is the negative orientation of the surface.
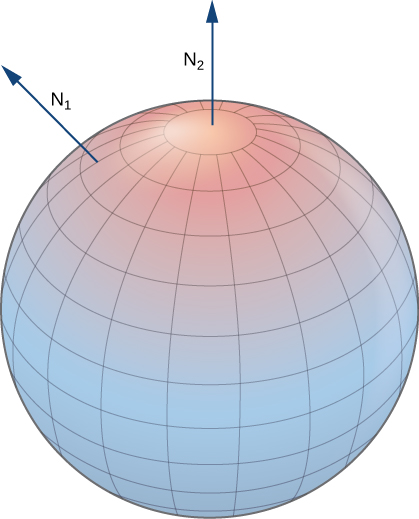
A portion of the graph of any smooth function
Let
gives an orientation of surface
Example
Give an orientation of cylinder
Solution
This surface has parameterization
The tangent vectors are
In this case,
An orientation of the cylinder is
Notice that all vectors are parallel to the
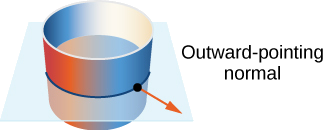
Exercise
Give the “upward” orientation of the graph of
- Hint
-
Parameterize the surface and use the fact that the surface is the graph of a function.
- Answer
-
Since every curve has a “forward” and “backward” direction (or, in the case of a closed curve, a clockwise and counterclockwise direction), it is possible to give an orientation to any curve. Hence, it is possible to think of every curve as an oriented curve. This is not the case with surfaces, however. Some surfaces cannot be oriented; such surfaces are called nonorientable. Essentially, a surface can be oriented if the surface has an “inner” side and an “outer” side, or an “upward” side and a “downward” side. Some surfaces are twisted in such a fashion that there is no well-defined notion of an “inner” or “outer” side.
The classic example of a nonorientable surface is the Möbius strip. To create a Möbius strip, take a rectangular strip of paper, give the piece of paper a half-twist, and the glue the ends together (Figure

Since some surfaces are nonorientable, it is not possible to define a vector surface integral on all piecewise smooth surfaces. This is in contrast to vector line integrals, which can be defined on any piecewise smooth curve.
Surface Integral of a Vector Field
With the idea of orientable surfaces in place, we are now ready to define a surface integral of a vector field. The definition is analogous to the definition of the flux of a vector field along a plane curve. Recall that if
To place this definition in a real-world setting, let
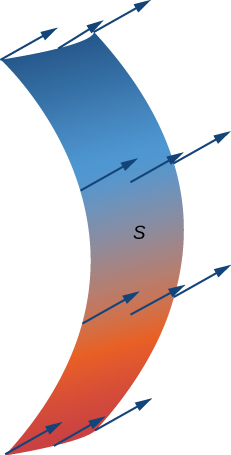
The rate of flow, measured in mass per unit time per unit area, is
As pieces
gets arbitrarily close to the mass flux. Therefore, the mass flux is
This is a surface integral of a vector field. Letting the vector field

Definition: Surface Integrals
Let
Notice the parallel between this definition and the definition of vector line integral
Just as with vector line integrals, surface integral
Therefore, to compute a surface integral over a vector field we can use the equation
Example
Calculate the surface integral
Solution
The tangent vectors are
By Equation
Therefore, the flux of
Exercise
Calculate surface integral
- Hint
-
Use Equation
- Answer
-
0
Example
Let
Solution
A parameterization of the surface is
As in Example, the tangent vectors are
Notice that each component of the cross product is positive, and therefore this vector gives the outward orientation. Therefore we use the orientation
for the sphere.
By Equation,
Therefore, the mass flow rate is
Exercise
Let
- Hint
-
Use Equation.
- Answer
-
400 kg/sec/m
In Example
which leaves out the density. Since the flow rate of a fluid is measured in volume per unit time, flow rate does not take mass into account. Therefore, we have the following characterization of the flow rate of a fluid with velocity
Flow rate of fluid across
To compute the flow rate of the fluid in Example, we simply remove the density constant, which gives a flow rate of
Both mass flux and flow rate are important in physics and engineering. Mass flux measures how much mass is flowing across a surface; flow rate measures how much volume of fluid is flowing across a surface.
In addition to modeling fluid flow, surface integrals can be used to model heat flow. Suppose that the temperature at point
Example
A cast-iron solid cylinder is given by inequalities
Solution
Let
First we consider the circular bottom of the object, which we denote
Therefore,
Since the surface is oriented outward and
Now let’s consider the circular top of the object, which we denote
Therefore,
Since the surface is oriented outward and
Last, let’s consider the cylindrical side of the object. This surface has parameterization
Therefore, the rate of heat flow across
Exercise
A cast-iron solid ball is given by inequality
- Hint
-
Follow the steps of Example
- Answer
-
Key Concepts
- Surfaces can be parameterized, just as curves can be parameterized. In general, surfaces must be parameterized with two parameters.
- Surfaces can sometimes be oriented, just as curves can be oriented. Some surfaces, such as a Möbius strip, cannot be oriented.
- A surface integral is like a line integral in one higher dimension. The domain of integration of a surface integral is a surface in a plane or space, rather than a curve in a plane or space.
- The integrand of a surface integral can be a scalar function or a vector field. To calculate a surface integral with an integrand that is a function, use Equation. To calculate a surface integral with an integrand that is a vector field, use Equation.
- If
Key Equations
- Scalar surface integral
- Flux integral
Glossary
- flux integral
- another name for a surface integral of a vector field; the preferred term in physics and engineering
- grid curves
- curves on a surface that are parallel to grid lines in a coordinate plane
- heat flow
- a vector field proportional to the negative temperature gradient in an object
- mass flux
- the rate of mass flow of a fluid per unit area, measured in mass per unit time per unit area
- orientation of a surface
- if a surface has an “inner” side and an “outer” side, then an orientation is a choice of the inner or the outer side; the surface could also have “upward” and “downward” orientations
- parameter domain (parameter space)
- the region of the
- parameterized surface (parametric surface)
- a surface given by a description of the form
- regular parameterization
- parameterization
- surface area
- the area of surface
- surface integral
- an integral of a function over a surface
- surface integral of a scalar-valued function
- a surface integral in which the integrand is a scalar function
- surface integral of a vector field
- a surface integral in which the integrand is a vector field
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.



It follows from Example
We can also find different types of surfaces given their parameterization, or we can find a parameterization when we are given a surface.
Example
Describe surface
Solution
Notice that if
Therefore, the surface is the elliptic paraboloid
Exercise
Describe the surface parameterized by
Hold
Cone