9.6E: Exercises

Last updated
Save as PDF

Page ID: 26277

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Exercise $\PageIndex{1}$: True or false.

For the following exercises, determine whether the statements are true or false.

1. If surface S is given by $\{(x,y,z) : \, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, z = 10 \}$, then \[\iint_S f(x,y,z) \, dS = \int_0^1 \int_0^1 f (x,y,10) \, dx dy.\]

Answer: True

2. If surface S is given by $\{(x,y,z) : \, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, z = x \}$, then \[\iint_S f(x,y,z) \, dS = \int_0^1 \int_0^1 f (x,y,x) \, dx dy.\]

3. Surface $r = \langle v \, \cos u, \, v \, \sin u, \, v^2 \rangle, \, for \, 0 \leq u \leq \pi, \, 0 \leq v \leq 2$ is the same surface $r = \langle \sqrt{v} \, \cos 2u, \, \sqrt{v} \, \sin 2u, \, v \rangle, \, for \, 0 \leq u \leq \dfrac{\pi}{2}, \, 0 \leq v \leq 4$.

Answer: True

Exercise $\PageIndex{2}$

Given the standard parameterization of a sphere, normal vectors $t_u \times t_v$ are outward normal vectors. For the following exercises, find parametric descriptions for the following surfaces.

1. Plane $3x - 2y + z = 2$

Answer: $r(u,v) = \langle u, \, v, \, 2 - 3u + 2v \rangle $ for $-\infty \leq u < \infty$ and $ - \infty \leq v < \infty$.

2. Paraboloid $z = x^2 + y^2$, for $0 \leq z \leq 9$.

3. Plane $2x - 4y + 3z = 16$

Answer: $r(u,v) = \langle u, \, v, \, \dfrac{1}{3} (16 - 2u + 4v) \rangle $ for $|u| < \infty$ and $|v| < \infty$.

4. The frustum of cone $z^2 = x^2 + y^2$, for $2 \leq z \leq 8$

5. The portion of cylinder $x^2 + y^2 = 9$ in the first octant, for $0 \leq z \leq 3$

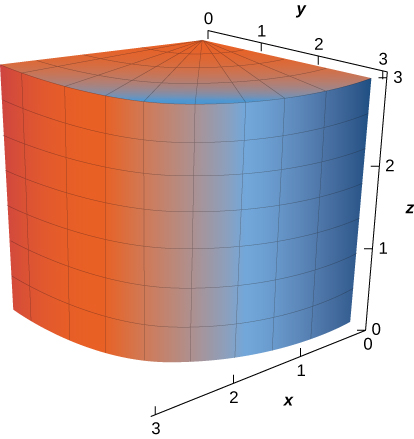
$A diagram in three dimensions of a section of a cylinder with radius 3. The center of its circular top is (0,0,3). The section exists for x, y, and z between 0 and 3.$

Answer: $r(u,v) = \langle 3 \, \cos u, \, 3 \, \sin u, \, v \rangle $ for $0 \leq u \leq \dfrac{\pi}{2}, \, 0 \leq v \leq 3$

6. A cone with base radius r and height h, where r and h are positive constants

Answer: TBA

Exercise $\PageIndex{3}$: Surface Area

For the following exercises, use a computer algebra system to approximate the area of the following surfaces using a parametric description of the surface.

1. [T] Half cylinder $\{ (r, \theta, z) : \, r = 4, \, 0 \leq \theta \leq \pi, \, 0 \leq z \leq 7 \}$

Answer: $A = 87.9646$

2. [T] Plane $z = 10 - z - y$ above square $|x| \leq 2, \, |y| \leq 2$

Exercise $\PageIndex{4}$

For the following exercises, let S be the hemisphere $x^2 + y^2 + z^2 = 4$, with $z \geq 0$, and evaluate each surface integral, in the counterclockwise direction.

1. \[\iint_S z\, dS\]

Answer: \[\iint_S z \, dS = 8\pi\]

2. \[\iint_S (x - 2y) \, dS\]

3. \[\iint_S (x^2 + y^2) \, dS\]

Answer: \[\iint_S z \, dS = 8\pi\]

Exercise $\PageIndex{5}$

For the following exercises, evaluate \[\int \int_S \vecs{F} \cdot \vecs{N} \, ds\] for vector field $\vecs{F}$, where $\vecs{N}$ is an outward normal vector to surface S.

1. $\vecs{F}(x,y,z) = x \, \hat{ \mathbf i} + 2y\, \hat{ \mathbf j} + 3z\, \hat{ \mathbf k} $, and S is that part of plane $15x - 12y + 3z = 6$ that lies above unit square $0 \leq x \leq 1, \, 0 \leq y \leq 1$.

2. $\vecs{F}(x,y) = x\, \hat{ \mathbf i} + y\, \hat{ \mathbf j} $, and S is hemisphere $z = \sqrt{1 - x^2 - y^2}$.

Answer: \[\iint_S F \cdot N \, dS = \dfrac{4\pi}{3}\]

3. $F(x,y,z) = x^2 \, \hat{ \mathbf i} + y^2 \, \hat{ \mathbf j} + z^2 \, \hat{ \mathbf k} $, and S is the portion of plane $z = y + 1$ that lies inside cylinder $x^2 + y^2 = 1$.

A cylinder and an intersecting plane shown in three-dimensions. S is the portion of the plane z = y + 1 inside the cylinder x^2 + y ^2 = 1.

Exercise $\PageIndex{6}$

For the following exercises, approximate the mass of the homogeneous lamina that has the shape of given surface S. Round to four decimal places.

1. [T] S is surface $z = 4 - x - 2y$, with $z \geq 0, \, x \geq 0, \, y \geq 0; \xi=x.$

Answer: $m \approx 13.0639$

2. [T] S is surface $z = x^2 + y^2$, with $z \leq 1; \, \xi = z$.

3. [T] S is surface $x^2 + y^2 + x^2 = 5$, with $z \geq 1; \, \xi = \theta^2$.

Answer: $m \approx 228.5313$

Exercise $\PageIndex{6}$

1. Evaluate \[\iint_S (y^2 z\, \hat{ \mathbf i} + y^3\, \hat{ \mathbf j}+ xz\, \hat{ \mathbf k}) \cdot dS,\] where S is the surface of cube $-1 \leq x \leq 1, \, -1 \leq y \leq 1$, and $0 \leq z \leq 2$ in a counterclockwise direction.

2. Evaluate surface integral \[\iint_S gdS,\] where $g(x,y,z) = xz + 2x^2 - 3xy$ and S is the portion of plane $2x - 3y + z = 6$ that lies over unit square R: $0 \leq x \leq 1, \, 0 \leq y \leq 1$.

Answer: \[\iint_S gdS = 3 \sqrt{4}\]

3. Evaluate \[\iint_S (x + y + z)dS,\] where S is the surface defined parametrically by $R(u,v) = (2u + v)\, \hat{ \mathbf i} + (u - 2v)\, \hat{ \mathbf j} + (u + 3v)\, \hat{ \mathbf k}$ for $0 \leq u \leq 1$, and $0 \leq v \leq 2$.

$A three-dimensional diagram of the given surface, which appears to be a steeply sloped plane stretching through the (x,y) plane.$

Answer: TBA

Exercise $\PageIndex{7}$

1. [T] Evaluate \[\iint_S (x - y^2 + z)dS,\] where S is the surface defined parametrically by $R(u,v) = u^2\, \hat{ \mathbf i} + v\, \hat{ \mathbf j} + u\, \hat{ \mathbf k}$ for $0 \leq u \leq 1, \, 0 \leq v \leq 1$.

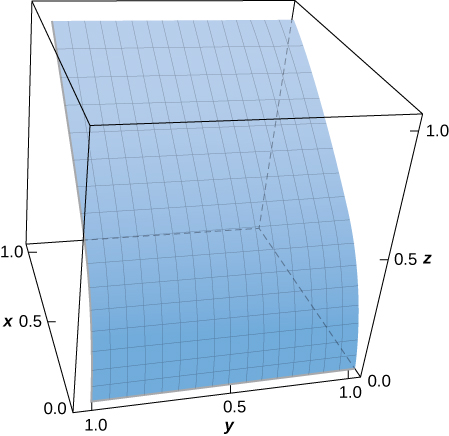
$A three-dimensional diagram of the given surface, which appears to be a curve with edges parallel to the y-axis. It increases in x components and decreases in z components the further it is from the y axis.$

Answer: \[\iint_S (x^2 + y - z) \, dS \approx 0.9617\]

2. [T] Evaluate where S is the surface defined by $R(u,v) = u \, \hat{ \mathbf i} - u^2 \, \hat{ \mathbf j}+ v\, \hat{ \mathbf k}, \, 0 \leq u \leq 2, \, 0 \leq v \leq 1$ for $0 \leq u \leq 1, \, 0 \leq v \leq 2$.

3. Evaluate \[ \iint_S (x^2 + y^2) \, dS,\] where S is the surface bounded above hemisphere $z = \sqrt{1 - x^2 - y^2}$, and below by plane $z = 0$.

Answer: \[\iint_S (x^2 + y^2) \, dS = \dfrac{4\pi}{3}\]

4. Evaluate \[ \iint_S (x^2 + y^2 + z^2) \, dS,\] where S is the portion of plane that lies inside cylinder $x^2 + y^2 = 1$.

5. [T] Evaluate \[\iint_S x^2 z dS,\] where S is the portion of cone $z^2 = x^2 + y^2$ that lies between planes $z = 1$ and $z = 4$.

A diagram of the given upward opening cone in three dimensions. The cone is cut by planes z=1 and z=4.

Answer: \[\iint_S x^2 zdS = \dfrac{1023\sqrt{2\pi}}{5}\]

6. [T] Evaluate \[\iint_S (xz/y) \, dS,\] where S is the portion of cylinder $x = y^2$ that lies in the first octant between planes $z = 0, \, z = 5$, and $y = 4$.

A diagram of the given cylinder in three-dimensions. It is cut by the planes z=0, z=5, y=1, and y=4.

7. [T] Evaluate \[\iint_S (z + y) \, dS,\] where S is the part of the graph of $ z = \sqrt{1 - x^2}$ in the first octant between the xz-plane and plane $y = 3$.

A diagram of the given surface in three dimensions in the first octant between the xz-plane and plane y=3. The given graph of z= the square root of (1-x^2) stretches down in a concave down curve from along (0,y,1) to along (1,y,0). It looks like a portion of a horizontal cylinder with base along the xz-plane and height along the y axis.

Answer: \[\iint_S (z + y) \, dS \approx 10.1\]

Exercise $\PageIndex{8}$

1. Evaluate \[\iint_S xyz\, dS\] if S is the part of plane $z = x + y$ that lies over the triangular region in the xy-plane with vertices (0, 0, 0), (1, 0, 0), and (0, 2, 0).

2. Find the mass of a lamina of density $\xi (x,y,z) = z$ in the shape of hemisphere $z = (a^2 - x^2 - y^2)^{1/2}$.

Answer: $m = \pi a^3$

3. Compute \[\int \int_S F \cdot N \, dS,\] where $F(x,y,z) = x \, \hat{ \mathbf i} - 5y \hat{j]+ 4z\, \hat{ \mathbf k}$ and $\vecs{N}$ is an outward normal vector S, where S is the union of two squares $S_1$ : $x = 0, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1$ and $S_2 \, : \, x = 0, \, 0 \leq x \leq 1, \, 0 \leq y \leq 1$.

A diagram in three dimensions. It shows the square formed by the components x=0, 0 <= y <= 1, and 0 <= z <= 1. It also shows the square formed by the components z=1, 0 <= x <= 1, and 0 <= y <= 1.

4. Compute \[\int \int_S F \cdot N \, dS,\] where $F(x,y,z) = xy \, \hat{ \mathbf i} + z\, \hat{ \mathbf j} + (x + y) \, \hat{ \mathbf k}$ and $\vecs{N}$ is an outward normal vector S, where S is the triangular region cut off from plane $x + y + z = 1$ by the positive coordinate axes.

Answer: \[\iint_S F \cdot N \, dS = \dfrac{13}{24}\]

Exercise $\PageIndex{9}$

Compute \[\int \int_S F \cdot N \, dS,\] where $F(x,y,z) = 2yz\, \hat{ \mathbf i}+ (tan^{-1}xz)\, \hat{ \mathbf j} + e^{xy}\, \hat{ \mathbf k}$ and $\vecs{N}$ is an outward normal vector S, where S is the surface of sphere $x^2 + y^2 + z^2 = 1$.

Compute \[\int \int_S F \cdot N \, dS,\] where $F(x,y,z) = xyz\, \hat{ \mathbf i}+ xyz\, \hat{ \mathbf j} + xyz\, \hat{ \mathbf k}$ and $\vecs{N}$ is an outward normal vector S, where S is the surface of the five faces of the unit cube $0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1$ missing $z = 0$.

[Hide Solution]

\[\iint_S F \cdot N \, dS = \dfrac{3}{4}\]

For the following exercises, express the surface integral as an iterated double integral by using a projection on S on the yz-plane.

\[\iint_S xy^2 z^3 \, dS;\] S is the first-octant portion of plane $2x + 3y + 4z = 12$.

\[\iint_S (x^2 - 2y + z \, dS;\] S is the portion of the graph of $4x + y = 8$ bounded by the coordinate planes and plane $z = 6$.

[Hide Solution]

\[\int_0^8 \int_0^6 \left( 4 - 3y + \dfrac{1}{16} y^2 + z \right) \left(\dfrac{1}{4} \sqrt{17} \right) \, dz dy\]

Exercise $\PageIndex{10}$

For the following exercises, express the surface integral as an iterated double integral by using a projection on S on the xz-plane

\[\iint_S xy^2z^3 \, dS;\] S is the first-octant portion of plane $2x + 3y + 4z = 12$.

\[\iint_S (x^2 - 2y + z) \, dS;\] is the portion of the graph of $4x + y = 8$ bounded by the coordinate planes and plane $z = 6$.

[Hide Solution]

\[\int_0^2 \int_0^6 [x^2 - 2 (8 - 4x) + z] \sqrt{17} \, dz dx\]

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{11}$

Evaluate surface integral \[\iint_S yz \, dS,\] where S is the first-octant part of plane $x + y + z = \lambda$, where $\lambda$ is a positive constant.

Evaluate surface integral \[\iint_S (x^2 z + y^2 z) \, dS,\] where S is hemisphere $x^2 + y^2 + z^2 = a^2, \, z \geq 0.$

[Hide Solution]

\[\iint_S (x^2 z + y^2 z) \, dS = \dfrac{\pi a^5}{2}\]

Evaluate surface integral \[\iint_S zdA,\] where S is surface $z = \sqrt{x^2 + y^2}, \, 0 \leq z \leq 2$.

Evaluate surface integral \[\iint_S x^2 yz \, dS,\] where S is the part of plane $z = 1 + 2x + 3y$ that lies above rectangle $0 \leq x \leq 3$ and $0 \leq y \leq 2$.

[Hide Solution]

\[\iint_S x^2 yz \, dS = 171 \sqrt{14}\]

Evaluate surface integral \[\iint_S yz \, dS,\] where S is plane $x + y + z = 1$ that lies in the first octant.

Evaluate surface integral \[\iint_S yz \, dS,\] where S is the part of plane $z = y + 3$ that lies inside cylinder $x^2 + y^2 = 1$.

[Hide Solution]

\[\iint_S yz \, dS = \dfrac{\sqrt{2}\pi}{4}\]

Exercise $\PageIndex{12}$

For the following exercises, use geometric reasoning to evaluate the given surface integrals.

\[\iint_S \sqrt{x^2 + y^2 + z^2} \, dS,\] where S is surface $x^2 + y^2 + z^2 = 4, \, z \geq 0$

\[\iint_S (xi + yj) \cdot dS,\] where S is surface $x^2 + y^2 = 4, \, 1 \leq z \leq 3$, oriented with unit normal vectors pointing outward

[Hide Solution]

\[\iint_S (xi + yj) \cdot dS = 16 \pi\]

\[\iint_S (zk) \cdot dS,\] where S is disc $x^2 + y^2 \leq 9$ on plane $z = 4$ oriented with unit normal vectors pointing upward

Exercise $\PageIndex{13}$

A lamina has the shape of a portion of sphere $x^2 + y^2 + z^2 = a^2$ that lies within cone $z = \sqrt{x^2 + y^2}$. Let S be the spherical shell centered at the origin with radius a, and let C be the right circular cone with a vertex at the origin and an axis of symmetry that coincides with the z-axis. Determine the mass of the lamina if $\delta(x,y,z) = x^2 y^2 z$.

$A diagram in three dimensions. A cone opens upward with point at the origin and an asic of symmetry that coincides with the z-axis. The upper half of a hemisphere with center at the origin opens downward and is cut off by the xy-plane.$

[Hide Solution]

$m = \dfrac{\pi a^7}{192}$

A lamina has the shape of a portion of sphere $x^2 + y^2 + z^2 = a^2$ that lies within cone $z = \sqrt{x^2 + y^2}$. Let S be the spherical shell centered at the origin with radius a, and let C be the right circular cone with a vertex at the origin and an axis of symmetry that coincides with the z-axis. Suppose the vertex angle of the cone is $\phi_0$, with $0 \leq \phi_0 < \dfrac{\pi}{2}$. Determine the mass of that portion of the shape enclosed in the intersection of S and C. Assume $\delta(x,y,z) = x^2y^2z.$

A diagram in three dimensions. A cone opens upward with point at the origin and an asic of symmetry that coincides with the z-axis. The upper half of a hemisphere with center at the origin opens downward and is cut off by the xy-plane.

A paper cup has the shape of an inverted right circular cone of height 6 in. and radius of top 3 in. If the cup is full of water weighing $62.5 \, lb/ft^3$, find the total force exerted by the water on the inside surface of the cup.

[Hide Solution]

$F \approx 4.57 \, lb$

Exercise $\PageIndex{14}$

For the following exercises, the heat flow vector field for conducting objects $\vecs{F} = - k\nabla T$, where $T(x,y,z)$ is the temperature in the object and $k > 0$ is a constant that depends on the material. Find the outward flux of $\vecs{F}$ across the following surfaces S for the given temperature distributions and assume $k = 1$.

$T(x,y,z) = 100 e^{-x-y}$; S consists of the faces of cube $|x| \leq 1, \, |y| \leq 1, \, |z| \leq 1$.

$T(x,y,z) = - \ln (x^2 + y^2 + z^2)$; S is sphere $x^2 + y^2 + z^2 = a^2$.

[Hide Solution]

$8\pi a$

Exercise $\PageIndex{15}$

For the following exercises, consider the radial fields $F = \dfrac{\langle x,y,z \rangle}{(x^2+y^2+z^2)^{\dfrac{p}{2}}} = \dfrac{r}{|r|^p}$, where p is a real number. Let S consist of spheres A and B centered at the origin with radii $0 < a < b$. The total outward flux across S consists of the outward flux across the outer sphere B less the flux into S across inner sphere A.

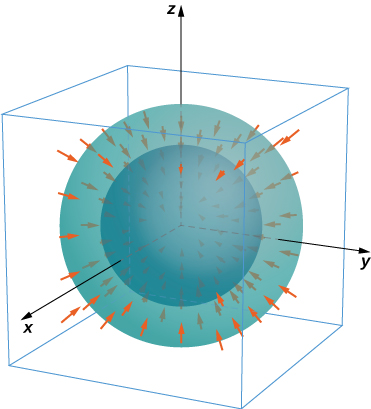
$A diagram in three dimensions of two spheres, one contained completely inside the other. Their centers are both at the origin. Arrows point in toward the origin from outside both spheres.$

Find the total flux across S with $p = 0$.

Show that for $p = 3$ the flux across S is independent of a and b.

Answer: The net flux is zero.

Exercise \(\PageIndex{1}\): True or false.

Exercise \(\PageIndex{3}\): Surface Area

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)