1.6: Polynomials and Rational Functions
- Last updated
- Aug 2, 2021
- Save as PDF
- Page ID
- 80878
( \newcommand{\kernel}{\mathrm{null}\,}\)
Polynomial Functions
Terminology of Polynomial Functions
A polynomial is function that can be written as f(x)=a0+a1x+a2x2+...+anxn
Each of the ai constants are called coefficients and can be positive, negative, or zero, and be whole numbers, decimals, or fractions.
A term of the polynomial is any one piece of the sum, that is any aixi. Each individual term is a transformed power function.
The degree of the polynomial is the highest power of the variable that occurs in the polynomial.
The leading term is the term containing the highest power of the variable: the term with the highest degree.
The leading coefficient is the coefficient of the leading term.
Because of the definition of the “leading” term we often rearrange polynomials so that the powers are descending.
f(x)=anxn+.....+a2x2+a1x+a0
Example 1.6.1
Identify the degree, leading term, and leading coefficient of the polynomial f(x)=3+2x2−4x3
Solution
For the function f(x), the degree is 3, the highest power on x. The leading term is the term containing that power, −4x3. The leading coefficient is the coefficient of that term, -4.
Short run Behavior: Intercepts
As with any function, the vertical intercept can be found by evaluating the function at an input of zero. Since this is evaluation, it is relatively easy to do it for a polynomial of any degree. To find horizontal intercepts, we need to solve for when the output will be zero. For general polynomials, this can be a challenging prospect. Consequently, we will limit ourselves to three cases:
- The polynomial can be factored using known methods: greatest common factor and trinomial factoring.
- The polynomial is given in factored form.
- Technology is used to determine the intercepts.
Example 1.6.2
Find the horizontal intercepts of f(x)=x6−3x4+2x2.
Solution
We can attempt to factor this polynomial to find solutions for f(x)=0. x6−3x4+2x2=0
x2(x4−3x2+2)=0 Factoring out the greatest common factorx2(x2−1)(x2−2)=0 Factoring the inside as a quadratic in x2
Then break apart to find solutions:
x2=0x=0 or (x2−1)=0x2=1x=±1 or (x2−2)=0x2=2x=±√2
This gives us 5 horizontal intercepts.
Example 1.6.3
Find the horizontal intercepts of h(t)=t3+4t2+t−6
Solution
Since this polynomial is not in factored form, has no common factors, and does not appear to be factorable using techniques we know, we can turn to technology to find the intercepts.
Graphing this function, it appears there are horizontal intercepts at t = -3, -2, and 1.
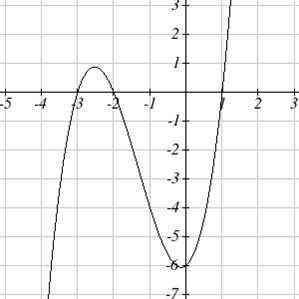
We could check these are correct by plugging in these values for t and verifying that h(−3)=h(−2)=h(1)=0.
Solving Polynomial Inequalities
One application of our ability to find intercepts and sketch a graph of polynomials is the ability to solve polynomial inequalities. It is a very common question to ask when a function will be positive and negative, and one we will use later in this course.
Example 1.6.4
Solve (x+3)(x+1)2(x−4)>0
Solution
As with all inequalities, we start by solving the equality (x+3)(x+1)2(x−4)=0, which has solutions at x = -3, -1, and 4. We know the function can only change from positive to negative at these values, so these divide the inputs into 4 intervals.
We could choose a test value in each interval and evaluate the function f(x)=(x+3)(x+1)2(x−4) at each test value to determine if the function is positive or negative in that interval
|
Interval |
Test x in interval |
f( test value) |
>0 or <0? |
|
x<−3 |
-4 |
72 |
> 0 |
|
−3<x<−1 |
-2 |
-6 |
< 0 |
|
−1<x<4 |
0 |
-12 |
< 0 |
|
x>4 |
5 |
288 |
> 0 |
On a number line this would look like:
From our test values, we can determine this function is positive when x<−3 or x>4, or in interval notation, (−∞,−3)∪(4,∞)
Rational Functions
Rational functions are the ratios, or fractions, of polynomials. They can arise from both simple and complex situations.
Example 1.6.5
You plan to drive 100 miles. Find a formula for the time the trip will take as a function of the speed you drive.
Solution
You may recall that multiplying speed by time will give you distance. If we let t represent the drive time in hours, and v represent the velocity (speed or rate) at which we drive, then vt= distance. Since our distance is fixed at 100 miles, vt=100. Solving this relationship for the time gives us the function we desired: t(v)=100v
Notice that this is a transformation of the reciprocal toolkit function,f(x)=1x. Several natural phenomena, such as gravitational force and volume of sound, behave in a manner inversely proportional to the square of another quantity. For example, the volume, V, of a sound heard at a distance d from the source would be related by V=kd2 for some constant value k. These functions are transformations of the reciprocal squared toolkit function f(x)=1x2.
We have seen the graphs of the basic reciprocal function and the squared reciprocal function from our review of toolkit functions. These graphs have several important features.
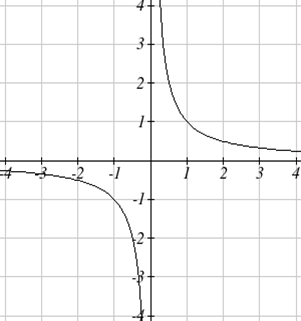
Let’s begin by looking at the reciprocal function, f(x)=1x. As you well know, dividing by zero is not allowed and therefore zero is not in the domain, and so the function is undefined at an input of zero.
Short run behavior:
As the input values approach zero from the left side (taking on very small, negative values), the function values become very large in the negative direction (in other words, they approach negative infinity).
We write: as x→0−,f(x)→−∞.
As we approach zero from the right side (small, positive input values), the function values become very large in the positive direction (approaching infinity).
We write: as x→0+,f(x)→∞.
This behavior creates a vertical asymptote. An asymptote is a line that the graph approaches. In this case the graph is approaching the vertical line x=0 as the input becomes close to zero.
Long run behavior:
As the values of x approach infinity, the function values approach 0.
As the values of x approach negative infinity, the function values approach 0.
Symbolically: as x→±∞,f(x)→0
Based on this long run behavior and the graph we can see that the function approaches 0 but never actually reaches 0, it just “levels off” as the inputs become large. This behavior creates a horizontal asymptote. In this case the graph is approaching the horizontal line f(x)=0 as the input becomes very large in the negative and positive directions.
Vertical and Horizontal Asymptotes
A vertical asymptote of a graph is a vertical line x=a where the graph tends towards positive or negative infinity as the inputs approach a. As x→a,f(x)→±∞.
A horizontal asymptote of a graph is a horizontal line y=b where the graph approaches the line as the inputs get large. As x→±∞,f(x)→b.
Example 1.6.6
Sketch a graph of the reciprocal function shifted two units to the left and up three units. Identify the horizontal and vertical asymptotes of the graph, if any.
Solution
Transforming the graph left 2 and up 3 would result in the function f(x)=1x+2+3, or equivalently, by giving the terms a common denominator, f(x)=3x+7x+2
Shifting the toolkit function would give us this graph.
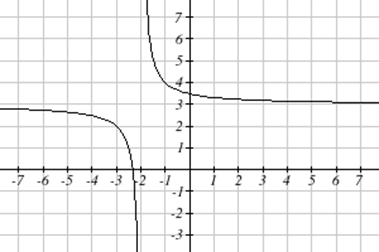
Notice that this equation is undefined at x=−2, and the graph also is showing a vertical asymptote at x=−2.
As x→−2−, f(x)→−∞, and as x→−2+, f(x)→∞
As the inputs grow large, the graph appears to be leveling off at output values of 3, indicating a horizontal asymptote at y=3.
As x→±∞, f(x)→3.
Notice that horizontal and vertical asymptotes get shifted left 2 and up 3 along with the function.
A general rational function is the ratio of any two polynomials.
Rational Function
A rational function is a function that can be written as the ratio of two polynomials, P(x) and Q(x).
f(x)=P(x)Q(x)=a0+a1x+a2x2+...+apxpb0+b1x+b2x2+...+bqxq
Rational functions can arise from real situations.
Example 1.6.7
A large mixing tank currently contains 100 gallons of water, into which 5 pounds of sugar have been mixed. A tap will open pouring 10 gallons per minute of water into the tank at the same time sugar is poured into the tank at a rate of 1 pound per minute. Find the concentration (pounds per gallon) of sugar in the tank after t minutes.
Solution
Notice that the amount of water in the tank is changing linearly, as is the amount of sugar in the tank. We can write an equation independently for each:
water=100+10tsugar=5+1t
The concentration, C, will be the ratio of pounds of sugar to gallons of water
C(t)=5+t100+10t
Vertical Asymptotes of Rational Functions
The vertical asymptotes of a rational function will occur where the denominator of the function is equal to zero and the numerator is not zero.
Horizontal Asymptote of Rational Functions
The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.
Degree of denominator > degree of numerator: Horizontal asymptote at y=0
Degree of denominator < degree of numerator: No horizontal asymptote
Degree of denominator = degree of numerator: Horizontal asymptote at ratio of leading coefficients.
Example 1.6.8
In the sugar concentration problem from earlier, we created the equation C(t)=5+t100+10t.
Find the horizontal asymptote and interpret it in context of the scenario.
Solution
Both the numerator and denominator are linear (degree 1), so since the degrees are equal, there will be a horizontal asymptote at the ratio of the leading coefficients. In the numerator, the leading term is t, with coefficient 1. In the denominator, the leading term is 10t, with coefficient 10. The horizontal asymptote will be at the ratio of these values: As t→∞, C(t)→110. This function will have a horizontal asymptote at y=110.
This tells us that as the input gets large, the output values will approach 1/10. In context, this means that as more time goes by, the concentration of sugar in the tank will approach one tenth of a pound of sugar per gallon of water or 1/10 pounds per gallon.
Example 1.6.9
Find the horizontal and vertical asymptotes of the function f(x)=(x−2)(x+3)(x−1)(x+2)(x−5)
Solution
First, note this function has no inputs that make both the numerator and denominator zero, so there are no potential holes. The function will have vertical asymptotes when the denominator is zero, causing the function to be undefined. The denominator will be zero at x = 1, -2, and 5, indicating vertical asymptotes at these values.
The numerator has degree 2, while the denominator has degree 3. Since the degree of the denominator is greater than the degree of the numerator, the denominator will grow faster than the numerator, causing the outputs to tend towards zero as the inputs get large, and so as x→±∞,f(x)→0. This function will have a horizontal asymptote at y=0.
As with all functions, a rational function will have a vertical intercept when the input is zero, if the function is defined at zero. It is possible for a rational function to not have a vertical intercept if the function is undefined at zero.
Likewise, a rational function will have horizontal intercepts at the inputs that cause the output to be zero (unless that input corresponds to a hole). It is possible there are no horizontal intercepts. Since a fraction is only equal to zero when the numerator is zero, horizontal intercepts will occur when the numerator of the rational function is equal to zero.
Example 1.6.10
Find the intercepts of f(x)=(x−2)(x+3)(x−1)(x+2)(x−5)
Solution
We can find the vertical intercept by evaluating the function at zero f(0)=(0−2)(0+3)(0−1)(0+2)(0−5)=−610=−35
The horizontal intercepts will occur when the function is equal to zero:
0=(x−2)(x+3)(x−1)(x+2)(x−5)
This is zero when the numerator is zero.
0=(x−2)(x+3)x=2,−3


