1.E: Review (Exercises)
- Last updated
- Save as PDF
- Page ID
- 80881
1.1 Exercises
Exercise \(\PageIndex{1}\)
The amount of garbage, \(G\), produced by a city with population \(p\) is given by \(G = f(p)\). \(G\) is measured in tons per week, and \(p\) is measured in thousands of people.
- The town of Tola has a population of 40,000 and produces 13 tons of garbage each week. Express this information in terms of the function \(f\).
- Explain the meaning of the statement \(f(5) = 2\).
Exercise \(\PageIndex{2}\)
The number of cubic yards of dirt, \(D\), needed to cover a garden with area \(a\) square feet is given by \(D = g(a)\).
- A garden with area 5000 \(ft^2\) requires 50 cubic yards of dirt. Express this information in terms of the function \(g\).
- Explain the meaning of the statement \(g(100) = 1\).
Exercise \(\PageIndex{3}\)
Select all of the following graphs which represent \(y\) as a function of \(x\).
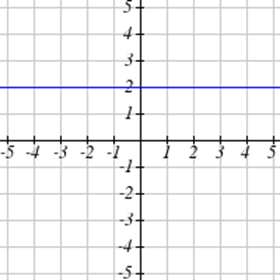
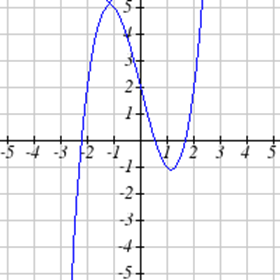
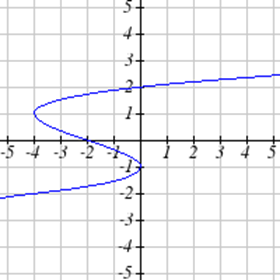
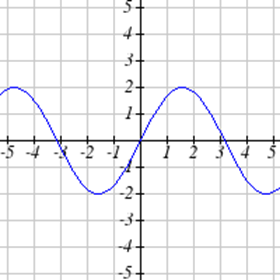
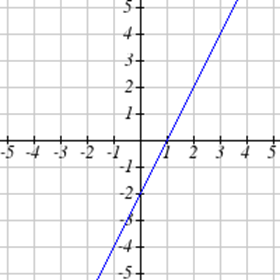
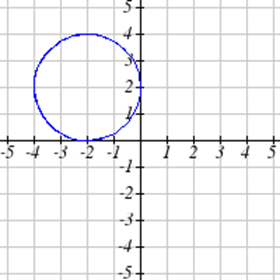
Exercise \(\PageIndex{4}\)
Select all of the following graphs which represent \(y\) as a function of \(x\).
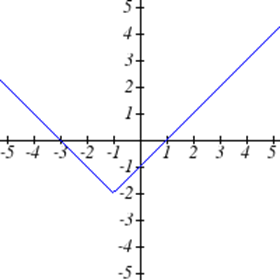
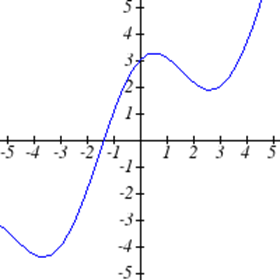
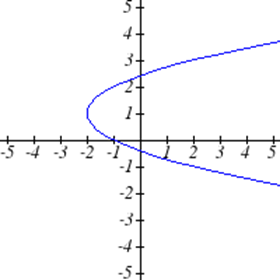
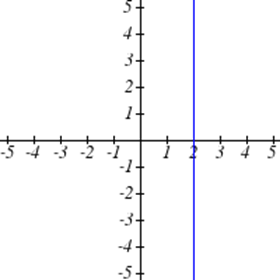
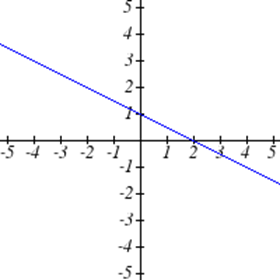
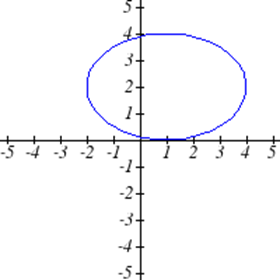
Exercise \(\PageIndex{5}\)
Select all of the following tables which represent \(y\) as a function of \(x\).
a.
|
x |
5 |
10 |
15 |
|
y |
3 |
8 |
14 |
b.
|
x |
5 |
10 |
15 |
|
y |
3 |
8 |
8 |
c.
|
x |
5 |
10 |
10 |
|
y |
3 |
8 |
14 |
Exercise \(\PageIndex{6}\)
Select all of the following tables which represent \(y\) as a function of \(x\).
a.
|
x |
2 |
6 |
13 |
|
y |
3 |
10 |
10 |
b.
|
x |
2 |
6 |
6 |
|
y |
3 |
10 |
14 |
c.
|
x |
2 |
6 |
13 |
|
y |
3 |
10 |
14 |
Exercise \(\PageIndex{7}\)
Given the function \(g(x)\) graphed here,
- Evaluate \(g(2)\)
- Solve \(g(x) = 2\)
Exercise \(\PageIndex{8}\)
Given the function \(f(x)\) graphed here.
- Evaluate \(f(4)\)
- Solve \(f(x) = 4\)
Exercise \(\PageIndex{9}\)
Based on the table below,
- Evaluate \(f(3)\)
- Solve \(f(x) = 1\)
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
\(f(x)\) |
74 |
28 |
1 |
53 |
56 |
3 |
36 |
45 |
14 |
47 |
Exercise \(\PageIndex{10}\)
Based on the table below,
- Evaluate \(f(8)\)
- Solve \(f(x) = 7\)
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
\(f(x)\) |
62 |
8 |
7 |
38 |
86 |
73 |
70 |
39 |
75 |
34 |
Exercises \(\PageIndex{11}-\PageIndex{18}\)
For each of the following functions, evaluate: \(f(-2)\), \(f(-1)\), \(f(0)\), \(f(1)\), and \(f(2)\)
| 11. \(f(x) = 4-2x\) | 12. \(f(x) = 8 - 3x\) |
| 13. \(f(x) = 8x^2 - 7x + 3\) | 14. \(f(x) = 6x^2 -7x+4\) |
| 15. \(f(x) = 3 + \sqrt{x+3}\) | 16. \(f(x) = 4 - \sqrt[3]{x-2}\) |
| 17. \(f(x) = \frac{x-3}{x+1}\) | 18. \(f(x) = \frac{x-2}{x+2}\) |
Exercise \(\PageIndex{19}\)
Let \(f(t) = 3t+5\)
- Evaluate \(f(0)\)
- Solve \(f(t) = 0\)
Exercise \(\PageIndex{20}\)
Let \(g(p) = 6 - 2p\)
- Evaluate \(g(0)\)
- Solve \(g(p) = 0\)
Exercise \(\PageIndex{21}\)
Using the graph shown,
- Evaluate \(f(c)\)
- Solve \(f(x) = p\)
- What are the coordinates of points \(L\) and \(K\)?
Exercise \(\PageIndex{22}\)
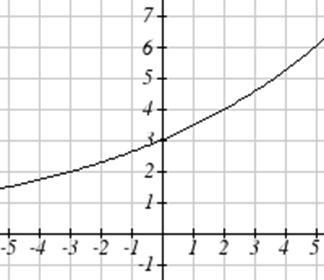
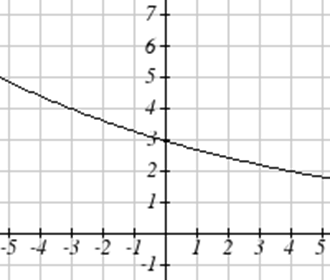
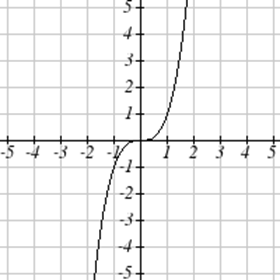
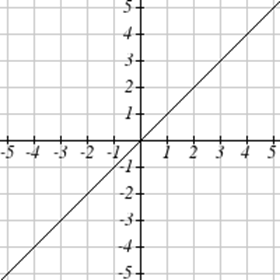
Match each graph with its equation.
| a. \(y=x\) | b. \(y = x^3\) | \(y = \sqrt[3]{x}\) | d. \(y = \frac{1}{x}\) |
| e. \(y = x^2\) | f. \(y = \sqrt{x}\) | g. \(y = |x|\) | h. \(y = \frac{1}{x^2}\) |
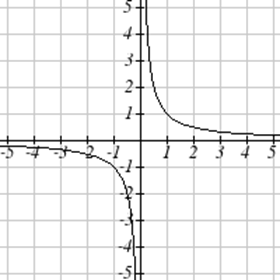
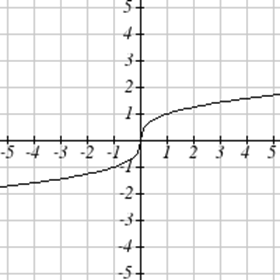
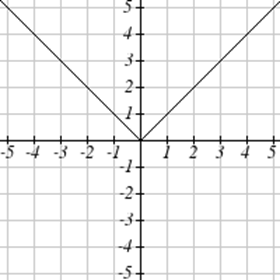
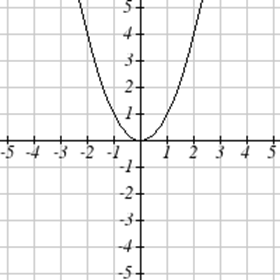
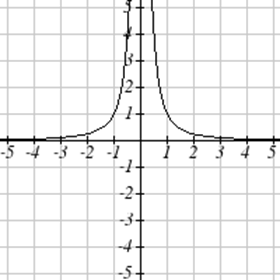
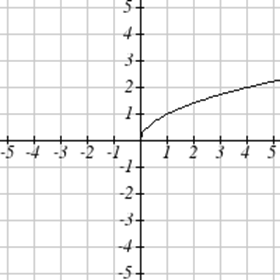
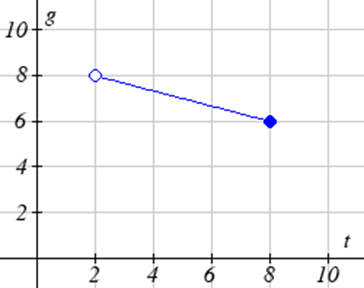
For Exercises \(\PageIndex{23}-\PageIndex{24}\), write the domain and range of each graph as an inequality.
Exercise \(\PageIndex{23}\)
Exercise \(\PageIndex{24}\)
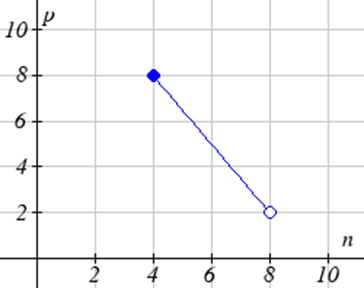
Exercise \(\PageIndex{25}-\PageIndex{30}\)
Find the domain of each function.
| 25. \(f(x) = 3\sqrt{x-2}\) | 26. \(f(x) = 5\sqrt{x+3}\) |
| 27. \(f(x) = \frac{9}{x-6}\) | 28. \(f(x) = \frac{6}{x-8}\) |
| 29. \(f(x) = \frac{3x+1}{4x+2}\) | 30. \(f(x) = \frac{5x+3}{4x-1}\) |
1.2 Exercises
Exercise \(\PageIndex{1}-\PageIndex{4}\)
| 1. \(f(x) = 4x+8, g(x) = 7-x^2\) | 2. \(f(x) = 5x+7, g(x) = 4-2x^2\) |
| 3. \(f(x) = \sqrt{x+4}, g(x) = 12-x^3\) | 4. \(f(x) = \frac{1}{x+2}, g(x) = 4x+3\) |
Exercise \(\PageIndex{5}-\PageIndex{12}\)
|
x |
\(f(x)\) |
\(g(x)\) |
|
0 |
7 |
9 |
|
1 |
6 |
5 |
|
2 |
5 |
6 |
|
3 |
8 |
2 |
|
4 |
4 |
1 |
|
5 |
0 |
8 |
|
6 |
2 |
7 |
|
7 |
1 |
3 |
|
8 |
9 |
4 |
|
9 |
3 |
0 |
Use the table of values to evaluate each expression.
| 5. \(f(g(8))\) |
| 6. \(f(g(5))\) |
| 7. \(g(f(5))\) |
| 8. \(g(f(3))\) |
| 9. \(f(f(4))\) |
| 10. \(f(f(1))\) |
| 11. \(g(g(2))\) |
| 12. \(g(g(6))\) |
Exercise \(\PageIndex{13}-\PageIndex{20}\)
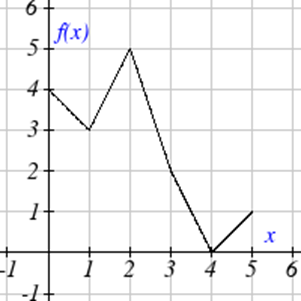
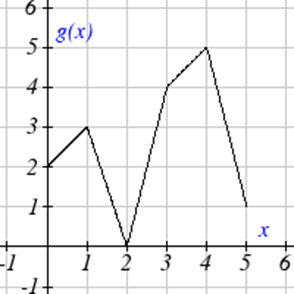
Use the graphs to evaluate the expressions below.
| 13. \(f(g(3))\) |
| 14. \(f(g(1))\) |
| 15. \(g(f(1))\) |
| 16. \(g(f(0))\) |
| 17. \(f(f(5))\) |
| 18. \(f(f(4))\) |
| 19. \(g(g(2))\) |
| 20. \(g(g(0))\) |
Exercise \(\PageIndex{21}-\PageIndex{26}\)
For each pair of functions, find \(f(g(x))\) and \(g(f(x))\). Simplify your answers.
| 21. \(f(x) = \frac{1}{x-6}, g(x) = \frac{7}{x}+6\) | 22. \(f(x) = \frac{1}{x-4}, g(x) = \frac{2}{x} + 4\) |
| 23. \(f(x) = x^2+1, g(x) = \sqrt{x+2}\) | 24. \(f(x) = \sqrt{x} + 2, g(x) = x^2 + 3\) |
| 25. \(f(x) = |x|, g(x) = 5x+1\) | 26. \(f(x) = \sqrt[3]{x}, g(x) = \frac{x+1}{x^3}\) |
Exercise \(\PageIndex{27}\)
If \(f(x) = x^4+6\), \(g(x) = x - 6\), and \(h(x) = \sqrt{x}\), find \(f(g(h(x)))\)
Exercise \(\PageIndex{28}\)
If \(f(x) = x^2+1\), \(g(x) = \frac{1}{x}\), and \(h(x) = x+3\), find \(f(g(h(x)))\)
Exercise \(\PageIndex{29}\)
The function \(D(p)\) gives the number of items that will be demanded when the price is \(p\). The production cost, \(C(x)\) is the cost of producing \(x\) items. To determine the cost of production when the price is $6, you would do which of the following:
- Evaluate \(D(C(6))\)
- Solve \(C(D(6))\)
- Evaluate \(D(C(x)) = 6\)
- Solve \(C(D(p)) = 6\)
Exercise \(\PageIndex{30}\)
The function \(A(d)\) gives the pain level on a scale of 0-10 experienced by a patient with \(d\) milligrams of a pain reduction drug in their system. The milligrams of drug in the patient’s system after \(t\) minutes is modeled by \(m(t)\). To determine when the patient will be at a pain level of 4, you would need to:
- Evaluate \(A(m(4))\)
- Solve \(m(A(4))\)
- Evaluate \(A(m(t)) = 4\)
- Solve \(m(A(d)) = 4\)
Exercise \(\PageIndex{31}-\PageIndex{36}\)
Find functions \(f(x)\) and \(g(x)\) so the given function can be expressed as \(h(x) = f(g(x))\).
| 31. \(h(x) = (x+2)^2\) | 32. \(h(x) = (x-5)^3\) |
| 33. \(h(x) = \frac{3}{x-5}\) | 34. \(h(x) = \frac{4}{(x+2)^2}\) |
| 35. \(h(x) = 3+\sqrt{x-2}\) | 36. \(h(x) = 4+\sqrt[3]{x}\) |
Exercise \(\PageIndex{37}-\PageIndex{44}\)
Sketch a graph of each function as a transformation of a toolkit function.
| 37. \(f(t) = (t+1)^2 - 3\) | 38. \(h(x) = |x-1|+4\) |
| 39. \(k(x) =(x-2)^3 -1\) | 40. \(m(t) = 3+\sqrt{t+2}\) |
| 41. \(f(x) = 4(x+1)^2 - 5\) | 42. \(g(x) = 5(x+3)^2 - 2\) |
| 43. \(h(x) = -2|x-4|+3\) | 44. \(k(x) = -3\sqrt{x} - 1\) |
Exercise \(\PageIndex{45}-\PageIndex{50}\)
Write an equation for each function graphed below.
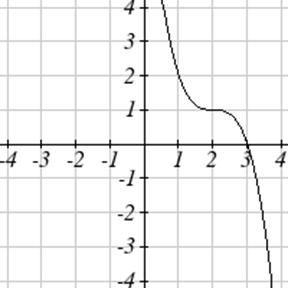
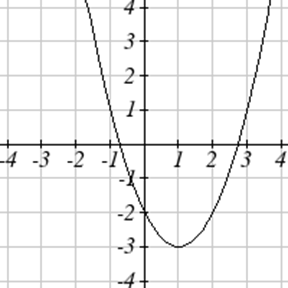
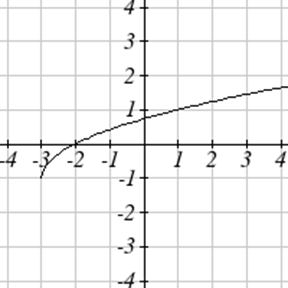
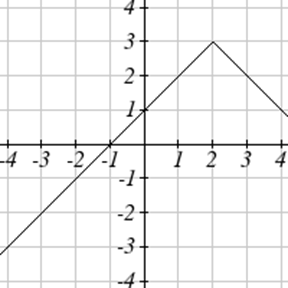
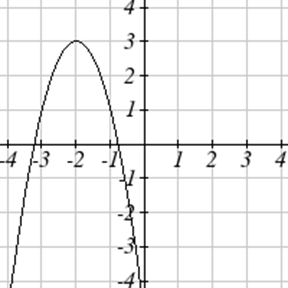
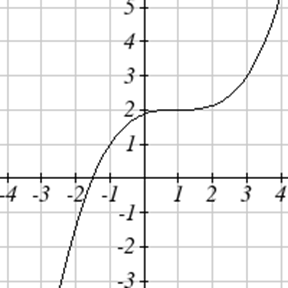
Exercise \(\PageIndex{51}-\PageIndex{52}\)
For each function graphed, estimate the intervals on which the function is increasing and decreasing.
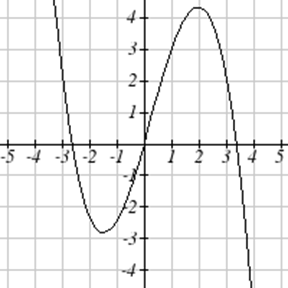
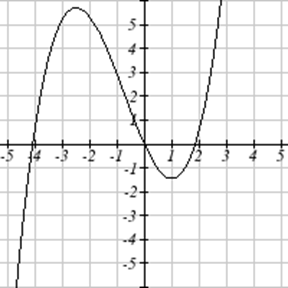 52.
52.1.3 Exercises
Exercise \(\PageIndex{1}\)
A town's population has been growing linearly. In 2003, the population was 45,000, and the population has been growing by 1700 people each year. Write an equation, \(P(t)\), for the population \(t\) years after 2003.
Exercise \(\PageIndex{2}\)
A town's population has been growing linearly. In 2005, the population was 69,000, and the population has been growing by 2500 people each year. Write an equation, \(P(t)\), for the population \(t\) years after 2005.
Exercise \(\PageIndex{3}\)
Timmy goes to the fair with $40. Each ride costs $2. How much money will he have left after riding \(n\) rides?
Exercise \(\PageIndex{4}\)
At noon, a barista notices she has $20 in her tip jar. If she makes an average of $0.50 from each customer, how much will she have in her tip jar if she serves \(n\) more customers during her shift?
Exercise \(\PageIndex{5}\)
A phone company charges for service according to the formula: \(C(n) = 24+0.1n\), where \(n\) is the number of minutes talked, and \(C(n)\) is the monthly charge, in dollars.
Find and interpret the rate of change and initial value.
Exercise \(\PageIndex{6}\)
A phone company charges for service according to the formula: \(C(n) = 26+0.04n\), where \(n\) is the number of minutes talked, and \(C(n)\) is the monthly charge, in dollars.
Find and interpret the rate of change and initial value.
Exercise \(\PageIndex{7}-\PageIndex{14}\)
Given each set of information, find a linear equation satisfying the conditions, if possible.
| 7. \(f(-5) = -4\), and \(f(5)=2\) | 8. \(f(-1)=4\), and \(f(5)=1\) |
| 9. Passes through (2,4) and (4,10) | 10. Passes through (1, 5) and (4, 11) |
| 11. Passes through (-1,4) and (5, 2) | 12. Passes through (-2, 8) and (4, 6) |
| 13. \(x\) intercept at (-2, 0) and \(y\) intercept at (0, -3) | 14. \(x\) intercept at (-5, 0) and \(y\) intercept at (0, 4) |
Exercise \(\PageIndex{15}-\PageIndex{16}\)
Find an equation for the function graphed.
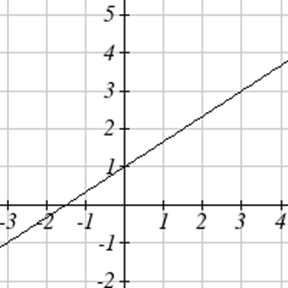
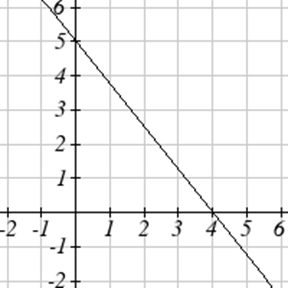
Exercise \(\PageIndex{17}\)
A clothing business finds there is a linear relationship between the number of shirts, \(n\), it can sell and the price, \(p\), it can charge per shirt. In particular, historical data shows that 1000 shirts can be sold at a price of $30, while 3000 shirts can be sold at a price of $22. Find a linear equation in the form \(p=mn+b\) that gives the price \(p\) they can charge for \(n\) shirts.
Exercise \(\PageIndex{18}\)
A farmer finds there is a linear relationship between the number of bean stalks, \(n\), she plants and the yield, \(y\), each plant produces. When she plants 30 stalks, each plant yields 30 oz of beans. When she plants 34 stalks, each plant produces 28 oz of beans. Find a linear relationships in the form \(y=mn+b\) that gives the yield when \(n\) stalks are planted.
Exercise \(\PageIndex{19}-\PageIndex{24}\)
Match each linear equation with its graph
| 19. \(f(x) = -x-1\) |
| 20. \(f(x) = -2x-1\) |
| 21. \(f(x) = -\frac{1}{2}x-1\) |
| 22. \(f(x) = 2\) |
| 23. \(f(x) = 2+x\) |
| 24. \(f(x) = 3x+2\) |
Exercise \(\PageIndex{25}-\PageIndex{28}\)
Sketch the graph of each equation
| 25. \(f(x) = -2x-1\) | 26. \(g(x) = -3x+2\) |
| 27. \(h(x)=\frac{1}{3}x+2\) | 28. \(k(x) = \frac{2}{3}x-3\) |
Exercise \(\PageIndex{29}\)
Find the point at which the line \(f(x) = -2x-1\) intersects the line \(g(x)=-x\)
Exercise \(\PageIndex{30}\)
Find the point at which the line \(f(x)=2x+5\) intersects the line \(g(x)=-3x-5\)
Exercise \(\PageIndex{31}\)
A car rental company offers two plans for renting a car.
Plan A: 30 dollars per day and 18 cents per mile
Plan B: 50 dollars per day with free unlimited mileage
How many miles would you need to drive for plan B to save you money?
Exercise \(\PageIndex{32}\)
A cell phone company offers two data options for its prepaid phones
Pay per use: $0.002 per Kilobyte (KB) used
Data Package: $5 for 5 Megabytes (5120 Kilobytes) + $0.002 per addition KB
Assuming you will use less than 5 Megabytes, under what circumstances will the data package save you money?
Exercise \(\PageIndex{33}\)
The Federal Helium Reserve held about 16 billion cubic feet of helium in 2010, and is being depleted by about 2.1 billion cubic feet each year.
- Give a linear equation for the remaining federal helium reserves, \(R\), in terms of \(t\), the number of years since 2010.
- In 2015, what will the helium reserves be?
- If the rate of depletion doesn’t change, when will the Federal Helium Reserve be depleted?
Exercise \(\PageIndex{34}\)
Suppose the world's current oil reserves are 1820 billion barrels. If, on average, the total reserves is decreasing by 25 billion barrels of oil each year:
- Give a linear equation for the remaining oil reserves, \(R\), in terms of \(t\), the number of years since now.
- Seven years from now, what will the oil reserves be?
- If the rate of depletion isn’t change, when will the world’s oil reserves be depleted?
1.4 Exercises
Exercise \(\PageIndex{1}-\PageIndex{8}\)
Simplify each expression
| 1. \(x^3x^5\) | 2. \(x^4x^2\) |
| 3. \(\left(x^3\right)^4\) | 4. \(\left(x^7\right)^2\) |
| 5. \(\left(2x^2\right)^3x^4\) | 6. \(\left(5x^4\right)^2x^5\) |
| 7. \(\frac{\left(3x^2\right)^2}{6x^3}\) | 8. \(\frac{5x\left(4x\right)^2}{2x^2}\) |
Exercise \(\PageIndex{9}-\PageIndex{14}\)
Simplify, and rewrite without negative exponents
| 9. \(4x^{-3}\) | 10. \(2x^{-5}\) |
| 11. \(x^{-4}x^2\) | 12. \(x^{-2}x\) |
| 13. \(\frac{5x^{-3}}{2x^{-6}}\) | 14. \(\frac{2x^{-4}}{6x^{-2}}\) |
Exercise \(\PageIndex{15}-\PageIndex{20}\)
Rewrite using negative or fractional exponents
| 15. \(\frac{4}{x^{-5}}\) | 16. \(\frac{4}{x^{-3}}\) |
| 17. \(3\sqrt{x}\) | 18. \(\sqrt[4]{x}\) |
| 19. \(\frac{4}{\sqrt[3]{x}}\) | 20. \(\frac{1}{5\sqrt{x}}\) |
Exercise \(\PageIndex{21}-\PageIndex{24}\)
Rewrite as a radical
| 21. \(4x^{-\frac{1}{2}}\) | 22. \(5x^{-\frac{1}{3}}\) |
| 23. \(2x^{\frac{1}{3}}\) | 24. \(5x^{\frac{3}{2}}\) |
1.5 Exercises
Exercise \(\PageIndex{1}-\PageIndex{6}\)
Write an equation for the quadratic function graphed.
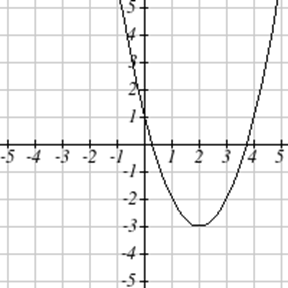
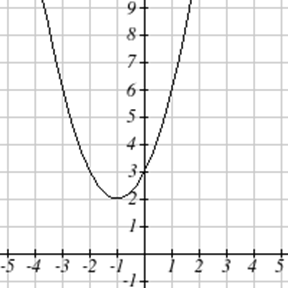
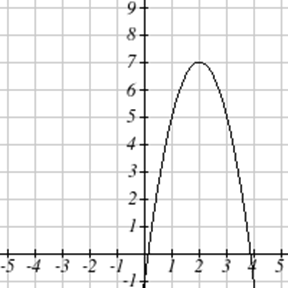
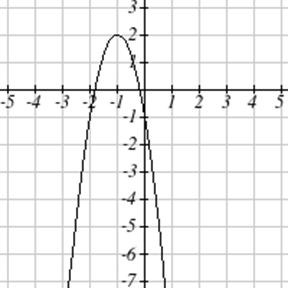
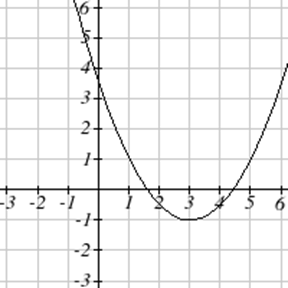
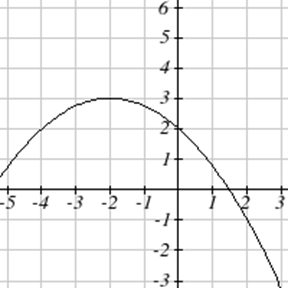
Exercise \(\PageIndex{7}-\PageIndex{12}\)
| 7. \(y(x) = 2x^2+10x+12\) | 8. \(z(p)=3x^2+6x-9\) |
| 9. \(f(x)=2x^2-10x+4\) | 10. \(g(x) = -2x^2-14x+12\) |
| 11. \(h(t)=-4t^2+6t-1\) | 12. \(k(t) = 2x^2+4x-15\) |
Exercise \(\PageIndex{13}\)
The height of a ball thrown in the air is given by \(h(x) = -\frac{1}{12}x^2+6x+3\), where \(x\) is the horizontal distance in feet from the point at which the ball is thrown.
- How high is the ball when it was thrown?
- What is the maximum height of the ball?
- How far from the thrower does the ball strike the ground?
Exercise \(\PageIndex{14}\)
A javelin is thrown in the air. Its height is given by \(h(x)=-\frac{1}{20}x^2+8x+6\), where \(x\) is the horizontal distance in feet from the point at which the javelin is thrown.
- How high is the javelin when it was thrown?
- What is the maximum height of the javelin?
- How far from the thrower does the javelin strike the ground?
1.6 Exercises
Exercise \(\PageIndex{1}-\PageIndex{6}\)
Find the degree and leading coefficient of each polynomial
| 1. \(4x^7\) | 2. \(5x^6\) |
| 3. \(5-x^2\) | 4. \(6+3x-4x^3\) |
| 5. \(-2x^4-3x^2+x-1\) | 6. \(6x^5-2x^4+x^2+3\) |
Exercise \(\PageIndex{7}-\PageIndex{12}\)
Find the vertical and horizontal intercepts of each function.
| 7. \(f(t) = 2(t-1)(t+2)(t-3)\) | 8. \(f(x)=3(x+1)(x-4)(x+5)\) |
| 9. \(g(n) = -2(3n-1)(2n+1)\) | 10. \(k(u)=-3(4-n)(4n+3)\) |
| 11. \(C(t) = 2t^4-8t^3+6t^2\) | 12. \(C(t)=4t^4+12t^3-40t^2\) |
Exercise \(\PageIndex{13}-\PageIndex{14}\)
Use your calculator or other graphing technology to solve graphically for the zeros of the function.
| 13. \(f(x) = x^3 - 7x^2+4x+30\) | 14. \(g(x)=x^3-6x^2+x+28\) |
Exercise \(\PageIndex{15}-\PageIndex{18}\)
Solve each inequality.
| 15. \((x-3)(x-2)^2>0\) | 16. \((x-5)(x+1)^2>0\) |
| 17. \((x-1)(x+2)(x-3)<0\) | 18. \((x-4)(x+3)(x+6)<0\) |
Exercise \(\PageIndex{19}-\PageIndex{26}\)
For each function, find the horizontal intercepts, the vertical intercept, the vertical asymptotes, and the horizontal asymptote.
| 19. \(p(x) = \frac{2x-3}{x+4}\) | 20. \(q(x) = \frac{x-5}{3x-1}\) |
| 21. \(s(x) = \frac{4}{(x-2)^2}\) | 22. \(r(x) = \frac{5}{(x+1)^2}\) |
| 23. \(f(x) = \frac{3x^2-14x-5}{3x^2+8x-16}\) | 24. \(g(x) = \frac{2x^2+7x-15}{3x^2-14+15}\) |
| 25. \(h(x) = \frac{2x^2+x-1}{x-4}\) | 26. \(k(x) = \frac{2x^2-3x-20}{x-5}\) |
Exercise \(\PageIndex{27}\)
A scientist has a beaker containing 20 mL of a solution containing 20% acid. To dilute this, she adds pure water.
- Write an equation for the concentration in the beaker after adding \(n\) mL of water.
- Find the concentration if 10 mL of water has been added.
- How many mL of water must be added to obtain a 4% solution?
- What is the behavior as \(n \to \infty\), and what is the physical significance of this?
Exercise \(\PageIndex{28}\)
A scientist has a beaker containing 30 mL of a solution containing 3 grams of potassium hydroxide. To this, she mixes a solution containing 8 milligrams per mL of potassium hydroxide.
- Write an equation for the concentration in the tank after adding \(n\) mL of the second solution.
- Find the concentration if 10 mL of the second solution has been added.
- How many mL of water must be added to obtain a 50 mg/mL solution?
- What is the behavior as \(n \to \infty\), and what is the physical significance of this?
1.7 Exercises
Exercise \(\PageIndex{1}\)
A population numbers 11,000 organisms initially and grows by 8.5% each year. Write an exponential model for the population.
Exercise \(\PageIndex{2}\)
A population is currently 6,000 and has been increasing by 1.2% each day. Write an exponential model for the population.
Exercise \(\PageIndex{3}\)
A vehicle purchased for $32,500 depreciates at a constant rate of 5% each year. Determine the approximate value of the vehicle 12 years after purchase.
Exercise \(\PageIndex{4}\)
A business purchases $125,000 of office furniture which depreciates at a constant rate of 12% each year. Find the residual value of the furniture 6 years after purchase.
Exercise \(\PageIndex{5}\)
If $4,000 is invested in a bank account at an interest rate of 7 per cent per year, find the amount in the bank after 9 years if interest is compounded annually, quarterly, monthly, and continuously.
Exercise \(\PageIndex{6}\)
If $6,000 is invested in a bank account at an interest rate of 9 per cent per year, find the amount in the bank after 5 years if interest is compounded annually, quarterly, monthly, and continuously.
Exercise \(\PageIndex{7}-\PageIndex{12}\)
Match each function with one of the graphs below.
| 7. \(f(x) = 2(0.69)^x\) |
| 8. \(f(x) = 2(1.28)^x\) |
| 9. \(f(x) = 2(0.81)^x\) |
| 10 \(f(x) = 4(1.28)^x\) |
| 11. \(f(x) = 2(1.59)^x\) |
| 12. \(f(x) = 4(0.69)^x\) |
Exercise \(\PageIndex{13}-\PageIndex{16}\)
If all the graphs to the right have equations with form \(f(t) = ae^{kt}\),
|
13. Which graph has the largest value for \(k\)? |
|
14. Which graph has the smallest value for \(k\)? |
|
15. Which graph has the largest value for \(a\)? |
|
16. Which graph has the smallest value for \(a\)? |
1.8 Exercises
Exercise \(\PageIndex{1}-\PageIndex{4}\)
Rewrite each equation in exponential form
| 1. \(\log (v) = t\) | 2. \(\log (r) = s\) | 3. \(\ln (w) = n\) | 4. \(\ln (x) = y\) |
Exercise \(\PageIndex{5}-\PageIndex{8}\)
Rewrite each equation in logarithmic form.
| 5. \(10^a = b\) | 6. \(10^p = v\) | 7. \(e^k = h\) | 8. \(e^y = x\) |
Exercise \(\PageIndex{9}-\PageIndex{24}\)
Solve each equation for the variable.
| 9. \(5^{x} = 14\) | 10. \(3^x = 23\) | 11. \(7^x = \frac{1}{15}\) | 12. \(3^x = \frac{1}{4}\) |
| 13. \(e^{5x} = 17\) | 14. \(e^{3x} = 12\) | 15. \(3^{4x-5} = 38\) | 16. \(4^{2x-3} = 44\) |
| 17. \(1000(1.03)^t = 5000\) | 18. \(200(1.06)^t = 550\) |
| 19. \(3(1.04)^{3t} = 8\) | 20. \(2(1.08)^{4t} = 7\) |
| 21. \(50e^{-0.12t} = 10\) | 22. \(10e^{-0.03t} = 4\) |
| 23. \(10 - 8 \left(\frac{1}{2}\right)^x = 5\) | 24. \(100-100\left(\frac{1}{4}\right)^x = 70\) |
Exercise \(\PageIndex{25}\)
The population of Kenya was 39.8 million in 2009 and has been growing by about 2.6% each year. If this trend continues, when will the population exceed 45 million?
Exercise \(\PageIndex{26}\)
The population of Algeria was 34.9 million in 2009 and has been growing by about 1.5% each year. If this trend continues, when will the population exceed 45 million?
Exercise \(\PageIndex{27}\)
If $1000 is invested in an account earning 3% compounded monthly, how long will it take the account to grow in value to $1500?
Exercise \(\PageIndex{28}\)
If $1000 is invested in an account earning 2% compounded quarterly, how long will it take the account to grow in value to $1300?
Exercise \(\PageIndex{29}\)
Sketch a graph of: \(f(x) = \log (x)\), \(g(x) = \ln (x)\)
Exercise \(\PageIndex{30}-\PageIndex{33}\)
Find the domain of each function.
| 30. \(f(x) = \log (x-5)\) | 31. \(f(x) = \ln (3-x)\) |
| 32. \(f(x) = \ln (1-3x)\) | 33. \(f(x) = \log (2x+5)\) |

