For exercises 1 - 5, examine the graphs. Identify where the vertical asymptotes are located.
1)
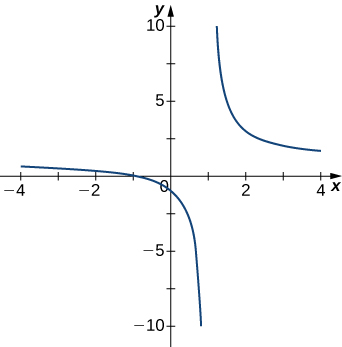
- Answer
- \(x=1\)
2)
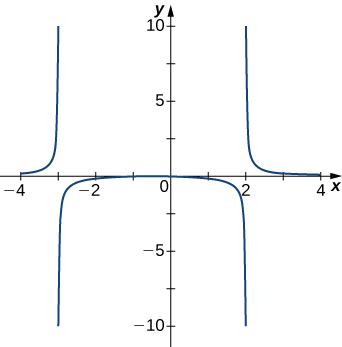
3)
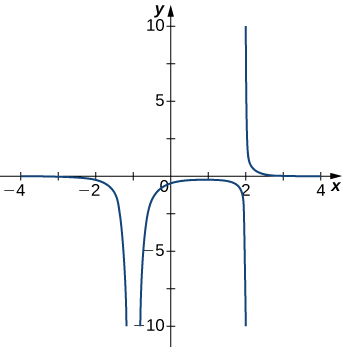
- Answer
- \(x=−1,\;x=2\)
4)
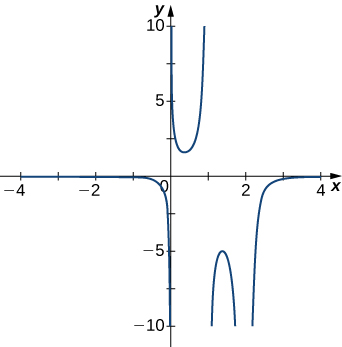
5)
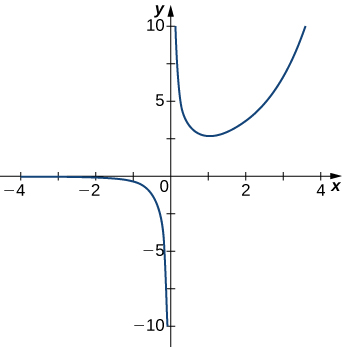
- Answer
- \(x=0\)
For the functions \(f(x)\) in exercises 6 - 10, determine whether there is an asymptote at \(x=a\). Justify your answer without graphing on a calculator.
6) \(f(x)=\dfrac{x+1}{x^2+5x+4},\quad a=−1\)
7) \(f(x)=\dfrac{x}{x−2},\quad a=2\)
- Answer
- Yes, there is a vertical asymptote at \(x = 2\).
8) \(f(x)=(x+2)^{3/2},\quad a=−2\)
9) \(f(x)=(x−1)^{−1/3},\quad a=1\)
- Answer
- Yes, there is vertical asymptote at \(x = 1\).
10) \(f(x)=1+x^{−2/5},\quad a=1\)
In exercises 11 - 20, evaluate the limit.
11) \(\displaystyle \lim_{x→∞}\frac{1}{3x+6}\)
- Answer
- \(\displaystyle \lim_{x→∞}\frac{1}{3x+6} = 0\)
12) \(\displaystyle \lim_{x→∞}\frac{2x−5}{4x}\)
13) \(\displaystyle \lim_{x→∞}\frac{x^2−2x+5}{x+2}\)
- Answer
- \(\displaystyle \lim_{x→∞}\frac{x^2−2x+5}{x+2} = ∞\)
14) \(\displaystyle \lim_{x→−∞}\frac{3x^3−2x}{x^2+2x+8}\)
15) \(\displaystyle \lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4}\)
- Answer
- \(\displaystyle \lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4} = −\frac{1}{7}\)
16) \(\displaystyle \lim_{x→∞}\frac{3x}{\sqrt{x^2+1}}\)
17) \(\displaystyle \lim_{x→−∞}\frac{\sqrt{4x^2−1}}{x+2}\)
- Answer
- \(\displaystyle \lim_{x→−∞}\frac{\sqrt{4x^2−1}}{x+2} = -2\)
18) \(\displaystyle \lim_{x→∞}\frac{4x}{\sqrt{x^2−1}}\)
19) \(\displaystyle \lim_{x→−∞}\frac{4x}{\sqrt{x^2−1}}\)
- Answer
- \(\displaystyle \lim_{x→−∞}\frac{4x}{\sqrt{x^2−1}} = -4\)
20) \(\displaystyle \lim_{x→∞}\frac{2\sqrt{x}}{x−\sqrt{x}+1}\)
For exercises 21 - 25, find the horizontal and vertical asymptotes.
21) \(f(x)=x−\dfrac{9}{x}\)
- Answer
- Horizontal: none,
Vertical: \(x=0\)
22) \(f(x)=\dfrac{1}{1−x^2}\)
23) \(f(x)=\dfrac{x^3}{4−x^2}\)
- Answer
- Horizontal: none,
Vertical: \(x=±2\)
24) \(f(x)=\dfrac{x^2+3}{x^2+1}\)
25) \(f(x)=\sin(x)\sin(2x)\)
- Answer
- Horizontal: none,
Vertical: none
26) \(f(x)=\cos x+\cos(3x)+\cos(5x)\)
27) \(f(x)=\dfrac{x\sin(x)}{x^2−1}\)
- Answer
- Horizontal: \(y=0,\)
Vertical: \(x=±1\)
28) \(f(x)=\dfrac{x}{\sin(x)}\)
29) \(f(x)=\dfrac{1}{x^3+x^2}\)
- Answer
- Horizontal: \(y=0,\)
Vertical: \(x=0\) and \(x=−1\)
30) \(f(x)=\dfrac{1}{x−1}−2x\)
31) \(f(x)=\dfrac{x^3+1}{x^3−1}\)
- Answer
- Horizontal: \(y=1,\)
Vertical: \(x=1\)
32) \(f(x)=\dfrac{\sin x+\cos x}{\sin x−\cos x}\)
33) \(f(x)=x−\sin x\)
- Answer
- Horizontal: none,
Vertical: none
34) \(f(x)=\dfrac{1}{x}−\sqrt{x}\)
For exercises 35 - 38, construct a function \(f(x)\) that has the given asymptotes.
35) \(x=1\) and \(y=2\)
- Answer
- Answers will vary, for example: \(y=\dfrac{2x}{x−1}\)
36) \(x=1\) and \(y=0\)
37) \(y=4, \;x=−1\)
- Answer
- Answers will vary, for example: \(y=\dfrac{4x}{x+1}\)
38) \(x=0\)
In exercises 39 - 43, graph the function on a graphing calculator on the window \(x=[−5,5]\) and estimate the horizontal asymptote or limit. Then, calculate the actual horizontal asymptote or limit.
39) [T] \(f(x)=\dfrac{1}{x+10}\)
- Answer
- \(\displaystyle \lim_{x→∞}\frac{1}{x+10}=0\) so \(f\) has a horizontal asymptote of \(y=0\).
40) [T] \(f(x)=\dfrac{x+1}{x^2+7x+6}\)
41) [T] \(\displaystyle \lim_{x→−∞}x^2+10x+25\)
- Answer
- \(\displaystyle \lim_{x→−∞}x^2+10x+25 = ∞\)
42) [T] \(\displaystyle \lim_{x→−∞}\frac{x+2}{x^2+7x+6}\)
43) [T] \(\displaystyle \lim_{x→∞}\frac{3x+2}{x+5}\)
- Answer
- \(\displaystyle \lim_{x→∞}\frac{3x+2}{x+5}=3\) so this function has a horizontal asymptote of \(y=3\).
Contributors and Attributions







