4.3E: Exercises for Section 4.3
- Last updated
- Save as PDF
- Page ID
- 80089
1) T/F: If \(c\) is a critical value of a function \(f\), then \(f\) has either a relative maximum or relative minimum at \(x=c\).
- Answer:
- False. \(f\) may have a plateau point when \(x = c\).
2) In precalculus, you learned a formula for the position of the maximum or minimum of a quadratic equation \(y=ax^2+bx+c\), which was \(m=−\frac{b}{2a}\). Prove this formula using calculus.
3) If you are finding an absolute minimum over an interval \([a,b],\) why do you need to check the endpoints? Draw a graph that supports your hypothesis.
- Answer:
- On a closed interval, the endpoints often lie above or below any local (relative) extrema. Answers may vary for the graph.
4) If you are examining a function over an interval \((a,b),\) for \(a\) and \(b\) finite, is it possible not to have an absolute maximum or absolute minimum?
5) When you are checking for critical points to locate the extrema of a function \(f\), explain why you also need to determine points where \(f'(x)\) is undefined. Draw a graph to support your explanation.
- Answer:
- Points on the graph of \(f\) where there is a corner, a cusp, or a jump discontinuity or removable discontinuity can easily be absolute (or local) extrema of the function. Answers may vary for the graph.
6) Can you have a finite absolute maximum for \(y=ax^2+bx+c\) over \((−∞,∞)\)? Explain why or why not using graphical arguments.
7) Can you have a finite absolute maximum for \(y=ax^3+bx^2+cx+d\) over \((−∞,∞)\) assuming \(a\) is non-zero? Explain why or why not using graphical arguments.
- Answer:
- No; answers will vary
8) Let \(m\) be the number of local minima and \(M\) be the number of local maxima. Can you create a function where \(M>m+2\)? Draw a graph to support your explanation.
9) Is it possible to have more than one absolute maximum? Use a graphical argument to prove your hypothesis.
- Answer:
- Since the absolute maximum is the function (output) value rather than the x value, the answer is no; answers will vary
10) Is it possible to have no absolute minimum or maximum for a function? If so, construct such a function. If not, explain why this is not possible.
11) [T] Graph the function \(y=e^{ax}.\) For which values of \(a\), on any infinite domain, will you have an absolute minimum and absolute maximum?
- Answer:
- Only when \(a=0\) would this function attain an absolute minimum and absolute maximum.
In exercises 12 - 15, determine where the local and absolute maxima and minima occur on the graph given. Assume domains are closed intervals unless otherwise specified.
12)
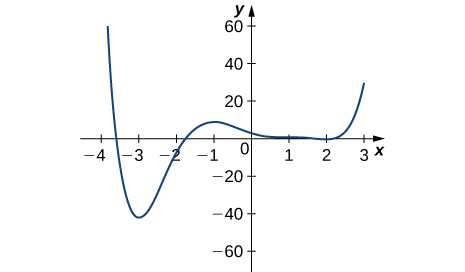
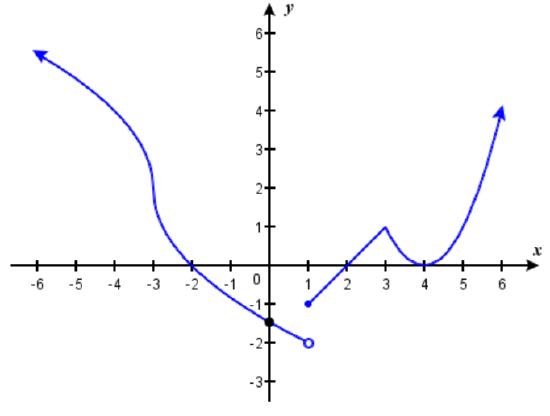
13)
- Answer:
- Absolute minimum of about \(-20\) at \(x = 3\);
Absolute maximum of about \(10\) at about \(x = −2.2\);
Local Minima at \(x= −2\) and \(x = 1\);
Local Maxima at \(x = −1\) and \(x = 2\)
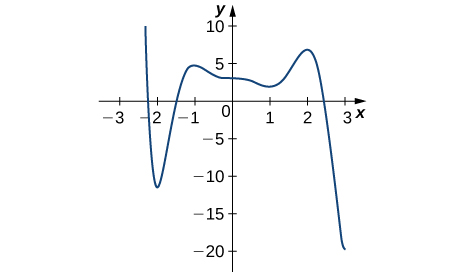
14)
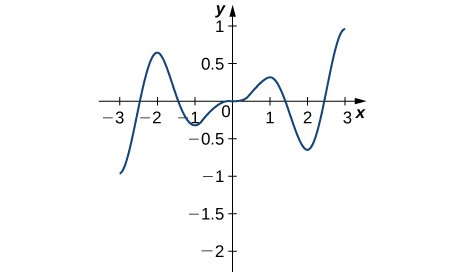
15)
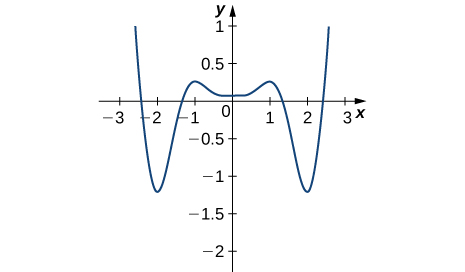
- Answer:
- Absolute minima of about \(-1.25\) at \(x = −2\) and \(x = 2\);
Absolute maxima of \(1\) at \(x = −2.5\) and \(x = 2.5\);
Local minimum at \(x = 0\);
Local maxima at \(x = −1\) and \(x = 1\)
For exercises 16 - 19, draw graphs of \(f(x)\), which is continuous, over the interval \([−4,4]\) with the following properties:
16) Absolute maximum at \(x=2\) and absolute minima at \(x=±3\)
17) Absolute minimum at \(x=1\) and absolute maximum at \(x=2\)
- Answer:
- Answers may vary.
18) Absolute maximum at \(x=4,\) absolute minimum at \(x=−1,\) local maximum at \(x=−2,\) and a critical point that is not a maximum or minimum at \(x=2\)
19) Absolute maxima at \(x=2\) and \(x=−3\), local minimum at \(x=1\), and absolute minimum at \(x=4\)
- Answer:
- Answers may vary.
In exercises 20 - 29, find the critical points in the domains of the given functions.
20) \(y=4x^3−3x\)
21) \(y=4\sqrt{x}−x^2\)
- Answer:
- \(x=1\)
22) \(y=\dfrac{1}{x−1}\)
23) \(y=\ln(x−2)\)
- Answer:
- None
24) \(y=\tan(x)\)
25) \(y=\sqrt{4−x^2}\)
- Answer:
- \(x=0\)
26) \(y=x^{3/2}−3x^{5/2}\)
27) \(y=\dfrac{x^2−1}{x^2+2x−3}\)
- Answer:
- None
28) \(y=\sin^2(x)\)
29) \(y=x+\dfrac{1}{x}\)
- Answer:
- \(x=−1\) and \(x = 1\)
In exercises 30 - 31, identify each of the marked points as being an absolute maximum and minimum, a relative maximum or minimum, or none of the above. Also indicate at which points the function is defined, but the function's derivative does not exist.
30)
31)
- Answer:
- A: none of the above
B: absolute maximum
C: relative minimum
D: none of the above
E: none of the above
F: relative minimum
G: none of the above
The function is undefined at points: A and D
The function's derivative does not exist at points: C and E, since the function has a sudden change in direction at each point.
In exercises 32 - 33, state the values of \(x\) at which the derivative of the following functions do not exist and give an explanation.
32)
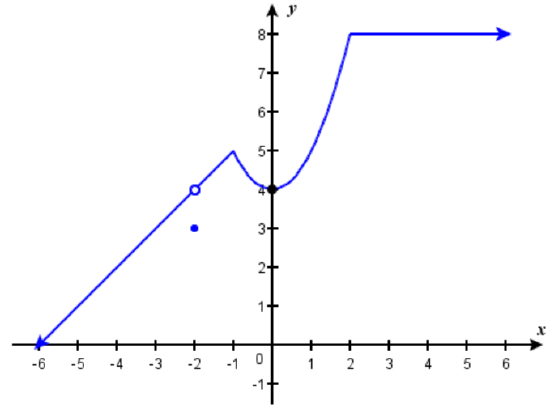
- Answer:
- This function's derivative does not exist at:
\(x = -3\), since \(f\) would have a vertical tangent line there,
\(x = 1\), since \(f\) has a jump discontinuity there,
\(x = 3\), since \(f\) has a corner (or abrupt change in direction) there.
Note that all of these are also critical numbers, since the function is defined at each of these values of \(x\).
\(x = 4\) is also a critical number, but here the derivative equals \(0\).
In exercises 34 - 44, find the local and/or absolute maxima for the functions over the specified domain.
34) \(f(x)=x^2+3\) over \([−1,4]\)
35) \(f(x)=x^2+\dfrac{2}{x}\) over \([1,4]\)
- Answer:
- The absolute maximum of \(f\) on \([1,4]\) is \(\frac{33}{2}\) when \(x=4\).
The absolute minimum of \(f\) on \([1,4]\) is \(3\) when \(x=1\).
36) \(y=(x−x^2)^2\) over \([−1,1]\)
37) \(y=\dfrac{1}{x−x^2}\) over \([0,1]\)
- Answer:
- The absolute minimum of this function on \([0,1]\) is \(y=4\) when \(x=\frac{1}{2}\).
There is no absolute maximum.
Note that this function is not continuous at \(x = 0\) or \(x = 1\), so it does not satisfy the Extreme Value Theorem.
38) \(y=\sqrt{9−x}\) over \([1,9]\)
39) \(y=x+\sin(x)\) over \([0,2π]\)
- Answer:
- The absolute maximum of this function on \([0,2π]\) is \(y=2π\) when \(x=2π\).
The absolute minimum of this function on \([0,2π]\) is \(y=0\) when \(x=0\).
40) \(y=\dfrac{x}{1+x}\) over \([0,100]\)
41) \(y=|x+1|+|x−1|\) over \([−3,2]\)
- Answer:
- The absolute maximum of this function on \([−3,2]\) is \(y=6\) when \(x=-3\).
The absolute minimum of this function on \([−3,2]\) is \(y=2\) when \(−1≤x≤1\).
If you haven't done so already, try graphing this function in Desmos or another graphing app.
42) \(y=\sqrt{x}−\sqrt{x^3}\) over \([0,4]\)
43) \(y=\sin x+\cos x\) over \([0,2π]\)
- Answer:
- The absolute maximum of this function on \([0,2π]\) is \(y=\sqrt{2}\) when \(x=\frac{π}{4}\).
The absolute minimum of this function on \([0,2π]\) is \(y=-\sqrt{2}\) when \(x=\frac{5π}{4}\).
44) \(y=4\sin θ−3\cos θ\) over \([0,2π]\)
In exercises 45 - 50, find the local and absolute minima and maxima for the functions over \((−∞,∞).\)
45) \(y=x^2+4x+5\)
- Answer:
- The absolute minimum is located at the point \((-2, 1)\). That is, the abs. min. is \(y=1\) when \(x=−2\).
46) \(y=x^3−12x\)
47) \(y=3x^4+8x^3−18x^2\)
- Answer:
- The absolute minimum of this function is located at the point \((-3, -135)\). That is, the abs. min. is \(y=−135\) when \(x=−3\).
A local maximum of this function is located at the point \((0, 0)\). That is, it has a local max. of \(y=0\) when \(x=0\).
A local minimum of this function is located at the point \((1, -7)\). That is, it has a local min. of \(y=-7\) when \(x=1\).
48) \(y=x^3(1−x)^6\)
49) \(y=\dfrac{x^2+x+6}{x−1}\)
- Answer:
- A local maximum of this function is \(y=3−4\sqrt{2}\) when \(x=1−2\sqrt{2}\).
A local minimum of this function is \(y=3+4\sqrt{2}\) when \(x=1+2\sqrt{2}\).
50) \(y=\dfrac{x^2−1}{x−1}\)
In exercises 51 - 55, use a calculator to graph the function and to estimate the absolute and local maxima and minima. Then, solve for them explicitly.
51) [T] \(y=3x\sqrt{1−x^2}\)
- Answer:
- Absolute maximum: \(y=\frac{3}{2};\) when \(x=\frac{\sqrt{2}}{2}\)
Absolute minimum: \(y=−\frac{3}{2}\) when \(x=−\frac{\sqrt{2}}{2}\)
52) [T] \(y=x+\sin(x)\)
53) [T] \(y=12x^5+45x^4+20x^3−90x^2−120x+3\)
- Answer:
- Local maximum: \(y=59\) when \(x=−2\)
Local minimum: \(y=−130\) when \(x=1\)
54) [T] \(y=\dfrac{x^3+6x^2−x−30}{x−2}\)
55) [T] \(y=\dfrac{\sqrt{4−x^2}}{\sqrt{4+x^2}}\)
- Answer:
- Absolute maximum: \(y=1\) when \(x=0\)
Absolute minimum: \(y=0\) when \(x=−2\) or \(x=2\)
56) A company that produces cell phones has a cost function of \(C=x^2−1200x+36,400,\) where \(C\) is cost in dollars and \(x\) is number of cell phones produced (in thousands). How many units of cell phone (in thousands) minimizes this cost function?
57) A ball is thrown into the air and its position is given by \(h(t)=−4.9t^2+60t+5m.\) Find the height at which the ball stops ascending. How long after it is thrown does this happen?
- Answer:
- \(h=\frac{9245}{49}\) m, \(t=\frac{300}{49}\) s
For exercises 58-59, consider the production of gold during the California gold rush (1848–1888). The production of gold can be modeled by \(G(t)=\dfrac{(25t)}{(t^2+16)}\), where \(t\) is the number of years since the rush began \((0≤t≤40)\) and \(G\) is ounces of gold produced (in millions). A summary of the data is shown in the following figure.
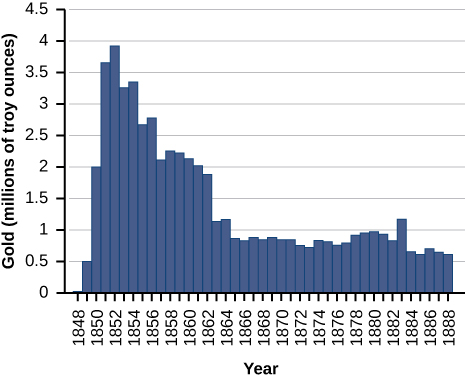
58) Find when the maximum (local and global) gold production occurred, and the amount of gold produced during that maximum.
59) Find when the minimum (local and global) gold production occurred. What was the amount of gold produced during this minimum?
- Answer:
- The global minimum was in 1848, when no gold was produced.
In exercises 60 - 61, find the critical points, maxima, and minima for the given piecewise functions.
60) \(y= \begin{cases} x^2−4x, & \text{if }0≤x≤1\\x^2−4, & \text{if }1<x≤2 \end{cases}\)
61) \(y=\begin{cases}x^2+1, & \text{if }x≤1 \\ x^2−4x+5, & \text{if }x>1\end{cases}\)
- Answer:
- Absolute minima: \(x=0, x=2, y=1\); local maximum at \(x=1, y=2\)
In exercises 62 - 63, find the critical points of the following generic functions. Are they maxima, minima, or neither? State the necessary conditions.
62) \(y=ax^2+bx+c,\) given that \(a>0\)
63) \(y=(x−1)^a\), given that \(a>1\)
- Answer:
- No maxima/minima if \(a\) is odd, minimum at \(x=1\) if \(a\) is even
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/
Exercises 1, 30, and 31.- Paul Seeburger (Monroe Community College) added exercises 32, 33, and added or expanded answers for exercises 1, 3, 5, 11, 13, 15, 31, 33, and 35-55 odd. Also added last part of instructions for exercises 30 - 31 (originally from Apex Calculus).