1) If \(c\) is a critical point of \(f(x)\), when is there no local maximum or minimum at \(c\)? Explain.
2) For the function \(y=x^3\), is \(x=0\) both an inflection point and a local maximum/minimum?
- Answer
- It is not a local maximum/minimum because \(f'\) does not change sign
3) For the function \(y=x^3\), is \(x=0\) an inflection point?
4) Is it possible for a point \(c\) to be both an inflection point and a local extremum of a twice differentiable function?
- Answer
- No
5) Why do you need continuity for the first derivative test? Come up with an example.
6) Explain whether a concave-down function has to cross \(y=0\) for some value of \(x\).
- Answer
- False; for example, \(y=\sqrt{x}\).
7) Explain whether a polynomial of degree \(2\) can have an inflection point.
In exercises 8 - 12, analyze the graphs of \(f'\), then list all intervals where \(f\) is increasing or decreasing.
8)
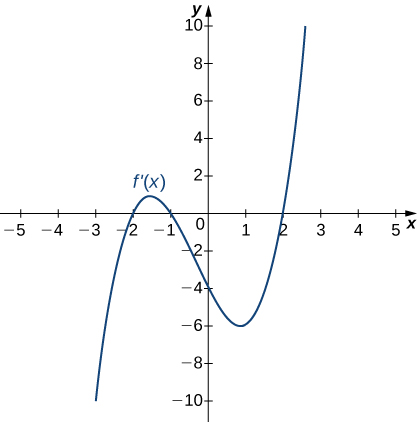
- Answer
- Increasing for \(−2<x<−1\) and \(x>2\);
Decreasing for \(x<−2\) and \(−1<x<2\)
9)
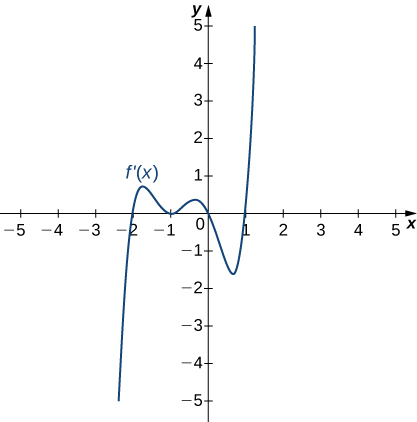
10)
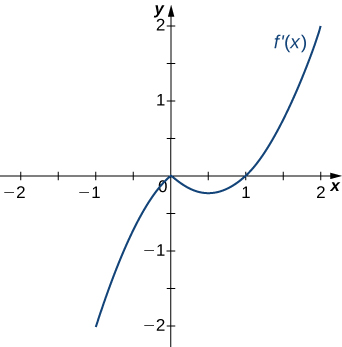
- Answer
- Decreasing for \(x<1\),
Increasing for \(x>1\)
11)
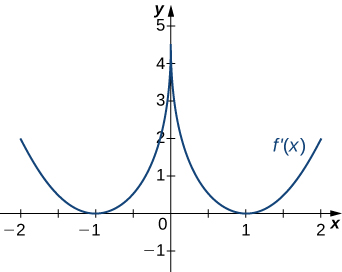
12)
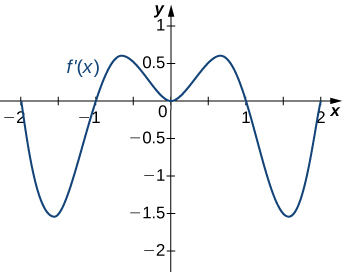
- Answer
- Decreasing for \(−2<x<−1\) and \(1<x<2\);
Increasing for \(−1<x<1\) and \(x<−2\) and \(x>2\)
In exercises 13 - 17, analyze the graphs of \(f'\), then list all intervals where
a. \(f\) is increasing and decreasing and
b. the minima and maxima are located.
13)
14)
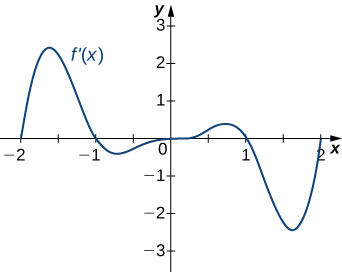
- Answer
- a. Increasing over \(−2<x<−1,\;0<x<1,x>2\), Decreasing over \(x<−2, \;−1<x<0, \;1<x<2;\)
b. Maxima at \(x=−1\) and \(x=1\), Minima at \(x=−2\) and \(x=0\) and \(x=2\)
15)
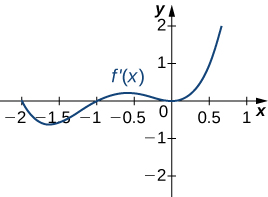
16)
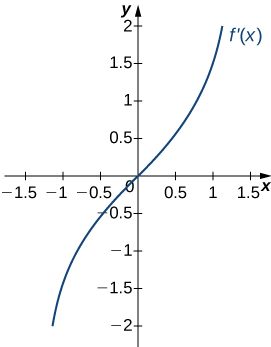
- Answer
- a. Increasing over \(x>0\), Decreasing over \(x<0;\)
b. Minimum at \(x=0\)
17)
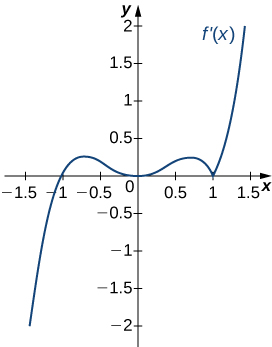
In exercises 18 - 22, analyze the graphs of \(f'\), then list all inflection points and intervals \(f\) that are concave up and concave down.
18)
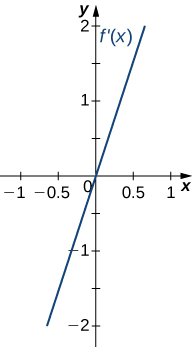
- Answer
- Concave up for all \(x\),
No inflection points
19)
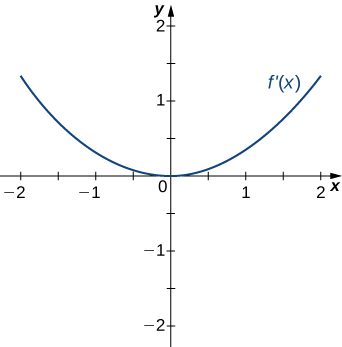
20)
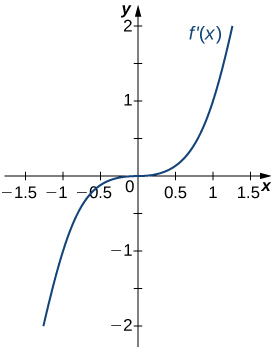
- Answer
- Concave up for all \(x\),
No inflection points
21)
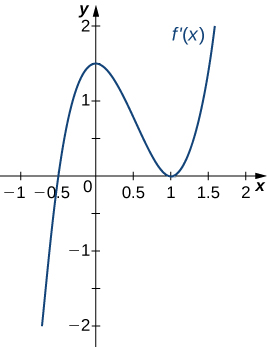
22)
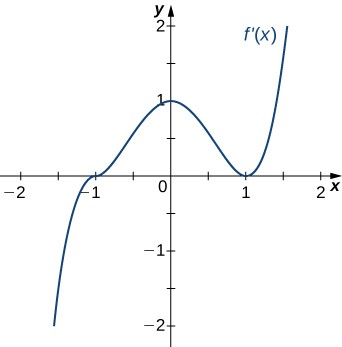
- Answer
- Concave up for \(x<0\) and \(x>1\),
Concave down for \(0<x<1\),
Inflection points at \(x=0\) and \(x=1\)
For exercises 23 - 27, draw a graph that satisfies the given specifications for the domain \(x=[−3,3]\). The function does not have to be continuous or differentiable.
23) \(f(x)>0,\;f'(x)>0\) over \(x>1,\;−3<x<0,\;f'(x)=0\) over \(0<x<1\)
24) \(f'(x)>0\) over \(x>2,\;−3<x<−1,\;f'(x)<0\) over \(−1<x<2,\;f''(x)<0\) for all \(x\)
- Answer
- Answers will vary
25) \(f''(x)<0\) over \(−1<x<1,\;f''(x)>0,\;−3<x<−1,\;1<x<3,\) local maximum at \(x=0,\) local minima at \(x=±2\)
26) There is a local maximum at \(x=2,\) local minimum at \(x=1,\) and the graph is neither concave up nor concave down.
- Answer
- Answers will vary
27) There are local maxima at \(x=±1,\) the function is concave up for all \(x\), and the function remains positive for all \(x.\)
For the following exercises, determine
a. intervals where \(f\) is increasing or decreasing and
b. local minima and maxima of \(f\).
28) \(f(x)=\sin x+\sin^3x\) over \(−π<x<π\)
- Answer
-
a. Increasing over \(−\frac{π}{2}<x<\frac{π}{2},\) decreasing over \(x<−\frac{π}{2},\; x>\frac{π}{2}\)
b. Local maximum at \(x=\frac{π}{2}\); local minimum at \(x=−\frac{π}{2}\)
29) \(f(x)=x^2+\cos x\)
For exercise 30, determine
a. intervals where \(f\) is concave up or concave down, and
b. the inflection points of \(f\).
30) \(f(x)=x^3−4x^2+x+2\)
- Answer
-
a. Concave up for \(x>\frac{4}{3},\) concave down for \(x<\frac{4}{3}\)
b. Inflection point at \(x=\frac{4}{3}\)
For exercises 31 - 37, determine
a. intervals where \(f\) is increasing or decreasing,
b. local minima and maxima of \(f\),
c. intervals where \(f\) is concave up and concave down, and
d. the inflection points of \(f\).
31) \(f(x)=x^2−6x\)
32) \(f(x)=x^3−6x^2\)
- Answer
- a. Increasing over \(x<0\) and \(x>4,\) decreasing over \(0<x<4\)
b. Maximum at \(x=0\), minimum at \(x=4\)
c. Concave up for \(x>2\), concave down for \(x<2\)
d. Inflection point at \(x=2\)
33) \(f(x)=x^4−6x^3\)
34) \(f(x)=x^{11}−6x^{10}\)
- Answer
- a. Increasing over \(x<0\) and \(x>\frac{60}{11}\), decreasing over \(0<x<\frac{60}{11}\)
b. Maximum at \(x=0\), minimum at \(x=\frac{60}{11}\)
c. Concave down for \(x<\frac{54}{11}\), concave up for \(x>\frac{54}{11}\)
d. Inflection point at \(x=\frac{54}{11}\)
35) \(f(x)=x+x^2−x^3\)
36) \(f(x)=x^2+x+1\)
- Answer
- a. Increasing over \(x>−\frac{1}{2}\), decreasing over \(x<−\frac{1}{2}\)
b. Minimum at \(x=−\frac{1}{2}\)
c. Concave up for all \(x\)
d. No inflection points
37) \(f(x)=x^3+x^4\)
For exercises 38 - 47, determine
a. intervals where \(f\) is increasing or decreasing,
b. local minima and maxima of \(f\),
c. intervals where \(f\) is concave up and concave down, and
d. the inflection points of \(f\). Sketch the curve, then use a calculator to compare your answer. If you cannot determine the exact answer analytically, use a calculator.
38) [T] \(f(x)=\sin(πx)−\cos(πx)\) over \(x=[−1,1]\)
- Answer
- a. Increases over \(−\frac{1}{4}<x<\frac{3}{4},\) decreases over \(x>\frac{3}{4}\) and \(x<−\frac{1}{4}\)
b. Minimum at \(x=−\frac{1}{4}\), maximum at \(x=\frac{3}{4}\)
c. Concave up for \(−\frac{3}{4}<x<\frac{1}{4}\), concave down for \(x<−\frac{3}{4}\) and \(x>\frac{1}{4}\)
d. Inflection points at \(x=−\frac{3}{4},\;x=\frac{1}{4}\)
39) [T] \(f(x)=x+\sin(2x)\) over \(x=[−\frac{π}{2},\frac{π}{2}]\)
40) [T] \(f(x)=\sin x+\tan x\) over \((−\frac{π}{2},\frac{π}{2})\)
- Answer
- a. Increasing for all \(x\)
b. No local minimum or maximum
c. Concave up for \(x>0\), concave down for \(x<0\)
d. Inflection point at \(x=0\)
41) [T] \(f(x)=(x−2)^2(x−4)^2\)
42) [T] \(f(x)=\dfrac{1}{1−x},\quad x≠1\)
- Answer
- a. Increasing for all \(x\) where defined
b. No local minima or maxima
c. Concave up for \(x<1\); concave down for \(x>1\)
d. No inflection points in domain
43) [T] \(f(x)=\dfrac{\sin x}{x}\) over \(x=[-2π,0)∪(0,2π]\)
44) \(f(x)=\sin(x)e^x\) over \(x=[−π,π]\)
- Answer
- a. Increasing over \(−\frac{π}{4}<x<\frac{3π}{4}\), decreasing over \(x>\frac{3π}{4},\;x<−\frac{π}{4}\)
b. Minimum at \(x=−\frac{π}{4}\), maximum at \(x=\frac{3π}{4}\)
c. Concave up for \(−\frac{π}{2}<x<\frac{π}{2}\), concave down for \(x<−\frac{π}{2},\;x>\frac{π}{2}\)
d. Inflection points at \(x=±\frac{π}{2}\)
45) \(f(x)=\ln x\sqrt{x},\quad x>0\)
46) \(f(x)=\frac{1}{4}\sqrt{x}+\frac{1}{x},\quad x>0\)
- Answer
- a. Increasing over \(x>4,\) decreasing over \(0<x<4\)
b. Minimum at \(x=4\)
c. Concave up for \(0<x<8\sqrt[3]{2}\), concave down for \(x>8\sqrt[3]{2}\)
d. Inflection point at \(x=8\sqrt[3]{2}\)
47) \(f(x)=\dfrac{e^x}{x},\quad x≠0\)
In exercises 48 - 52, interpret the sentences in terms of \(f\), \(f'\), and \(f''\).
48) The population is growing more slowly. Here \(f\) is the population.
- Answer
- \(f>0,\;f'>0,\;f''<0\)
49) A bike accelerates faster, but a car goes faster. Here \(f=\) Bike’s position minus Car’s position.
50) The airplane lands smoothly. Here \(f\) is the plane’s altitude.
- Answer
- \(f>0,\;f'<0,\;f''>0\)
51) Stock prices are at their peak. Here \(f\)is the stock price.
52) The economy is picking up speed. Here \(f\) is a measure of the economy, such as GDP.
- Answer
- \(f>0,\;f'>0,\;f''>0\)
For exercises 53 - 57, consider a third-degree polynomial \(f(x)\), which has the properties \(f'(1)=0\) and \(f'(3)=0\).
Determine whether the following statements are true or false. Justify your answer.
53) \(f(x)=0\) for some \(1≤x≤3\).
54) \(f''(x)=0\) for some \(1≤x≤3\).
- Answer
- True, by the Mean Value Theorem
55) There is no absolute maximum at \(x=3\).
56) If \(f(x)\) has three roots, then it has \(1\) inflection point.
- Answer
- True, examine derivative
57) If \(f(x)\) has one inflection point, then it has three real roots.

















