1.4: Composition of Functions

Create a Function by Composition of Functions

Performing algebraic operations on functions combines them into a new function, but we can also create functions by composing functions. When we wanted to compute a heating cost from a day of the year, we created a new function that takes a day as input and yields a cost as output. The process of combining functions so that the output of one function becomes the input of another is known as a composition of functions. The resulting function is known as a composite function. We represent this combination by the following notation:

\[f{\circ}g(x)=f(g(x))\]

We read the left-hand side as“\(f\) composed with \(g\) at \(x\),” and the right-hand side as“\(f\) of \(g\) of \(x\).”The two sides of the equation have the same mathematical meaning and are equal. The open circle symbol \(\circ\) is called the composition operator. We use this operator mainly when we wish to emphasize the relationship between the functions themselves without referring to any particular input value. Composition is a binary operation that takes two functions and forms a new function, much as addition or multiplication takes two numbers and gives a new number. However, it is important not to confuse function composition with multiplication because, as we learned above, in most cases \(f(g(x)){\neq}f(x)g(x)\).

It is also important to understand the order of operations in evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first, and then working to the outside. In the equation above, the function \(g\) takes the input \(x\) first and yields an output \(g(x)\). Then the function \(f\) takes \(g(x)\) as an input and yields an output \(f(g(x))\).

Figure \(\PageIndex{2}\): Explanation of the composite function.

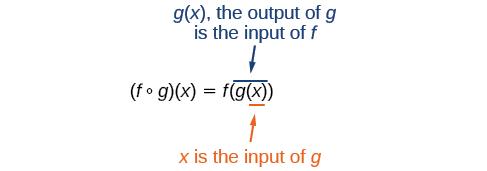
In general, \(f{\circ}g\) and \(g{\circ}f\) are different functions. In other words, in many cases \(f(g(x)){\neq}g(f(x))\) for all \(x\). We will also see that sometimes two functions can be composed only in one specific order.

For example, if \(f(x)=x^2\) and \(g(x)=x+2\), then

\[\begin{align*} f(g(x))&= f(x+2) \\[4pt]&=(x+2)^2 \\[4pt] &=x^2+4x+4 \end{align*}\]

but

\[\begin{align*} g(f(x))&= g(x^2) \\[4pt]&=x^2+2 \end{align*}\]

These expressions are not equal for all values of x, so the two functions are not equal. It is irrelevant that the expressions happen to be equal for the single input value \(x=−\frac{1}{2}\).

Note that the range of the inside function (the first function to be evaluated) needs to be within the domain of the outside function. Less formally, the composition has to make sense in terms of inputs and outputs.

Composition of Functions

When the output of one function is used as the input of another, we call the entire operation a composition of functions. For any input \(x\) and functions \(f\) and \(g\), this action defines a composite function, which we write as \(f{\circ}g\) such that

\[(f{\circ}g)(x)=f(g(x))\]

The domain of the composite function \(f{\circ}g\) is all \(x\) such that \(x\) is in the domain of \(g\) and \(g(x)\) is in the domain of \(f\).

It is important to realize that the product of functions \(fg\) is not the same as the function composition \(f(g(x))\), because, in general, \(f(x)g(x){\neq}f(g(x))\).

Finding the Domain of a Composite Function

As we discussed previously, the domain of a composite function such as \(f{\circ}g\) is dependent on the domain of \(g\) and the domain of \(f\). It is important to know when we can apply a composite function and when we cannot, that is, to know the domain of a function such as \(f{\circ}g\). Let us assume we know the domains of the functions \(f\) and \(g\) separately. If we write the composite function for an input \(x\) as \(f(g(x))\), we can see right away that \(x\) must be a member of the domain of g in order for the expression to be meaningful, because otherwise we cannot complete the inner function evaluation. However, we also see that \(g(x)\) must be a member of the domain of \(f\), otherwise the second function evaluation in \(f(g(x))\) cannot be completed, and the expression is still undefined. Thus the domain of \(f{\circ}g\) consists of only those inputs in the domain of \(g\) that produce outputs from \(g\) belonging to the domain of \(f\). Note that the domain of \(f\) composed with \(g\) is the set of all \(x\) such that \(x\) is in the domain of \(g\) and g(x)\) is in the domain of \(f\).

Definition: Domain of a Composite Function

The domain of a composite function \(f(g(x))\) is the set of those inputs \(x\) in the domain of \(g\) for which \(g(x)\) is in the domain of \(f\).

How To...

Given a function composition \(f(g(x))\), determine its domain.

1. Find the domain of \(g\).
2. Find the domain of \(f\).
3. Find those inputs \(x\) in the domain of \(g\) for which \(g(x)\) is in the domain of \(f\). That is, exclude those inputs \(x\) from the domain of \(g\) for which \(g(x)\) is not in the domain of \(f\). The resulting set is the domain of \(f{\circ}g\).

Example \(\PageIndex{8A}\): Finding the Domain of a Composite Function

Find the domain of

\[(f∘g)(x) \text{ where } f(x)=\dfrac{5}{x−1} \text{ and } g(x)=\dfrac{4}{3x−2} \nonumber\]

Solution

The domain of \(g(x)\) consists of all real numbers except \(x=\frac{2}{3}\), since that input value would cause us to divide by 0. Likewise, the domain of \(f\) consists of all real numbers except 1. So we need to exclude from the domain of \(g(x)\) that value of \(x\) for which \(g(x)=1\).

\[\begin{align*} \dfrac{4}{3x-2}&= 1 \\[4pt] 4 &=3x-2 \\[4pt] 6&=3x \\[4pt] x&= 2 \end{align*}\]

So the domain of \(f{\circ}g\) is the set of all real numbers except \(\frac{2}{3}\) and \(2\). This means that

\[x{\neq} \dfrac{2}{3} \text{ or } x\neq2 \nonumber\]

We can write this in interval notation as

\[\left(−\infty,\dfrac{2}{3}\right)\cup \left(\dfrac{2}{3},2 \right)\cup \left(2,\infty \right) \nonumber\]