2.1: Linear Functions

Representing Linear Functions

The function describing the train’s motion is a linear function, which is defined as a function with a constant rate of change, that is, a polynomial of degree 1. There are several ways to represent a linear function, including word form, function notation, tabular form, and graphical form. We will describe the train’s motion as a function using each method.

Representing a Linear Function in Word Form

Let’s begin by describing the linear function in words. For the train problem we just considered, the following word sentence may be used to describe the function relationship.

• The train’s distance from the station is a function of the time during which the train moves at a constant speed plus its original distance from the station when it began moving at constant speed.

The speed is the rate of change. Recall that a rate of change is a measure of how quickly the dependent variable changes with respect to the independent variable. The rate of change for this example is constant, which means that it is the same for each input value. As the time (input) increases by 1 second, the corresponding distance (output) increases by 83 meters. The train began moving at this constant speed at a distance of 250 meters from the station.

Representing a Linear Function in Function Notation

Another approach to representing linear functions is by using function notation. One example of function notation is an equation written in the form known as the slope-intercept form of a line, where xis the input value, \(m\) is the rate of change, and \(b\) is the initial value of the dependent variable.

\[\begin{align*} &\text{Equation form } &y=mx+b \\[4pt] &\text{Equation notation } &f(x)=mx+b \end{align*}\]

In the example of the train, we might use the notation \(D(t)\) in which the total distance \(D\) is a function of the time \(t\). The rate, \(m\), is 83 meters per second. The initial value of the dependent variable \(b\) is the original distance from the station, 250 meters. We can write a generalized equation to represent the motion of the train.

\[D(t)=83t+250\]

Representing a Linear Function in Tabular Form

A third method of representing a linear function is through the use of a table. The relationship between the distance from the station and the time is represented in Figure \(\PageIndex{2}\). From the table, we can see that the distance changes by 83 meters for every 1 second increase in time.

Figure \(\PageIndex{2}\): Tabular representation of the function \(D\) showing selected input and output values

Q/A? Can the input in the previous example be any real number?

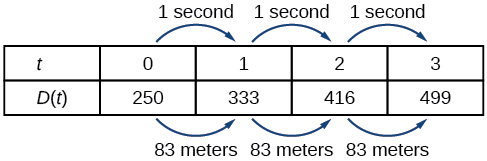
No. The input represents time, so while nonnegative rational and irrational numbers are possible, negative real numbers are not possible for this example. The input consists of non-negative real numbers.

Representing a Linear Function in Graphical Form

Another way to represent linear functions is visually, using a graph. We can use the function relationship from above, \(D(t)=83t+250\), to draw a graph, represented in Figure \(\PageIndex{3}\). Notice the graph is a line. When we plot a linear function, the graph is always a line.

The rate of change, which is constant, determines the slant, or slope of the line. The point at which the input value is zero is the vertical intercept, or y-intercept, of the line. We can see from the graph in Figure \(\PageIndex{3}\) that the y-intercept in the train example we just saw is \((0,250)\) and represents the distance of the train from the station when it began moving at a constant speed.

Figure \(\PageIndex{3}\): The graph of \(D(t)=83t+250\). Graphs of linear functions are lines because the rate of change is constant.

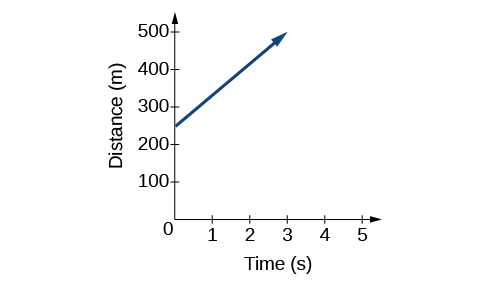
Notice that the graph of the train example is restricted, but this is not always the case. Consider the graph of the line \(f(x)=2x+1\). Ask yourself what numbers can be input to the function, that is, what is the domain of the function? The domain is comprised of all real numbers because any number may be doubled, and then have one added to the product.

Definition: Linear Function

A linear function is a function whose graph is a line. Linear functions can be written in the slope-intercept form of a line

\[f(x)=mx+b\]

where \(b\) is the initial or starting value of the function (when input, \(x=0\)), and \(m\) is the constant rate of change, or slope of the function. The y-intercept is at \((0,b)\).

Example \(\PageIndex{1}\): Using a Linear Function to Find the Pressure on a Diver

The pressure, \(P\), in pounds per square inch (PSI) on the diver in Figure \(\PageIndex{4}\) depends upon her depth below the water surface, \(d\), in feet. This relationship may be modeled by the equation, \(P(d)=0.434d+14.696\). Restate this function in words.

Figure \(\PageIndex{4}\): (credit: Ilse Reijs and Jan-Noud Hutten)Hutten)

To restate the function in words, we need to describe each part of the equation. The pressure as a function of depth equals four hundred thirty-four thousandths times depth plus fourteen and six hundred ninety-six thousandths.

Analysis

The initial value, 14.696, is the pressure in PSI on the diver at a depth of 0 feet, which is the surface of the water. The rate of change, or slope, is 0.434 PSI per foot. This tells us that the pressure on the diver increases 0.434 PSI for each foot her depth increases.

Determining whether a Linear Function Is Increasing, Decreasing, or Constant

The linear functions we used in the two previous examples increased over time, but not every linear function does. A linear function may be increasing, decreasing, or constant. For an increasing function, as with the train example, the output values increase as the input values increase. The graph of an increasing function has a positive slope. A line with a positive slope slants upward from left to right as in Figure \(\PageIndex{5}\)(a). For a decreasing function, the slope is negative. The output values decrease as the input values increase. A line with a negative slope slants downward from left to right as in Figure \(\PageIndex{5}\)(b). If the function is constant, the output values are the same for all input values so the slope is zero. A line with a slope of zero is horizontal as in Figure \(\PageIndex{5}\)(c).

Figure \(\PageIndex{5}\): Three graphs depicting an increasing function, a decreasing function, and a constant function.]
Increasing and Decreasing Functions

Increasing and Decreasing Functions

The slope determines if the function is an increasing linear function, a decreasing linear function, or a constant function.

• \(f(x)=mx+b\) is an increasing function if \(m>0\).
• \(f(x)=mx+b\) is an decreasing function if \(m<0\).
• \(f(x)=mx+b\) is a constant function if \(m=0\).

Example \(\PageIndex{2}\): Deciding whether a Function Is Increasing, Decreasing, or Constant

Some recent studies suggest that a teenager sends an average of 60 texts per day. For each of the following scenarios, find the linear function that describes the relationship between the input value and the output value. Then, determine whether the graph of the function is increasing, decreasing, or constant.

1. The total number of texts a teen sends is considered a function of time in days. The input is the number of days, and output is the total number of texts sent.
2. A teen has a limit of 500 texts per month in his or her data plan. The input is the number of days, and output is the total number of texts remaining for the month.
3. A teen has an unlimited number of texts in his or her data plan for a cost of $50 per month. The input is the number of days, and output is the total cost of texting each month.

Solution

Analyze each function.

1. The function can be represented as \(f(x)=60x\) where \(x\) is the number of days. The slope, 60, is positive so the function is increasing. This makes sense because the total number of texts increases with each day.
2. The function can be represented as \(f(x)=500−60x\) where \(x\) is the number of days. In this case, the slope is negative so the function is decreasing. This makes sense because the number of texts remaining decreases each day and this function represents the number of texts remaining in the data plan after \(x\) days.
3. The cost function can be represented as \(f(x)=50\) because the number of days does not affect the total cost. The slope is 0 so the function is constant.

Calculating and Interpreting Slope

In the examples we have seen so far, we have had the slope provided for us. However, we often need to calculate the slope given input and output values. Given two values for the input, \(x_1\) and \(x_2\), and two corresponding values for the output, \(y_1\) and \(y_2\)—which can be represented by a set of points, \((x_1,y_1)\) and \((x_2,y_2)\)—we can calculate the slope \(m\), as follows

\[\begin{align*} m &= \dfrac{\text{change in output (rise)}}{ \text{change in input (run)}} \\[4pt] &= \dfrac{{\Delta}y}{ {\Delta}x} = \dfrac{y_2−y_1}{x_2−x_1} \end{align*}\]

where \({\Delta}y\) is the vertical displacement and \({\Delta}x\) is the horizontal displacement. Note in function notation two corresponding values for the output \(y_1\) and \(y_2\) for the function \(f\), \(y_1=f(x_1)\) and \(y_2=f(x_2)\), so we could equivalently write

\[m=\dfrac{f(x_2)-f(x_1)}{x_2-x_1} \nonumber\]

Figure \(\PageIndex{6}\) indicates how the slope of the line between the points, \((x_1,y_1)\) and \((x_2,y_2)\), is calculated. Recall that the slope measures steepness. The greater the absolute value of the slope, the steeper the line is.

Figure \(\PageIndex{6}\): The slope of a function is calculated by the change in \(y\) divided by the change in \(x\). It does not matter which coordinate is used as the \((x_2,y_2)\) and which is the \((x_1 ,y_1)\),as long as each calculation is started with the elements from the same coordinate pair.

Q & A

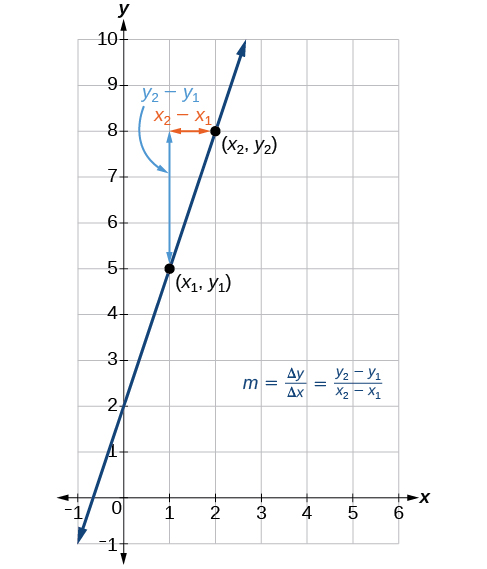
Are the units for slope always \(\frac{\text{units for the output}}{ \text{units for the input}}\)?

Yes. Think of the units as the change of output value for each unit of change in input value. An example of slope could be miles per hour or dollars per day. Notice the units appear as a ratio of units for the output per units for the input.

Calculate Slope

The slope, or rate of change, of a function \(m\) can be calculated according to the following:

\[m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{{\Delta}y}{{\Delta}x}=\dfrac{y_2-y_1}{x_2-x_1}\]

where \(x_1\) and \(x_2\) are input values, \(y_1\) and \(y_2\) are output values.

Writing the Point-Slope Form of a Linear Equation

Up until now, we have been using the slope-intercept form of a linear equation to describe linear functions. Here, we will learn another way to write a linear function, the point-slope form.

\[y-y_1=m(x-x_1)\]

The point-slope form is derived from the slope formula.

\[ \begin{align*} &m=\dfrac{y-y_1}{x-x_1} &\text{assuming }x{\neq}x_1 \\ &m(x-x_1)=\dfrac{y-y_1}{x-x_1}(x-x_1) &\text{Multiply both sides by }(x-x_1). \\ &m(x-x_1)=y-y_1 &\text{Simplify} \\ &y-y_1=m(x-x_1) &\text{Rearrange} \end{align*}\]

Keep in mind that the slope-intercept form and the point-slope form can be used to describe the same function. We can move from one form to another using basic algebra. For example, suppose we are given an equation in point-slope form, \(y−4=− \frac{1}{2}(x−6)\). We can convert it to the slope-intercept form as shown.

\[\begin{align*} y-4&=-\dfrac{1}{2}(x-6) \\ y-4&=-\dfrac{1}{2}x+3 &\text{Distribute the }-\dfrac{1}{2}. \\ y&=-\dfrac{1}{2}x+7 &\text{Add 4 to each side.}\end{align*}\]

Therefore, the same line can be described in slope-intercept form as \(y=\dfrac{1}{2}x+7\).

Point-Slope Form of a Linear Equation

The point-slope form of a linear equation takes the form

\[y-y_1=m(x−x_1)\]

where \(m\) is the slope, \(x_1\) and \(y_1\) are the \(x\) and \(y\) coordinates of a specific point through which the line passes.

Writing the Equation of a Line Using a Point and the Slope

The point-slope form is particularly useful if we know one point and the slope of a line. Suppose, for example, we are told that a line has a slope of 2 and passes through the point \((4,1)\). We know that \(m=2\) and that \(x_1=4\) and \(y_1=1\). We can substitute these values into the general point-slope equation.

\[\begin{align*} y−y_1&=m(x−x_1) \\ y−1&=2(x−4) \end{align*}\]

If we wanted to then rewrite the equation in slope-intercept form, we apply algebraic techniques.

\[\begin{align*} y−1&=2(x−4) \\ y−1&=2x−8 &\text{Distribute the 2.} \\ y&=2x−7 &\text{Add 1 to each side.} \end{align*}\]

Both equations, \(y−1=2(x−4)\) and \(y=2x–7\), describe the same line. See Figure \(\PageIndex{7}\).

Figure \(\PageIndex{7}\)

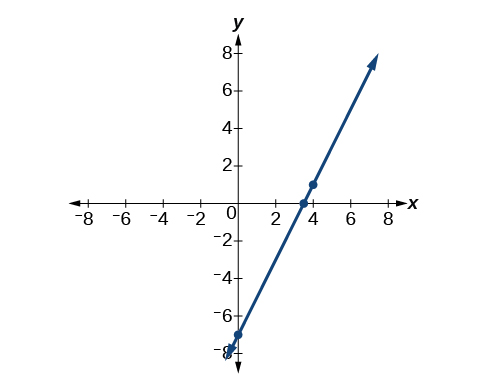
Writing the Equation of a Line Using Two Points

The point-slope form of an equation is also useful if we know any two points through which a line passes. Suppose, for example, we know that a line passes through the points \((0, 1)\) and \((3, 2)\). We can use the coordinates of the two points to find the slope.

\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{2-1}{3-0} \\ &=\dfrac{1}{3} \end{align*}\]

Now we can use the slope we found and the coordinates of one of the points to find the equation for the line. Let use \((0,1)\) for our point.

\[\begin{align*} y-y_1&=m(x-x_1) \\ y-1&=\dfrac{1}{3}(x-0) \end{align*}\]

As before, we can use algebra to rewrite the equation in the slope-intercept form.

\[\begin{align*} y-1&=\dfrac{1}{3}(x-0) \\ y-1&=\dfrac{1}{3}x &\text{Distribute the }\dfrac{1}{3}. \\ y&=\dfrac{1}{3}x+1 &\text{Add 1 to each side.} \end{align*}\]

Both equations describe the line shown in Figure \(\PageIndex{8}\).

Figure \(\PageIndex{8}\)

Example \(\PageIndex{6}\): Writing Linear Equations Using Two Points

Write the point-slope form of an equation of a line that passes through the points \((5,1)\) and \((8, 7)\). Then rewrite it in the slope-intercept form.

Let’s begin by finding the slope.

\[\begin{align*} m&=\dfrac{y_2-y_1}{x_2-x_1} \\ &=\dfrac{7-1}{8-5} \\ &=\dfrac{6}{3} \\ &= 2 \end{align*}\]

So \(m=2\). Next, we substitute the slope and the coordinates for one of the points into the general point-slope equation. We can choose either point, but we will use \((5,1)\).

\[\begin{align*} y-y_1&=m(x-x_1) \\ y-1&=2(x-5) \end{align*}\]

The point-slope equation of the line is \(y_2–1=2(x_2–5)\). To rewrite the equation in slope-intercept form, we use algebra.

\[\begin{align*} y-1&=2(x-5) \\ y-1&=2x-10 \\ y&=2x-9 \end{align*}\]

The slope-intercept equation of the line is \(y=2x–9\).