6.3: Inverse Trigonometric Functions

Understanding and Using the Inverse Sine, Cosine, and Tangent Functions

In order to use inverse trigonometric functions, we need to understand that an inverse trigonometric function “undoes” what the original trigonometric function “does,” as is the case with any other function and its inverse. In other words, the domain of the inverse function is the range of the original function, and vice versa, as summarized in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\)

For example, if \(f(x)=\sin\space x\), then we would write \(f^{−1}(x)={\sin}^{−1}x\). Be aware that \({\sin}^{−1}x\) does not mean \(\dfrac{1}{\sin\space x}\). The following examples illustrate the inverse trigonometric functions:

• Since \(\sin\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}\), then \(\dfrac{\pi}{6}={\sin}^{−1}\left(\dfrac{1}{2}\right)\).
• Since \(\cos(\pi)=−1\), then \(\pi={\cos}^{−1}(−1)\).
• Since \(\tan\left (\dfrac{\pi}{4}\right )=1\), then \(\dfrac{\pi}{4}={\tan}^{−1}(1)\).

In previous sections, we evaluated the trigonometric functions at various angles, but at times we need to know what angle would yield a specific sine, cosine, or tangent value. For this, we need inverse functions. Recall that, for a one-to-one function, if \(f(a)=b\), then an inverse function would satisfy \(f^{−1}(b)=a\).

Bear in mind that the sine, cosine, and tangent functions are not one-to-one functions. The graph of each function would fail the horizontal line test. In fact, no periodic function can be one-to-one because each output in its range corresponds to at least one input in every period, and there are an infinite number of periods. As with other functions that are not one-to-one, we will need to restrict the domain of each function to yield a new function that is one-to-one. We choose a domain for each function that includes the number 0. Figure \(\PageIndex{2}\) shows the graph of the sine function limited to \(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\) and the graph of the cosine function limited to \([ 0,\pi ]\).

Figure \(\PageIndex{2}\): (a) Sine function on a restricted domain of \(\left[ −\dfrac{\pi}{2}, \dfrac{\pi}{2} \right]\); (b) Cosine function on a restricted domain of \([ 0,\pi ]\)

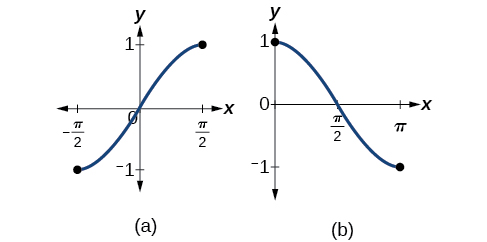
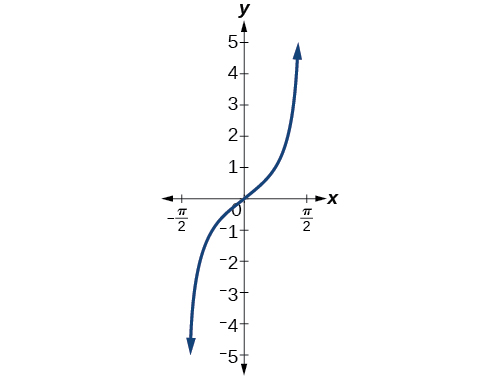
Figure \(\PageIndex{3}\) shows the graph of the tangent function limited to \(\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\).

Figure \(\PageIndex{3}\): Tangent function on a restricted domain of \(\left (−\dfrac{\pi}{2},\dfrac{\pi}{2}\right )\)

These conventional choices for the restricted domain are somewhat arbitrary, but they have important, helpful characteristics. Each domain includes the origin and some positive values, and most importantly, each results in a one-to-one function that is invertible. The conventional choice for the restricted domain of the tangent function also has the useful property that it extends from one vertical asymptote to the next instead of being divided into two parts by an asymptote.

On these restricted domains, we can define the inverse trigonometric functions.

• The inverse sine function \(y={\sin}^{−1}x\) means \(x=\sin\space y\). The inverse sine function is sometimes called the arcsine function, and notated \(\arcsin\space x\).

  \(y={\sin}^{−1}x\) has domain \([−1,1]\) and range \(\left[−\frac{\pi}{2},\frac{\pi}{2}\right]\)

• The inverse cosine function \(y={\cos}^{−1}x\) means \(x=\cos\space y\). The inverse cosine function is sometimes called the arccosine function, and notated \(\arccos\space x\).

  \(y={\cos}^{−1}x\) has domain \([−1,1]\) and range \([0,π]\)

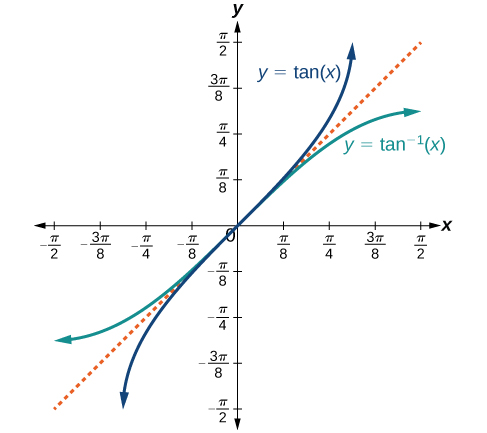
• The inverse tangent function \(y={\tan}^{−1}x\) means \(x=\tan\space y\). The inverse tangent function is sometimes called the arctangent function, and notated \(\arctan\space x\).

  \(y={\tan}^{−1}x\) has domain \((−\infty,\infty)\) and range \(\left(−\frac{\pi}{2},\frac{\pi}{2}\right)\)

The graphs of the inverse functions are shown in Figures \(\PageIndex{4}\) - \(\PageIndex{6}\). Notice that the output of each of these inverse functions is a number, an angle in radian measure. We see that \({\sin}^{−1}x\) has domain \([ −1,1 ]\) and range \(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\), \({\cos}^{−1}x\) has domain \([ −1,1 ]\) and range \([0,\pi]\), and \({\tan}^{−1}x\) has domain of all real numbers and range \(\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\). To find the domain and range of inverse trigonometric functions, switch the domain and range of the original functions. Each graph of the inverse trigonometric function is a reflection of the graph of the original function about the line \(y=x\).

Figure \(\PageIndex{4}\): The sine function and inverse sine (or arcsine) function

Figure \(\PageIndex{5}\): The cosine function and inverse cosine (or arccosine) function

Figure \(\PageIndex{6}\): The tangent function and inverse tangent (or arctangent) function

RELATIONS FOR INVERSE SINE, COSINE, AND TANGENT FUNCTIONS

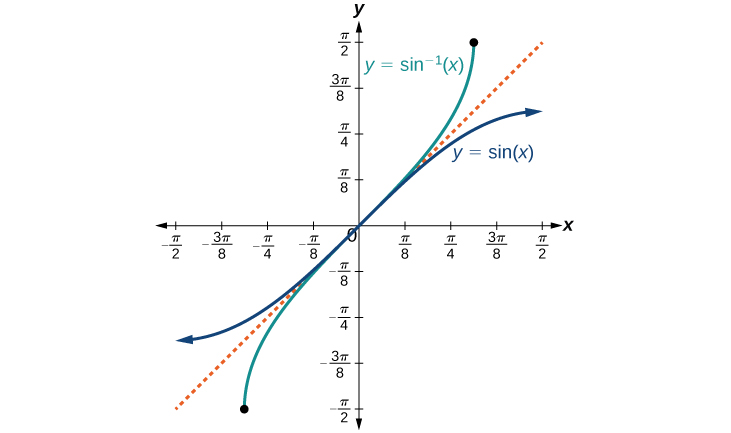
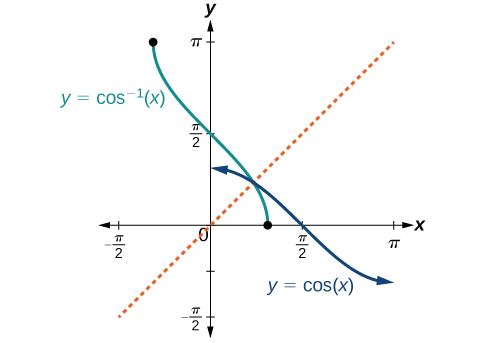
For angles in the interval \(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\), if \(\sin y=x\), then \({\sin}^{−1}x=y\).

For angles in the interval \([ 0,\pi ]\), if \(\cos y=x\), then \({\cos}^{−1}x=y\).

For angles in the interval \(\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right )\), if \(\tan y=x\),then \({\tan}^{−1}x=y\).

Finding the Exact Value of Expressions Involving the Inverse Sine, Cosine, and Tangent Functions

Now that we can identify inverse functions, we will learn to evaluate them. For most values in their domains, we must evaluate the inverse trigonometric functions by using a calculator, interpolating from a table, or using some other numerical technique. Just as we did with the original trigonometric functions, we can give exact values for the inverse functions when we are using the special angles, specifically \(\dfrac{\pi}{6}\)(30°), \(\dfrac{\pi}{4}\)(45°), and \(\dfrac{\pi}{3}\)(60°), and their reflections into other quadrants.

Given a “special” input value, evaluate an inverse trigonometric function.

1. Find angle \(x\) for which the original trigonometric function has an output equal to the given input for the inverse trigonometric function.
2. If \(x\) is not in the defined range of the inverse, find another angle \(y\) that is in the defined range and has the same sine, cosine, or tangent as \(x\),depending on which corresponds to the given inverse function.

Finding Exact Values of Composite Functions with Inverse Trigonometric Functions

There are times when we need to compose a trigonometric function with an inverse trigonometric function. In these cases, we can usually find exact values for the resulting expressions without resorting to a calculator. Even when the input to the composite function is a variable or an expression, we can often find an expression for the output. To help sort out different cases, let \(f(x)\) and \(g(x)\) be two different trigonometric functions belonging to the set{ \(\sin(x)\),\(\cos(x)\),\(\tan(x)\) } and let \(f^{-1}(y)\) and \(g^{-1}(y)\) be their inverses.

Evaluating Compositions of the Form \(f(f^{-1}(y))\) and \(f^{-1}(f(x))\)

For any trigonometric function,\(f(f^{-1}(y))=y\) for all \(y\) in the proper domain for the given function. This follows from the definition of the inverse and from the fact that the range of \(f\) was defined to be identical to the domain of \(f^{−1}\). However, we have to be a little more careful with expressions of the form \(f^{-1}(f(x))\).

COMPOSITIONS OF A TRIGONOMETRIC FUNCTION AND ITS INVERSE

\[\begin{align*} \sin({\sin}^{-1}x)&= x\qquad \text{for } -1\leq x\leq 1\\ \cos({\cos}^{-1}x)&= x\qquad \text{for } -1\leq x\leq 1\\ \tan({\tan}^{-1}x)&= x\qquad \text{for } -\infty<x<\infty\\ {\sin}^{-1}(\sin x)&= x\qquad \text{only for } -\dfrac{\pi}{2}\leq x\leq \dfrac{\pi}{2}\\ {\cos}^{-1}(\cos x)&= x\qquad \text{only for } 0\leq x\leq \pi\\ {\tan}^{-1}(\tan x)& =x\qquad \text{only for } -\dfrac{\pi}{2}< x< \dfrac{\pi}{2} \end{align*}\]

Given an expression of the form \(f^{-1}(f(\theta))\) where \(f(\theta)=\sin \theta\), \(\cos \theta\), or \(\tan \theta\), evaluate.

1. If \(\theta\) is in the restricted domain of \(f\), then \(f^{−1}(f(\theta))=\theta\).
2. If not, then find an angle \(\phi\) within the restricted domain off f such that \(f(\phi)=f(\theta)\). Then \(f^{−1}(f(\theta))=\phi\).