7.2: Sum and Difference Identities
- Page ID
- 117155
Using the Sum and Difference Formulas for Cosine
Finding the exact value of the sine, cosine, or tangent of an angle is often easier if we can rewrite the given angle in terms of two angles that have known trigonometric values. We can use the special angles, which we can review in the unit circle shown in Figure \(\PageIndex{2}\).
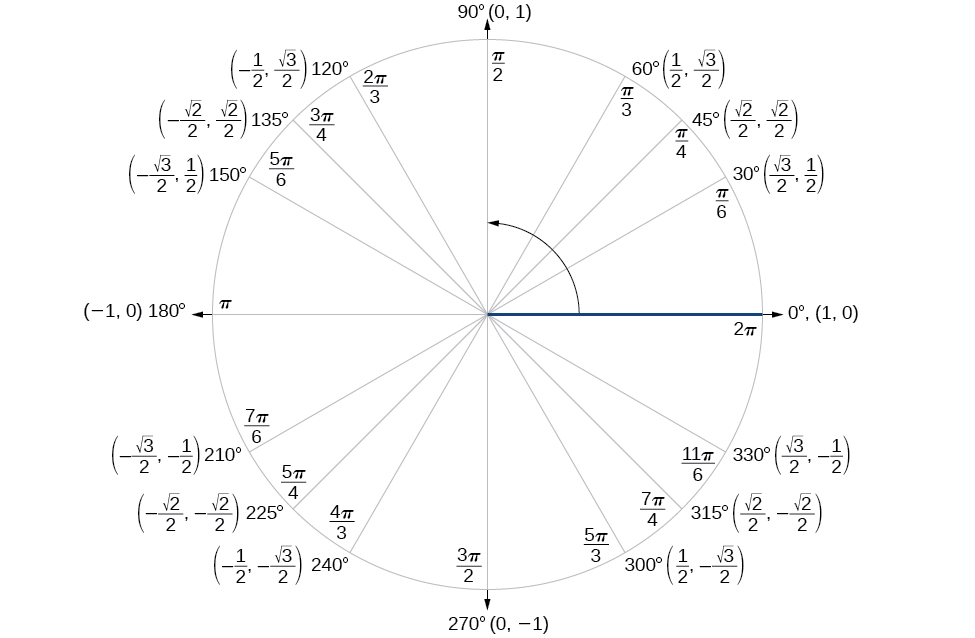
We will begin with the sum and difference formulas for cosine, so that we can find the cosine of a given angle if we can break it up into the sum or difference of two of the special angles (Table \(\PageIndex{1}\)).
| Sum formula for cosine | \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\) |
| Difference formula for cosine | \(\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
First, we will prove the difference formula for cosines. Let’s consider two points on the unit circle (Figure \(\PageIndex{3}\)). Point \(P\) is at an angle \(\alpha\) from the positive \(x\)-axis with coordinates \((\cos \alpha,\sin \alpha)\) and point \(Q\) is at an angle of \(\beta\) from the positive \(x\)-axis with coordinates \((\cos \beta,\sin \beta)\). Note the measure of angle \(POQ\) is \(\alpha−\beta\).
Label two more points: \(A\) at an angle of \((\alpha−\beta)\) from the positive \(x\)-axis with coordinates \((\cos(\alpha−\beta),\sin(\alpha−\beta))\); and point \(B\) with coordinates \((1,0)\). Triangle \(POQ\) is a rotation of triangle \(AOB\) and thus the distance from \(P\) to \(Q\) is the same as the distance from \(A\) to \(B\).
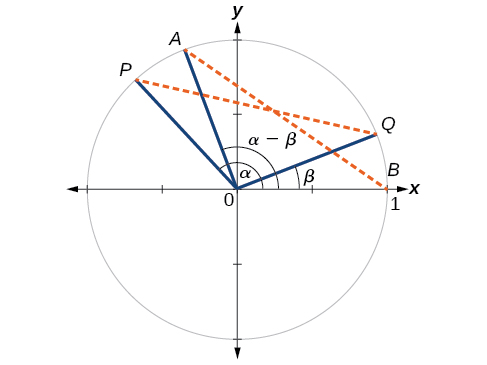
We can find the distance from \(P\) to \(Q\) using the distance formula.
\[\begin{align*}
d_{PQ}&= \sqrt{{(\cos \alpha - \cos \beta )}^2+{(sin \alpha - sin \beta )}^2}\\[4pt]
&= \sqrt{{\cos}^2 \alpha-2\cos \alpha \cos \beta+{\cos}^2 \beta+{\sin}^2 \alpha-2\sin \alpha \sin \beta+{\sin}^2 \beta} & & \text {Apply Pythagorean identity and simplify.}\\[4pt]
&= \sqrt{({\cos}^2 \alpha+{\sin}^2 \alpha)+({\cos}^2 \beta+{\sin}^2 \beta)-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta}\\[4pt]
&= \sqrt{1+1-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta}\\[4pt]
&= \sqrt{2-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta}\end{align*}\]
Similarly, using the distance formula we can find the distance from \(A\) to \(B\).
\[\begin{align*}
d_{AB}&= \sqrt{{(\cos(\alpha-\beta)-1)}^2+{(\sin(\alpha-\beta)-0)}^2}\\[4pt]
&= \sqrt{{\cos}^2(\alpha-\beta)-2\cos(\alpha-\beta)+1+{\sin}^2(\alpha-\beta)} & & \text {Apply Pythagorean identity and simplify}\\[4pt]
&= \sqrt{({\cos}^2(\alpha-\beta)+{\sin}^2(\alpha-\beta))-2\cos(\alpha-\beta)+1}\\[4pt]
&= \sqrt{1-2\cos(\alpha-\beta)+1}\\[4pt]
&= \sqrt{2-2\cos(\alpha-\beta)} & & \text {Subtract 2 from both sides and divide both sides by −2.}\\[4pt]
\cos \alpha \cos \beta+\sin \alpha \sin \beta&= \cos(\alpha-\beta)
\end{align*}\]
Thus, we have the difference formula for cosine. We can use similar methods to derive the cosine of the sum of two angles.
These formulas can be used to calculate the cosine of sums and differences of angles.
\[\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\]
\[\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\]
- Write the difference formula for cosine.
- Substitute the values of the given angles into the formula.
- Simplify.
Using the formula for the cosine of the difference of two angles, find the exact value of \(\cos\left(\dfrac{5\pi}{4}−\dfrac{\pi}{6}\right)\).
Solution
Begin by writing the formula for the cosine of the difference of two angles. Then substitute the given values.
\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos\left(\dfrac{5\pi}{4}-\dfrac{\pi}{6}\right)&= \cos\left(\dfrac{5\pi}{4}\right)\cos\left(\dfrac{\pi}{6}\right)+\sin\left(\dfrac{5\pi}{4}\right)\sin\left(\dfrac{\pi}{6}\right)\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{\sqrt{3}}{2}\right)-\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{1}{2}\right)\\[4pt] &= -\dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{-\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Keep in mind that we can always check the answer using a graphing calculator in radian mode.
Using the Sum and Difference Formulas for Sine
The sum and difference formulas for sine can be derived in the same manner as those for cosine, and they resemble the cosine formulas.
These formulas can be used to calculate the sines of sums and differences of angles.
\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\]
\[\sin(\alpha−\beta)=\sin \alpha \cos \beta−\cos \alpha \sin \beta\]
- Write the difference formula for sine.
- Substitute the given angles into the formula.
- Simplify.
Use the sum and difference identities to evaluate the difference of the angles and show that part a equals part b.
- \(\sin(45°−30°)\)
- \(\sin(135°−120°)\)
Solution
- Let’s begin by writing the formula and substitute the given angles.
\[\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(45^{\circ}-30^{\circ})&= \sin(45^{\circ})\cos(30^{\circ})-\cos(45^{\circ})\sin(30^{\circ}) \end{align*}\]
Next, we need to find the values of the trigonometric expressions.
\(\sin(45°)=\frac{\sqrt{2}}{2}, \qquad \cos(30°)=\frac{\sqrt{3}}{2}, \qquad \cos(45°)=\frac{\sqrt{2}}{2}, \qquad \sin(30°)=\frac{1}{2}\)
Now we can substitute these values into the equation and simplify.
\[\begin{align*} \sin(45°-30°)&= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
- Again, we write the formula and substitute the given angles.
\[\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(135^{\circ}-120^{\circ})&= \sin(135^{\circ})\cos(120^{\circ})-\cos(135^{\circ})\sin(120^{\circ}) \end{align*}\]
Next, we find the values of the trigonometric expressions.
\(\sin(135°)=\frac{\sqrt{2}}{2}, \qquad \cos(120°)=-\frac{1}{2}, \qquad \cos(135°)=\frac{\sqrt{2}}{2}, \qquad \sin(120°)=\frac{\sqrt{3}}{2}\)
Now we can substitute these values into the equation and simplify.
\[\begin{align*} \sin(135^{\circ}-120^{\circ})&= \dfrac{\sqrt{2}}{2}\left(-\dfrac{1}{2}\right)-\left(-\dfrac{\sqrt{2}}{2}\right)\left (\dfrac{\sqrt{3}}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Using the Sum and Difference Formulas for Tangent
Finding exact values for the tangent of the sum or difference of two angles is a little more complicated, but again, it is a matter of recognizing the pattern.
Finding the sum of two angles formula for tangent involves taking quotient of the sum formulas for sine and cosine and simplifying. Recall, \(\tan x=\dfrac{\sin x}{\cos x}\), when \(\cos x≠0\).
Let’s derive the sum formula for tangent.
\[\begin{align*}
\tan\left (\alpha+\beta\right)&= \dfrac{\sin\left (\alpha+\beta\right )}{\cos(\alpha+\beta)}\\[6pt]
&= \dfrac{\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\cos \alpha \cos \beta-\sin \alpha \sin \beta}\\[6pt]
&= \dfrac{\dfrac{\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{\dfrac{\cos \alpha \cos \beta-\sin \alpha \sin \beta}{\cos \alpha \cos \beta}}\\[6pt]
&= \dfrac{\dfrac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta}+\dfrac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{\dfrac{\cos \alpha \cos \beta}{\cos \alpha \cos \beta}-\dfrac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}}\\[6pt]
&= \dfrac{\dfrac{\sin \alpha}{\cos \alpha}+\dfrac{\sin \beta}{\cos \beta}}{1-\dfrac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}}\\[6pt]
&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}
\end{align*}\]
We can derive the difference formula for tangent in a similar way.
The sum and difference formulas for tangent are:
\[\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1−\tan \alpha \tan \beta}\]
\[\tan(\alpha-\beta)=\dfrac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}\]
- Write the sum formula for tangent.
- Substitute the given angles into the formula.
- Simplify.
Find the exact value of \(\tan\left(\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)\).
Solution
Let’s first write the sum formula for tangent and then substitute the given angles into the formula.
\[\begin{align*}
\tan(\alpha+\beta)&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta} \\[4pt]
\tan\left(\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)&= \dfrac{\tan\left (\dfrac{\pi}{6}\right)+\tan\left (\dfrac{\pi}{4}\right )}{1-\left (\tan\left (\dfrac{\pi}{6}\right ) \right )\left (\tan\left (\dfrac{\pi}{4}\right )\right )}\end{align*}\]
Next, we determine the individual function values within the formula:
\[\tan\left (\dfrac{\pi}{6}\right )= \dfrac{1}{\sqrt{3}}, \quad \text{and} \quad \tan\left (\dfrac{\pi}{4}\right) = 1\]
So we have,
\[\begin{align*}\tan\left (\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)&= \dfrac{\dfrac{1}{\sqrt{3}}+1}{1-\left(\dfrac{1}{\sqrt{3}}\right )(1)}\\[6pt]
&= \dfrac{\dfrac{1+\sqrt{3}}{\sqrt{3}}}{\dfrac{\sqrt{3}-1}{\sqrt{3}}}\\[6pt]
&= \dfrac{1+\sqrt{3}}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{\sqrt{3}-1}\\[6pt]
&= \dfrac{\sqrt{3}+1}{\sqrt{3}-1}
\end{align*}\]
Using Sum and Difference Formulas for Cofunctions
Now that we can find the sine, cosine, and tangent functions for the sums and differences of angles, we can use them to do the same for their cofunctions. You may recall from Right Triangle Trigonometry that, if the sum of two positive angles is \(\frac{\pi}{2}\), those two angles are complements, and the sum of the two acute angles in a right triangle is \(\frac{\pi}{2}\), so they are also complements. In Figure \(\PageIndex{6}\), notice that if one of the acute angles is labeled as \(\theta\), then the other acute angle must be labeled \(\frac{\pi}{2}−\theta\).
Notice also that \(\sin \theta=\cos\left(\frac{\pi}{2}−\theta\right)\),which is opposite over hypotenuse. Thus, when two angles are complimentary, we can say that the sine of \(\theta\) equals the cofunction of the complement of \(\theta\). Similarly, tangent and cotangent are cofunctions, and secant and cosecant are cofunctions.
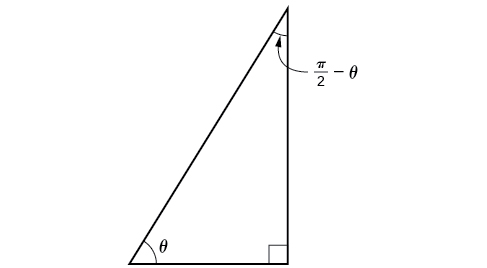
From these relationships, the cofunction identities are formed. Recall that you first encountered these identities in The Unit Circle: Sine and Cosine Functions.
The cofunction identities are summarized in Table \(\PageIndex{2}\).
| \(\sin \theta=\cos\left(\dfrac{\pi}{2}−\theta\right)\) | \(\cos \theta=\sin\left(\dfrac{\pi}{2}−\theta\right)\) |
| \(\tan \theta=\cot\left(\dfrac{\pi}{2}−\theta\right)\) | \(\cot \theta=\tan\left(\dfrac{\pi}{2}−\theta\right )\) |
| \(\sec \theta=\csc\left (\dfrac{\pi}{2}−\theta\right )\) | \(\csc \theta=\sec\left (\dfrac{\pi}{2}−\theta\right )\) |
Notice that the formulas in the table may also justified algebraically using the sum and difference formulas. For example, using
\(\cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\)
We can write
\[\begin{align*} \cos\left (\dfrac{\pi}{2}-\theta \right )&= \cos \dfrac{\pi}{2} \cos \theta+\sin \dfrac{\pi}{2} \sin \theta \\[4pt] &=(0)\cos \theta+(1)\sin \theta \\[4pt] &=\sin \theta \end{align*}\]
Write \(\tan \dfrac{\pi}{9}\) in terms of its cofunction.
Solution
The cofunction of \(\tan \theta=\cot\left (\dfrac{\pi}{2}−\theta\right )\). Thus,
\[\begin{align*} \tan\left (\dfrac{\pi}{9}\right )&= \cot\left (\dfrac{\pi}{2}-\dfrac{\pi}{9}\right )\\[4pt] &= \cot\left (\dfrac{9\pi}{18}-\dfrac{2\pi}{18}\right )\\[4pt] &= \cot\left (\dfrac{7\pi}{18}\right ) \end{align*}\]
Using the Sum and Difference Formulas to Verify Identities
Verifying an identity means demonstrating that the equation holds for all values of the variable. It helps to be very familiar with the identities or to have a list of them accessible while working the problems. Reviewing the general rules presented earlier may help simplify the process of verifying an identity.
- Begin with the expression on the side of the equal sign that appears most complex. Rewrite that expression until it matches the other side of the equal sign. Occasionally, we might have to alter both sides, but working on only one side is the most efficient.
- Look for opportunities to use the sum and difference formulas.
- Rewrite sums or differences of quotients as single quotients.
- If the process becomes cumbersome, rewrite the expression in terms of sines and cosines.
Verify the identity \(\sin(\alpha+\beta)+\sin(\alpha−\beta)=2\sin \alpha \cos \beta\).
Solution
We see that the left side of the equation includes the sines of the sum and the difference of angles.
\(\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\)
\(\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta\)
We can rewrite each using the sum and difference formulas.
\[\begin{align*} \sin(\alpha+\beta)+\sin(\alpha-\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta+\sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] &= 2\sin \alpha \cos \beta \end{align*}\]
We see that the identity is verified.
Verify the following identity.
\(\dfrac{\sin(\alpha−\beta)}{\cos \alpha \cos \beta}=\tan \alpha−\tan \beta\)
Solution
We can begin by rewriting the numerator on the left side of the equation.
\[\begin{align*} \dfrac{\sin(\alpha-\beta)}{\cos \alpha \cos \beta}&= \dfrac{\sin \alpha \cos \beta-\cos \alpha \sin \beta}{\cos \alpha \cos \beta}\\[4pt] &= \dfrac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta}-\dfrac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta} & & \text{Rewrite using a common denominator}\\[4pt] &= \dfrac{\sin \alpha}{\cos \alpha}-\dfrac{\sin \beta}{\cos \beta} & & \text{Cancel}\\[4pt] &= \tan \alpha-\tan \beta & & \text{Rewrite in terms of tangent} \end{align*}\]


