7.3: Double-Angle, Half-Angle, and Reduction Formulas

Using Double-Angle Formulas to Find Exact Values

In the previous section, we used addition and subtraction formulas for trigonometric functions. Now, we take another look at those same formulas. The double-angle formulas are a special case of the sum formulas, where \(\alpha=\beta\). Deriving the double-angle formula for sine begins with the sum formula,

\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\]

If we let \(\alpha=\beta=\theta\), then we have

\[\begin{align*} \sin(\theta+\theta)&= \sin \theta \cos \theta+\cos \theta \sin \theta\\[4pt] \sin(2\theta)&= 2\sin \theta \cos \theta \end{align*}\]

Deriving the double-angle for cosine gives us three options. First, starting from the sum formula, \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\),and letting \(\alpha=\beta=\theta\), we have

\[\begin{align*} \cos(\theta+\theta)&= \cos \theta \cos \theta-\sin \theta \sin \theta\\[4pt] \cos(2\theta)&= {\cos}^2 \theta - {\sin}^2 \theta \end{align*}\]

Using the Pythagorean properties, we can expand this double-angle formula for cosine and get two more variations. The first variation is:

\[\begin{align*} \cos(2\theta)&= {\cos}^2 \theta - {\sin}^2 \theta \\[4pt] &= (1-{\sin}^2 \theta)-{\sin}^2 \theta \end{align*}\]

The second variation is:

\[\begin{align*} \cos(2\theta)&= {\cos}^2 \theta-{\sin}^2 \theta\\[4pt] &= {\cos}^2 \theta-(1-{\cos}^2 \theta)\\[4pt] &= 2 {\cos}^2 \theta-1 \end{align*}\]

Similarly, to derive the double-angle formula for tangent, replacing \(\alpha=\beta=\theta\) in the sum formula gives

\[\begin{align*} \tan(\alpha+\beta)&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\\[4pt] \tan(\theta+\theta)&= \dfrac{\tan \theta+\tan \theta}{1-\tan \theta \tan \theta}\\[4pt] \tan(2\theta)&= \dfrac{2\tan \theta}{1-{\tan}^2 \theta} \end{align*}\]

DOUBLE-ANGLE FORMULAS

The double-angle formulas are summarized as follows:

\[\begin{align} \sin(2\theta)&= 2 \sin \theta \cos \theta\\[4pt] \cos(2\theta)&= {\cos}^2 \theta-{\sin}^2 \theta =1-2 {\sin}^2 \theta = 2{\cos}^2 \theta-1\\[4pt] \tan(2\theta)&= \dfrac{2 \tan \theta}{1-{\tan}^2\theta} \end{align}\]

How to: Given the tangent of an angle and the quadrant in which it is located, use the double-angle formulas to find the exact value

1. Draw a triangle to reflect the given information.
2. Determine the correct double-angle formula.
3. Substitute values into the formula based on the triangle.
4. Simplify.

Example \(\PageIndex{1}\): Using a Double-Angle Formula to Find the Exact Value Involving Tangent

Given that \(\tan \theta=−\dfrac{3}{4}\) and \(\theta\) is in quadrant II, find the following:

1. \(\sin(2\theta)\)
2. \(\cos(2\theta)\)
3. \(\tan(2\theta)\)

Solution

If we draw a triangle to reflect the information given, we can find the values needed to solve the problems on the image. We are given \(\tan \theta=−\dfrac{3}{4}\),such that \(\theta\) is in quadrant II. The tangent of an angle is equal to the opposite side over the adjacent side, and because \(\theta\) is in the second quadrant, the adjacent side is on the x-axis and is negative. Use the Pythagorean Theorem to find the length of the hypotenuse:

\[\begin{align*} {(-4)}^2+{(3)}^2&= c^2\\[4pt] 16+9&= c^2\\[4pt] 25&= c^2\\[4pt] c&= 5 \end{align*}\]

Now we can draw a triangle similar to the one shown in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\)

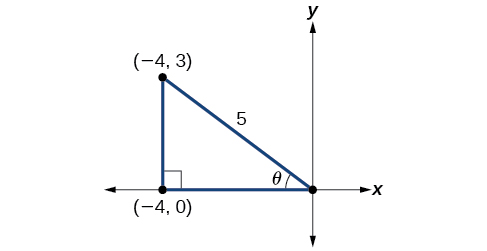
1. Let’s begin by writing the double-angle formula for sine.

   \(\sin(2\theta)=2 \sin \theta \cos \theta\)

   We see that we to need to find \(\sin \theta\) and \(\cos \theta\). Based on Figure \(\PageIndex{2}\), we see that the hypotenuse equals \(5\), so \(\sin θ=35\), \(\sin θ=35\), and \(\cos θ=−45\). Substitute these values into the equation, and simplify.

   Thus,

   \[\begin{align*} \sin(2\theta)&= 2\left(\dfrac{3}{5}\right)\left(-\dfrac{4}{5}\right)\\[4pt] &= -\dfrac{24}{25} \end{align*}\]

2. Write the double-angle formula for cosine.

   \(\cos(2\theta)={\cos}^2 \theta−{\sin}^2 \theta\)

   Again, substitute the values of the sine and cosine into the equation, and simplify.

   \[\begin{align*} \cos(2\theta)&= {\left(-\dfrac{4}{5}\right)}^2-{\left(\dfrac{3}{5}\right)}^2\\[4pt] &= \dfrac{16}{25}-\dfrac{9}{25}\\[4pt] &= \dfrac{7}{25} \end{align*}\]

3. Write the double-angle formula for tangent.

   \(\tan(2\theta)=\dfrac{2 \tan \theta}{1−{\tan}^2\theta}\)

   In this formula, we need the tangent, which we were given as \(\tan \theta=−\dfrac{3}{4}\). Substitute this value into the equation, and simplify.

   \[\begin{align*} \tan(2\theta)&= \dfrac{2\left(-\dfrac{3}{4}\right )}{1-{\left(-\dfrac{3}{4}\right)}^2}\\[4pt]
   &= \dfrac{-\dfrac{3}{2}}{1-\dfrac{9}{16}}\\[4pt]
   &= -\dfrac{3}{2}\left(\dfrac{16}{7}\right)\\[4pt]
   &= -\dfrac{24}{7}
   \end{align*}\]

Use Reduction Formulas to Simplify an Expression

The double-angle formulas can be used to derive the reduction formulas, which are formulas we can use to reduce the power of a given expression involving even powers of sine or cosine. They allow us to rewrite the even powers of sine or cosine in terms of the first power of cosine. These formulas are especially important in higher-level math courses, calculus in particular. Also called the power-reducing formulas, three identities are included and are easily derived from the double-angle formulas.

We can use two of the three double-angle formulas for cosine to derive the reduction formulas for sine and cosine. Let’s begin with \(\cos(2\theta)=1−2 {\sin}^2 \theta\). Solve for \({\sin}^2 \theta\):

\[\begin{align*} \cos(2\theta)&= 1-2 {\sin}^2 \theta\\[4pt] 2 {\sin}^2 \theta&= 1-\cos(2\theta)\\[4pt] {\sin}^2 \theta&= \dfrac{1-\cos(2\theta)}{2} \end{align*}\]

Next, we use the formula \(\cos(2\theta)=2 {\cos}^2 \theta−1\). Solve for \({\cos}^2 \theta\):

\[\begin{align*} \cos(2\theta)&= 2 {\cos}^2 \theta-1\\[4pt] 1+\cos(2\theta)&= 2 {\cos}^2 \theta\\[4pt] \dfrac{1+\cos(2\theta)}{2}&= {\cos}^2 \theta \end{align*}\]

The last reduction formula is derived by writing tangent in terms of sine and cosine:

\[\begin{align*} \tan^2 \theta &= \frac{\sin^2 \theta}{\cos^2 \theta} \\[4pt] &= \dfrac{\dfrac{1-\cos(2\theta)}{2}}{\dfrac{1+\cos(2\theta)}{2}} \qquad \tag{Substitute the reduction formulas} \\[4pt] &= \left(\dfrac{1-\cos(2 \theta)}{2}\right)\left(\dfrac{2}{1+\cos(2 \theta)}\right) \\[4pt] &= \dfrac{1-\cos(2 \theta)}{1+\cos(2 \theta)} \end{align*}\]

REDUCTION FORMULAS

The reduction formulas are summarized as follows:

\[{\sin}^2 \theta=\dfrac{1−\cos(2 \theta)}{2}\]

\[{\cos}^2 \theta=\dfrac{1+\cos(2 \theta)}{2}\]

\[{\tan}^2 \theta=\dfrac{1−\cos(2 \theta)}{1+\cos(2 \theta)}\]

Example \(\PageIndex{5}\): Writing an Equivalent Expression Not Containing Powers Greater Than 1

Write an equivalent expression for \({\cos}^4 x\) that does not involve any powers of sine or cosine greater than \(1\).

Solution

We will apply the reduction formula for cosine twice.

\[\begin{align*}
{\cos}^4 x&= {({\cos}^2 x)}^2\\[4pt]
&= {\left(\dfrac{1+\cos(2x)}{2}\right)}^2\qquad \text{Substitute reduction formula}\\[4pt]
&= \dfrac{1}{4}(1+2\cos(2x)+{\cos}^2 (2x))\\[4pt]
&= \dfrac{1}{4}+\dfrac{1}{2} \cos(2x)+\dfrac{1}{4}\left (\dfrac{1+{\cos}^2(2x)}{2}\right )\qquad \text{ Substitute reduction formula for } {\cos}^2 x\\[4pt]
&= \dfrac{1}{4}+\dfrac{1}{2} \cos(2x)+\dfrac{1}{8}+\dfrac{1}{8} \cos(4x)\\[4pt]
&= \dfrac{3}{8}+\dfrac{1}{2} \cos(2x)+\dfrac{1}{8} \cos(4x)
\end{align*}\]

Analysis

The solution is found by using the reduction formula twice, as noted, and the perfect square formula from algebra.

Using Half-Angle Formulas to Find Exact Values

The next set of identities is the set of half-angle formulas, which can be derived from the reduction formulas and we can use when we have an angle that is half the size of a special angle. If we replace \(\theta\) with \(\dfrac{\alpha}{2}\),the half-angle formula for sine is found by simplifying the equation and solving for \(\sin\left(\dfrac{\alpha}{2}\right)\). Note that the half-angle formulas are preceded by a \(\pm\) sign. This does not mean that both the positive and negative expressions are valid. Rather, it depends on the quadrant in which \(\dfrac{\alpha}{2}\) terminates.

The half-angle formula for sine is derived as follows:

\[\begin{align*} {\sin}^2 \theta&= \dfrac{1-\cos(2\theta)}{2}\\[4pt] {\sin}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\left(\cos 2\cdot \dfrac{\alpha}{2}\right)}{2}\\[4pt] &= \dfrac{1-\cos \alpha}{2}\\[4pt] \sin \left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}} \end{align*}\]

To derive the half-angle formula for cosine, we have

\[\begin{align*} {\cos}^2 \theta&= \dfrac{1+\cos(2\theta)}{2}\\[4pt] {\cos}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1+\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{2}\\[4pt] &= \dfrac{1+\cos \alpha}{2}\\[4pt] \cos\left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}} \end{align*}\]

For the tangent identity, we have

\[\begin{align*} {\tan}^2 \theta&= \dfrac{1-\cos(2\theta)}{1+\cos(2\theta)}\\[4pt] {\tan}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{1+\cos\left(2\cdot \dfrac{\alpha}{2}\right)}\\[4pt] \tan\left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} \end{align*}\]

HALF-ANGLE FORMULAS

The half-angle formulas are as follows:

\[\begin{align} \sin\left(\dfrac{\alpha}{2}\right)&=\pm \sqrt{\dfrac{1-\cos \alpha}{2}} \label{halfsine} \\[4pt] \cos \left(\dfrac{\alpha}{2} \right) &=\pm \sqrt{\dfrac{1+\cos \alpha}{2}} \\[4pt] \tan\left(\dfrac{\alpha}{2}\right) &=\pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} =\dfrac{\sin \alpha}{1+\cos \alpha} =\dfrac{1-\cos \alpha}{\sin \alpha}\end{align}\]

Example \(\PageIndex{7}\)

Using a Half-Angle Formula to Find the Exact Value of a Sine Function. Find \(\sin(15°)\) using a half-angle formula.

Solution

Since \(15°=\dfrac{30°}{2}\),we use the half-angle formula for sine (Equation \ref{halfsine}):

\[\begin{align*}
\sin \dfrac{30^{\circ}}{2}&= \sqrt{\dfrac{1-\cos 30^{\circ}}{2}}\\[4pt]
&= \sqrt{\dfrac{1-\dfrac{\sqrt{3}}{2}}{2}}\\[4pt]
&= \sqrt{\dfrac{\dfrac{2-\sqrt{3}}{2}}{2}}\\[4pt]
&= \sqrt{\dfrac{2-\sqrt{3}}{4}}\\[4pt]
&= \dfrac{\sqrt{2-\sqrt{3}}}{2}
\end{align*}\]

Remember that we can check the answer with a graphing calculator.

Analysis

Notice that we used only the positive root because \(\sin(15°)\) is positive.

Howto: Given the tangent of an angle and the quadrant in which the angle lies, find the exact values of trigonometric functions of half of the angle.

1. Draw a triangle to represent the given information.
2. Determine the correct half-angle formula.
3. Substitute values into the formula based on the triangle.
4. Simplify.

Example \(\PageIndex{8}\): Finding Exact Values Using Half-Angle Identities

Given that \(\tan \alpha=\dfrac{8}{15}\) and \(α\) lies in quadrant III, find the exact value of the following:

1. \(\sin\left(\dfrac{\alpha}{2}\right)\)
2. \(\cos\left(\dfrac{\alpha}{2}\right)\)
3. \(\tan\left(\dfrac{\alpha}{2}\right)\)

Solution

Using the given information, we can draw the triangle shown in Figure \(\PageIndex{3}\). Using the Pythagorean Theorem, we find the hypotenuse to be 17. Therefore, we can calculate \(\sin \alpha=−\dfrac{8}{17}\) and \(\cos \alpha=−\dfrac{15}{17}\).

Figure \(\PageIndex{3}\)

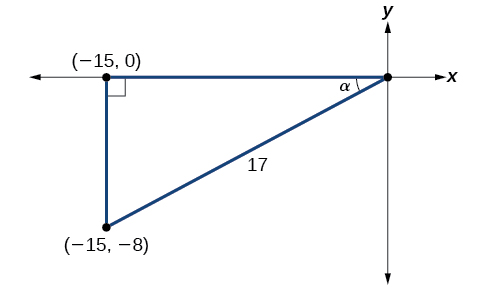
1. Before we start, we must remember that if \(α\) is in quadrant III, then \(180°<\alpha<270°\),so \(\dfrac{180°}{2}<\dfrac{\alpha}{2}<\dfrac{270°}{2}\). This means that the terminal side of \(\dfrac{\alpha}{2}\) is in quadrant II, since \(90°<\dfrac{\alpha}{2}<135°\). To find \(\sin \dfrac{\alpha}{2}\),we begin by writing the half-angle formula for sine. Then we substitute the value of the cosine we found from the triangle in Figure \(\PageIndex{3}\) and simplify. \[\begin{align*} \sin \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1-(-\dfrac{15}{17})}{2}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{2}}\\[4pt] &= \pm \sqrt{\dfrac{32}{17}\cdot \dfrac{1}{2}}\\[4pt] &= \pm \sqrt{\dfrac{16}{17}}\\[4pt] &= \pm \dfrac{4}{\sqrt{17}}\\[4pt] &= \dfrac{4\sqrt{17}}{17} \end{align*}\] We choose the positive value of \(\sin \dfrac{\alpha}{2}\) because the angle terminates in quadrant II and sine is positive in quadrant II.
2. To find \(\cos \dfrac{\alpha}{2}\),we will write the half-angle formula for cosine, substitute the value of the cosine we found from the triangle in Figure \(\PageIndex{3}\), and simplify. \[\begin{align*} \cos \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1+\left(-\dfrac{15}{17}\right)}{2}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{2}{17}}{2}}\\[4pt] &= \pm \sqrt{\dfrac{2}{17}\cdot \dfrac{1}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1}{17}}\\[4pt] &= -\dfrac{\sqrt{17}}{17} \end{align*}\] We choose the negative value of \(\cos \dfrac{\alpha}{2}\) because the angle is in quadrant II because cosine is negative in quadrant II.
3. To find \(\tan \dfrac{\alpha}{2}\),we write the half-angle formula for tangent. Again, we substitute the value of the cosine we found from the triangle in Figure \(\PageIndex{3}\) and simplify. \[\begin{align*} \tan \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}}\\[4pt] &= \pm \sqrt{\dfrac{1-\left(-\dfrac{15}{17}\right)}{1+\left(-\dfrac{15}{17}\right)}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{\dfrac{2}{17}}}\\[4pt] &= \pm \sqrt{\dfrac{32}{2}}\\[4pt] &= -\sqrt{16}\\[4pt] &= -4 \end{align*}\] We choose the negative value of \(\tan \dfrac{\alpha}{2}\) because \(\dfrac{\alpha}{2}\) lies in quadrant II, and tangent is negative in quadrant II.