8.1: Non-right Triangles - Law of Sines
- Page ID
- 117164
Using the Law of Sines to Solve Oblique Triangles
In any triangle, we can draw an altitude, a perpendicular line from one vertex to the opposite side, forming two right triangles. It would be preferable, however, to have methods that we can apply directly to non-right triangles without first having to create right triangles.
Any triangle that is not a right triangle is an oblique triangle. Solving an oblique triangle means finding the measurements of all three angles and all three sides. To do so, we need to start with at least three of these values, including at least one of the sides. We will investigate three possible oblique triangle problem situations:
ASA (angle-side-angle) We know the measurements of two angles and the included side. See Figure \(\PageIndex{2}\).
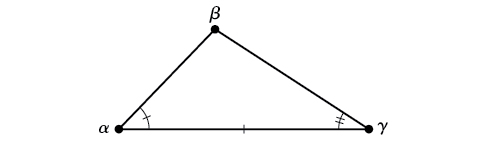
Figure \(\PageIndex{2}\)
AAS (angle-angle-side) We know the measurements of two angles and a side that is not between the known angles. See Figure \(\PageIndex{3}\).
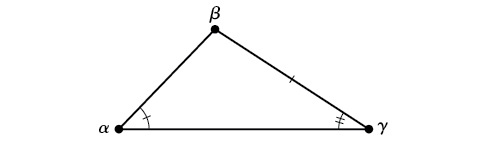
Figure \(\PageIndex{3}\)
SSA (side-side-angle) We know the measurements of two sides and an angle that is not between the known sides. See Figure \(\PageIndex{4}\).
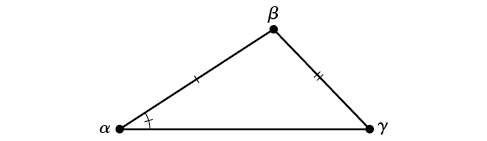
Figure \(\PageIndex{4}\)
Knowing how to approach each of these situations enables us to solve oblique triangles without having to drop a perpendicular to form two right triangles. Instead, we can use the fact that the ratio of the measurement of one of the angles to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. Let’s see how this statement is derived by considering the triangle shown in Figure \(\PageIndex{5}\).
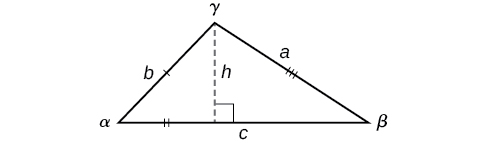
Figure \(\PageIndex{5}\)
Using the right triangle relationships, we know that \(\sin \alpha=\dfrac{h}{b}\) and \(\sin \beta=\dfrac{h}{a}\). Solving both equations for \(h\) gives two different expressions for \(h\).
\(h=b \sin \alpha\) and \(h=a \sin \beta\)
We then set the expressions equal to each other.
\[\begin{align*} b \sin \alpha&= a \sin \beta\\ \left(\dfrac{1}{ab}\right)\left(b \sin \alpha\right)&= \left(a \sin \beta\right)\left(\dfrac{1}{ab}\right)\qquad \text{Multiply both sides by } \dfrac{1}{ab}\\ \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b} \end{align*}\]
Similarly, we can compare the other ratios.
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \gamma}{c}\) and \(\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\)
Collectively, these relationships are called the Law of Sines.
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\)
Note the standard way of labeling triangles: angle \(\alpha\) (alpha) is opposite side \(a\); angle \(\beta\) (beta) is opposite side \(b\); and angle \(\gamma\) (gamma) is opposite side \(c\). See Figure \(\PageIndex{6}\).
While calculating angles and sides, be sure to carry the exact values through to the final answer. Generally, final answers are rounded to the nearest tenth, unless otherwise specified.
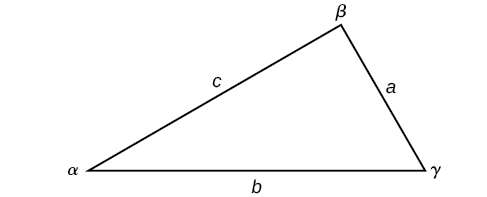
Figure \(\PageIndex{6}\)
Given a triangle with angles and opposite sides labeled as in Figure \(\PageIndex{6}\), the ratio of the measurement of an angle to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. All proportions will be equal. The Law of Sines is based on proportions and is presented symbolically two ways.
\[\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\]
\[\dfrac{a}{\sin \alpha}=\dfrac{b}{\sin \beta}=\dfrac{c}{\sin \gamma}\]
To solve an oblique triangle, use any pair of applicable ratios.
Solve the triangle shown in Figure \(\PageIndex{7}\) to the nearest tenth.
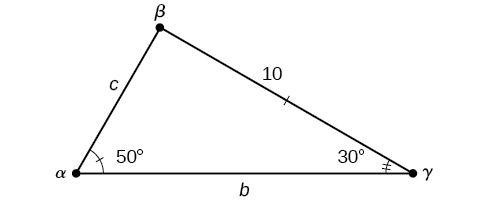
Figure \(\PageIndex{7}\)
Solution
The three angles must add up to 180 degrees. From this, we can determine that
\[\begin{align*} \beta &= 180^{\circ} - 50^{\circ} - 30^{\circ}\\ &= 100^{\circ} \end{align*}\]
To find an unknown side, we need to know the corresponding angle and a known ratio. We know that angle \(\alpha=50°\)and its corresponding side \(a=10\). We can use the following proportion from the Law of Sines to find the length of \(c\).
\[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(30^{\circ})}{c}\\ c\dfrac{\sin(50^{\circ})}{10}&= \sin(30^{\circ})\qquad \text{Multiply both sides by } c\\ c&= \sin(30^{\circ})\dfrac{10}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate } c\\ c&\approx 6.5 \end{align*}\]
Similarly, to solve for \(b\), we set up another proportion.
\[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(100^{\circ})}{b}\\ b \sin(50^{\circ})&= 10 \sin(100^{\circ})\qquad \text{Multiply both sides by } b\\ b&= \dfrac{10 \sin(100^{\circ})}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate }b\\ b&\approx 12.9 \end{align*}\]
Therefore, the complete set of angles and sides is
\(\begin{matrix} \alpha=50^{\circ} & a=10\\ \beta=100^{\circ} & b\approx 12.9\\ \gamma=30^{\circ} & c\approx 6.5 \end{matrix}\)
Finding the Area of an Oblique Triangle Using the Sine Function
Now that we can solve a triangle for missing values, we can use some of those values and the sine function to find the area of an oblique triangle. Recall that the area formula for a triangle is given as \(Area=\dfrac{1}{2}bh\), where \(b\) is base and \(h\) is height. For oblique triangles, we must find \(h\) before we can use the area formula. Observing the two triangles in Figure \(\PageIndex{15}\), one acute and one obtuse, we can drop a perpendicular to represent the height and then apply the trigonometric property \(\sin \alpha=\dfrac{opposite}{hypotenuse}\) to write an equation for area in oblique triangles. In the acute triangle, we have \(\sin \alpha=\dfrac{h}{c}\) or \(c \sin \alpha=h\). However, in the obtuse triangle, we drop the perpendicular outside the triangle and extend the base \(b\) to form a right triangle. The angle used in calculation is \(\alpha′\), or \(180−\alpha\).
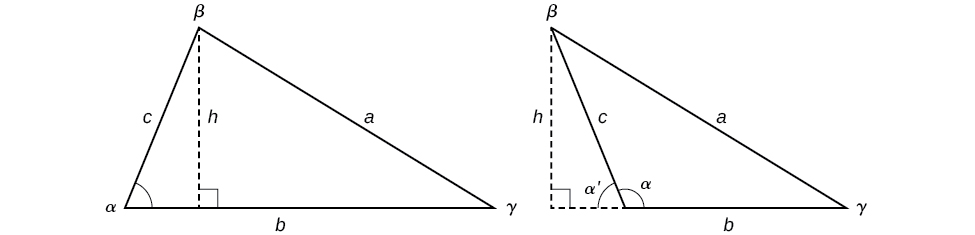
Figure \(\PageIndex{15}\)
Thus,
\(Area=\dfrac{1}{2}(base)(height)=\dfrac{1}{2}b(c \sin \alpha)\)
Similarly,
\(Area=\dfrac{1}{2}a(b \sin \gamma)=\dfrac{1}{2}a(c \sin \beta)\)
The formula for the area of an oblique triangle is given by
\[Area=\dfrac{1}{2}bc \sin \alpha\]
\[Area=\dfrac{1}{2}ac \sin \beta\]
\[Area=\dfrac{1}{2}ab \sin \gamma\]
This is equivalent to one-half of the product of two sides and the sine of their included angle.
Find the area of a triangle with sides \(a=90\), \(b=52\), and angle \(\gamma=102°\). Round the area to the nearest integer.
Solution
Using the formula, we have
\[\begin{align*} Area&= \dfrac{1}{2}ab \sin \gamma\\ Area&= \dfrac{1}{2}(90)(52) \sin(102^{\circ})\\ Area&\approx 2289\; \text{square units} \end{align*}\]


