8.2: Non-right Triangles - Law of Cosines

Using the Law of Cosines to Solve Oblique Triangles

The tool we need to solve the problem of the boat’s distance from the port is the Law of Cosines, which defines the relationship among angle measurements and side lengths in oblique triangles. Three formulas make up the Law of Cosines. At first glance, the formulas may appear complicated because they include many variables. However, once the pattern is understood, the Law of Cosines is easier to work with than most formulas at this mathematical level.

Understanding how the Law of Cosines is derived will be helpful in using the formulas. The derivation begins with the Generalized Pythagorean Theorem, which is an extension of the Pythagorean Theorem to non-right triangles. Here is how it works: An arbitrary non-right triangle \(ABC\) is placed in the coordinate plane with vertex \(A\) at the origin, side \(c\) drawn along the x-axis, and vertex \(C\) located at some point \((x,y)\) in the plane, as illustrated in Figure \(\PageIndex{2}\). Generally, triangles exist anywhere in the plane, but for this explanation we will place the triangle as noted.

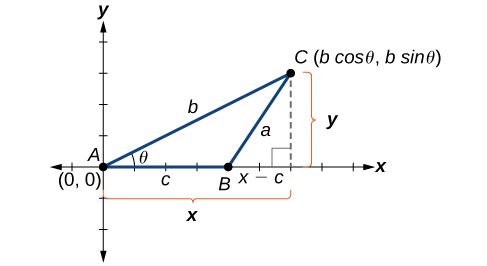
Figure \(\PageIndex{2}\)

We can drop a perpendicular from \(C\) to the x-axis (this is the altitude or height). Recalling the basic trigonometric identities, we know that

\(\cos \theta=\dfrac{x(adjacent)}{b(hypotenuse)}\) and \(\sin \theta=\dfrac{y(opposite)}{b(hypotenuse)}\)

In terms of \(\theta\), \(x=b \cos \theta\) and \(y=b \sin \theta\). The \((x,y)\) point located at \(C\) has coordinates \((b \cos \theta, b \sin \theta)\). Using the side \((x−c)\) as one leg of a right triangle and \(y\) as the second leg, we can find the length of hypotenuse \(a\) using the Pythagorean Theorem. Thus,

\(\begin{array}{ll} a^2={(x−c)}^2+y^2 \\[4pt] \;\;\;\;\; ={(b \cos \theta−c)}^2+{(b \sin \theta)}^2 & \text{Substitute }(b \cos \theta) \text{ for }x \text{ and }(b \sin \theta)\text{ for }y \\[4pt] \;\;\;\;\;\; =(b^2{\cos}^2 \theta−2bc \cos \theta+c^2)+b^2 {\sin}^2 \theta & \text{Expand the perfect square.} \\[4pt] \;\;\;\;\; =b^2{\cos}^2 \theta+b^2{\sin}^2 \theta+c^2−2bc \cos \theta & \text{Group terms noting that }{\cos}^2 \theta+{\sin}^2 \theta=1 \\[4pt] \;\;\;\;\; =b^2({\cos}^2 \theta+{\sin}^2 \theta)+c^2−2bc \cos \theta & \text{Factor out }b^2 \\[4pt]
a^2=b^2+c^2−2bc \cos \theta \end{array}\)

The formula derived is one of the three equations of the Law of Cosines. The other equations are found in a similar fashion.

Keep in mind that it is always helpful to sketch the triangle when solving for angles or sides. In a real-world scenario, try to draw a diagram of the situation. As more information emerges, the diagram may have to be altered. Make those alterations to the diagram and, in the end, the problem will be easier to solve.

The LAW OF COSINES

The Law of Cosines states that the square of any side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of the other two sides and the cosine of the included angle.

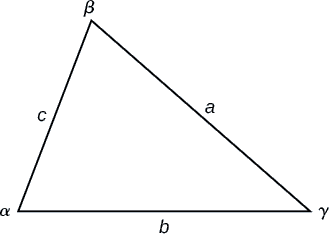
Figure \(\PageIndex{3}\)

For triangles labeled as in Figure \(\PageIndex{3}\), with angles \(\alpha\), \(\beta\) and \(\gamma\), and opposite corresponding sides \(a\), \(b\), and \(c\), respectively, the Law of Cosines is given as three equations.

\[a^2=b^2+c^2−2bc \cos \alpha\]

\[b^2=a^2+c^2−2ac \cos \beta\]

\[c^2=a^2+b^2−2ab \cos \gamma\]

To solve for a missing side measurement, the corresponding opposite angle measure is needed.

When solving for an angle, the corresponding opposite side measure is needed. We can use another version of the Law of Cosines to solve for an angle.

\[\cos \alpha=\dfrac{b^2+c^2−a^2}{2bc}\]

\[\cos \beta=\dfrac{a^2+c^2−b^2}{2ac}\]

\[\cos \gamma=\dfrac{a^2+b^2−c^2}{2ab}\]

How to: Given two sides and the angle between them (SAS), find the measures of the remaining side and angles of a triangle

1. Sketch the triangle. Identify the measures of the known sides and angles. Use variables to represent the measures of the unknown sides and angles.
2. Apply the Law of Cosines to find the length of the unknown side or angle.
3. Apply the Law of Sines or Cosines to find the measure of a second angle.
4. Compute the measure of the remaining angle.

Example \(\PageIndex{1}\): Finding the Unknown Side and Angles of a SAS Triangle

Find the unknown side and angles of the triangle in Figure \(\PageIndex{4}\).

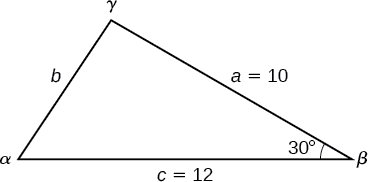
Figure \(\PageIndex{4}\)

Solution

First, make note of what is given: two sides and the angle between them. This arrangement is classified as SAS and supplies the data needed to apply the Law of Cosines.

Each one of the three laws of cosines begins with the square of an unknown side opposite a known angle. For this example, the first side to solve for is side \(b\), as we know the measurement of the opposite angle \(\beta\).

\(\begin{array}{ll} b^2=a^2+c^2−2ac \cos \beta \\[4pt] b^2={10}^2+{12}^2−2(10)(12)\cos(30°) & \text{Substitute the measurements for the known quantities.} \\[4pt] b^2=100+144−240 \left(\dfrac{\sqrt{3}}{2}\right) & \text{Evaluate the cosine and begin to simplify.} \\[4pt] b^2=244−120\sqrt{3} \\[4pt] b=\sqrt{244−120\sqrt{3}} & \text{Use the square root property.} \\[4pt] b≈6.013 \end{array}\)

Because we are solving for a length, we use only the positive square root. Now that we know the length \(b\), we can use the Law of Sines to fill in the remaining angles of the triangle. Solving for angle \(\alpha\), we have

\(\begin{array}{cc} \dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b} \\[4pt] \dfrac{\sin \alpha}{10}=\dfrac{\sin(30°)}{6.013} \\[4pt] \sin \alpha=\dfrac{10\sin(30°)}{6.013} & \text{Multiply both sides of the equation by }10. \\[4pt] \alpha={\sin}^{−1}\left(\dfrac{10\sin(30°)}{6.013}\right) & \text{Find the inverse sine of } \dfrac{10\sin(30°)}{6.013}. \\[4pt] \alpha≈56.3° \end{array}\)

The other possibility for \(\alpha\) would be \(\alpha=180°-56.3°≈123.7°\). In the original diagram,\(\alpha\) is adjacent to the longest side, so \(\alpha\) is an acute angle and, therefore, \(123.7°\) does not make sense. Notice that if we choose to apply the Law of Cosines, we arrive at a unique answer. We do not have to consider the other possibilities, as cosine is unique for angles between \(0°\) and \(180°\). Proceeding with \(\alpha≈56.3°\), we can then find the third angle of the triangle.

\[\begin{align*} \gamma&= 180^{\circ}-30^{\circ}-56.3^{\circ}\\ &\approx 93.7^{\circ} \end{align*}\]

The complete set of angles and sides is

\(\alpha≈56.3°\) \(a=10\)

\(\beta=30°\) \(b≈6.013\)

\(\gamma≈93.7°\) \(c=12\)

Using Heron’s Formula to Find the Area of a Triangle

We already learned how to find the area of an oblique triangle when we know two sides and an angle. We also know the formula to find the area of a triangle using the base and the height. When we know the three sides, however, we can use Heron’s formula instead of finding the height. Heron of Alexandria was a geometer who lived during the first century A.D. He discovered a formula for finding the area of oblique triangles when three sides are known.

HERON’S FORMULA

Heron’s formula finds the area of oblique triangles in which sides \(a\), \(b\),and \(c\) are known.

\[Area=\sqrt{s(s−a)(s−b)(s−c)}\]

where \(s=\dfrac{(a+b+c)}{2}\) is one half of the perimeter of the triangle, sometimes called the semi-perimeter.

Example \(\PageIndex{4}\): Using Heron’s Formula to Find the Area of a Given Triangle

Find the area of the triangle in Figure \(\PageIndex{9}\) using Heron’s formula.

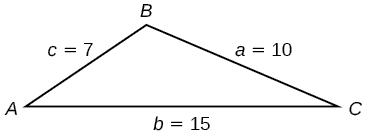
Figure \(\PageIndex{9}\)

Solution

First, we calculate \(s\).

\[\begin{align*} s&= \dfrac{(a+b+c)}{2}\\ s&= \dfrac{(10+15+7)}{2}\\ &= 16 \end{align*}\]

Then we apply the formula.

\[\begin{align*} Area&= \sqrt{s(s-a)(s-b)(s-c)}\\ Area&= \sqrt{16(16-10)(16-15)(16-7)}\\ Area&\approx 29.4 \end{align*}\]

The area is approximately \(29.4\) square units.