3.1.1: Union, Intersection, and Complement

 

3.1.1 Learning Objectives

•  Find the union and intersection of two sets

•  Find the complement of a set relative to a universal set

•  Use and interpret set notation for unions, intersections and complements of sets

Commonly sets interact. For example, you and a new roommate decide to have a house party, and you both invite your circle of friends. At this party, two sets are being combined, though it might turn out that there are some friends that were in both sets.

Definition: Union, Intersection, and Complement

The union of two sets contains all the elements contained in either set (or both sets). The word that you will often see that indicates a union is "or".

The union is notated $A \cup B$

More formally, $x \in A \cup B$ if $x \in A$ or $x \in B$ (or both)

The intersection of two sets contains only the elements that are in both sets. The word that you will often see that indicates an intersection is "and".

The intersection is notated $A \cap B$

More formally, $x \in A \cap B$ if $x \in A$ and $x \in B$

The complement of a set A contains everything that is not in the set A.

The complement is notated $A$, or $A^{c}$, or sometimes $\sim A$.Example $\PageIndex{1}$

Example 1

Consider the sets:

$\quad A=\{\text { red, green, blue }\} \quad B=\{\text { red, yellow, orange }\} \quad C=\{\text { red, orange, yellow, green, blue, purple }\}$

1. Find $A \cup B$ (Hint: This means the union of two sets, so it means elements could belong to set A, set B, or both sets, commonly referred as A or B)
2. Find $A \cap B$ (Hint: This means the intersection of two sets, so it means elements must be in common in both sets, commonly referred as A and B)
3. Find $A^{c} \cap C$

Solution

A Venn diagram can help organize each of these problems. 

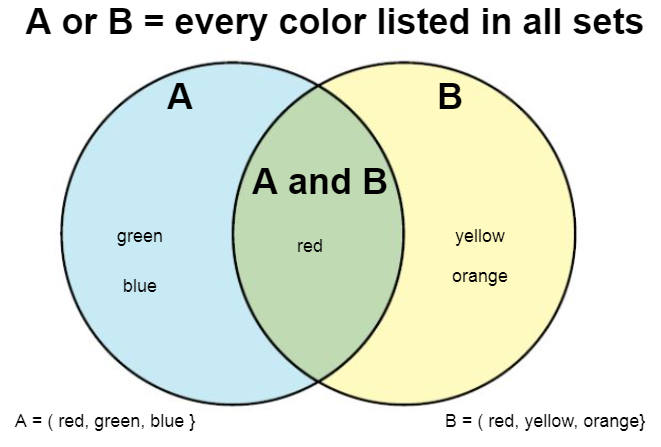
a) The union contains all the elements in either set: $A \cup B=\{\text { red, green, blue, yellow, orange }\}$

Notice we only list red once.

b) The intersection contains all the elements in both sets: $A \cap B=\{\text { red }\}$

c) Here we're looking for all the elements that are not in set $A$ and are also in $C$.

$A^{c} \cap C=\{\text { orange, yellow, purple }\}$

Try it Now 1

Using the sets from the previous example, find $A \cup C$ and $B^{c} \cap A$

Answer

$A \cup C=\{\text { red, orange, yellow, green, blue purple }\}$

$B^{c} \cap A=\{\text { green, blue }\}$

Notice that in the example above, it would be hard to just ask for $A^{c},$ since everything from the color fuchsia to puppies and peanut butter are included in the complement of the set. For this reason, complements are usually only used with intersections, or when we have a universal set in place.

Definition: Universal Set

A universal set is a set that contains all the elements we are interested in. This would have to be defined by the context.

A complement is relative to the universal set, so $A^{C}$ contains all the elements in the universal set that are not in $A$.

Example 2

1. If we were discussing searching for books, the universal set might be all the books in the library.
2. If we were grouping your Facebook friends, the universal set would be all your Facebook friends.
3. If you were working with sets of numbers, the universal set might be all whole numbers, all integers, or all real numbers

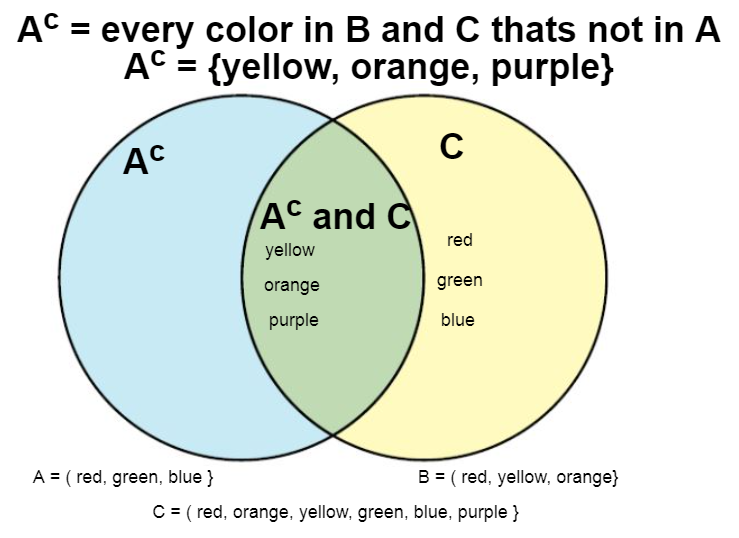
Example 3

Suppose the universal set is $U=$ all whole numbers from $1$ to $9 .$ If $A=\{1,2,4\}$, then

$A^{c}=\{3,5,6,7,8,9\}$

As we saw earlier with the expression $A^{c} \cap C,$ set operations can be grouped together. Grouping symbols can be used like they are with arithmetic - to force an order of operations.

Example 4

Suppose

$H=\{\text { cat, dog, rabbit, mouse }\}, F=\{\text { dog, cow, duck, pig, rabbit }\} \quad W=\{\text { duck, rabbit, deer, frog, mouse }\}$

1. Find $(H \cap P) \cup W$
2. Find $H \cap(F \cup W)$
3. Find $(H \cap P) \cap W$

Solution

a) We start with the intersection: $H \cap F=\{\text { dog, rabbit }\}$

Now we union that result with $W:(H \cap F) \cup W=\{\text{dog, duck, rabbit, deer, frog, mouse }\}$

b) We start with the union: $F \cup W=\{\text{dog, cow, rabbit, duck, pig, deer, frog, mouse }\}$

Now we intersect that result with $H: H \cap(F \cup W)=\{\text { dog, rabbit, mouse }\}$

c) We start with the intersection: $H \cap F=\{\mathrm{dog}, \text { rabbit }\}$

Now we want to find the elements of $W$ that are not in $\mathrm{H} \cap F$

$(H \cap P)^{c} \cap W=\{\text { duck, deer, frog, mouse }\}$