2.2: Applications of Radian Measure

Learning Objectives

• Solve problems involving angles of rotation using radian measure.
• Calculate the length of an arc and the area of a sector.
• Approximate the length of a chord given the central angle and radius.
• Solve problems about angular speed.

In Section 2.1 we saw that one revolution has a radian measure of \(2\pi \) rad. Note that \(2\pi\) is the ratio of the circumference (i.e. total arc length) \(C \) of a circle to its radius \(r\):
\[\nonumber
\text{Radian measure of 1 revolution} ~=~ 2\pi ~=~ \frac{2\pi\,r}{r} ~=~
\frac{C}{r} ~=~ \frac{\text{total arc length}}{\text{radius}}
\]
Clearly, that ratio is independent of \(r \). In general, the radian measure of an angle is the ratio of the arc length cut off by the corresponding central angle in a circle to the radius of the circle, independent of the radius.

Figure 2.2.1 Radian measure and arc length

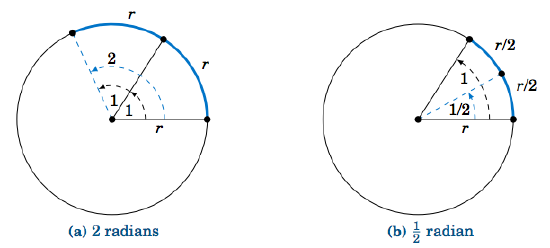
Now suppose that we cut the angle with radian measure \(1 \) in half, as in Figure 2.2.1(b). Clearly, this cuts the arc length \(r \) in half as well. Thus, we see that
\[\nonumber \begin{align}
\text{Angle} ~&=~ 1~\text{radian} \quad&\Rightarrow\quad \text{arc length} ~&=~ r ~,\\ \nonumber
\text{Angle} ~&=~ 2~\text{radians} \quad&\Rightarrow\quad \text{arc length} ~&=~ 2\,r ~,\\ \nonumber
\text{Angle} ~&=~ \tfrac{1}{2}~\text{radian} \quad&\Rightarrow\quad \text{arc length} ~&=~
\tfrac{1}{2}\,r ~,\end{align}\]
and in general, for any \(\theta \ge 0 \),
\[\nonumber \text{Angle} ~=~ \theta~\text{radians} \quad \Rightarrow\quad \text{arc length} ~=~ \theta\,r ~,
\]
so that
\[\nonumber
\theta ~=~ \frac{\text{arc length}}{\text{radius}} ~~.
\]

Intuitively, it is obvious that shrinking or magnifying a circle preserves the measure of a central angle even as the radius changes. The above discussion says more, namely that the ratio of the length \(s \) of an intercepted arc to the radius \(r \) is preserved, precisely because that ratio is the measure of the central angle in radians (see Figure 2.2.2).

Figure 2.2.2 Circles with the same central angle, different radii

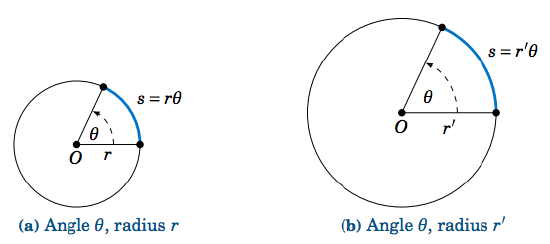
We thus get a simple formula for the length of an arc:

In a circle of radius \(r \), let \(s \) be the length of an arc intercepted by a central angle with radian measure \(\theta \ge 0 \). Then the arc length \(s \) is:

\[ s ~=~ r\,\theta \label{4.4}\]

Example \(\PageIndex{1}\)

Find the arc length of a circle with a radius of 10 feet and a central angle of \(41^\circ \).

Solution

So first convert \(\theta =41^\circ \) to radians, then use \(s=r\,\theta\):

\[\theta = 41^\circ ~=~ \frac{\pi}{180} \;\cdot\; 41 ~=~ 0.716~\text{rad}
\quad\Rightarrow\quad s ~=~ r\,\theta ~=~ (10)\,(0.716) ~=~ \boxed{7.16~\text{ft}}\nonumber\]

Note that since the arc length \(s \) and radius \(r \) are usually given in the same units, radian measure is really unitless, since you can think of the units canceling in the ratio \(\frac{s}{r} \), which is just \(\theta \). This is another reason why radians are so widely used.

For central angles \(\theta > 2\pi \) rad, i.e. \(\theta > 360^\circ \), it may not be clear what is meant by the intercepted arc, since the angle is larger than one revolution and hence "wraps around'' the circle more than once. We will take the approach that such an arc consists of the full circumference plus any additional arc length determined by the angle. In other words, Equation \ref{4.4} is still valid for angles \(\theta > 2\pi \) rad.

What about negative angles? In this case using \(s=r\,\theta \) would mean that the arc length is negative, which violates the usual concept of length. So we will adopt the convention of only using nonnegative central angles when discussing arc length.

Example \(\PageIndex{2}\)

A rope is fastened to a wall in two places \(8 \) ft apart at the same height. A cylindrical container with a radius of \(2 \) ft is pushed away from the wall as far as it can go while being held in by the rope, as in Figure 2.2.3 which shows the top view. If the center of the container is \(3 \) feet away from the point on the wall midway between the ends of the rope, what is the length \(L \) of the rope?

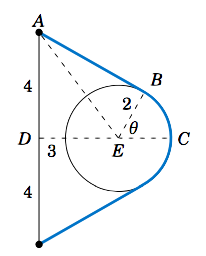
Figure 2.2.3

Solution

We see that, by symmetry, the total length of the rope is \(\;L = 2\;(AB + \overparen{BC}) \). Also, notice that \(\triangle\,ADE \) is a right triangle, so the hypotenuse has length \(AE = \sqrt{DE^2 + DA^2} = \sqrt{3^2 + 4^2} = 5 \) ft, by the Pythagorean Theorem. Now since \(\overline{AB} \) is tangent to the circular container, we know that \(\angle\,ABE \) is a right angle. So by the Pythagorean Theorem we have

\[ AB ~=~ \sqrt{AE^2 - BE^2} ~=~ \sqrt{5^2 - 2^2} ~=~ \sqrt{21} ~\text{ft}. \nonumber \]

By Equation \ref{4.4} the arc \(\overparen{BC} \) has length \(BE \cdot \theta \), where \(\theta = \angle\,BEC \) is the supplement of \(\angle\,AED + \angle\,AEB \). So since

\[\nonumber
\tan\,\angle\,AED ~=~ \frac{4}{3} ~\Rightarrow~ \angle\,AED ~=~ 53.1^\circ \quad\text{and}\quad
\cos\,\angle\,AEB ~=~ \frac{BE}{AE} ~=~ \frac{2}{5} ~\Rightarrow~ \angle\,AEB ~=~ 66.4^\circ ~,
\]

we have

\[ \nonumber
\theta ~=~ \angle\,BEC ~=~ 180^\circ \;-\; (\angle\,AED + \angle\,AEB) ~=~ 180^\circ \;-\;
(53.1^\circ + 66.4^\circ) ~=~ 60.5^\circ ~.
\]

Converting to radians, we get \(\;\theta = \frac{\pi}{180} \;\cdot\; 60.5 = 1.06 \) rad. Thus,

\[\nonumber
L ~=~ 2\,(AB \;+\; \cdot \overparen{BC}) ~=~ 2\,(\sqrt{21} \;+\; BE \cdot \theta) ~=~
2\,(\sqrt{21} \;+\; (2)\,( 1.06)) ~=~ \boxed{13.4 ~\text{ft}} ~.
\]

Area of a Sector

In geometry you learned that the area of a circle of radius \(r \) is \(\pi r^2 \). We will now learn how to find the area of a sector of a circle. A sector is the region bounded by a central angle and its intercepted arc, such as the shaded region in Figure 2.2.1.

Let \(\theta \) be a central angle in a circle of radius \(r \) and let \(A \) be the area of its sector. Similar to arc length, the ratio of \(A \) to the area of the entire circle is the same as the ratio of \(\theta \) to one revolution. In other words, again using radian measure,
\[\nonumber
\frac{\text{area of sector}}{\text{area of entire circle}} ~=~
\frac{\text{sector angle}}{\text{one revolution}} \quad\Rightarrow\quad
\frac{A}{\pi\,r^2} ~=~ \frac{\theta}{2\pi} ~.
\]
Solving for \(A \) in the above equation, we get the following formula:

In a circle of radius \(r \), the area \(A \) of the sector inside a central angle \(\theta \) is

\[ A ~=~ \tfrac{1}{2}\,r^2 \;\theta ~,\label{eqn:sectorarea}\]

where \(\theta \) is measured in radians.

Example \(\PageIndex{3}\)

Find the area of a sector whose angle is \(117^\circ \) in a circle of radius \(3.5 \) m.

Solution

As with arc length, we have to make sure that the angle is measured in radians or else the answer will be way off. So converting \(\theta=117^\circ \) to radians and using \(r=3.5 \) in Equation \ref{eqn:sectorarea} for the area \(A \) of the sector, we get
\[\nonumber
\theta ~=~ 117^\circ ~=~ \frac{\pi}{180} \;\cdot\; 117 ~=~ 2.042~\text{rad}
\quad\Rightarrow\quad
A ~=~ \tfrac{1}{2}\,r^2 \;\theta ~= \tfrac{1}{2}\,(3.5)^2 \;(2.042)
~=~ \boxed{12.51~\text{m}^2} ~.
\]

For a sector whose angle is \(\theta \) in a circle of radius \(r \), the length of the arc cut off by that angle is \(s=r\,\theta \). Thus, by Equation \ref{eqn:sectorarea} the area \(A \) of the sector can be written as:
\[
\boxed{ A ~=~ \tfrac{1}{2}\,rs}\label{eqn:sectorarc}
\]
Note: The central angle \(\theta \) that intercepts an arc is sometimes called the angle subtended by the arc.

Example \(\PageIndex{4}\)

Find the area of the sector of a circle with a radius of 6 and an arc length of 9.

Solution

Using \(s=6 \) and \(r=9 \) in Equation \ref{eqn:sectorarc} for the area \(A \), we get
\[\nonumber
A ~=~ \tfrac{1}{2}\,rs ~=~ ~=~ \tfrac{1}{2}\,(9)\,(6) ~=~ \boxed{27~\text{cm}^2} ~.
\]
Note that the angle subtended by the arc is \(\theta = \frac{s}{r} = \frac{2}{3} \) rad.

Linear and Angular Speed

Radian measure and arc length can be applied to the study of circular motion. In physics the average speed of an object is defined as:
\[\nonumber
\text{average speed} ~=~ \frac{\text{distance traveled}}{\text{time elapsed}}
\]

Figure 2.2.4

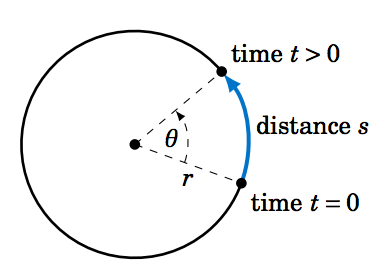
So suppose that an object moves along a circle of radius \(r \), traveling a distance \(s \) over a period of time \(t \), as in Figure 4.4.1. Then it makes sense to define the (average) linear speed \(\nu \) of the object as:

\[ \nu ~=~ \frac{s}{t}\label{eqn:linspeed}\]

Let \(\theta \) be the angle swept out by the object in that period of time. Then we define the (average) angular speed \(\omega \) of the object as:

\[ \omega ~=~ \frac{\theta}{t}\label{eqn:angspeed}\]

Angular speed gives the rate at which the central angle swept out by the object changes as the object moves around the circle, and it is thus measured in radians per unit time. Linear speed is measured in distance units per unit time (e.g. feet per second). The word linear is used because straightening out the arc traveled by the object along the circle results in a line of the same length, so that the usual definition of speed as distance over time can be used. We will usually omit the word average when discussing linear and angular speed here.

Since the length \(s \) of the arc cut off by a central angle \(\theta \) in a circle of radius \(r \) is \(s=r\,\theta \), we see that
\[\nonumber
\nu ~=~ \frac{s}{t} ~=~ \frac{r\,\theta}{t} ~=~ \frac{\theta}{t} \;\cdot\; r ~,
\]
so that we get the following relation between linear and angular speed:

\[ \nu ~=~ \omega\,r\label{eqn:linang}\]

Example \(\PageIndex{5}\)

An object sweeps out a central angle of \(\frac{\pi}{3} \) radians in \(0.5 \) seconds as it moves along a circle of radius \(3 \) m. Find its linear and angular speed over that time period.

Solution:

Here we have \(t=0.5 \) sec, \(r=3 \) m, and \(\theta = \frac{\pi}{3} \) rad. So the angular speed \(\omega \) is
\[\nonumber
\omega ~=~ \frac{\theta}{t} ~=~ \frac{\dfrac{\pi}{3}~\text{rad}}{0.5~\text{sec}}
\quad\Rightarrow\quad \boxed{\omega ~=~ \frac{2\pi}{3}~\text{rad/sec}} ~,
\]
and thus the linear speed \(\nu \) is
\[\nonumber
\nu ~=~ \omega\,r ~=~ \left( \frac{2\pi}{3}~\text{rad/sec} \right) \,(3~\text{m})
\quad\Rightarrow\quad \boxed{\nu ~=~ 2\pi~\text{m/sec}} ~.
\] Note that the units for \(\omega \) are rad/sec and the units of \(\nu \) are m/sec. Recall that radians are actually unitless, which is why in the Equation \(\nu=\omega\,r \) the radian units disappear.

Example \(\PageIndex{6}\)

An object travels a distance of \(35 \) ft in \(2.7 \) seconds as it moves along a circle of radius \(2 \) ft. Find its linear and angular speed over that time period.

Solution:

Here we have \(t=2.7 \) sec, \(r=2 \) ft, and \(s=35 \) ft. So the linear speed \(\nu \) is
\[\nonumber
\nu ~=~ \frac{s}{t} ~=~ \frac{35~\text{feet}}{2.7~\text{sec}} \quad\Rightarrow\quad
\boxed{\nu ~=~ 12.96~\text{ft/sec}} ~,
\]
and thus the angular speed \(\omega \) is given by
\[ \nonumber
\nu ~=~ \omega\,r \quad\Rightarrow\quad 12.96~\text{ft/sec} ~=~ \omega\,(2~\text{ft})
\quad\Rightarrow\quad \boxed{\omega ~=~ 6.48~\text{rad/sec}} ~.
\]

Example \(\PageIndex{7}\)

An object moves at a constant linear speed of \(10 \) m/sec around a circle of radius \(4 \) m. How large of a central angle does it sweep out in \(3.1 \) seconds?

Solution:

Here we have \(t=3.1 \) sec, \(\nu=10 \) m/sec, and \(r=4 \) m. Thus, the angle \(\theta \) is given by
\[\nonumber
s ~=~ r\,\theta \quad\Rightarrow\quad \theta ~=~ \frac{s}{r} ~=~ \frac{\nu\,t}{r} ~=~
\frac{(10~\text{m/sec})\,(3.1~\text{sec})}{4~\text{m}} ~=~ \boxed{7.75~\text{rad}} ~.
\]

In many physical applications angular speed is given in revolutions per minute, abbreviated as rpm. To convert from rpm to, say, radians per second, notice that since there are \(2\pi \) radians in one revolution and \(60 \) seconds in one minute, we can convert \(N \) rpm to radians per second by "canceling the units'' as follows:
\[\require{cancel} \nonumber
N~\text{rpm} ~=~ N~\frac{\cancel{\text{rev}}}{\cancel{\text{min}}} \;\cdot\;
\frac{2\pi~\text{rad}}{1~\cancel{\text{rev}}}
\;\cdot\; \frac{1~\cancel{\text{min}}}{60~\text{sec}} ~=~ \frac{N \cdot 2\pi}{60}~\text{rad/sec}
\]

Contributors and Attributions

• Michael Corral (Schoolcraft College). The content of this page is distributed under the terms of the GNU Free Documentation License, Version 1.2.